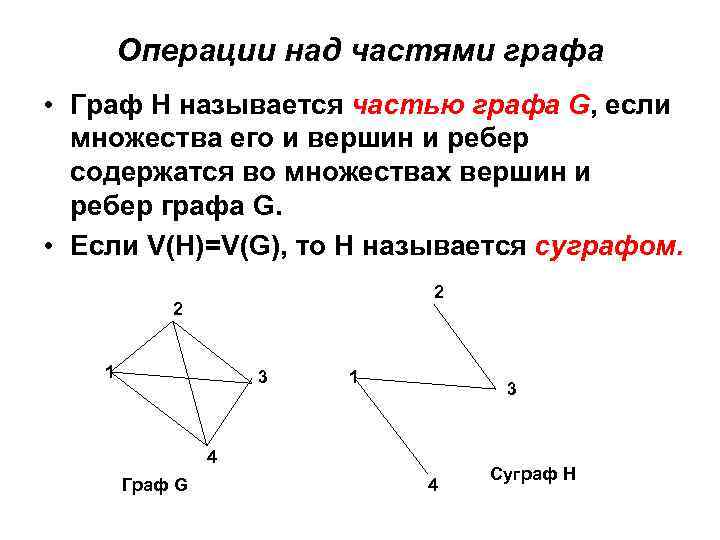
Операции над частями графа Граф Н называется

Операции над частями графа • Граф Н называется частью графа G, если множества его и вершин и ребер содержатся во множествах вершин и ребер графа G. • Если V(H)=V(G), то Н называется суграфом. 2 2 1 3 4 Граф G 4 Суграф Н

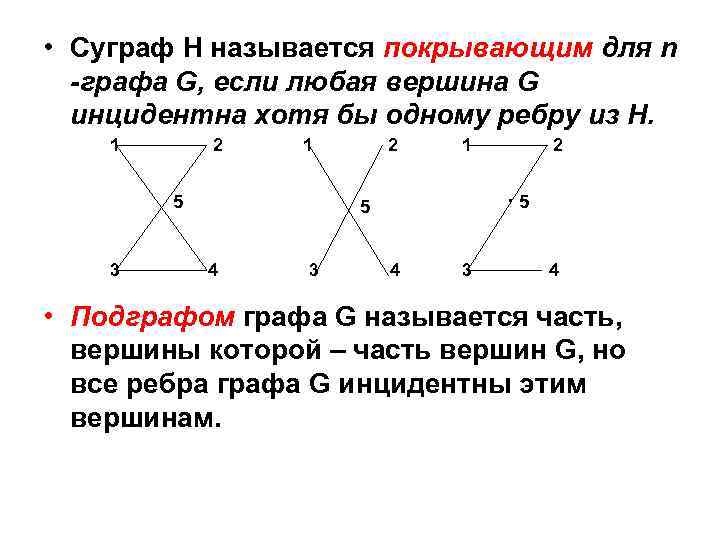• Суграф Н называется покрывающим для n -графа G, если любая вершина G инцидентна хотя бы одному ребру из Н. 1 2 1 5 3 2 1 . 5 5 4 3 2 4 3 4 • Подграфом графа G называется часть, вершины которой – часть вершин G, но все ребра графа G инцидентны этим вершинам.

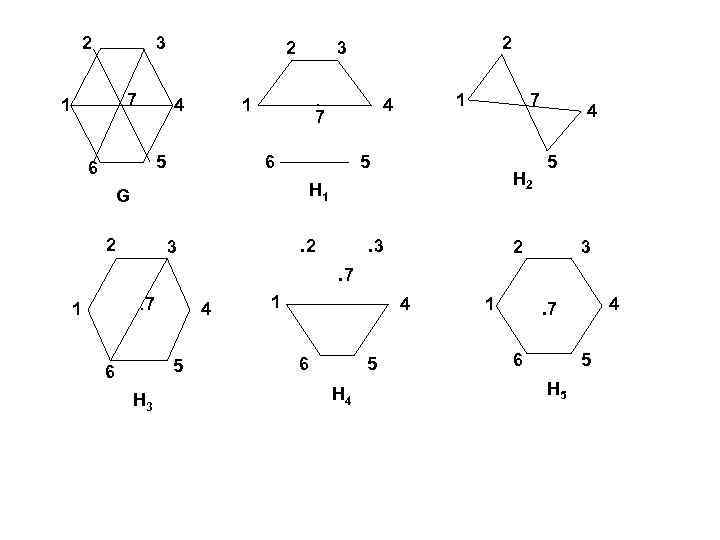2 3 7 1 2 4 . 1 5 6 2 3 1 4 7 6 7 5 Н 2 Н 1 G 2 . 2 3 . 3 4 5 2 3 . 7. 7 1 4 5 6 Н 3 1 4 6 5 Н 4 . 7 1 6 4 5 Н 5

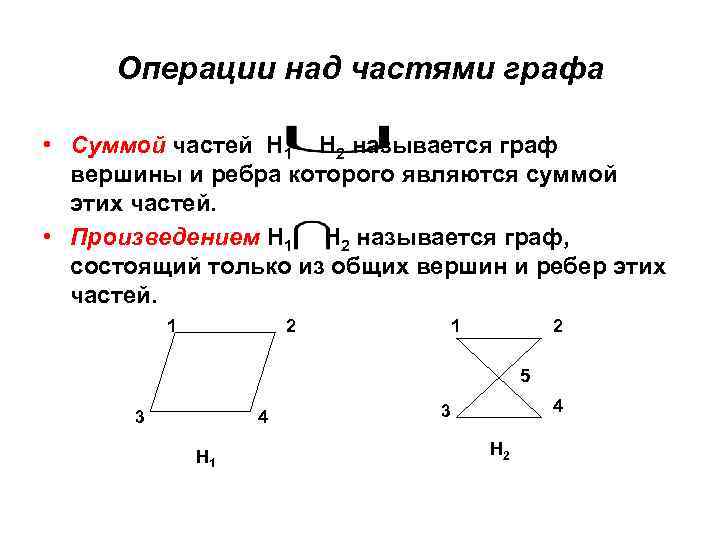Операции над частями графа • Суммой частей Н 1 Н 2 называется граф вершины и ребра которого являются суммой этих частей. • Произведением Н 1 Н 2 называется граф, состоящий только из общих вершин и ребер этих частей. 1 2 5 3 4 Н 1 4 3 Н 2

• Если V(H 1) V(H 2)= Ø, то сумма называется прямой. • Отношению R, заданному на множестве вершин графа взаимно-однозначно соответствует орграф без кратных ребер со множеством вершин V, в котором ребро (v 1; v 2) существует, если v 1 Rv 2

Свойства ор-графа, взаимно-однозначно соответствующего бинарному отношению R • • • R – рефлексивно R - антирефлексивно R – симметрично R – антисимметрично R - транзитивно • • • Граф – Граф –

Задание: Построить граф и определить свойства G 1 1 2 3 4 5 1 0 0 1 2 1 1 1 3 0 1 0 0 0 4 1 0 1 1 0 5 0 0 1 1 0

Задание: Построить граф, имеющий 5 вершин и обладающий свойствами: 1. 2. 3. Рефлексивен; симметричен. Не рефлексивен; не антирефлексивен; не симметричен; не антисимметричен. Антирефлексивен, антисимметричен.

Выполните задания По рис. 1 построить: • Суграф • Покрывающий суграф • Подграф По рис. 2 определить свойства графа По рис. 3(а) и 3(б) построить ор-графы