Open Source Model Checking Radu Grosu SUNY at

Open Source Model Checking Radu Grosu SUNY at Stony Brook Joint work with X. Huang, S. Jain and S. A. Smolka

GCC Compiler • Early stages: A modest C compiler. - Translation: source code translated directly to RTL. - Optimization: at low RTL level. - High level information lost: calls, structures, fields, etc. • Now days: Full blown, multi-language compiler generating code for more than 30 architectures. - Input: C, C++, Objective-C, Fortran, Java and Ada. - Tree-SSA: added GENERIC, GIMPLE and SSA ILs. - Optimization: at GENERIC, GIMPLE, SSA and RTL levels. - Verification: Tree-SSA API suitable for verification, too.

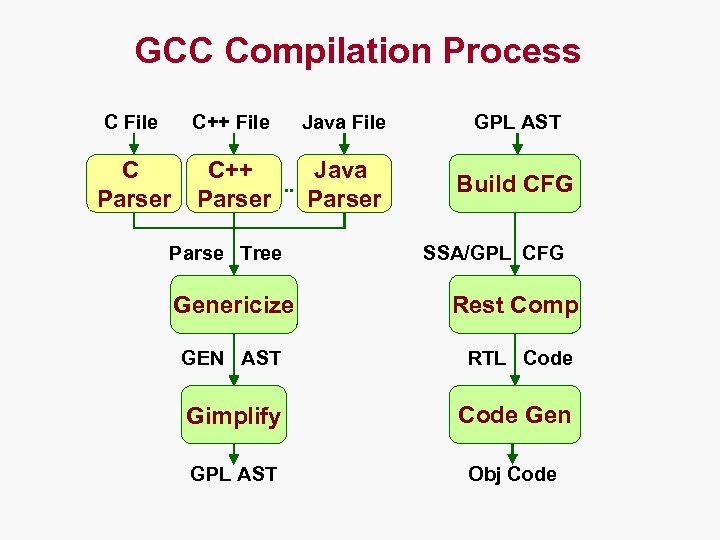GCC Compilation Process C File C++ File C Parser Java File C++ Java. . Parser Parse Tree GPL AST Build CFG SSA/GPL CFG Genericize Rest Comp GEN AST RTL Code Gimplify Code Gen GPL AST Obj Code

C Program and its GIMPLE IL int main() { int a, b, c; a = 5; b = a + 10; c = a + foo(a, b); if (a > c) c = b++/a + b*a; bar(a, b, c); } int main { int a, b, c; int T 1, T 2, T 3, T 4; a = 5; b = a + 10; T 1 = foo(a, b); T 2 = a + T 1; if (a > T 2) goto fi; T 3 = b / a; T 4 = b * a; c = T 2 + T 3; b = b + 1; fi: bar(a, b, c); }

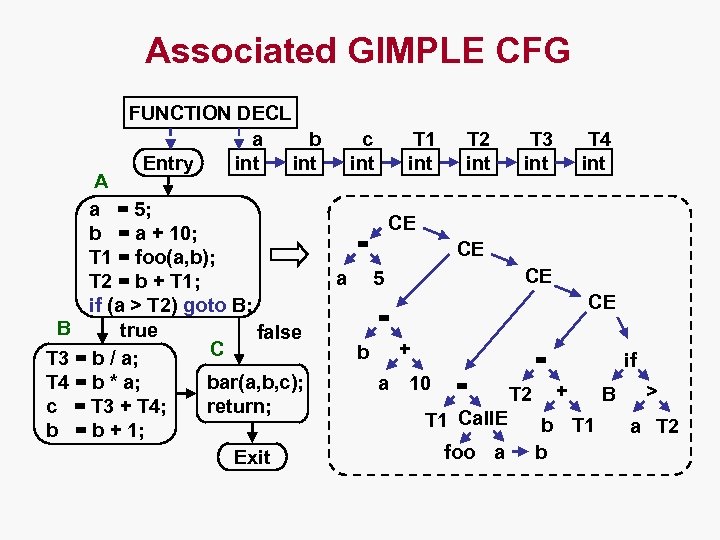Associated GIMPLE CFG FUNCTION DECL a b int Entry A a = 5; b = a + 10; T 1 = foo(a, b); T 2 = b + T 1; if (a > T 2) goto B; B true false C T 3 = b / a; bar(a, b, c); T 4 = b * a; return; c = T 3 + T 4; b = b + 1; Exit c int T 1 int T 3 int T 4 int CE = a T 2 int CE CE 5 CE = + b a = 10 = T 1 Call. E foo a T 2 if + b T 1 b B > a T 2

GCC Model Checking (GMC) • GMC: a suite of analysis and verification tools we are developing for the Tree-SSA level of GCC. Currently: – Intra-procedural slicer: in work is inter-procedural slicing. – Symbolic execution engine: for Boolean C programs. – Interpreter: traverses the CFG using Tree-SSA iterators. – Monte Carlo MC (GMC 2): OSE, randomized alg. for LTL MC. • GMC 2: a newly developed technique that uses theory of geometric random variables, statistical hypothesis testing and random sampling of lassos.

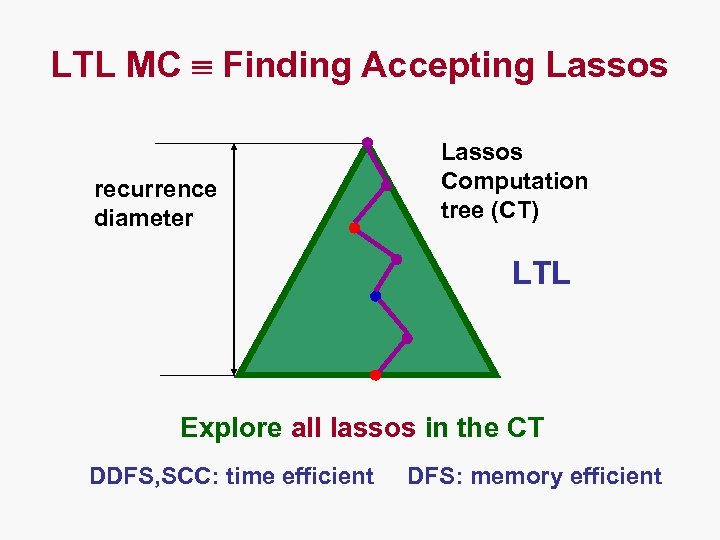LTL MC Finding Accepting Lassos recurrence diameter Lassos Computation tree (CT) LTL Explore all lassos in the CT DDFS, SCC: time efficient DFS: memory efficient

Randomized Algorithms • Takes of next step algorithm may depend on random choice (coin flip). – Benefits: simplicity, efficiency, and symmetry breaking. • Monte Carlo: may produce incorrect result but with bounded error probability. – Example: Election’s result prediction • Las Vegas: always gives correct result but running time is a random variable. – Example: Randomized Quick Sort

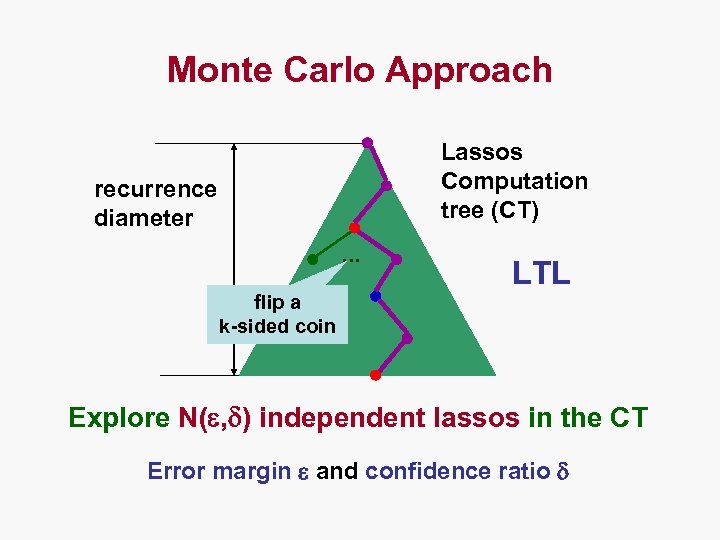Monte Carlo Approach Lassos Computation tree (CT) recurrence diameter … LTL flip a k-sided coin Explore N( , ) independent lassos in the CT Error margin and confidence ratio

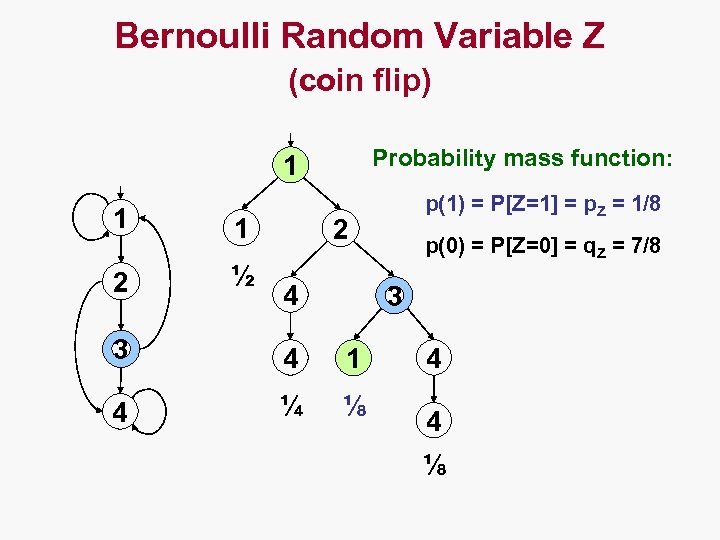Bernoulli Random Variable Z (coin flip) Probability mass function: 1 1 1 2 ½ p(1) = P[Z=1] = p. Z = 1/8 2 4 p(0) = P[Z=0] = q. Z = 7/8 3 3 4 1 4 ¼ ⅛ 4 4 ⅛

Geometric Random Variable • Value of geometric RV X with parameter pz: – No. of independent lassos until success. • Probability mass function: – p(N) = P[X = N] = qz. N-1 pz • Cumulative Distribution Function: – F(N) = P[X N] = ∑i Np(i) = 1 – qz. N = 1 – (1 - pz)N

How Many Lassos? • Requiring 1 - (1 -pz)N = 1 - δ yields: N = ln (δ) / ln (1 - pz) • Lower bound on number of trials N needed to achieve success with confidence ratio δ.

What If pz Unknown? • Requiring pz ε yields: M = ln (δ) / ln (1 - ε) N = ln (δ) / ln (1 - pz) and therefore P[X M] 1 - δ • Lower bound on number of trials M needed to achieve success with confidence ratio δ and error margin ε.

Statistical Hypothesis Testing • Null hypothesis H 0: pz ε • Alternative hypothesis H 1: pz < ε • If no success after N trials, then reject H 0 • Type I error: α = P[ X > M | H 0 ] < δ • Since: P[ X M | H 0 ] 1 - δ

Monte Carlo Model Checking (MC 2) input: B=(Σ, Q, Q 0, δ, F), ε, δ N = ln (δ) / ln (1 - ε) for (i = 1; i N; i++) if (RL(B) == 1) return (1, error-trace); return (0, “reject H 0 with α = Pr[ X>N | H 0 ] < δ”); where RL(B) performs a uniform random walk through B to obtain a random lasso.

GCC MC 2 (GMC 2) • Input: a set of CFGs. – Main function: A specifically designated CFG. • Random walks in the Büchi automaton: generated on-the-fly. – Initial state: of the main routine + bookkeeping information. – Next state: choose process + call interpreter on its CFG. – Processes: created by using the fork primitive. – Optimization: interpreter returns only upon context switch. • Lassos: detected by using a hierarchic hash table. – Local variables: removed upon return from a procedure.

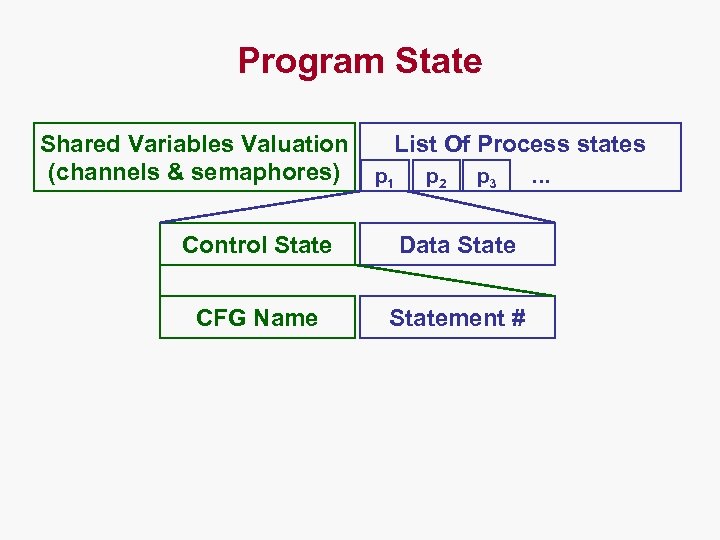Program State Shared Variables Valuation (channels & semaphores) List Of Process states p 1 p 2 p 3 Control State Data State CFG Name Statement # …

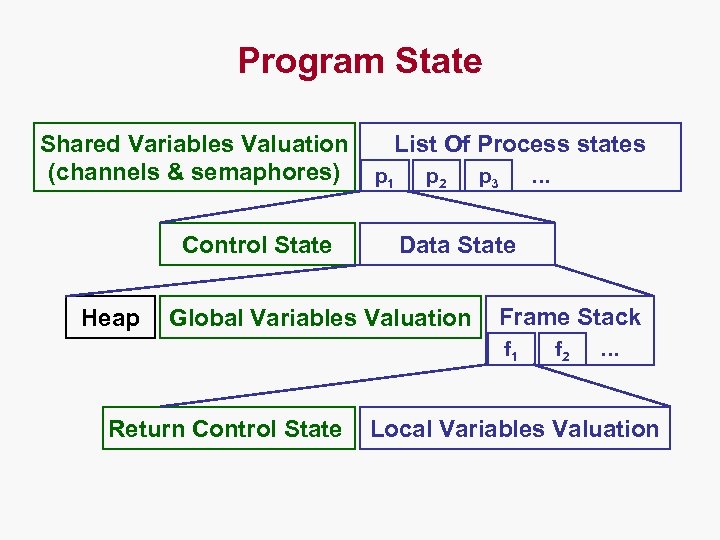Program State Shared Variables Valuation (channels & semaphores) Control State Heap List Of Process states p 1 p 2 p 3 … Data State Global Variables Valuation Frame Stack f 1 Return Control State f 2 … Local Variables Valuation

Interpreter • Interprets GIMPLE statements: according to their semantics. Interesting: – Inter-procedural: call(), return(). Manipulate the frame stack. • Catches and interprets: function calls to various modeling and concurrency primitives: – Modeling: toss(), assert(). Nondeterminism and checks. – Processes: fork(), … Manipulate the process list. – Communication: send(), recv(). Manipulate shared vars. May involve a context switch.

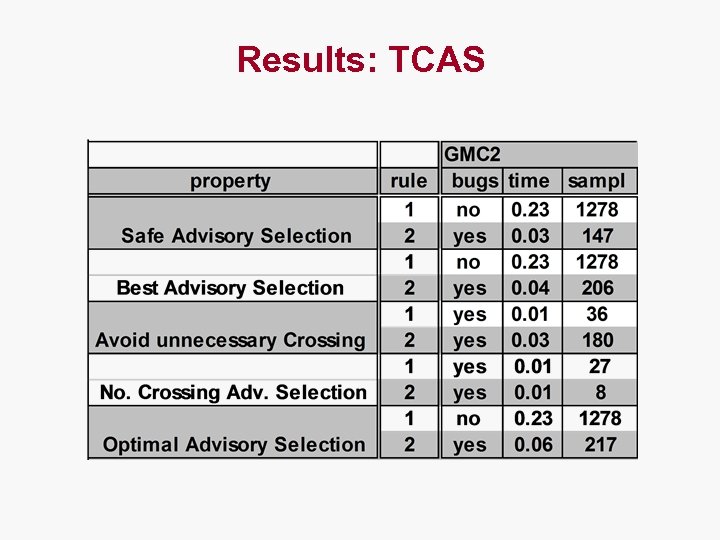Results: TCAS

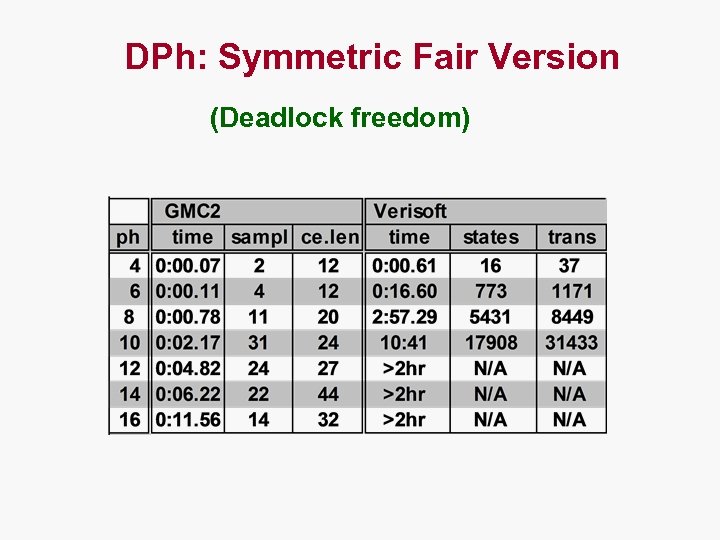DPh: Symmetric Fair Version (Deadlock freedom)

Needham-Schroeder Protocol • Quite sophisticated C implementation. • However, of a sequential nature: - Essentially executes only one round of a reactive system

Related Work • Software model checkers for concurrent C/C++: – Veri. Soft, Spin, Blast (Slam), Magic, C-Wolf. Bogor? • Cooperative Bug Isolation [Liblit, Naik & Zheng]: – Compile-time instrumentation. Distribute binaries/collect bugs. – Statistical analysis to isolate erroneous code segments. • Random interpretation [Gulvany & Necula]: – Execute random paths and merge with random linear operators. • Monte Carlo and abstract interpretation [Monniaux]: – Analyze programs with probabilistic and nondeterministic input.

Conclusions • Presented GMC 2: a software MC for GCC based on Monte Carlo MC: – At Tree-SSA level: applicable to C, C++, Ada, Java, etc. – Open source: freely available for usage/critique/extension. • Ongoing and Future Work: Create a software MC branch of GCC, which also includes: – Automated abstraction/refinement/interpolation techniques. – Currently we manually apply a form of bounded-range abstraction (e. g. in TCAS).

Talk Outline 1. Model Checking 2. Randomized Algorithms 3. LTL Model Checking 4. Probability Theory Primer 5. Monte Carlo Model Checking 6. Implementation & Results 7. Conclusions & Open Problem

Linear Temporal Logic • LTL formula: made up inductively of • atomic propositions p, boolean connectives , , • temporal modalities X (ne. Xt) and U (Until). • Safety: “nothing bad ever happens” E. g. G( (pc 1=cs pc 2=cs)) where G is a derived modality (Globally). • Liveness: “something good eventually happens” E. g. G( req F serviced ) where F is a derived modality (Finally).

Model Checking • S is a nondeterministic/concurrent system. • is a temporal logic formula. – in our case Linear Temporal Logic (LTL). • Basic idea: intelligently explore S’s state space in attempt to establish S |= .

LTL Model Checking • Every LTL formula can be translated to a Büchi automaton B such that L( ) = L(B ) • Automata-theoretic approach: S |= iff L(BS) L(B ) iff L(BS B ) = • Checking non-emptiness is equivalent to finding a reachable accepting cycle (lasso).

Emptiness Checking • Checking non-emptiness is equivalent to finding an accepting cycle reachable from initial state (lasso). • Double Depth-First Search (DDFS) algorithm can be used to search for such cycles, and this can be done on-the-fly! sn s 1 s 2 s 3 sk+2 sk-1 sk+1 sk DFS 2 DFS 1

Randomized Algorithms • Huge impact on CS: (distributed) algorithms, complexity theory, cryptography, etc. • Takes of next step algorithm may depend on random choice (coin flip). • Benefits of randomization include simplicity, efficiency, and symmetry breaking.

Lassos Probability Space • Sample Space: lassos in BS B • Bernoulli random variable Z : – Outcome = 1 if randomly chosen lasso accepting – Outcome = 0 otherwise • p. Z = ∑ p i Zi (expectation of an accepting lasso) where pi is lasso prob. (uniform random walk)

Bernoulli Random Variable (coin flip) • Value of Bernoulli RV Z: Z = 1 (success) & Z = 0 (failure) • Probability mass function: p(1) = Pr[Z=1] = pz p(0) = Pr[Z=0] = 1 - pz = qz • Expectation: E[Z] = pz

Statistical Hypothesis Testing • Example: Given a fair and a biased coin. – Null hypothesis H 0 - fair coin selected. – Alternative hypothesis H 1 - biased coin selected. • Hypothesis testing: Perform N trials. – If number of heads is LOW, reject H 0. – Else fail to reject H 0.

Statistical Hypothesis Testing H 0 is True H 0 is False reject H 0 Type I error w/prob. α Correct to reject H 0 fail to reject H 0 Correct to fail to reject H 0 Type II error w/prob. β

Random Lasso (RL) Algorithm

Correctness of MC 2 Theorem: Given a Büchi automaton B, error margin ε, and confidence ratio δ, if MC 2 rejects H 0, then its type I error has probability α = P[ X > M | H 0 ] < δ

Complexity of MC 2 Theorem: Given a Büchi automaton B having diameter D, error margin ε, and confidence ratio δ, MC 2 runs in time O(N∙D) and uses space O(D), where N = ln(δ) / ln(1 - ε) Cf. DDFS which runs in O(2|S|+|φ|) time for B = BS B .

Alternative Sampling Strategies • Multilasso sampling: ignores backedges that do not lead to an accepting lasso. 0 1 n-1 n Pr[Ln]= O(2 -n) • Probabilistic systems: there is a natural way to assign a probability to a RL. • Input partitioning: partition input into classes that trigger the same behavior (guards).