Ontologies perspectives formal languages and tools Dipartimento di

Ontologies: perspectives, formal languages and tools Dipartimento di Informatica, Sistemistica e Comunicazione Università di Milano-Bicocca bandini@disco. unimib. it tel. ale. m@disco. unimib. it matteo. palmonari@disco. unimib. it 02 6448 7835 02 6448 7879

What are Ontologies? Philosophy: • Where philosophical ontology has been concerned with the furniture and entities of reality, i. e. , with the study of “being qua being”, computer scientists have been occupied with the development of formalized, semantic, and logic-based models, which can easily be implemented in computer systems*. • ‘ontology’ may be defined as the study of being as such* *Peter Øhrstrøm, Jan Andersen, Henrik Scharfe, What Has Happened to Ontology In F. Dau, M. -L. Mugnier, G. Stumme (Eds. ): ICCS 2005, LNAI 3596, pp. 425– 438, 2005. Springer-Verlag Berlin Heidelberg 2005. Ontology, understood as a branch of metaphysics, is the science of being in general, embracing such issues as the nature of existence and the categorical structure of reality. . Different systems of ontology propose alternative categorical schemes. A categorical scheme typically exhibits a hierarchical structure, with 'being' or 'entity' as the topmost category, embracing everything that exists. Honderich, T. (Ed. ). (1995). The Oxford companion to philosophy. New York: Oxford University Press. Computer Science: An ontology is a specification of a conceptualization. T. R. Gruber. A translation approach to portable ontologies. Knowledge Acquisition, 5(2): 199 -220, 1993.

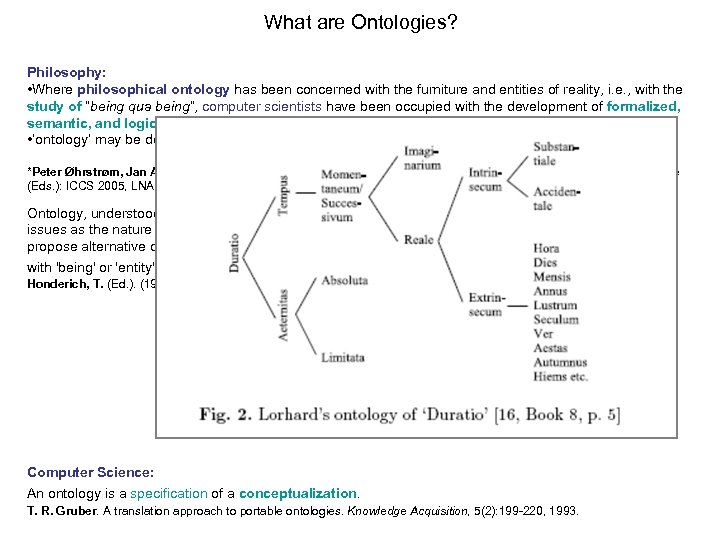What are Ontologies? Philosophy: • Where philosophical ontology has been concerned with the furniture and entities of reality, i. e. , with the study of “being qua being”, computer scientists have been occupied with the development of formalized, semantic, and logic-based models, which can easily be implemented in computer systems*. • ‘ontology’ may be defined as the study of being as such* *Peter Øhrstrøm, Jan Andersen, Henrik Scharfe, What Has Happened to Ontology In F. Dau, M. -L. Mugnier, G. Stumme (Eds. ): ICCS 2005, LNAI 3596, pp. 425– 438, 2005. Springer-Verlag Berlin Heidelberg 2005. Ontology, understood as a branch of metaphysics, is the science of being in general, embracing such The subject of ontology is the categorical structure things that Different issues as the nature of existence andstudy of the categories of of reality. . exist or systems of ontology may exist in some domain. The product of the scheme typically exhibits a propose alternative categorical schemes. A categorical study, called ”an ontology”, hierarchical structure, is a catalog of the types of things that are assumed to exist in a domain of with 'being' or 'entity' as the topmost category, embracing everything that exists. interest, D, from the perspective of a person who uses language L for the Honderich, T. (Ed. ). (1995). The Oxford companion to philosophy. New York: Oxford University Press. purpose of talking about D. Sowa, John F. : Knowledge Representation. Logical, Philosophical, and Computational Foundations, Brooks Cole Publishing Co. , Pacific Grove, CA, (2000). "[o]n the other hand, in its most prevalent use in AI, an ontology refers to an engineering artifact, constituted by a specific vocabulary used to describe a certain reality, plus a set of explicit assumptions regarding the intended meaning of the vocabulary words. " Guarino, N. : Formal Ontology in Information Systems. in: Guarino, N. (ed) Proceedings of FOIS’ 98, IOS Press, Amsterdam: Trento, Italy, pp. 3– 15, (1998). Computer Science: An ontology is a specification of a conceptualization. T. R. Gruber. A translation approach to portable ontologies. Knowledge Acquisition, 5(2): 199 -220, 1993.

Why Ontologies in CS? • Applications: – E-commerce, Ubiquitous Computing, Expert Systems, ERP, e. Government, etc • System Modeling and Design (AI and Expert Systems, Object Oriented Programming) – Which Entities need to be esplicitely represented? – Which Objects need to be represented? • Semantic Web • Integration and Interoperability • Semantic Web Services – Related to both Semantic Web and Interoperability • Information Retrieval • Natural Language Processing

Semantic Web* • • The Semantic Web aims for machine-understandable Web resources, whose information can then be shared and processed both by automated tools, such as search engines, and by human users. Sharing of information between dierent agents requires semantic mark-up, i. e. , an annotation of the Web page with information on its content that is understood by the agents searching the Web. Such an annotation will be given in some standardized, expressive language (which, e. g. , provides Boolean operators and some form of quantication) and make use of certain terms (like “Human", “Plant", etc. ). To make sure that dierent agents have a common understanding of these terms, one needs ontologies in which these terms are described, and which thus establish a joint terminology between the agents. • Basically, an ontology is a collection of denitions of concepts and the shared understanding comes from the fact that all the agents interpret the concepts w. r. t. the same ontology. • Reasoning is important to ensure the quality of an ontology ! *Franz Baader, Ian Horrocks, and Ulrike Sattler. Description logics as ontology languages for the semantic web. In Lecture Notes in Artificial Intelligence 2605, pages 228 -248. Springer, 2005.

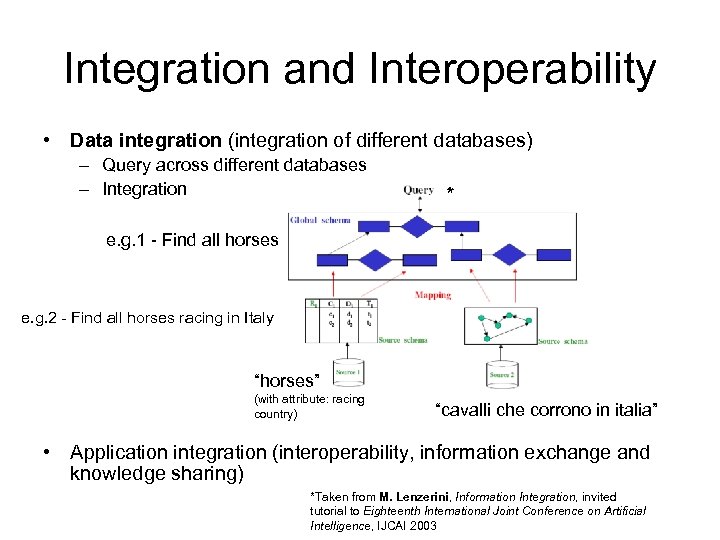Integration and Interoperability • Data integration (integration of different databases) – Query across different databases – Integration * e. g. 1 - Find all horses e. g. 2 - Find all horses racing in Italy “horses” (with attribute: racing country) “cavalli che corrono in italia” • Application integration (interoperability, information exchange and knowledge sharing) *Taken from M. Lenzerini, Information Integration, invited tutorial to Eighteenth International Joint Conference on Artificial Intelligence, IJCAI 2003

Service Oriented Computing with Semantic Web Services • Interoperability through Service Oriented Application: – WS publishing, discovery, selection, composition, execution • Annotation of resources (services): – – Semantic descriptions of the offered services Semantic specification of user’s goal Discovery of w-services basd on semantic matching Semantic based mediations • e. g. when Looking for a WS selling a trip to france. . . . pick up a service offering a trip to Paris, Lyon, Nice. . Not pick up a service offering a trip from Paris to Bruxels • Require the specification of – what is a trip; where is Paris, Lyon, Nice, Bruxels (relationship between “France” and cities within France)

E. G: Virtual Travel Agency Service Description* • book tickets, hotels, amenities, etc. • capability description (pre-state) capability VTAcapability shared. Variables {? credit. Card, ? initial. Balance, ? item, ? passenger} precondition defined. By ? reservation. Request[ reservation. Item has. Value ? item, passenger has. Value ? passenger, payment has. Value ? creditcard, ] member. Of tr#reservation. Request and ((? item member. Of tr#trip) or (? item member. Of tr#ticket)) and ? credit. Card[balance has. Value ? initial. Balance] member. Of po#credit. Card. assumption defined. By po#valid. Credit. Card(? credit. Card) and (? credit. Card[type has. Value po#visa] or ? credit. Card[type has. Value po#mastercard]). *Taken from DERI-WSMO: Web Service Tutorial at ISWC 05

How to represent Ontologies? • Need for languages. . . formal, machine readable, (standardized? ) for the ontological representations: – – Concepts. . . Conceptual entities of a domain (e. g. Horse) Properties. . . Attributes describing concepts (e. g. has. Color) Relations. . . Relations among concepts (e. g. Is-A [Animal]) Axioms. . . Constraints and committments on the ontological representation (e. g. No horse is a human) – Individuals and memberships (e. g. Furia is a Horse) • Reasoning is important to • Ensure the quality of an ontology during ontology design – it can be used to test whether concepts are non-contradictory and to derive implied relations. – test whether the concept denitions in the ontology have the intended consequences or not. • When searching Web pages, data and documents annotated with such concepts. – E. g. Want to find all resources about Funky Music • • Pick up also those about Deep Funk, Afro-Soul (i. e. subconcept) Pick up also those about Soul Music (i. e. similar concept) Artificial Intelligence and KR has a long tradition!

FOL ! Termini Formule Atomiche Formule ben formate GREAT EXPRESSIVITY, BUT WHAT ABOUT REASONING? Many Calculi, but computability problems! FOL is undecidable!

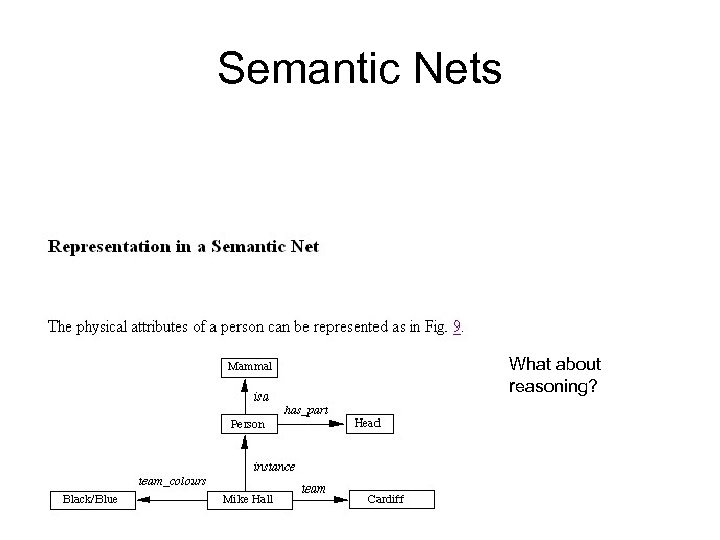Semantic Nets What about reasoning?

E. g. Frame What about reasoning?

E. g. Logic Programming What about reasoning? % Sfumatura di località con relazione di contiguità (simmetrica, riflessiva). La vicinanza non è transitiva. vicino(LUOGO, LUOGO) : - luogo(LUOGO). vicino(LUOGO_2, LUOGO_1) : - vicino(LUOGO_1, LUOGO_2), luogo(LUOGO_1), luogo(LUOGO_2). -vicino(L 1, L 2) : - not vicino(L 1, L 2), luogo(L 1), luogo(L 2). % La coincidenza spaziale è una relazione di equivalenza tra luoghi. coincide(L, L) : - luogo(L). coincide(L 1, L 2) : - luogo(L 1), luogo(L 2), coincide(L 2, L 1). coincide(L 1, L 3) : - coincide(L 1, L 2), coincide(L 2, L 3), luogo(L 1), luogo(L 2), luogo(L 3). -coincide(L 1, L 2) : - not coincide(L 1, L 2), luogo(L 1), luogo(L 2).

Ontologies • Conceptual Modeling • Representation + Reasoning – Not FOL: BALANCE between Expressiveness and Computational Acceptable Behavior • Semantic, machine-readable annotation of data, documents, resources (Semantic Web, SOC, Information retrieval, Ubiquitous Computing, . . . )

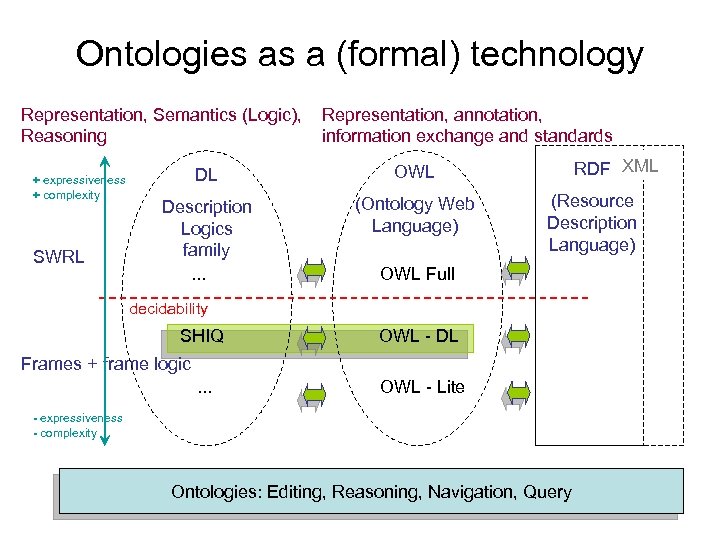Ontologies as a (formal) technology Representation, Semantics (Logic), Reasoning + expressiveness + complexity SWRL Representation, annotation, information exchange and standards DL Description Logics family. . . (Ontology Web Language) RDF XML OWL (Resource Description Language) OWL Full decidability SHIQ OWL - DL Frames + frame logic. . . OWL - Lite - expressiveness - complexity Ontologies: Editing, Reasoning, Navigation, Query

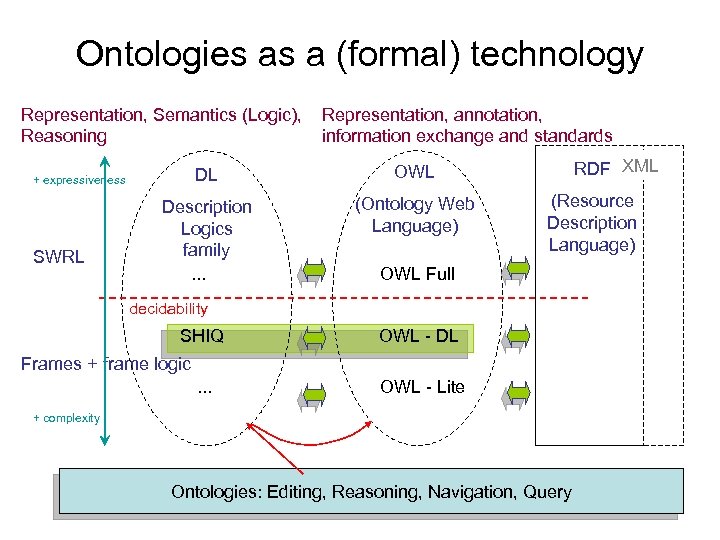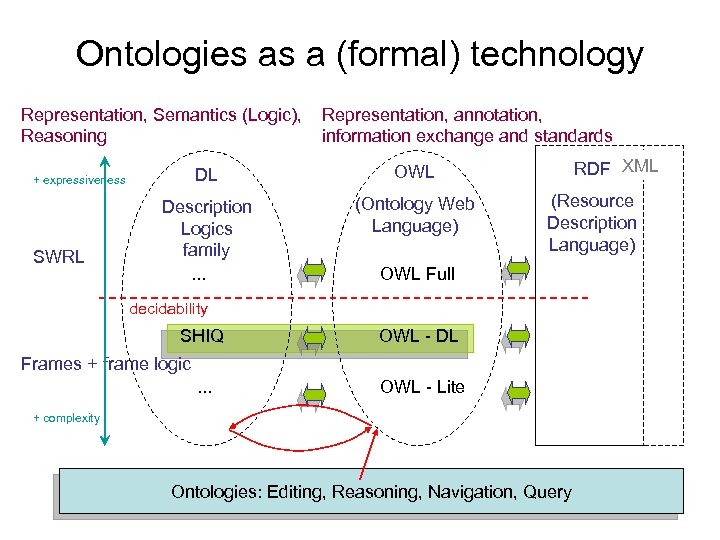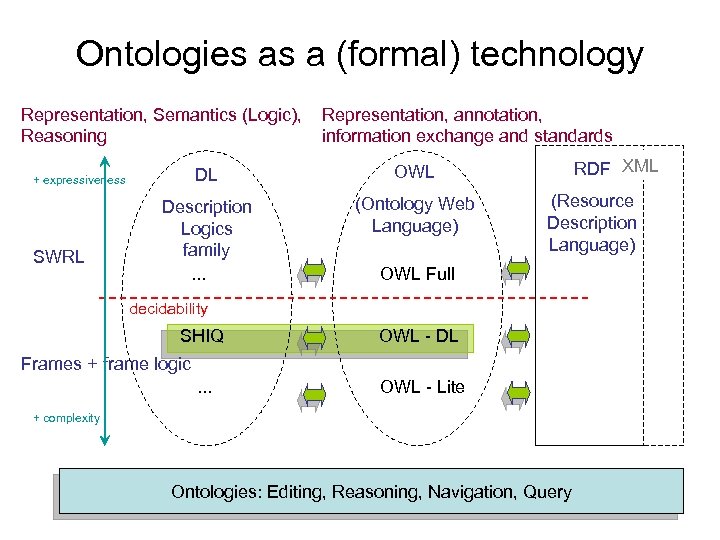Ontologies as a (formal) technology Representation, Semantics (Logic), Reasoning DL Description Logics family. . . (Ontology Web Language) RDF XML OWL + expressiveness SWRL Representation, annotation, information exchange and standards (Resource Description Language) OWL Full decidability SHIQ OWL - DL Frames + frame logic. . . OWL - Lite + complexity Ontologies: Editing, Reasoning, Navigation, Query

Logic Frames Semantic Nets Modeling: major representational focus. . . – Concepts. . . Conceptual entities of a domain (e. g. Horse) – Properties. . . Attributes describing concepts (e. g. has. Color) – Relations. . . Relations among concepts (e. g. Is-A [Animal]) – Axioms. . . Constraints and committments on the ontological representation (e. g. No horse is a human) – Individuals and memberships (e. g. Furia is a Horse)

RDF • Resource Description Language: to associate metadata to resources available on the web – XML sysntax (restrictions from a specific DTD) – Statements: subject – predicate – object • E. g. Document 1 is-about Horses – Uniform Resource Identifier (URI) to identify everything we want to talk URI about (resources) – Everything can be a resource: • • A piece of information A document A concept of a paticular ontology. . . – Subject / predicate / object are all resources. • E. g. http: //www. aaaa. it/document 1. html rdf: is. About http: //www. bbbb. it/Ontology/Horse • Still no reasoning! What is the difference between rdf: type / rdf: creator / rdf: is. About For the full RDF syntax see RDF/XML Syntax Specification [http: //www. w 3. org/TR/rdf-syntax-grammar/]

OWL Web Ontology Language Guide W 3 C Recommendation 10 February 2004 Obiettivi 1. 2. 3. Formalize a domain by defining classes and properties of those classes, define individuals and assert properties about them, and reason about these classes and individuals to the degree permitted by the formal semantics of the OWL language. "Tell me what wines I should buy to serve with each course of the following menu. And, by the way, I don't like Sauternes. “ To support this sort of computation, it is necessary to go beyond keywords and specify the meaning of the resources described on the Web. This additional layer of interpretation captures the semantics of the data. An OWL ontology may include descriptions of classes, properties and their instances. Given such an ontology, the OWL formal semantics specifies how to derive its logical consequences, i. e. facts not literally present in the ontology, but entailed by the semantics.

The Species of OWL Three increasingly expressive sublanguages OWL Lite supports those users primarily needing a classification hierarchy and simple constraint features. For example, while OWL Lite supports cardinality constraints, it only permits cardinality values of 0 or 1. It should be simpler to provide tool support for OWL Lite than its more expressive relatives, and provide a quick migration path for thesauri and other taxonomies. OWL DL supports those users who want the maximum expressiveness without losing computational completeness (all entailments are guaranteed to be computed) and decidability (all computations will finish in finite time) of reasoning systems. OWL DL includes all OWL language constructs with restrictions such as type separation (a class can not also be an individual or property, a property can not also be an individual or class). OWL DL is so named due to its correspondence with description logics [Description Logics], a field of research that has studied a particular decidable fragment of first order logic. OWL DL was designed to support the existing Description Logic business segment and has desirable computational properties for reasoning systems. OWL Full is meant for users who want maximum expressiveness and the syntactic freedom of RDF with no computational guarantees. For example, in OWL Full a class can be treated simultaneously as a collection of individuals and as an individual in its own right. Another significant difference from OWL DL is that a owl: Datatype. Property can be marked as an owl: Inverse. Functional. Property. OWL Full allows an ontology to augment the meaning of the pre-defined (RDF or OWL) vocabulary. It is unlikely that any reasoning software will be able to support every feature of OWL Full. The choice between OWL Lite and OWL DL depends on the extent to which users require the more expressive restriction constructs provided by OWL DL. Reasoners for OWL Lite will have desirable computational properties. Reasoners for OWL DL, while dealing with a decidable sublanguage, will be subject to higher worst-case complexity. The choice between OWL DL and OWL Full mainly depends on the extent to which users require the meta-modelling facilities of RDF Schema (i. e. defining classes of classes). When using OWL Full as compared to OWL DL, reasoning support is less predictable.

Simple Named Classes The most basic concepts in a domain should correspond to classes that are the roots of various taxonomic trees. Every individual in the OWL world is a member of the class owl: Thing. Thus each user-defined class is implicitly a subclass of owl: Thing. Domain specific root classes are defined by simply declaring a named class. OWL also defines the empty class, owl: Nothing. owl: Thing Name Specification owl: Nothing And while the classes exist, they may have no members. For all we know at the moment, these classes might as well have been called Thing 1, Thing 2, and Thing 3

Taxonomic Constructor for Classes rdfs: sub. Class. Of The fundamental taxonomic constructor for classes is rdfs: sub. Class. Of. It relates a more specific class to a more general class. If X is a subclass of Y, then every instance of X is also an instance of Y. The rdfs: sub. Class. Of relation is transitive (if X is a subclass of Y and Y a subclass of Z then X is a subclass of Z . . . We define Potable. Liquid (liquids suitable for drinking) to be a subclass of Consumable. Thing Potable. Liquid A class definition has two parts: a name introduction or reference and a list of restrictions. Each of the immediate contained expressions in the class definition further restricts the instances of the defined class. Instances of the class belong to the intersection of the restrictions.

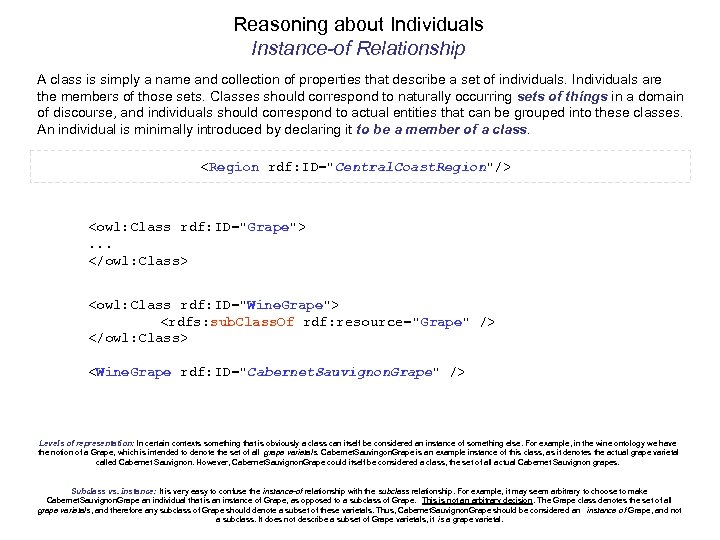Reasoning about Individuals Instance-of Relationship A class is simply a name and collection of properties that describe a set of individuals. Individuals are the members of those sets. Classes should correspond to naturally occurring sets of things in a domain of discourse, and individuals should correspond to actual entities that can be grouped into these classes. An individual is minimally introduced by declaring it to be a member of a class. . . . Levels of representation: In certain contexts something that is obviously a class can itself be considered an instance of something else. For example, in the wine ontology we have the notion of a Grape, which is intended to denote the set of all grape varietals. Cabernet. Sauvingon. Grape is an example instance of this class, as it denotes the actual grape varietal called Cabernet Sauvignon. However, Cabernet. Sauvignon. Grape could itself be considered a class, the set of all actual Cabernet Sauvignon grapes. Subclass vs. instance: It is very easy to confuse the instance-of relationship with the subclass relationship. For example, it may seem arbitrary to choose to make Cabernet. Sauvignon. Grape an individual that is an instance of Grape, as opposed to a subclass of Grape. This is not an arbitrary decision. The Grape class denotes the set of all grape varietals, and therefore any subclass of Grape should denote a subset of these varietals. Thus, Cabernet. Sauvignon. Grape should be considered an instance of Grape, and not a subclass. It does not describe a subset of Grape varietals, it is a grape varietal.

Object Properties let us assert general facts about the members of classes and specific facts about individuals. A property is a binary relation. [1] [2] object properties, relations between instances of two classes (individuals to individuals) datatype properties, relations between instances of classes (individuals to datatypes) Thing made. From. Grape Wine. Grape Thing

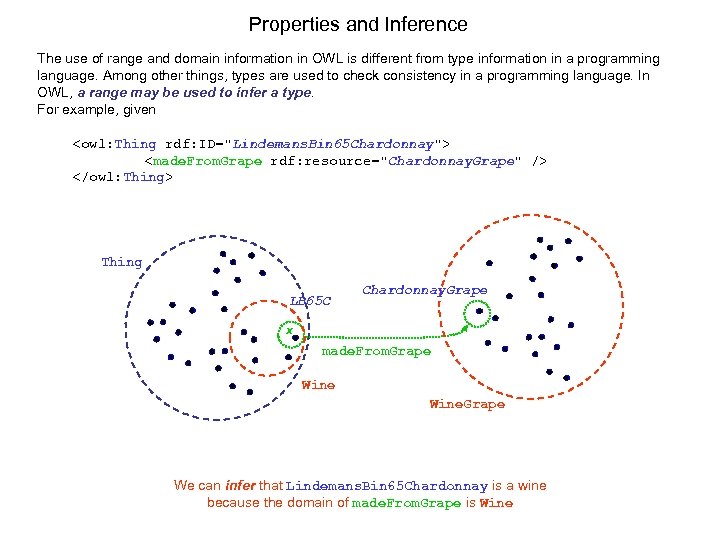Properties and Inference The use of range and domain information in OWL is different from type information in a programming language. Among other things, types are used to check consistency in a programming language. In OWL, a range may be used to infer a type. For example, given Thing LB 65 C Chardonnay. Grape x made. From. Grape Wine. Grape We can infer that Lindemans. Bin 65 Chardonnay is a wine because the domain of made. From. Grape is Wine

Taxonomy of Properties Property hierarchies may be created by making one or more statements that a property is a subproperty of one or more other properties . . . Wine. Descriptor properties relate wines to their color and components of their taste, including sweetness, body, and flavor. . . . has. Color is a subproperty of the has. Wine. Descriptor property, with its range further restricted to Wine. Color

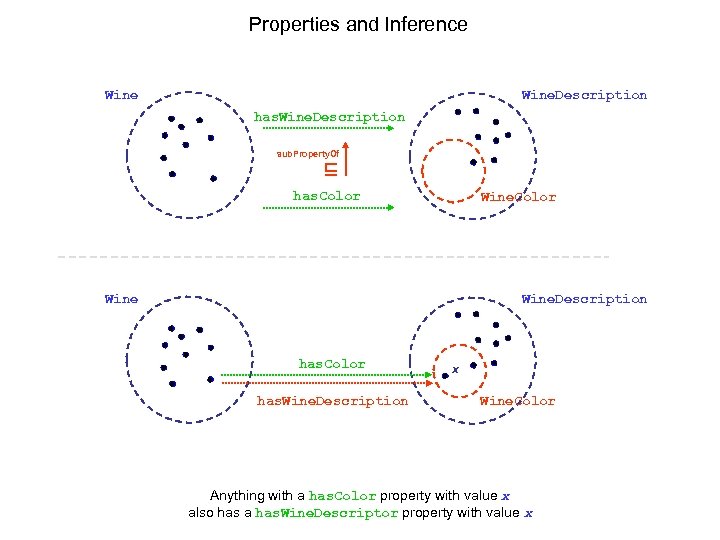Properties and Inference Wine. Description Wine has. Wine. Description sub. Property. Of ⊑ has. Color Wine. Description Wine has. Color has. Wine. Description x Wine. Color Anything with a has. Color property with value x also has a has. Wine. Descriptor property with value x

At least, At most Restrictions [OWL Lite] Cardinality is useful to state that a property on a class has both min. Cardinality 0 and max. Cardinality 0 or both min. Cardinality 1 and max. Cardinality 1 1 A wine is made from at least one Wine. Grape . . . Anonymous. Class Wine made. From. Grape ≥ 1 Potable. Liquid Wine. Grape

Properties of Individuals <Region rdf: ID= Properties of Individuals located. In Santa. Cruz. Mountains. Region Santa. Cruz. Mountain. Vineyard Cabernet. Sauvignon has. Maker Santa. Cruz. Mountain. Vineyard

Properties Characteristics inverse. Of One property may be stated to be the inverse of another property. If the property P 1 is stated to be the inverse of the property P 2, then if X is related to Y by the P 2 property, then Y is related to X by the P 1 property Transitive. Property Properties may be stated to be transitive. If a property is transitive, then if the pair (x, y) is an instance of the transitive property P, and the pair (y, z) is an instance of P, then the pair (x, z) is also an instance of P OWL Lite (and OWL DL) impose the side condition that transitive properties (and their superproperties) cannot have a max. Cardinality 1 restriction. Without this side-condition, OWL Lite and OWL DL would become undecidable languages. Symmetric. Property Properties may be stated to be symmetric. If a property is symmetric, then if the pair (x, y) is an instance of the symmetric property P, then the pair (y, x) is also an instance of P Functional. Property P(x, y) and P(x, z) implies y = z Properties may be stated to have a unique value. If a property is a Functional. Property, then it has no more than one value for each individual (it may have no values for an individual). This characteristic has been referred to as having a unique property. Functional. Property is shorthand for stating that the property's minimum cardinality is zero and its maximum cardinality is 1. Inverse. Functional. Property P(y, x) and P(z, x) implies y = z Properties may be stated to be inverse functional. If a property is inverse functional then the inverse of the property is functional. Thus the inverse of the property has at most one value for each individual. This characteristic has also been referred to as an unambiguous property

Symmetric. Property <owl: Object. Property rdf: ID= " src="https://present5.com/presentation/350120e28b4c5dca2eb8414c4aa6359a/image-35.jpg" alt="Symmetric. Property " /> Symmetric. Property The Mendocino. Region is adjacent to the Sonoma. Region and vice-versa. The Mendocino. Region is located in the California. Region but not vice versa. Transitive. Property Because the Santa. Cruz. Mountains. Region is located. In the California. Region, then it must also be located. In the USRegion, since located. In is transitive

Property Restrictions all. Values. From The restriction all. Values. From is stated on a property with respect to a class. It means that this property on this particular class has a local range restriction associated with it. Thus if an instance of the class is related by the property to a second individual, then the second individual can be inferred to be an instance of the local range restriction class . . . . . . For all wines, if they have makers, all the makers are wineries some. Values. From The restriction some. Values. From is stated on a property with respect to a class. A particular class may have a restriction on a property that at least one value for that property is of a certain type . . . For all wines, they have at least one maker that is a winery

Equality and Inequality equivalent. Class Two classes may be stated to be equivalent. Equivalent classes have the same instances. Equality can be used to create synonymous classes. For example, Car can be stated to be equivalent. Class to Automobile. From this a reasoner can deduce that any individual that is an instance of Car is also an instance of Automobile and vice versa. equivalent. Property Two properties may be stated to be equivalent. Equivalent properties relate one individual to the same set of other individuals. Equality may be used to create synonymous properties. For example, has. Leader may be stated to be the equivalent. Property to has. Head. From this a reasoner can deduce that if X is related to Y by the property has. Leader, X is also related to Y by the property has. Head and vice versa. A reasoner can also deduce that has. Leader is a subproperty of has. Head and has. Head is a sub. Property of has. Leader. same. As Two individuals may be stated to be the same. These constructs may be used to create a number of different names that refer to the same individual. For example, the individual Deborah may be stated to be the same individual as Deborah. Mc. Guinness. different. From An individual may be stated to be different from other individuals. For example, the individual Frank may be stated to be different from the individuals Deborah and Jim. Thus, if the individuals Frank and Deborah are both values for a property that is stated to be functional (thus the property has at most one value), then there is a contradiction. Explicitly stating that individuals are different can be important in when using languages such as OWL (and RDF) that do not assume that individuals have one and only one name. For example, with no additional information, a reasoner will not deduce that Frank and Deborah refer to distinct individuals. All. Different A number of individuals may be stated to be mutually distinct in one All. Different statement. For example, Frank, Deborah, and Jim could be stated to be mutually distinct using the All. Different construct. Unlike the different. From statement above, this would also enforce that Jim and Deborah are distinct (not just that Frank is distinct from Deborah and Frank is distinct from Jim). The All. Different construct is particularly useful when there are sets of distinct objects and when modelers are interested in enforcing the unique names assumption within those sets of objects. It is used in conjunction with distinct. Members to state that all members of a list are distinct and pairwise disjoint.

Beyond OWL Lite OWL DL & OWL Full one. Of (enumerated classes) Classes can be described by enumeration of the individuals that make up the class. The members of the class are exactly the set of enumerated individuals; no more, no less. For example, the class of days. Of. The. Week can be described by simply enumerating the individuals Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday. From this a reasoner can deduce the maximum cardinality (7) of any property that has days. Of. The. Week as its all. Values. From restriction. has. Value (property values) A property can be required to have a certain individual as a value (also sometimes referred to as property values). For example, instances of the class of dutch. Citizens can be characterized as those people that have the. Netherlands as a value of their nationality. (The nationality value, the. Netherlands, is an instance of the class of Nationalities). disjoint. With Classes may be stated to be disjoint from each other. For example, Man and Woman can be stated to be disjoint classes. From this disjoint. With statement, a reasoner can deduce an inconsistency when an individual is stated to be an instance of both and similarly a reasoner can deduce that if A is an instance of Man, then A is not an instance of Woman. union. Of, complement. Of, intersection. Of (Boolean combinations) OWL DL and OWL Full allow arbitrary Boolean combinations of classes and restrictions: union. Of, complement. Of, and intersection. Of. For example, using union. Of, we can state that a class contains things that are either USCitizens or Dutch. Citizens. Using complement. Of, we could state that children are not Senior. Citizens. (i. e. the class Children is a subclass of the complement of Senior. Citizens). Citizenship of the European Union could be described as the union of the citizenship of all member states. min. Cardinality, max. Cardinality, cardinality (full cardinality) While in OWL Lite, cardinalities are restricted to at least, at most or exactly 1 or 0, full OWL allows cardinality statements for arbitrary non-negative integers. complex classes In many constructs, OWL Lite restricts the syntax to single class names (e. g. in sub. Class. Of or equivalent. Class statements). OWL Full extends this restriction to allow arbitrarily complex class descriptions, consisting of enumerated classes, property restrictions, and Boolean combinations. Also, OWL Full allows classes to be used as instances (and OWL DL and OWL Lite do not). For more on this topic, see the "Design for Use" section of the Guide document.

Representation, Semantics, Reasoning: Description Logics

Representation, Semantics, Reasoning: Description Logics • DL: a family of logics. • Basically: – Concepts + Relations – Axioms: about relations among concepts • Definitions, Subclasses, Constraints – Set theory perspective • Different DLs with different Expressiveness/Complexity trade offs – Expressivity: fragments of FOL – Reasoning: Well known complexity analysis results; some DLs provide a good balance between Exp/Comp

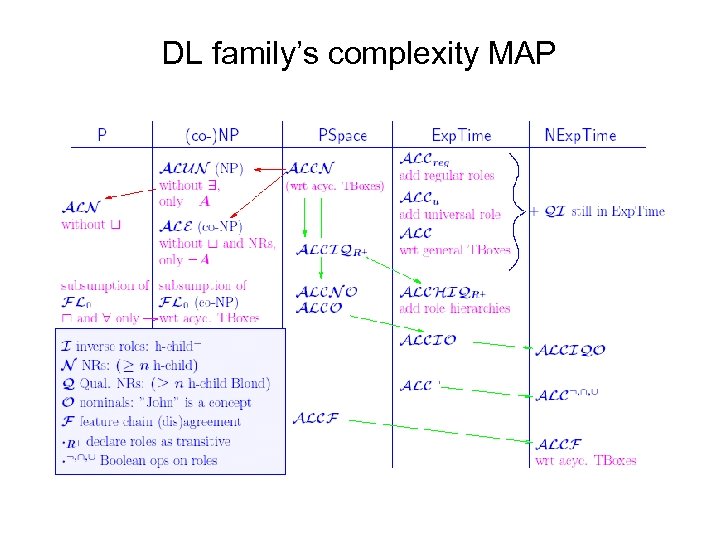DL family’s complexity MAP

Use a (Description) Logic • OWL DL based on – In fact it is equivalent to Description Logic DL • OWL DL Benefits from many years of DL research – – Well defined semantics Formal properties well understood (complexity, decidability) Known reasoning algorithms Implemented systems (highly optimised) • In fact there are three “species” of OWL (!) – OWL FULL is union of OWL syntax and RDF – OWL DL restricted OWL full to First Order fragment (≈ DAML+OIL) – OWL Lite is “simpler” subset of OWL DL (equiv to )

Class/Concept Constructors • • C is a concept (class); P is a role (property); x is an individual name XMLS datatypes as well as classes in 8 P. C and 9 P. C – Restricted form of DL concrete domains

Semantics (cont. ) • Interpretation function extends to concept (and role) expressions in the obvious way, i. e. :

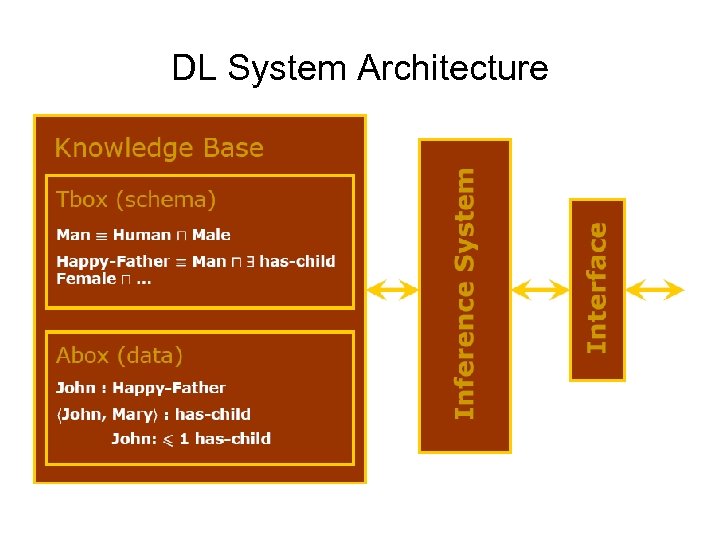DL System Architecture

Ontology/Tbox Axioms • Obvious FO/Modal Logic equivalences – E. g. , DL: C v D FOL: x. C(x) !D(x) ML: C!D • Often distinguish two kinds of Tbox axioms – “Definitions” C v D or C ´ D where C is a concept name – General Concept Inclusion axioms (GCIs) where C may be complex

Ontology Facts / Abox Axioms • Note: using nominals (e. g. , in SHOIN), can reduce Abox axioms to concept inclusion axioms equivalent to

RDFS Syntax <owl: Class> <owl: intersection. Of rdf: parse. Type= RDFS Syntax

Ontology Editing • With state of the art editors (e. g. Protegè): – Graphical support for design and editing (for TBox and ABox) • Editing and representation with Description Logic syntax and automatic generation of OWL and RDF code • Basic checks (e. g. OWL dialect) • Visualization Tools – Integration with state of the art reasoners, rule based systems and query systems

Basic Inference Tasks: pragmatically. . • Consistency checks (TBox/ABox) • Infer new relations (e. g. from transitive, symmetric or inverse properties) • Infer Hierarchies (via subsumption) • Infer type of individuals (based on axioms)

Resources • Slides from this talk – http: //www. cs. man. ac. uk/~horrocks/Slides/lpar 04. ppt • Fa. CT system (open source) – http: //www. cs. man. ac. uk/Fa. CT/ • Oil. Ed (open source) – http: //oiled. man. ac. uk/ • Protégé – http: //protege. stanford. edu/plugins/owl/ • W 3 C Web-Ontology (Web. Ont) working group (OWL) – http: //www. w 3. org/2001/sw/Web. Ont/ • The DL Handbook, Cambridge University Press – http: //books. cambridge. org/0521781760. htm

Example Ontology (Protégé)

Example Ontology (Oil. Ed)