f33c39e37fa956517d96906e530573fc.ppt
- Количество слайдов: 183

Online Learning for Real-World Problems Koby Crammer University of Pennsylvania 1

Thanks • • 2 Ofer Dekel Josheph Keshet Shai Shalev-Schwatz Yoram Singer • • • Axel Bernal Steve Caroll Mark Dredze Kuzman Ganchev Ryan Mc. Donald Artemis Hatzigeorgiu Fernando Pereira Fei Sha Partha Pratim Talukdar
Tutorial Context SVMs Real-World Data Online Learning Tutorial Optimization Theory 3 Multicass, Structured

Online Learning Tyrannosaurus rex 4

Online Learning Triceratops 5

Online Learning Velocireptor Tyrannosaurus rex 6

Formal Setting – Binary Classification • Instances – Images, Sentences • Labels – Parse tree, Names • Prediction rule – Linear predictions rules • Loss – No. of mistakes 7

Predictions • Discrete Predictions: – Hard to optimize • Continuous predictions : – Label – Confidence 8

Loss Functions • Natural Loss: – Zero-One loss: • Real-valued-predictions loss: – Hinge loss: – Exponential loss (Boosting) – Log loss (Max Entropy, Boosting) 9

Loss Functions Hinge Loss Zero-One Loss 1 1 10

Online Framework • Initialize Classifier • Algorithm works in rounds • On round the online algorithm : – – – Receives an input instance Outputs a prediction Receives a feedback label Computes loss Updates the prediction rule • Goal : 11 – Suffer small cumulative loss

Linear Classifiers • Any Features • W. l. o. g. • Binary Classifiers of the form Notation 12 Abuse

Linear Classifiers (cntd(. • Prediction: • Confidence in prediction: 13

Margin • Margin of an example classifier : with respect to the • Note : • The set there exists such that 14 is separable iff

Geometrical Interpretation 15
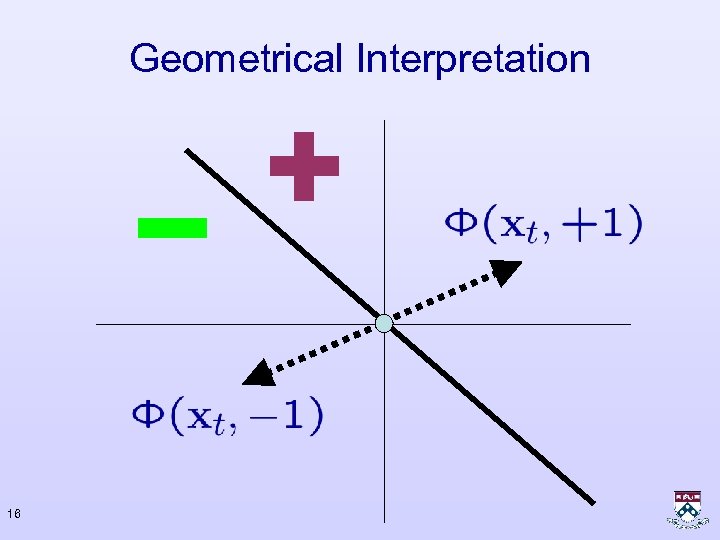
Geometrical Interpretation 16
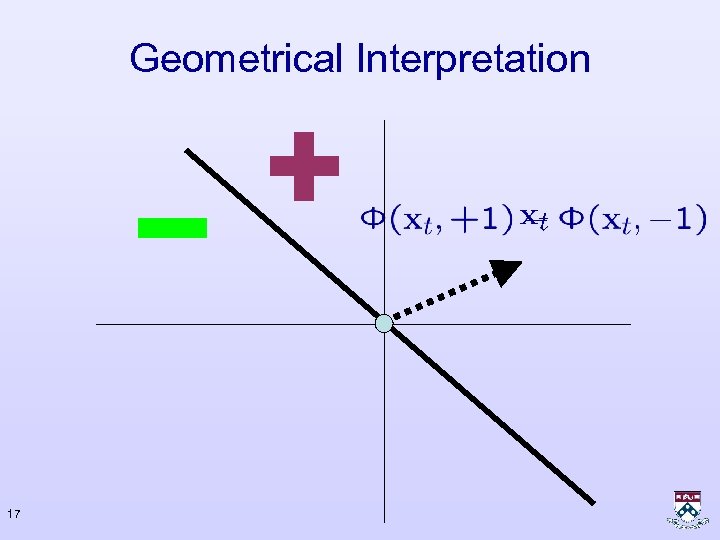
Geometrical Interpretation 17
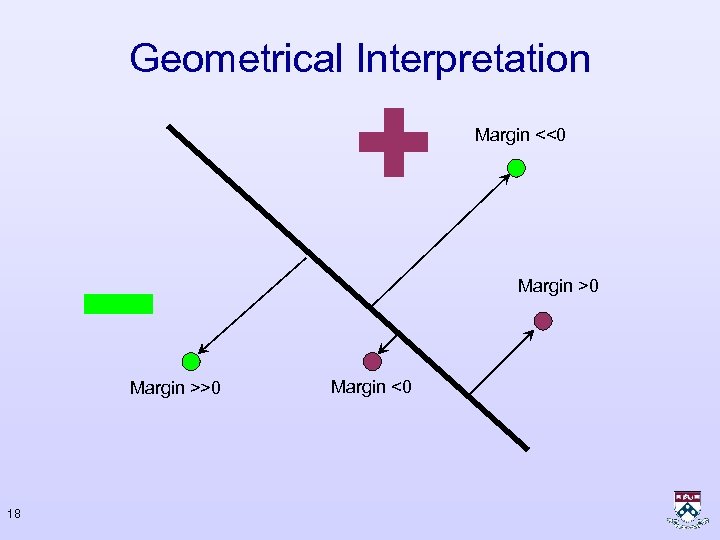
Geometrical Interpretation Margin <<0 Margin >>0 18 Margin <0

Hinge Loss 19

Separable Set 20
Inseparable Sets 21

Degree of Freedom - I The same geometrical hyperplane can be represented by many parameter vectors 22
Degree of Freedom - II Problem difficulty does not change if we shrink or expand the input 23 space

Why Online Learning? • Fast • Memory efficient - process one example at a time • Simple to implement • Formal guarantees – Mistake bounds • Online to Batch conversions • No statistical assumptions • Adaptive • Not as good as a well designed batch algorithms 24

Update Rules • Online algorithms are based on an update rule which defines from (and possibly other information) • Linear Classifiers : find from based on the input • Some Update Rules : – – 25 Perceptron (Rosenblat) ALMA (Gentile) ROMMA (Li & Long) NORMA (Kivinen et. al) – MIRA (Crammer & Singer) – EG (Littlestown and Warmuth) – Bregman Based (Warmuth)

Three Update Rules • The Perceptron Algorithm : – Agmon 1954; Rosenblatt 1952 -1962, Block 1962, Novikoff 1962, Minsky & Papert 1969, Freund & Schapire 1999, Blum & Dunagan 2002 • Hildreth’s Algorithm : – Hildreth 1957 – Censor & Zenios 1997 – Herbster 2002 • Loss Scaled : – Crammer & Singer 2001, – Crammer & Singer 2002 26

The Perceptron Algorithm • If No-Mistake – Do nothing • If Mistake – Update • Margin after update : 27
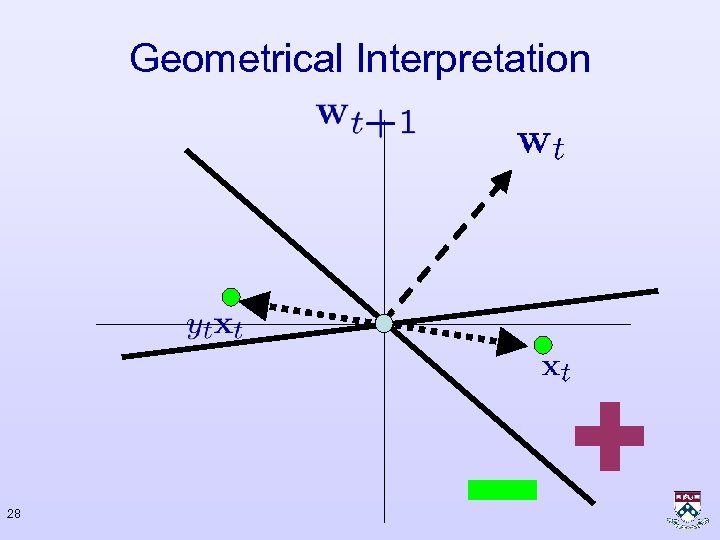
Geometrical Interpretation 28

Relative Loss Bound • For any competitor prediction function • We bound the loss suffered by the algorithm with the loss suffered by Cumulative Loss Suffered by the Algorithm 29 Sequence of Prediction Functions Cumulative Loss of Competitor

Relative Loss Bound • For any competitor prediction function • We bound the loss suffered by the algorithm with the loss suffered by Inequality Possibly Large Gap 30 Regret Extra Loss Competitiveness Ratio

Relative Loss Bound • For any competitor prediction function • We bound the loss suffered by the algorithm with the loss suffered by Grows With T 31 Constant

Relative Loss Bound • For any competitor prediction function • We bound the loss suffered by the algorithm with the loss suffered by Best Prediction Function in hindsight for the data sequence 32

Remarks • If the input is inseparable, then the problem of finding a separating hyperplane which attains less then M errors is NP-hard (Open hemisphere) • Obtaining a zero-one loss bound with a unit competitiveness ratio is as hard as finding a constant approximating error for the Open Hemisphere problem. • Bound of the number of mistakes the perceptron makes with the hinge loss of any competitor 33

Definitions • Any Competitor • The parameters vector the input data can be chosen using • The parameterized hinge loss of • True hinge loss • 1 -norm and 2 -norm of hinge loss 34 on

Geometrical Assumption • All examples are bounded in a ball of radius R 35

Perceptron’s Mistake Bound • Bounds: • If the sample is separable then 36
![[FS 99, SS 05] Proof - Intuition • Two views : – The angle [FS 99, SS 05] Proof - Intuition • Two views : – The angle](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-37.jpg)
[FS 99, SS 05] Proof - Intuition • Two views : – The angle between and decreases with – The following sum is fixed as we make more mistakes, our solution is better 37
![[C 04] Proof • Define the potential : • Bound it’s cumulative sum and [C 04] Proof • Define the potential : • Bound it’s cumulative sum and](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-38.jpg)
[C 04] Proof • Define the potential : • Bound it’s cumulative sum and below 38 from above

Proof • Bound from above: Telescopic Sum 39 Zero Vector Non-Negative

Proof • Bound From Below : – No error on tth round – Error on tth round 40

Proof • We bound each term : 41

Proof • Bound From Below : – No error on tth round – Error on tth round • Cumulative bound : 42

Proof • Putting both bounds together : • We use first degree of freedom (and scale) : • Bound : 43

Proof • General Bound: • Choose: • Simple Bound: 44 Objective of SVM

Proof • Better bound : optimize the value of 45

Remarks • Bound does not depend on dimension of the feature vector • The bound holds for all sequences. It is not tight for most real world data • But, there exists a setting for which it is tight 46
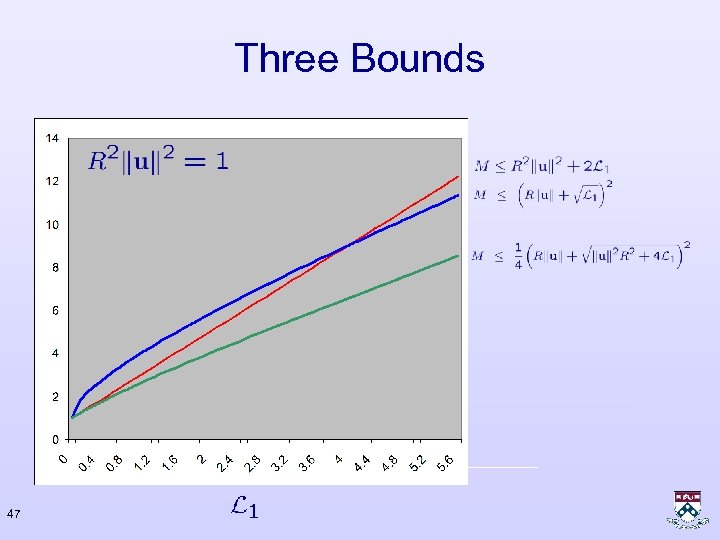
Three Bounds 47

Separable Case • Assume there exists such that for all examples Then all bounds are equivalent • Perceptron makes finite number of mistakes until convergence (not necessarily to ) 48

Separable Case – Other Quantities • Use 1 st (parameterization) degree of freedom • Scale the such that • Define • The bound becomes 49

Separable Case - Illustration 50

separable Case – Illustration Finding a separating hyperplance is more difficult 51 The Perceptron will make more mistakes

Inseparable Case • Difficult problem implies a large value of • In this case the Perceptron will make a large number of mistakes 52

Perceptron Algorithm • Extremely easy to • Quantities in bound are implement not compatible : no. of mistakes vs. hinge-loss. • Relative loss bounds for • Margin of examples is separable and ignored by update inseparable cases. Minimal assumptions • Same update for (not iid) separable case and • Easy to convert to a inseparable case. well-performing batch algorithm (under iid assumptions) 53

Passive – Aggressive Approach • The basis for a well-known algorithm in convex optimization due to Hildreth (1957) – Asymptotic analysis – Does not work in the inseparable case • Three versions : – PA-I separable case PA-II inseparable case • Beyond classification – Regression, one class, structured learning • Relative loss bounds 54

Motivation • Perceptron: No guaranties of margin after the update • PA : Enforce a minimal non-zero margin after the update • In particular : – If the margin is large enough (1), then do nothing – If the margin is less then unit, update such that the margin after the update is enforced to be unit 55

Input Space 56

Input Space vs. Version Space • Input Space : – Points are input data – One constraint is induced by weight vector – Primal space – Half space = all input examples that are classified correctly by a given predictor (weight vector) 57 • Version Space : – Points are weight vectors – One constraints is induced by input data – Dual space – Half space = all predictors (weight vectors) that classify correctly a given input example

Weight Vector (Version) Space The algorithm forces to reside in this region 58

Passive Step Nothing to do. already resides on the 59 desired side.
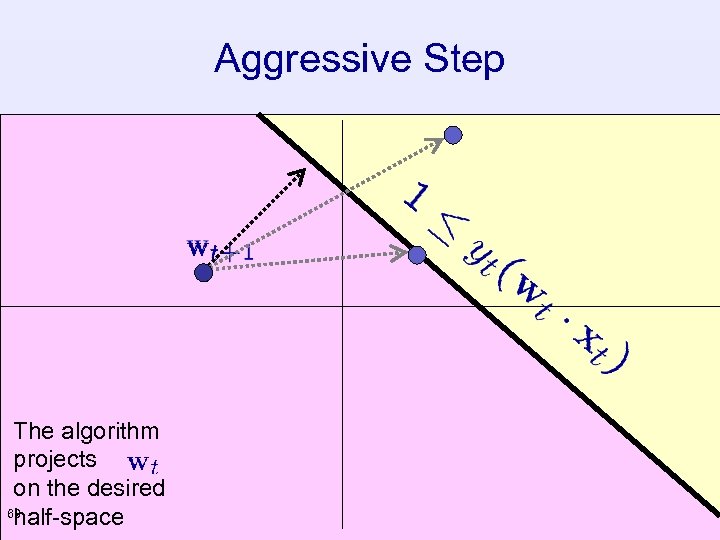
Aggressive Step The algorithm projects on the desired 60 half-space

Aggressive Update Step • Set to be the solution of the following optimization problem : • The Lagrangian: • Solve for the dual: 61

Aggressive Update Step • Optimize for : • Set the derivative to zero • Substitute back into the Lagrangian: • Dual optimization problem 62

Aggressive Update Step • Dual Problem: • Solve it: • What about the constraint? 63

Alternative Derivation • Additional Constraint (linear update: ( • Force the constraint to hold as equality • Solve: 64

Passive-Aggressive Update 65

Perceptron vs. PA • Common Update: • Perceptron • Passive-Aggressive 66
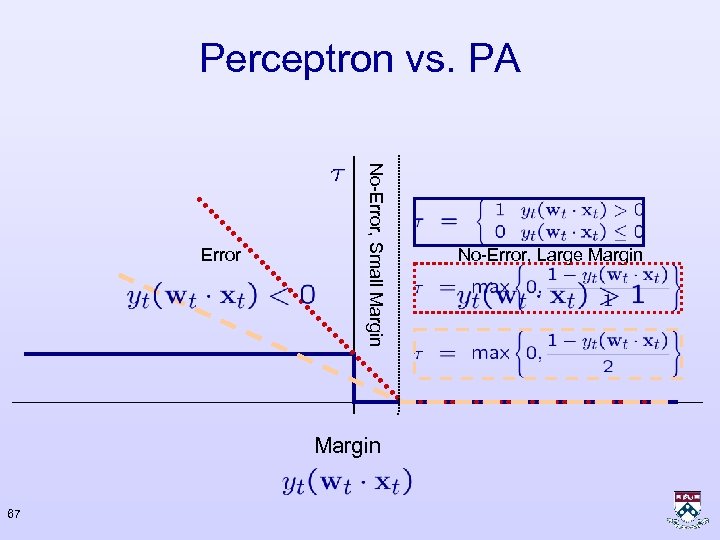
Perceptron vs. PA No-Error, Small Margin Error Margin 67 No-Error, Large Margin
Perceptron vs. PA 68
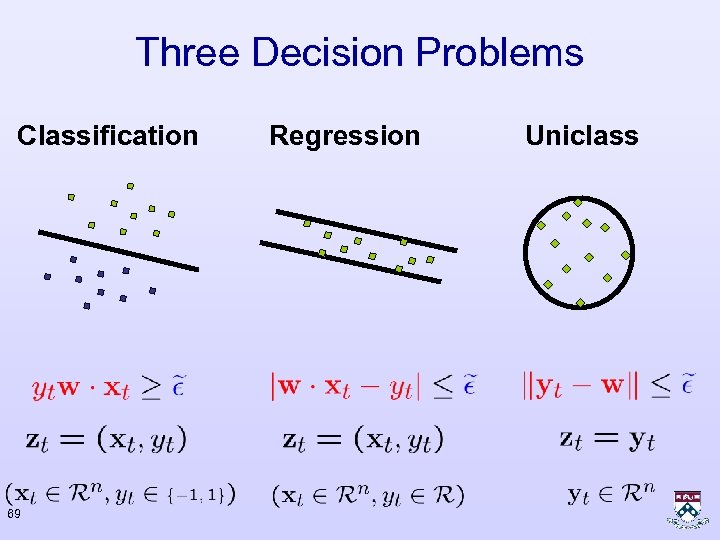
Three Decision Problems Classification 69 Regression Uniclass

The Passive-Aggressive Algorithm • Each example defines a set of consistent hypotheses: • The new vector is set to be the projection of onto Classification 70 Regression Uniclass

Loss Bound • Assume there exists • Assume: • Then: • Note: 71 such that
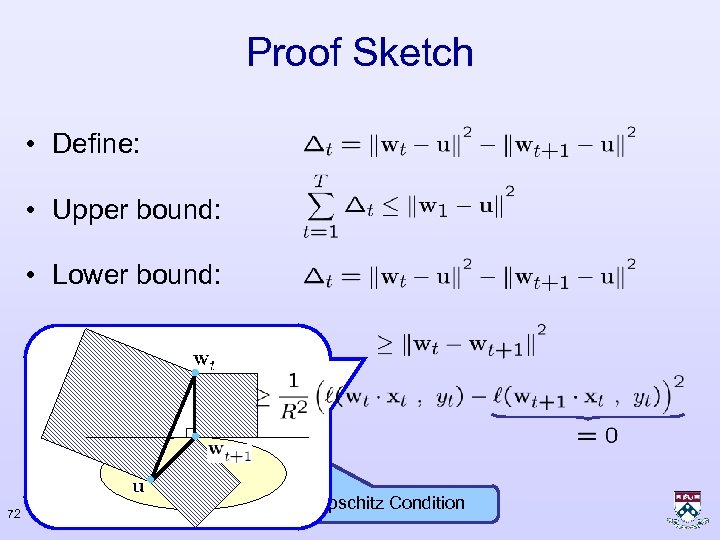
Proof Sketch • Define: • Upper bound: • Lower bound: 72 Lipschitz Condition
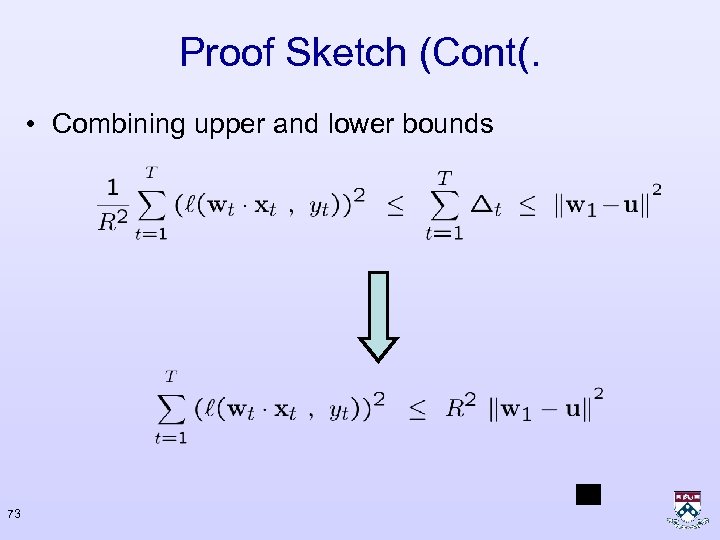
Proof Sketch (Cont(. • Combining upper and lower bounds 73

Unrealizable case There is no weight vector that satisfy all the constraints 74

Unrealizable Case 75

Unrealizable Case 76

Loss Bound for PA-I • Mistake bound: • Optimal value, set 77

Loss Bound for PA-II • Loss bound: • Similar proof technique as of PA • Bound can be improved similarly to the Perceptron 78

Four Algorithms Perceptron PA II PA 79

Four Algorithms Perceptron PA II PA 80

Next • Real-world problems – Examples – Commonalities – Extension of algorithms for the complex setting – Applications 81

Binary Classification If it’s not one class, It most be the other class 3 82 3

Multi Class Single Label Elimination of a single class is not enough 2 83 3 4 6

Ordinal Ranking / Regression Structure Over Possible Labels Viewer’s Rating Machine Prediction Order relation over labels 84
![Hierarchical Classification [DKS’ 04] Phonetic transcription of DECEMBER Gross error d ix CH eh Hierarchical Classification [DKS’ 04] Phonetic transcription of DECEMBER Gross error d ix CH eh](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-85.jpg)
Hierarchical Classification [DKS’ 04] Phonetic transcription of DECEMBER Gross error d ix CH eh m bcl b er Small errors d AE s eh m bcl b er d ix s eh NASAL bcl b er 85
![[DKS’ 04] Phonetic Hierarchy PHONEMES Sononorants Structure Over Possible Labels Silences Nasals Obstruents Liquids [DKS’ 04] Phonetic Hierarchy PHONEMES Sononorants Structure Over Possible Labels Silences Nasals Obstruents Liquids](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-86.jpg)
[DKS’ 04] Phonetic Hierarchy PHONEMES Sononorants Structure Over Possible Labels Silences Nasals Obstruents Liquids l y w r Vowels Front oyow uhuw 86 n m ng Affricates Plosives Center aa ao er aw ay Back iy ih ey eh ae b g d k p t jh ch Fricatives f v sh s th dh zh z

Multi-Class Multi-Label Document Full topic ranking The higher minimum wage signed into law… will be welcome relief for millions of workers …. The 90 cent-an-hour increase …. Relevant topics • REGULATION / POLICY • CORPORATE / INDUSTRIAL • LABOUR • GOVERNMENT / SOCIAL 87 • MARKETS • ECONOMICS • • • • • ECONOMICS CORPORATE / INDUSTRIAL REGULATION / POLICY MARKETS LABOUR GOVERNMENT / SOCIAL LEGAL/JUDICIAL REGULATION/POLICY SHARE LISTINGS PERFORMANCE ACCOUNTS/EARNINGS COMMENT / FORECASTS SHARE CAPITAL BONDS / DEBT ISSUES LOANS / CREDITS STRATEGY / PLANS INSOLVENCY / LIQUIDITY

Multi-Class Multi-Label Document Full topic ranking The higher minimum wage signed into law… will be welcome relief for millions of workers …. The 90 cent-an-hour increase …. • • • • • ECONOMICS INSOLVENCY / LIQUIDITY CORPORATE / INDUSTRIAL REGULATION / POLICY COMMENT / FORECASTS LABOUR LOANS / CREDITS LEGAL/JUDICIAL REGULATION/POLICY SHARE LISTINGS GOVERNMENT / SOCIAL PERFORMANCE ACCOUNTS/EARNINGS MARKETS SHARE CAPITAL BONDS / DEBT ISSUES STRATEGY / PLANS Non-trivial Evaluation Measures Relevant topics • REGULATION / POLICY • MARKETS • CORPORATE / INDUSTRIAL • LABOUR • GOVERNMENT / SOCIAL • ECONOMICS Recall Precision Any Error? No. Errors? 88

Noun Phrase Chunking Estimated volume was a light 2. 4 million ounces. Simultaneous Labeling 89

Named Entity Extraction Bill Clinton and Microsoft founder Bill Interactive Decisions Gates met today for 20 minutes. 90
![[Mc. Donald 06] Sentence Compression • The Reverse Engineer Tool is available now and [Mc. Donald 06] Sentence Compression • The Reverse Engineer Tool is available now and](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-91.jpg)
[Mc. Donald 06] Sentence Compression • The Reverse Engineer Tool is available now and is priced on a site-licensing basis , ranging from $8, 000 for a single user to $90, 000 for a multiuser project site. Complex Input – Output Relation • Essentially , design recovery tools read existing code and translate it into the language in which CASE is conversant -- definitions and structured diagrams. 91

Dependency Parsing John hit the ball with the bat Non-trivial Output 92
![[Shalev-Shwartz, Keshet, Singer 2004] Aligning Polyphonic Music Two ways for representing music Symbolic representation: [Shalev-Shwartz, Keshet, Singer 2004] Aligning Polyphonic Music Two ways for representing music Symbolic representation:](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-93.jpg)
[Shalev-Shwartz, Keshet, Singer 2004] Aligning Polyphonic Music Two ways for representing music Symbolic representation: Acoustic representation: 93
![[Shalev-Shwartz, Keshet, Singer 2004] Symbolic Representation symbolic representation: - pitch 94 - start-time [Shalev-Shwartz, Keshet, Singer 2004] Symbolic Representation symbolic representation: - pitch 94 - start-time](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-94.jpg)
[Shalev-Shwartz, Keshet, Singer 2004] Symbolic Representation symbolic representation: - pitch 94 - start-time
![[Shalev-Shwartz, Keshet, Singer 2004] Acoustic Representation acoustic signal: Feature Extraction (e. g. Spectral Analysis) [Shalev-Shwartz, Keshet, Singer 2004] Acoustic Representation acoustic signal: Feature Extraction (e. g. Spectral Analysis)](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-95.jpg)
[Shalev-Shwartz, Keshet, Singer 2004] Acoustic Representation acoustic signal: Feature Extraction (e. g. Spectral Analysis) 95 acoustic representation:
![[Shalev-Shwartz, Keshet, Singer 2004] The Alignment Problem Setting pitch time 96 actual start-time: [Shalev-Shwartz, Keshet, Singer 2004] The Alignment Problem Setting pitch time 96 actual start-time:](https://present5.com/presentation/f33c39e37fa956517d96906e530573fc/image-96.jpg)
[Shalev-Shwartz, Keshet, Singer 2004] The Alignment Problem Setting pitch time 96 actual start-time:

Challenges • Elimination is not enough • Structure over possible labels • Non-trivial loss functions • Complex input – output relation • Non-trivial output 97
Challenges • Interactive Decisions Fake News Show Fake News • A wide range of sequence features • Computing an answer is relatively costly 98 Show

Analysis as Labeling Model • Label gives role for corresponding input • "Many to one relation” • Still, not general enough 99

Examples Estimated volume was a light 2. 4 million ounces. B I O B I I O Bill Clinton and Microsoft founder Bill B-PER I-PER O B-ORG O B-PER Gates met today for 20 minutes. I-PER O O O 100

Outline of Solution • A quantitative evaluation of all predictions – Loss Function (application dependent) • Models class – set of all labeling functions – Generalize linear classification – Representation • Learning algorithm – Extension of Perceptron – Extension of Passive-Aggressive 101

Loss Functions • Hamming Distance (Number of wrong decisions) Estimated volume was a light 2. 4 million ounces. B I O B I I O B O O O B I I O O • Levenshtein Distance (Edit distance) – Speech • Number of words with incorrect parent – Dependency parsing 102

Outline of Solution • A quantitative evaluation of all predictions – Loss Function (application dependent) • Models class – set of all labeling functions – Generalize linear classification – Representation • Learning algorithm – Extension of Perceptron – Extension of Passive-Aggressive 103

Multiclass Representation I • k Prototypes 104

Multiclass Representation I • k Prototypes • New instance 105

Multiclass Representation I • k Prototypes • New instance • Compute Class r 1 2 1. 66 3 0. 37 4 106 -1. 08 -2. 09

Multiclass Representation I • k Prototypes • New instance • Compute Class r 1 -1. 08 2 1. 66 3 0. 37 4 -2. 09 • Prediction: The class achieving the highest Score 107

Multiclass Representation II • Map all input and labels into a joint vector space F Estimated volume was a light 2. 4 million ounces. B I O B I I O = (0 1 1 0 … ) • Score labels by projecting the corresponding feature vector 108

Multiclass Representation II • Predict label with highest score (Inference) • Naïve search is expensive if the set of possible labels is large Estimated volume was a light 2. 4 million ounces. B I O B I – No. of labelings = 3 No. of words 109 I I I O

Multiclass Representation II • Features based on local domains F Estimated volume was a light 2. 4 million ounces. B I O B I I O • Efficient Viterbi decoding for sequences 110 = (0 1 1 0 … )

Multiclass Representation II After Shalev Correct Labeling Almost Correct Labeling 111

Multiclass Representation II After Shalev Correct Labeling Incorrect Labeling Worst Labeling 112 Almost Correct Labeling

Multiclass Representation II After Shalev Correct Labeling Almost Correct Labeling Worst Labeling 113

Multiclass Representation II After Shalev Correct Labeling Almost Correct Labeling Worst Labeling 114

Two Representations • Weight-vector per class (Representation I) – Intuitive – Improved algorithms • Single weight-vector (Representation II) – Generalizes representation I F(x, 4)= 0 0 0 x 0 – Allows complex interactions between input and output 115

Why linear models? • Combine the best of generative and classification models: – Trade off labeling decisions at different positions – Allow overlapping features • Modular – factored scoring – loss function – From features to kernels 116

Outline of Solution • A quantitative evaluation of all predictions – Loss Function (application dependent) • Models class – set of all labeling functions – Generalize linear classification – Representation • Learning algorithm – Extension of Perceptron – Extension of Passive-Aggressive 117

Multiclass Multilabel Perceptron Single Round • Get a new instance • Predict ranking • Get feedback • Compute loss • If 118 update weight-vectors

Multiclass Multilabel Perceptron Update (1) • Construct Error-Set • Form any set of parameters § § If § 119 then that satisfies:

Multiclass Multilabel Perceptron Update (1) 120

Multiclass Multilabel Perceptron Update (1) 1 2 3 121 4 5

Multiclass Multilabel Perceptron Update (1) 1 2 3 122 4 5

Multiclass Multilabel Perceptron Update (1) 1 2 3 123 4 5 0 0

Multiclass Multilabel Perceptron Update (1) 1 5 2 0 0 0 3 124 4 a 0 1 -a

Multiclass Multilabel Perceptron Update (2) • Set for • Update: 125
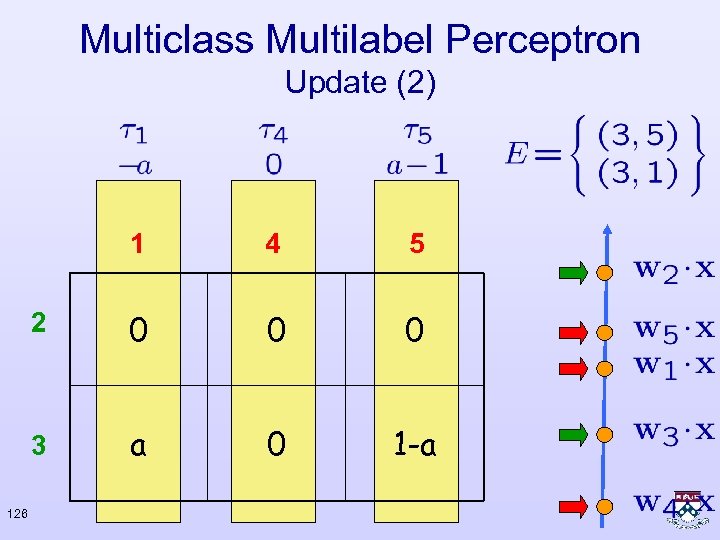
Multiclass Multilabel Perceptron Update (2) 1 5 2 0 0 0 3 126 4 a 0 1 -a

Multiclass Multilabel Perceptron Update (2) 1 5 2 0 0 0 3 127 4 a 0 1 -a

Uniform Update 1 5 2 0 0 0 3 128 4 1/2 0 1/2

Max Update • Sparse • Performance is worse than Uniform’s 1 5 2 0 0 0 3 129 4 0 0 1
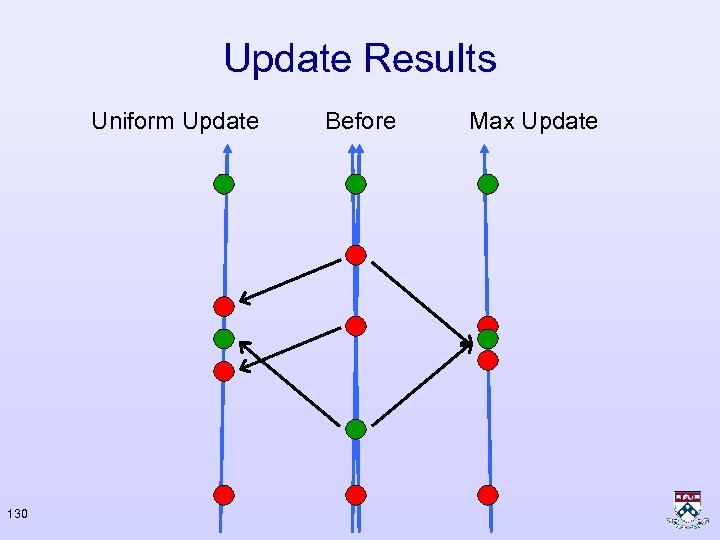
Update Results Uniform Update 130 Before Max Update

Margin for Multi Class • Binary: • Multi Class: Prediction Margin Error 131

Margin for Multi Class • Binary: • Multi Class: 132

Margin for Multi Class • Multi Class: Because the loss But not all mistakes How do you know? function is not are equal? constant ! 133

Margin for Multi Class • Multi Class: So, use it ! 134

Linear Structure Models After Shalev Correct Labeling Almost Correct Labeling 135

Linear Structure Models After Shalev Correct Labeling Incorrect Labeling Worst Labeling 136 Almost Correct Labeling
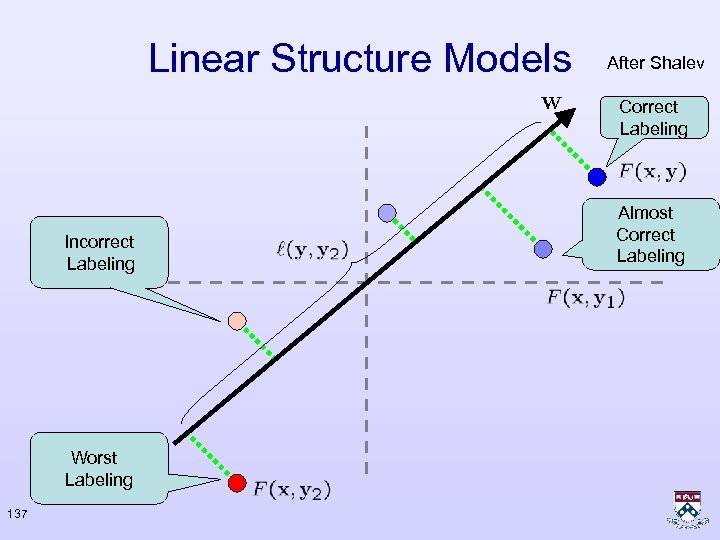
Linear Structure Models After Shalev Correct Labeling Incorrect Labeling Worst Labeling 137 Almost Correct Labeling
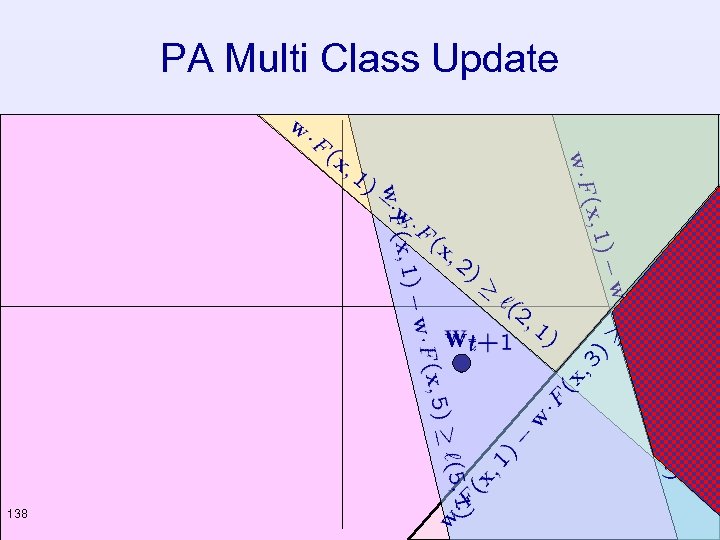
PA Multi Class Update 138

PA Multi Class Update • Project the current weight vector such that the instance ranking is consistent with loss function • Set to be the solution of the following optimization problem : 139

PA Multi Class Update • Problem – intersection of constraints may be empty • Solutions – Does not occur in practice – Add a slack variable – Remove constraints 140

Add a Slack Variable • Add a slack variable: Generalized Hinge Loss • Rewrite the optimization: 141

Add a Slack Variable Estimated volume was a light 2. 4 million ounces. • We like to Isolve : B I B O I I I O • May have exponential number of constraints, thus intractable – If the loss can be factored then there is a polynomial equivalent set of constraints (Taskar et. al 2003) – Remove constraints (the other solution for the emptyset problem) 142

PA Multi Class Update • Remove constraints : • How to choose the single competing labeling ? – The labeling that attains the highest score! 143 – … which is the predicted label according to the current model

PA Multiclass online algorithm • Initialize • For – – – 144 Receive an input instance Outputs a prediction Receives a feedback label Computes loss Update the prediction rule

Advantages • • • Process one training instance at a time Very simple Predictable runtime, small memory Adaptable to different loss functions Requires : – Inference procedure – Loss function – Features 145

Batch Setting • Often we are given two sets : – Training set used to find a good model – Test set for evaluation • Enumerate over the training set – Possibly more than once – Fix the weight vector • Evaluate on Test Set • Formal guaranties if training set and test set are i. i. d from fixed (unknown) distribution 146

Two Improvements • Averaging – Instead of using final weight-vector use a combination of all weight-vector obtained during training time • Top – k update – Instead of using only the labeling with highest score, the k labelings with highest score 147

Averaging • Initialize • For – – – Receive an input instance Outputs a prediction Receives a feedback label Computes loss Update the prediction rule – Update the average rule 148 MIRA

Top-k Update • Recall : – Inference : – Update 149

Top-K Update • Recall : – Inference – Top-k Inference 150

Top-K Update • Top-k Inference: • Update: 151

Previous Approaches • Focus on sequences • Similar constructions for other structures • Mainly batch algorithms 152

Previous Approaches • Generative models: probabilistic generators of sequence-structure pairs – Hidden Markov Models (HMMs) – Probabilistic CFGs • Sequential classification: decompose structure assignment into a sequence of structural decisions • Conditional models : probabilistic model of labels given input – Conditional Random Fields [LMR 2001] 153

Previous Approaches • Re-ranking : Combine generative and discriminative models – Full parsing [Collins 2000] • Max Margin Makrov Networks [TGK 2003] – Use all competing labels – Elegant factorization – Closely related to PA with all the constraints 154

HMMs y 1 x 1 a x 2 a x 1 b y 3 x 3 a x 2 b x 1 c 155 y 2 x 3 b x 2 c x 3 c
HMM 156

HMMs • Solves a more general problem then required. Models the joint probability. • Hard to model overlapping features, yet application needs richer input representation. – E. g. word identity, capitalization, ends in “-tion” , word in word list, word font, white space ratio, begins with number, word font ends with “? ” • Relax conditional independence of features on labels intractability 157

John Lafferty, Andrew Mc. Callum, Fernando Pereira 2001 Conditional Random Fields • Define distributions over labels • Maximize the log-likelihood of data 158 • Dynamic programming for expectations (forward-backward algorithm) • Standard convex optimization (L-BFGS)

Local Classifiers Dan Roth MEMM • Train local classifiers. – E. g. Estimated volume was a light 2. 4 million ounces. B ? O B I I O • Combine results in test time • Cheap to train • Can not model well long distance interactions – MEMMs, local classifiers – Combine classifiers at test time – Problem: Can not trade-off decisions at different locations (labelbias problem) 159

Michael Collins 2000 Re-Ranking • Use a generative model to reduce exponential number of labelings into a polynomial number of candidates – Local features • Use the Perceptron algorithm to re-rank the list – Global features • Great results! 160

Empirical Evaluation • • 161 Category Ranking / Multiclass multilabel Noun Phrase Chunking Named entities Dependency Parsing Genefinder Phoneme Alignment Non-projective Parsing

Experimental Setup • Algorithms : – Rocchio, normalized prototypes – Perceptron, one per topic – Multiclass Perceptron - Is. Err, Error. Set. Size • Features – About 100 terms/words per category • Online to Batch : – Cycle once through training set – Apply resulting weight-vector to the test set 162

Data Sets Reuters 21578 Training Examples Test Examples Topics < Topics / Example > No. Features 163 8, 631 2, 158 90 1. 24 3, 468
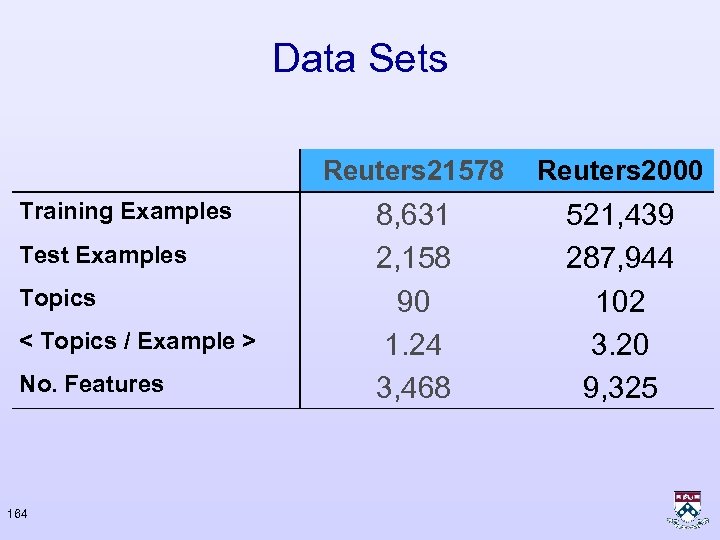
Data Sets Reuters 21578 Training Examples Test Examples Topics < Topics / Example > No. Features 164 Reuters 2000 8, 631 2, 158 90 1. 24 3, 468 521, 439 287, 944 102 3. 20 9, 325
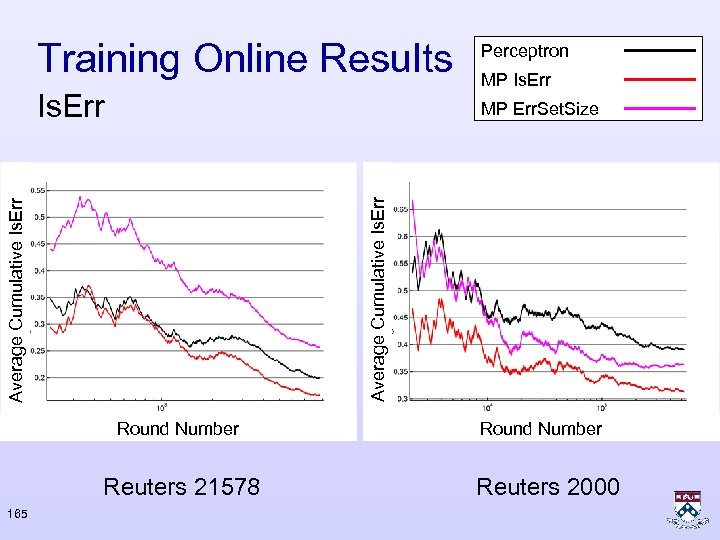
Training Online Results Perceptron Is. Err MP Err. Set. Size Average Cumulative Is. Err Round Number Reuters 21578 165 MP Is. Err Round Number Reuters 2000
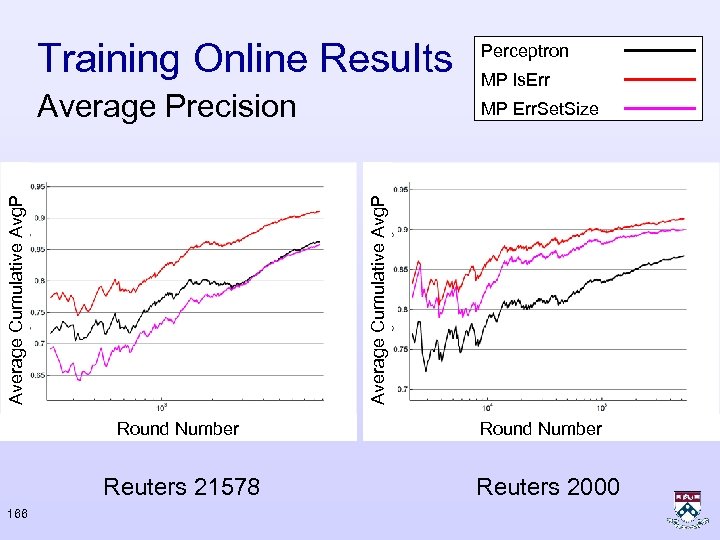
Perceptron Average Precision MP Err. Set. Size Round Number Reuters 21578 166 MP ls. Err Average Cumulative Avg. P Training Online Results Round Number Reuters 2000
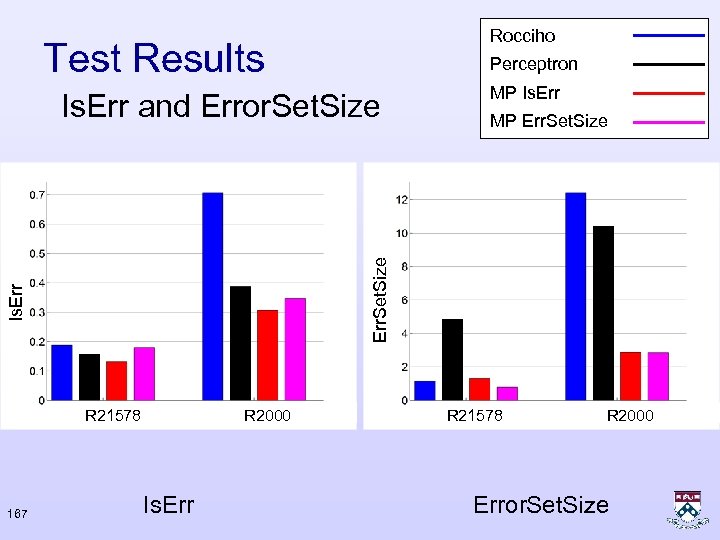
Rocciho Test Results Perceptron Is. Err R 21578 167 MP Err. Set. Size Is. Err and Error. Set. Size MP Is. Err R 2000 Is. Err R 21578 R 2000 Error. Set. Size

Sequence Text Analysis • Features : – Meaningful word features – POS features – Unigram and bi-gram NER/NP features F Estimated volume was a light 2. 4 million ounces. B I O B I I O = (0 1 1 0 … ) • Inference : – Dynamic programming – Linear in length, quadratic in number of classes 168

Noun Phrase Chunking Mc. Donald, Crammer, Pereira Estimated volume was a light 2. 4 million ounces. Avg. Perceptron CRF 0. 942 MIRA 169 0. 941 0. 943

Noun Phrase Chunking Performance on test data Mc. Donald, Crammer, Pereira 170 Training time in CPU minutes

Named Entity Extraction Mc. Donald, Crammer, Pereira Bill Clinton and Microsoft founder Bill Gates met today for 20 minutes. Avg. Perceptron CRF 0. 830 MIRA 171 0. 823 0. 831
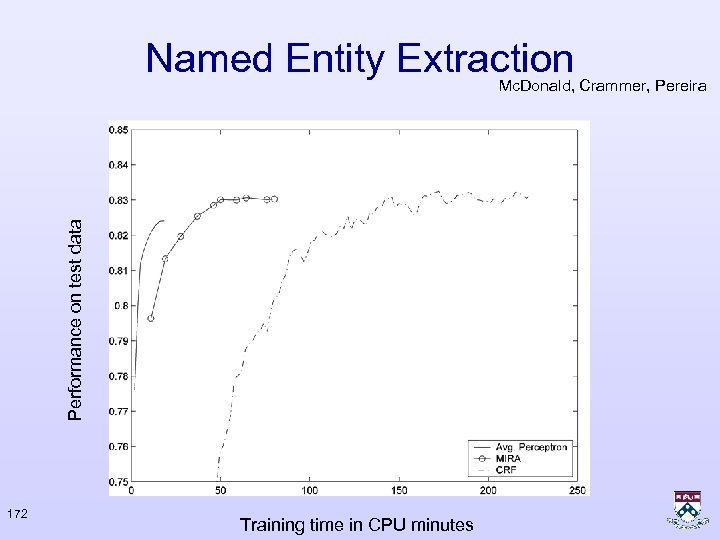
Named Entity Extraction Performance on test data Mc. Donald, Crammer, Pereira 172 Training time in CPU minutes

Dependency parsing • Features : – Anything over words – single edges • Inference : – Search over possible trees in cubic time (Eisner, Satta) 173
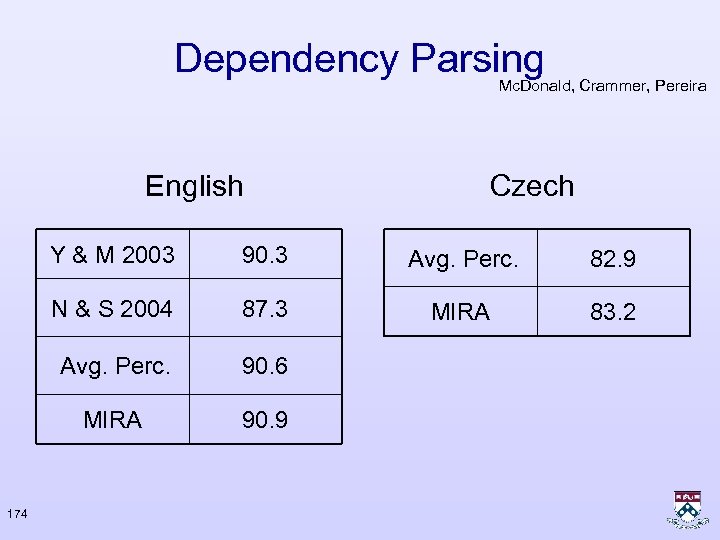
Dependency Parsing Mc. Donald, Crammer, Pereira English Czech Y & M 2003 Avg. Perc. 82. 9 N & S 2004 87. 3 MIRA 83. 2 Avg. Perc. 90. 6 MIRA 174 90. 3 90. 9

Gene Finding Bernal, Crammer, Hatzigeorgiu, Pereira • Semi-Markov Models (features includes segments length information( • Decoding quadratic in length of sequence specificity = FP / (FP + TN) sensitivity = FN / (TP + FN) 175

Dependency Parsing Mc. Donald & Pereira • Complications: – High order features and multiply parents per word – Non-projective trees • Approximate inference Czech 1 – proj 2 – proj 84. 2 1 – non-proj 176 83. 0 84. 1 2 – non-proj 85. 2

Phoneme Alignment Keshet, Shalev-Shwartz, Singer, Chazan • Input: Acoustic signal + true phonemes • Output : Segmentation of the signal t<10 t<30 t<40 Discriminative 79. 2 92. 1 96. 2 98. 1 Brugnara et al 177 t<20 75. 3 88. 9 94. 4 97. 1

Summary • Online training for complex decisions • Simple to implement, fast to train • Modular : – Loss function – Feature Engineering – Inference procedure • Works well in practice • Theoretically analyzed 178

Uncovered Topics • Kernels • Multiplicative updates • Bregman divergences and projections • Theory of online-to-batch • Matrix representations and updates 179

Partial Bibliography • Prediction, learning, and games. Nicolò Cesa-Bianchi and Gábor Lugosi • Y. Censor & S. A. Zenios, “Parallel Optimization”, Oxford UP, 1997 • Y. Freund & R. Schapire, “Large margin classification using the Perceptron algorithm”, MLJ, 1999. • M. Herbster, “Learning additive models online with fast evaluating kernels”, COLT 2001 • J. Kivinen, A. Smola, and R. C. Williamson, “Online learning with kernels”, IEEE Trans. on SP, 2004 • H. H. Bauschke & J. M. Borwein, “On Projection Algorithms for Solving Convex Feasibility Problems”, SIAM Review, 1996 180

Applications • • Online Passive Aggressive Algorithms, CDSS’ 03 + CDKSS’ 05 Online Ranking by Projecting, CS’ 05 Large Margin Hierarchical Classification, DKS’ 04 Online Learning of Approximate Dependency Parsing Algorithms. R. Mc. Donald and F. Pereira European Association for Computational Linguistics, 2006 • Discriminative Sentence Compression with Soft Syntactic Constraints. R. Mc. Donald. European Association for Computational Linguistics, 2006 • Non-Projective Dependency Parsing using Spanning Tree Algorithms. R. Mc. Donald, F. Pereira, K. Ribarov and J. Hajic HLTEMNLP, 2005 • Flexible Text Segmentation with Structured Multilabel Classification. R. Mc. Donald, K. Crammer and F. Pereira HLT-EMNLP, 2005 181

Applications • • • Online and Batch Learning of Pseudo-metrics, SSN’ 04 Learning to Align Polyphonic Music, SKS’ 04 The Power of Selective Memory: Self-Bounded Learning of Prediction Suffix Trees, DSS’ 04 First-Order Probabilistic Models for Coreference Resolution. Aron Culotta, Michael Wick, Robert Hall and Andrew Mc. Callum. NAACL/HLT, 2007 • Structured Models for Fine-to-Coarse Sentiment Analysis R. Mc. Donald, K. Hannan, T. Neylon, M. Wells, and J. Reynar Association for Computational Linguistics, 2007 • Multilingual Dependency Parsing with a Two-Stage Discriminative Parser. R. Mc. Donald and K. Lerman and F. Pereira Conference on Natural Language Learning, 2006 • Discriminative Kernel-Based Phoneme Sequence Recognition, Joseph Keshet, Shai Shalev-Shwartz, Samy Begio, Yoram Singer and Dan Chazan, International Conference on Spoken Language Processing , 2006 182

183
f33c39e37fa956517d96906e530573fc.ppt