On Top-n Reverse Top-k Queries Variants Algorithms and

On Top-n Reverse Top-k Queries: Variants, Algorithms, and Applications 陳良弼 Arbee L. P. Chen National Chengchi University 9/21/2012 at NCHU

IEEE International Conference on Data Engineering (ICDE) • A premium international conference on databases • Inaugural conference held at Los Angeles in 1984 • Held in Taiwan in 1995

ICDE 2012 Research Papers Distribution • System Aspects – Privacy and Security 8% – Storage Management and Performance 7% – Entity resolution/Versioning 7% – Query Processing 31% • • • Top-k query 9% Distributed/parallel/map-reduce 8% Location-aware 5% Execution Plan 5% Graph indexing 4%

• Text/Web/Keyword Search 19% • Stream/Trajectory/Sequence/Spatio-Temporal 10% • Social Media 7% • Uncertain Database 6% • Data Mining 5%

Efficient Dual-Resolution Layer Indexing for Top-k Queries, ICDE 2012 H 1 H 2 price 0. 55 0. 45 distance to the airport 0. 4 0. 6 service 0. 5 0. 4 H 9 0. 5 H 7 0. 1 H 2 H 6 H 8 H 4 H 9 H 5 H 3

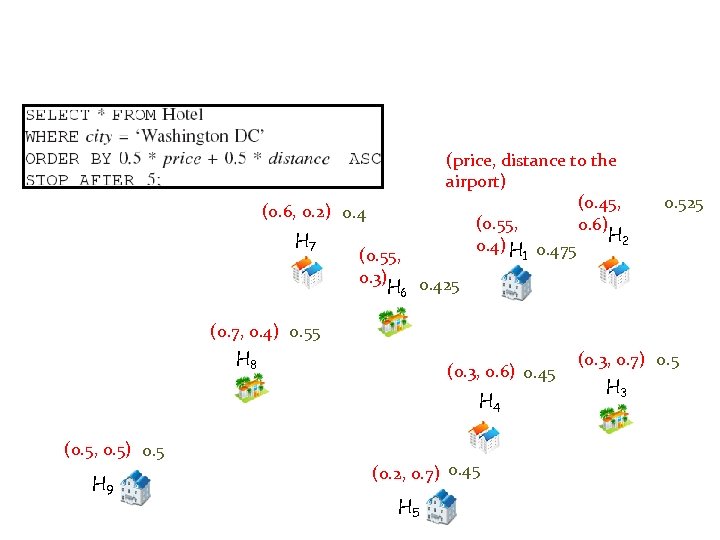(price, distance to the airport) (0. 45, (0. 55, 0. 6) H 2 0. 4) H 0. 475 1 (0. 6, 0. 2) 0. 4 H 7 0. 525 (0. 55, 0. 3) H 6 0. 425 (0. 7, 0. 4) 0. 55 H 8 (0. 3, 0. 6) 0. 45 H 4 (0. 5, 0. 5) 0. 5 H 9 (0. 2, 0. 7) 0. 45 H 5 (0. 3, 0. 7) 0. 5 H 3

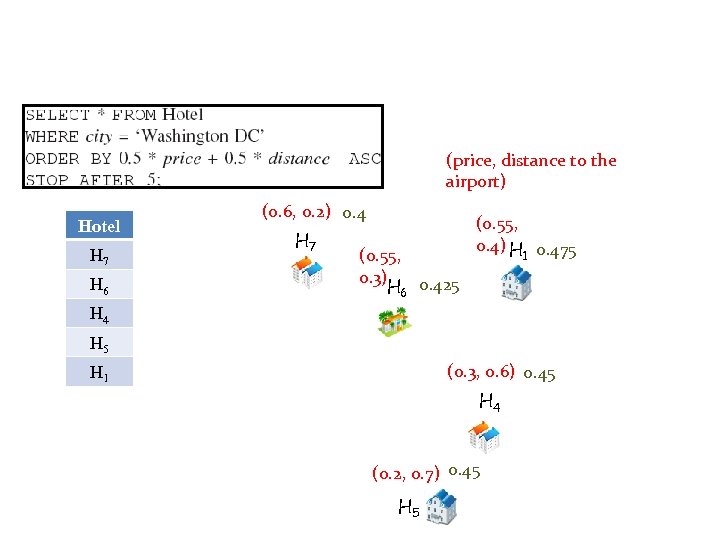(price, distance to the airport) Hotel H 7 H 6 (0. 6, 0. 2) 0. 4 H 7 (0. 55, 0. 3) H 6 0. 425 (0. 55, 0. 4) H 0. 475 1 H 4 H 5 (0. 3, 0. 6) 0. 45 H 1 H 4 (0. 2, 0. 7) 0. 45 H 5

Answering Why-not Questions on Top-k Queries, ICDE 2012 (Cleanliness, delicious, Parking spaces) • Top-k query Top-2(0. 4, 0. 5, 0. 1) p 3 (50, 90, 60) 71 p 2 (70, 20, 30) 41 p 4 (75, 70, 50) 70 p 6 (58, 20, 30) 36. 2 p 1 (95, 80, 40) 82 p 5 (85, 60) 69

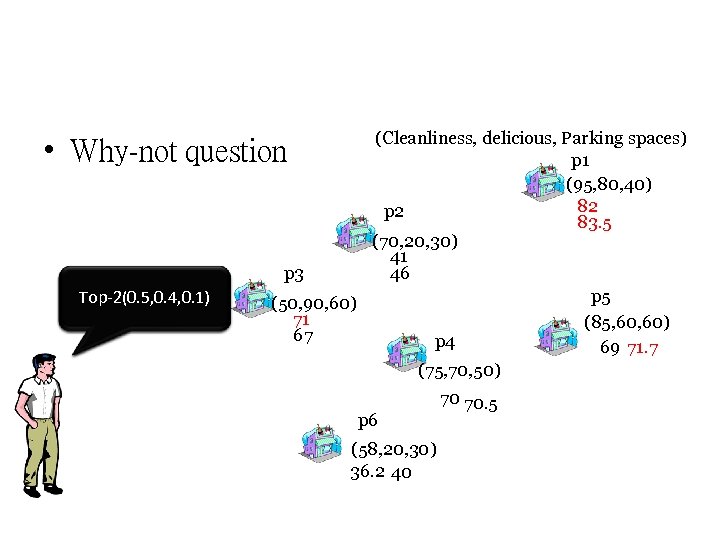(Cleanliness, delicious, Parking spaces) p 1 (95, 80, 40) 82 p 2 83. 5 (70, 20, 30) 41 p 3 46 p 5 (50, 90, 60) 71 (85, 60) 67 p 4 69 71. 7 (75, 70, 50) • Why-not question Should I revise my Why p 5 change my Should I is not in my Top-2(0. 5, 0. 4, 0. 1) p 5 does not exist? query to look for top-2 query list? weights? top-5 hotels? p 6 (58, 20, 30) 36. 2 40 70 70. 5

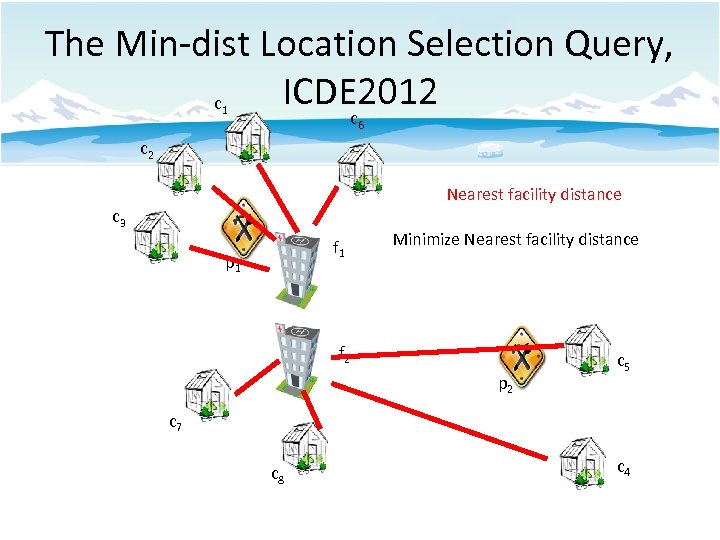The Min-dist Location Selection Query, ICDE 2012 c 1 c 6 c 2 Nearest facility distance c 3 f 1 p 1 Minimize Nearest facility distance f 2 p 2 c 5 c 7 c 8 c 4

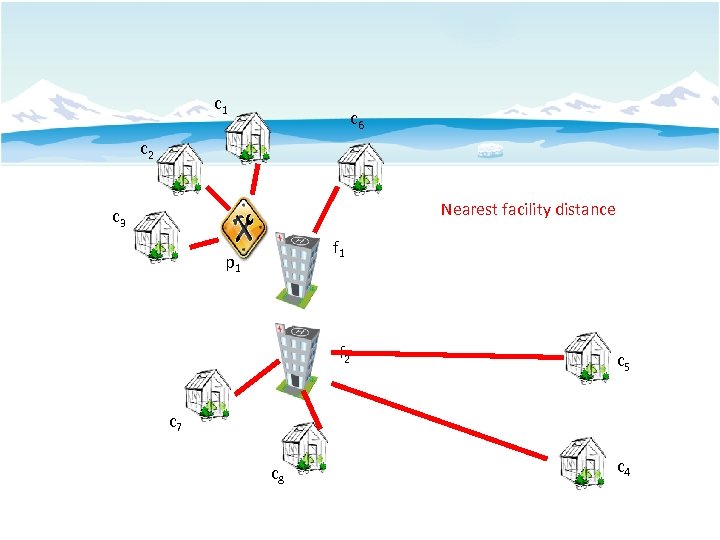c 1 c 6 c 2 Nearest facility distance c 3 f 1 p 1 f 2 c 5 c 7 c 8 c 4

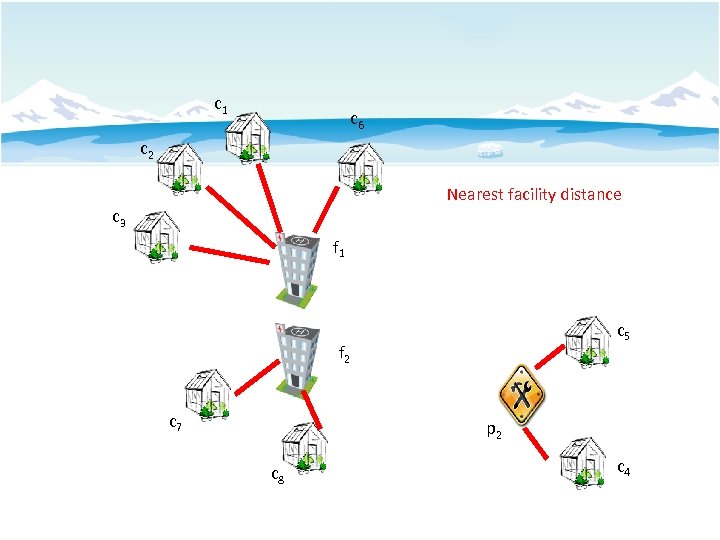c 1 c 6 c 2 Nearest facility distance c 3 f 1 c 5 f 2 c 7 p 2 c 8 c 4

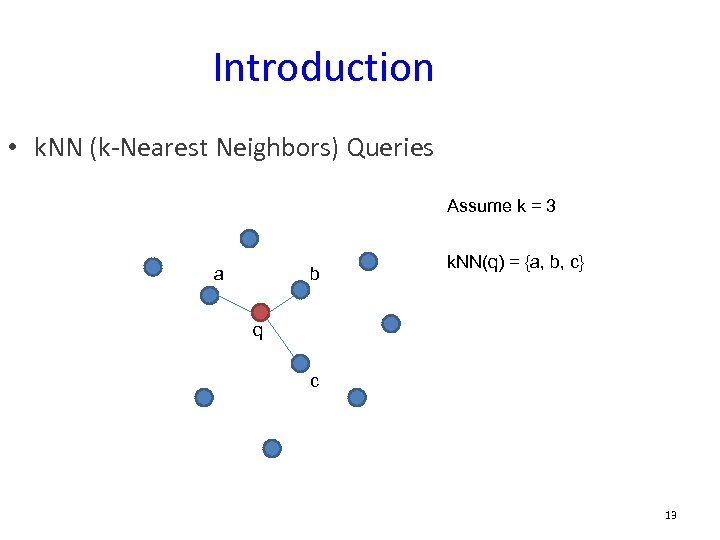Introduction • k. NN (k-Nearest Neighbors) Queries Assume k = 3 a b k. NN(q) = {a, b, c} q c 13

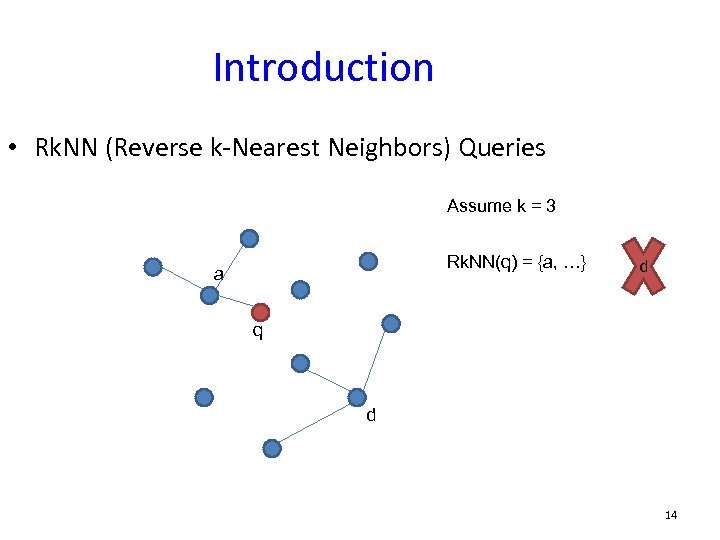Introduction • Rk. NN (Reverse k-Nearest Neighbors) Queries Assume k = 3 Rk. NN(q) = {a, …} a d q d 14

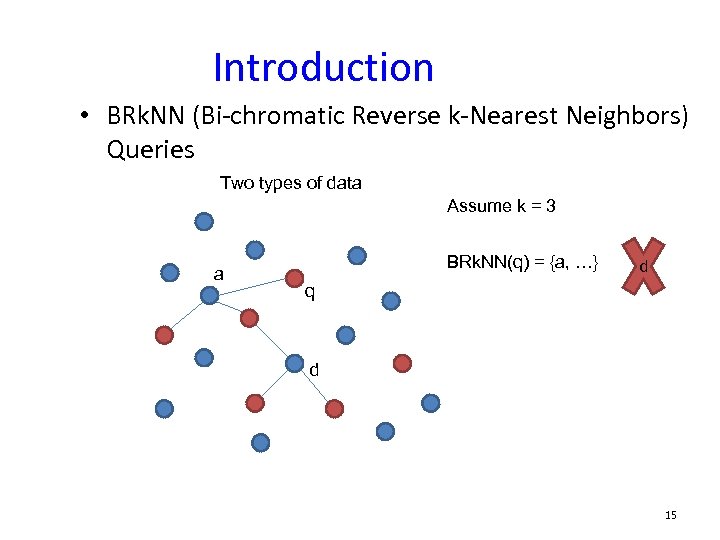Introduction • BRk. NN (Bi-chromatic Reverse k-Nearest Neighbors) Queries Two types of data Assume k = 3 a BRk. NN(q) = {a, …} d q d 15

Application I shop customer Which location is the best?

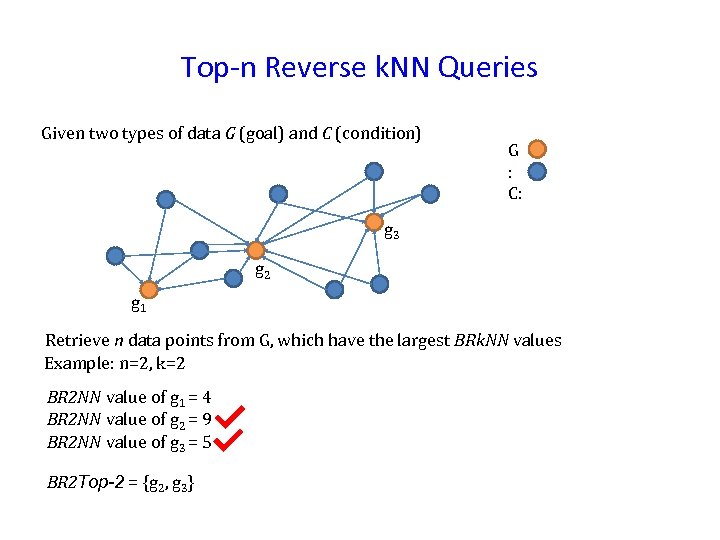Top-n Reverse k. NN Queries Given two types of data G (goal) and C (condition) G : C: g 3 g 2 g 1 Retrieve n data points from G, which have the largest BRk. NN values Example: n=2, k=2 BR 2 NN value of g 1 = 4 BR 2 NN value of g 2 = 9 BR 2 NN value of g 3 = 5 BR 2 Top-2 = {g 2, g 3}

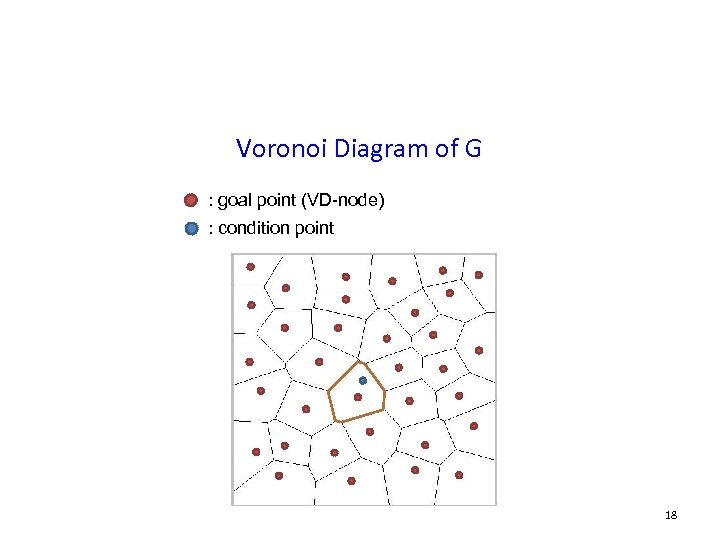Voronoi Diagram of G : goal point (VD-node) : condition point 18

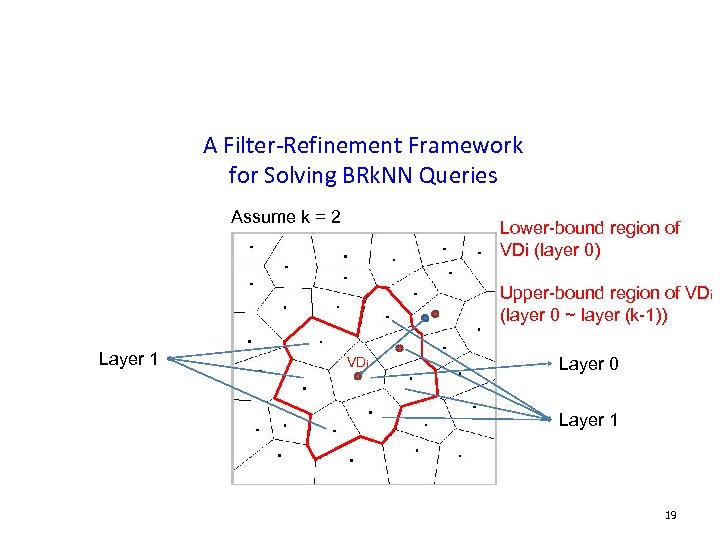A Filter-Refinement Framework for Solving BRk. NN Queries Assume k = 2 Lower-bound region of VDi (layer 0) Upper-bound region of VDi (layer 0 ~ layer (k-1)) Layer 1 VDi Layer 0 Layer 1 19

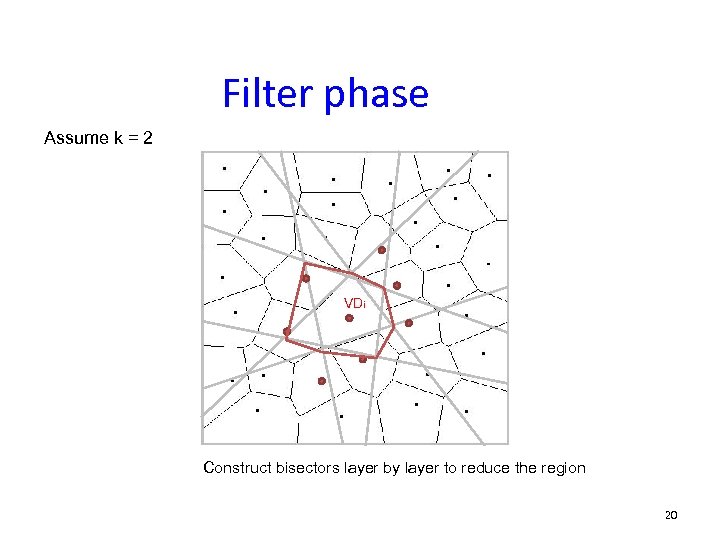Filter phase Assume k = 2 VDi Construct bisectors layer by layer to reduce the region 20

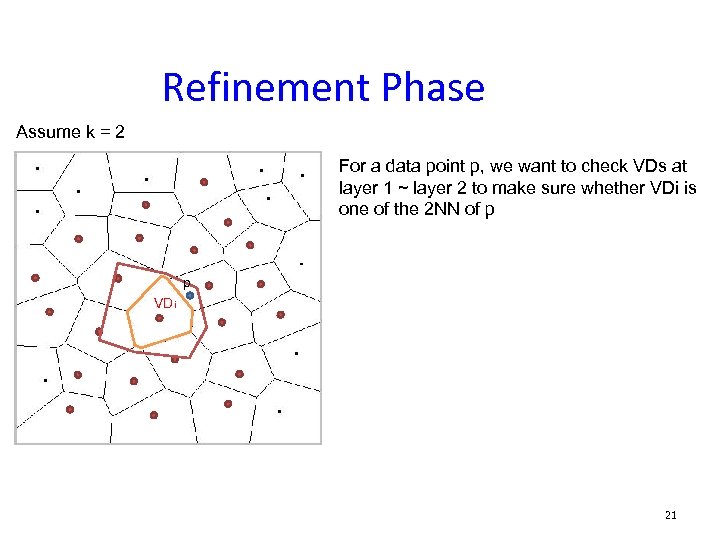Refinement Phase Assume k = 2 For a data point p, we want to check VDs at layer 1 ~ layer 2 to make sure whether VDi is one of the 2 NN of p p VDi 21

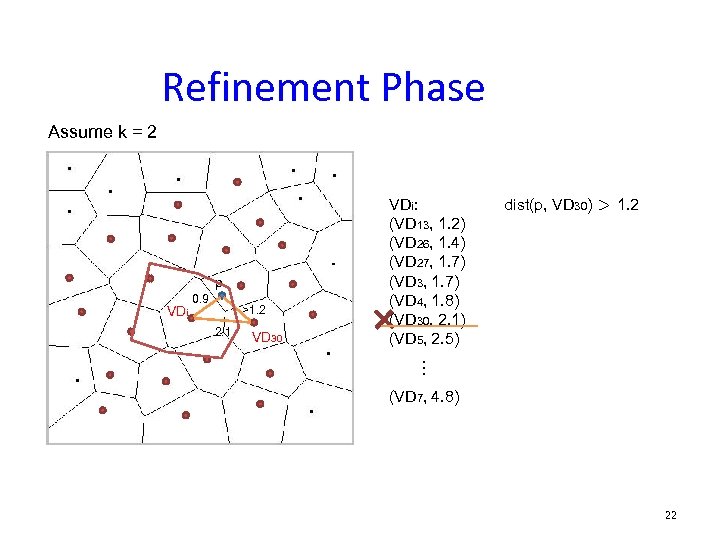Refinement Phase Assume k = 2 p VDi 0. 9 >1. 2 2. 1 VD 30 VDi: (VD 13, 1. 2) (VD 26, 1. 4) (VD 27, 1. 7) (VD 3, 1. 7) (VD 4, 1. 8) (VD 30, 2. 1) (VD 5, 2. 5) dist(p, VD 30) ＞ 1. 2 … (VD 7, 4. 8) 22

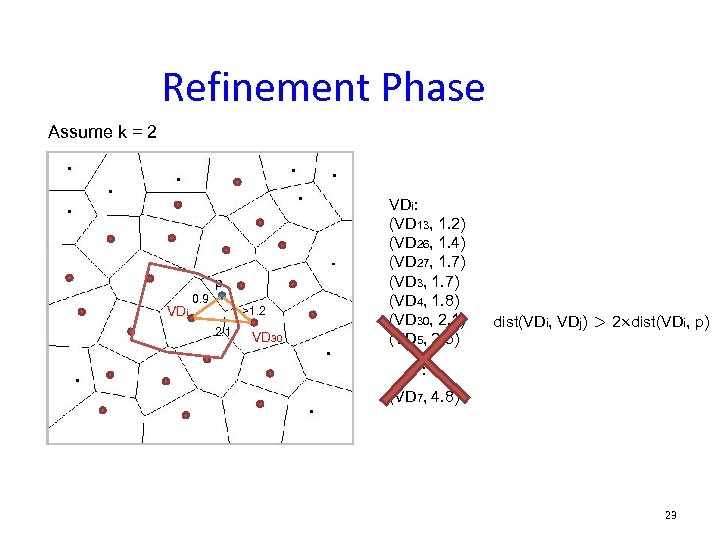Refinement Phase Assume k = 2 p VDi 0. 9 >1. 2 2. 1 VD 30 VDi: (VD 13, 1. 2) (VD 26, 1. 4) (VD 27, 1. 7) (VD 3, 1. 7) (VD 4, 1. 8) (VD 30, 2. 1) (VD 5, 2. 5) dist(VDi, VDj) ＞ 2 dist(VDi, p) … (VD 7, 4. 8) 23

Application II Maximum Coverage BRk. NN Queries Retrieve 2 points from dataset G Assume k = 2 24

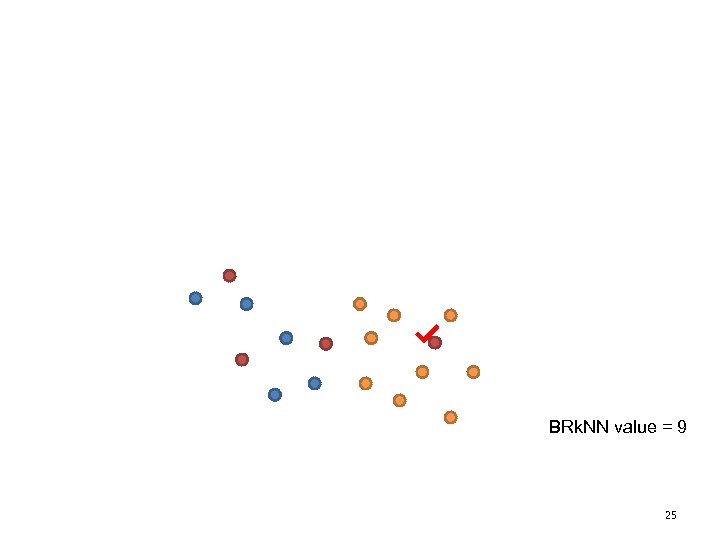BRk. NN value = 9 25

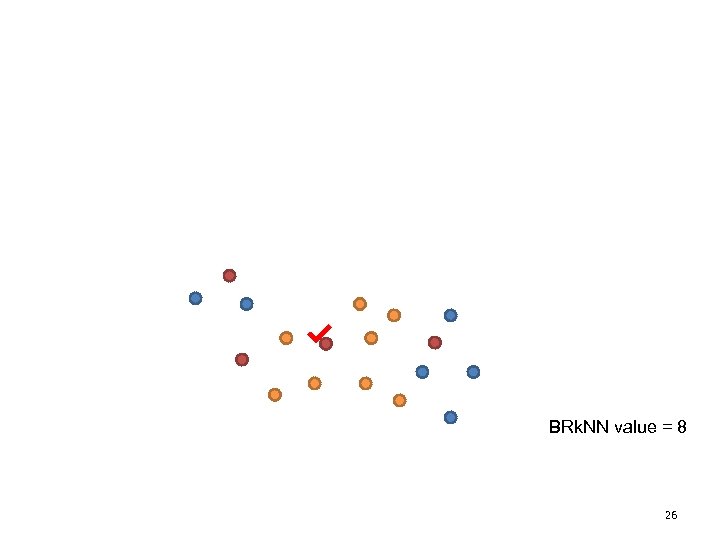BRk. NN value = 8 26

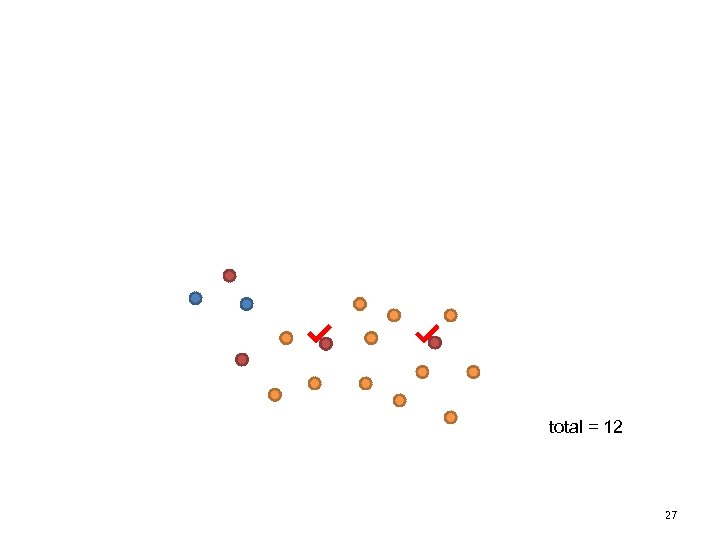total = 12 27

total = 14 28

Maximum Coverage BRk. NN Queries • Given: – A set of goal points (G) – A set of condition points (C) – k: the k value of BRk. NN C G • Goal: – Find n points from G, g 1, g 2, …, gn, which maximize |∪i=1~n. BRk. NN(gi, G, C)| 29

Application III • Find n Most Favorite Products based on Reverse Topk Queries

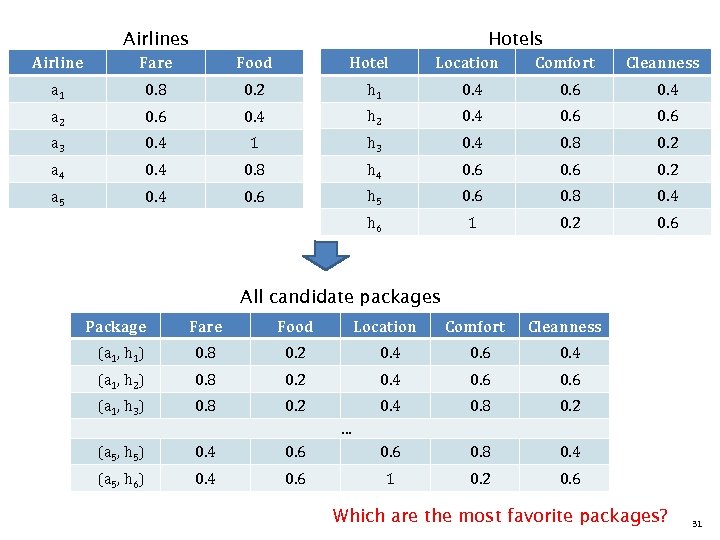Airlines Hotels Location Comfort Cleanness Airline Fare Food a 1 0. 8 0. 2 h 1 0. 4 0. 6 0. 4 a 2 0. 6 0. 4 h 2 0. 4 0. 6 a 3 0. 4 1 h 3 0. 4 0. 8 0. 2 a 4 0. 8 h 4 0. 6 0. 2 a 5 0. 4 0. 6 h 5 0. 6 0. 8 0. 4 h 6 1 0. 2 0. 6 All candidate packages Package Fare Food Location Comfort Cleanness (a 1, h 1) 0. 8 0. 2 0. 4 0. 6 0. 4 (a 1, h 2) 0. 8 0. 2 0. 4 0. 6 (a 1, h 3) 0. 8 0. 2 0. 4 0. 8 0. 2 … (a 5, h 5) 0. 4 0. 6 0. 8 0. 4 (a 5, h 6) 0. 4 0. 6 1 0. 2 0. 6 Which are the most favorite packages? 31

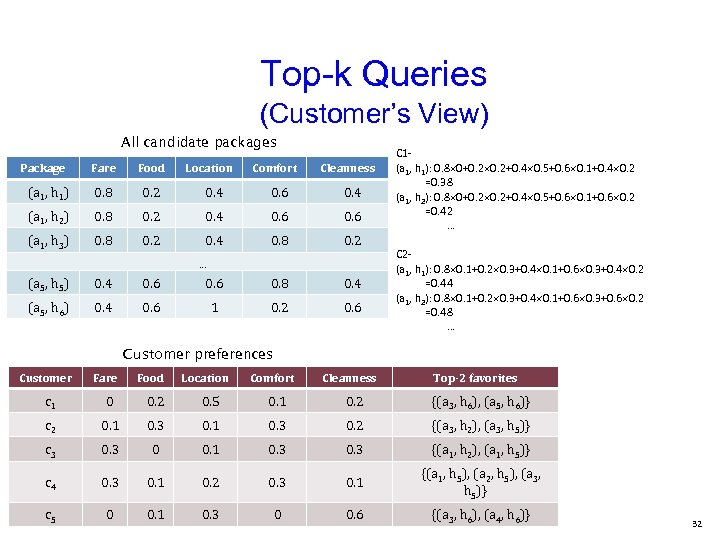Top-k Queries (Customer’s View) All candidate packages Package Fare Food Location Comfort Cleanness (a 1, h 1) 0. 8 0. 2 0. 4 0. 6 0. 4 (a 1, h 2) 0. 8 0. 2 0. 4 0. 6 (a 1, h 3) 0. 8 0. 2 0. 4 0. 8 0. 2 … (a 5, h 5) 0. 4 0. 6 0. 8 0. 4 (a 5, h 6) 0. 4 0. 6 1 0. 2 0. 6 C 1(a 1, h 1): 0. 8 0+0. 2+0. 4 0. 5+0. 6 0. 1+0. 4 0. 2 =0. 38 (a 1, h 2): 0. 8 0+0. 2+0. 4 0. 5+0. 6 0. 1+0. 6 0. 2 =0. 42 … C 2(a 1, h 1): 0. 8 0. 1+0. 2 0. 3+0. 4 0. 1+0. 6 0. 3+0. 4 0. 2 =0. 44 (a 1, h 2): 0. 8 0. 1+0. 2 0. 3+0. 4 0. 1+0. 6 0. 3+0. 6 0. 2 =0. 48 … Customer preferences Customer Fare Food Location Comfort Cleanness Top-2 favorites c 1 0 0 0. 2 0. 5 0. 1 0. 2 {(a 3, h 6), (a 5, h 6)} c 2 0. 1 0. 3 0. 2 {(a 3, h 2), (a 3, h 5)} c 3 0 0 0. 1 0. 3 {(a 1, h 2), (a 1, h 5)} c 4 c 5 0. 3 0 0 0. 1 0. 2 0. 3 0 0 0. 1 0. 6 {(a 1, h 5), (a 2, h 5), (a 3, h 5)} {(a 3, h 6), (a 4, h 6)} 32

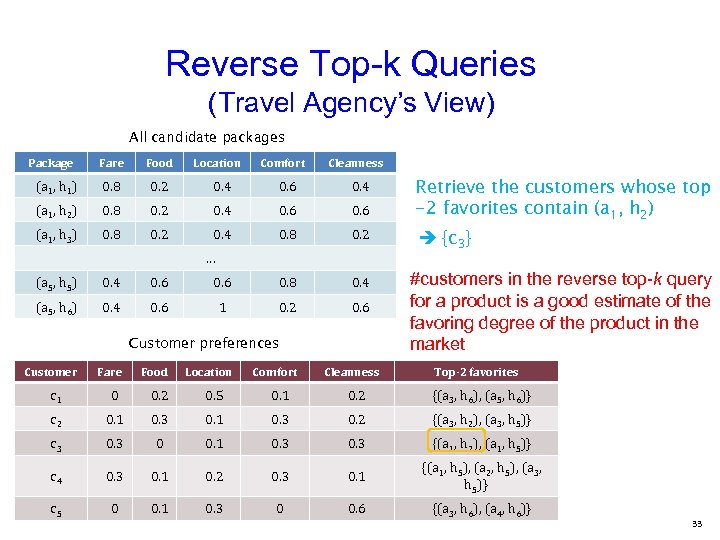Reverse Top-k Queries (Travel Agency’s View) All candidate packages Package Fare Food Location Comfort Cleanness (a 1, h 1) 0. 8 0. 2 0. 4 0. 6 0. 4 (a 1, h 2) 0. 8 0. 2 0. 4 0. 6 (a 1, h 3) 0. 8 0. 2 0. 4 0. 8 0. 2 … (a 5, h 5) 0. 4 0. 6 0. 8 0. 4 (a 5, h 6) 0. 4 0. 6 1 0. 2 0. 6 Customer preferences Customer Location Comfort Cleanness Retrieve the customers whose top -2 favorites contain (a 1, h 2) {c 3} #customers in the reverse top-k query for a product is a good estimate of the favoring degree of the product in the market Fare Food Top-2 favorites c 1 0 0. 2 0. 5 0. 1 0. 2 {(a 3, h 6), (a 5, h 6)} c 2 0. 1 0. 3 0. 2 {(a 3, h 2), (a 3, h 5)} c 3 0 0. 1 0. 3 {(a 1, h 2), (a 1, h 5)} c 4 0. 3 0. 1 0. 2 0. 3 0. 1 {(a 1, h 5), (a 2, h 5), (a 3, h 5)} c 5 0 0. 1 0. 3 0 0. 6 {(a 3, h 6), (a 4, h 6)} 33

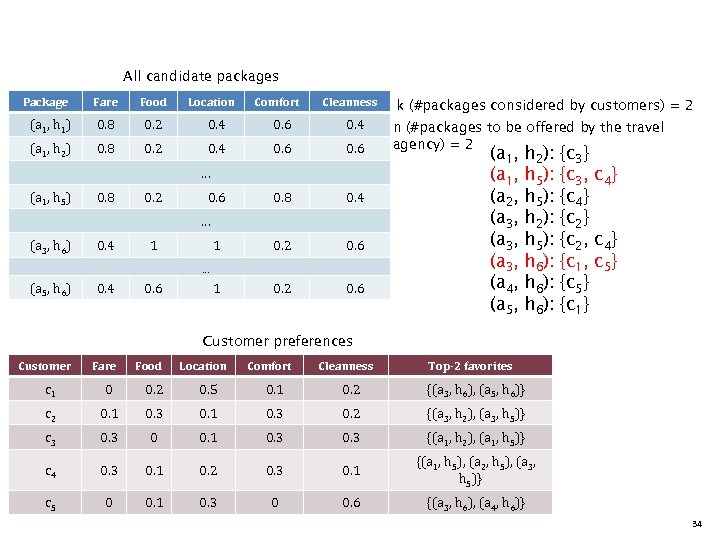All candidate packages Package Fare Food Location Comfort Cleanness (a 1, h 1) 0. 8 0. 2 0. 4 0. 6 0. 4 (a 1, h 2) 0. 8 0. 2 0. 4 0. 6 0. 8 0. 4 1 0. 2 0. 6 … (a 1, h 5) 0. 8 0. 2 0. 6 … (a 3, h 6) 0. 4 1 … (a 5, h 6) 0. 4 0. 6 k (#packages considered by customers) = 2 n (#packages to be offered by the travel agency) = 2 (a 1, (a 2, (a 3, (a 4, (a 5, h 2): h 5): h 6): {c 3} {c 3, c 4} {c 2} {c 2, c 4} {c 1, c 5} {c 1} Customer preferences Customer Fare Food Location Comfort Cleanness Top-2 favorites c 1 0 0. 2 0. 5 0. 1 0. 2 {(a 3, h 6), (a 5, h 6)} c 2 0. 1 0. 3 0. 2 {(a 3, h 2), (a 3, h 5)} c 3 0 0. 1 0. 3 {(a 1, h 2), (a 1, h 5)} c 4 0. 3 0. 1 0. 2 0. 3 0. 1 {(a 1, h 5), (a 2, h 5), (a 3, h 5)} c 5 0 0. 1 0. 3 0 0. 6 {(a 3, h 6), (a 4, h 6)} 34

Problem Definition of n-k MFP • Given a set of component tables T 1, T 2, …, and Tx, which form a set of the candidate products P, a set of customers C with different preferences on the products, and two positive integers k and n • RTOPk(cp, P, C): the set of the customers whose top-k favorites contain the candidate product cp • Retrieve the minimum subset P’ of P such that |P’| n and is maximized • Maximum coverage problem: NP-hard 35

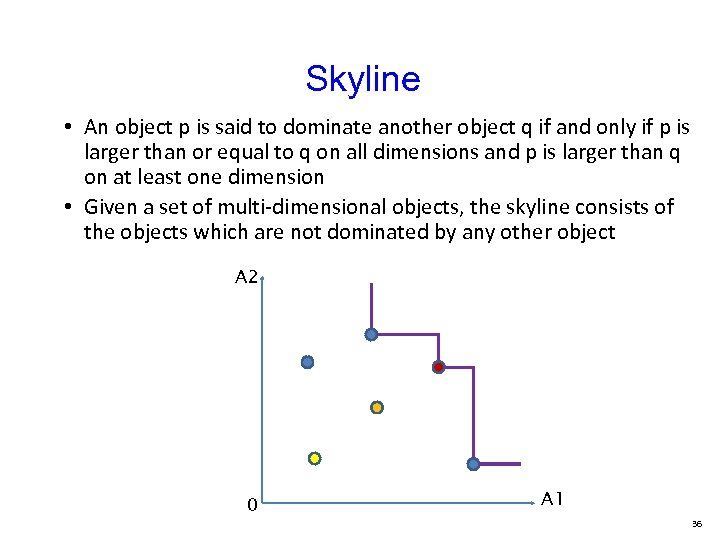Skyline • An object p is said to dominate another object q if and only if p is larger than or equal to q on all dimensions and p is larger than q on at least one dimension • Given a set of multi-dimensional objects, the skyline consists of the objects which are not dominated by any other object A 2 0 A 1 36

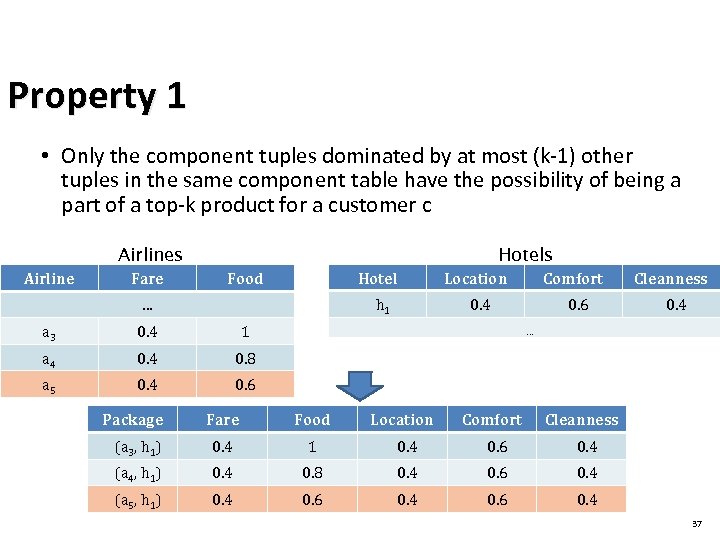Property 1 • Only the component tuples dominated by at most (k-1) other tuples in the same component table have the possibility of being a part of a top-k product for a customer c Airlines Fare Hotel Food h 1 … a 3 0. 4 Comfort 0. 4 0. 6 Cleanness 0. 4 0. 8 a 5 Location 1 a 4 Hotels 0. 6 Package … Fare Food Location Comfort Cleanness (a 3, h 1) 0. 4 1 0. 4 0. 6 0. 4 (a 4, h 1) 0. 4 0. 8 0. 4 0. 6 0. 4 (a 5, h 1) 0. 4 0. 6 0. 4 37

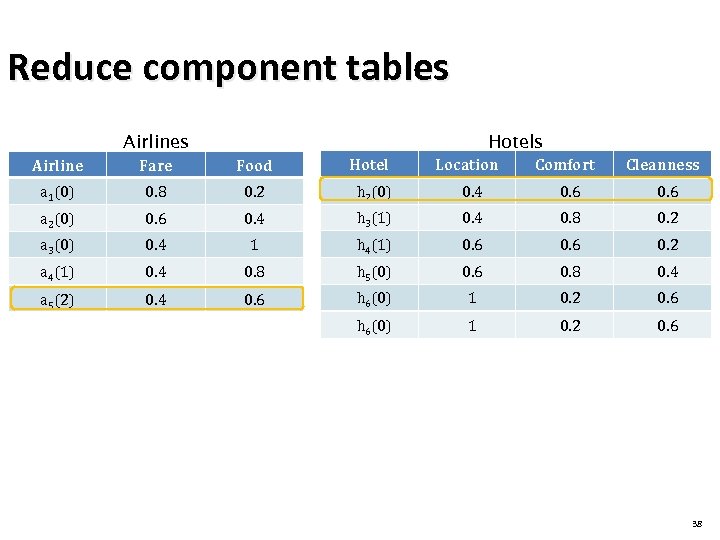Reduce component tables Airlines Hotels Location Comfort Cleanness Fare Food a 1(0) 0. 8 0. 2 h 1(2) 2(0) 0. 4 0. 6 0. 4 a 2(0) 0. 6 0. 4 h 3(1) 2(0) 0. 4 0. 8 0. 6 0. 2 0. 6 a 3(0) 0. 4 1 h 3(1) 4 0. 6 0. 8 0. 2 a 4(1) 0. 4 0. 8 h 4(1) 5(0) 0. 6 0. 8 0. 6 0. 4 0. 2 a 5(2) 0. 4 0. 6 h 6(0) 5 1 0. 6 0. 2 0. 8 0. 6 0. 4 h 6(0) 1 0. 2 0. 6 38

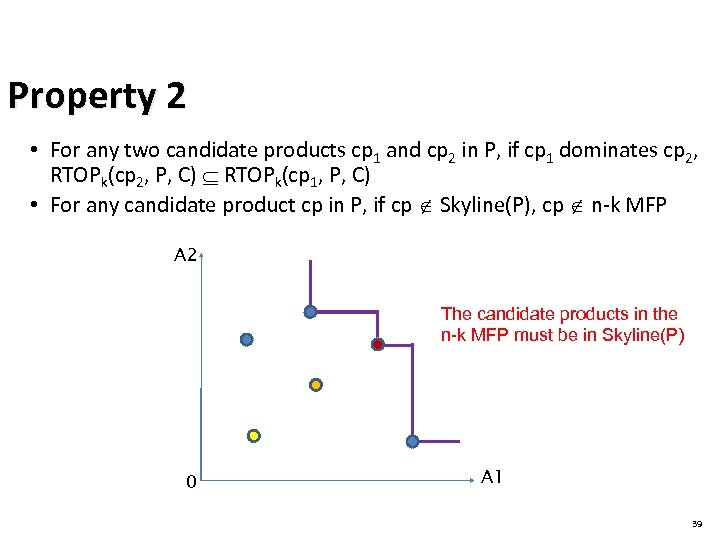Property 2 • For any two candidate products cp 1 and cp 2 in P, if cp 1 dominates cp 2, RTOPk(cp 2, P, C) RTOPk(cp 1, P, C) • For any candidate product cp in P, if cp Skyline(P), cp n-k MFP A 2 The candidate products in the n-k MFP must be in Skyline(P) 0 A 1 39

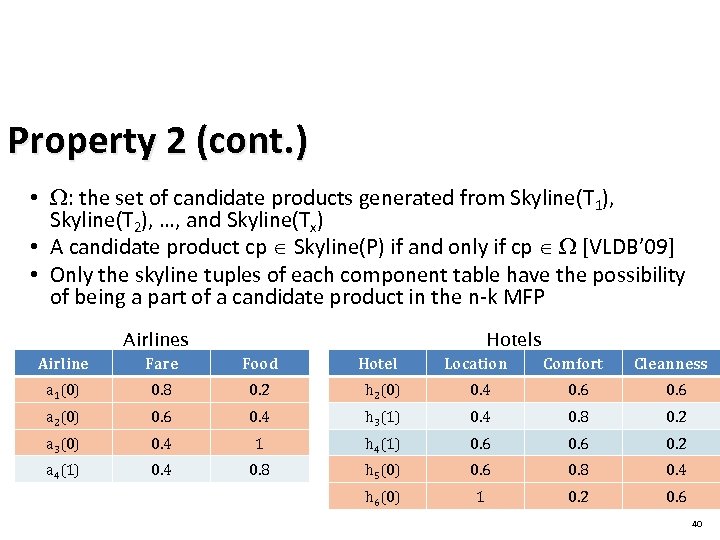Property 2 (cont. ) • : the set of candidate products generated from Skyline(T 1), Skyline(T 2), …, and Skyline(Tx) • A candidate product cp Skyline(P) if and only if cp [VLDB’ 09] • Only the skyline tuples of each component table have the possibility of being a part of a candidate product in the n-k MFP Airlines Hotels Fare Food a 1(0) 0. 8 0. 2 h 2(0) 0. 4 0. 6 a 2(0) 0. 6 0. 4 h 3(1) 0. 4 0. 8 0. 2 a 3(0) 0. 4 1 h 4(1) 0. 6 0. 2 a 4(1) 0. 4 0. 8 h 5(0) 0. 6 0. 8 0. 4 h 6(0) 1 0. 2 0. 6 Hotel Location Comfort Cleanness 40

Property 3 • Only the customers in RTOPk(cp, Skyline(P), C) possibly become the members in RTOPk(cp, P, C) The upper bounds of the remaining candidate packages Package Upper bound (a 1, h 2) {c 3} (a 1, h 5) {c 3, c 4} (a 1, h 6) {} (a 2, h 2) {} (a 2, h 5) {c 4} (a 2, h 6) {c 1, c 5} (a 3, h 2) {c 2} (a 3, h 5) {c 2, c 4} (a 3, h 6) {c 1, c 5} RTOPk(cp, Skyline(P), C) is an upper bound of RTOPk(cp, P, C) 41

Refinement Package Upper bound (a 1, h 2) {c 3} (a 1, h 5) {c 4} (a 2, h 6) {c 1, c 5} (a 3, h 2) {c 2} (a 3, h 5) {c 2, c 4} (a 3, h 6) The top-2 favorites of C 4: {(a 1, h 5), (a 2, h 5), (a 3, h 5)} {c 3, c 4} (a 2, h 5) The top-2 favorites of C 3: {(a 1, h 5), (a 1, h 2)} {c 1, c 5} P’ : {(a 1, h 5)} 42

Refinement Package Upper bound (a 2, h 6) {c 1, c 5} (a 3, h 2) {c 2} (a 3, h 6) The top-2 favorites of C 5: {(a 3, h 6), (a 4, h 6)} {c 2} (a 3, h 5) The top-2 favorites of C 1: {(a 3, h 6), (a 4, h 6)} {c 1, c 5} P’ : {(a 1, h 5), (a 3, h 6)} )} 43

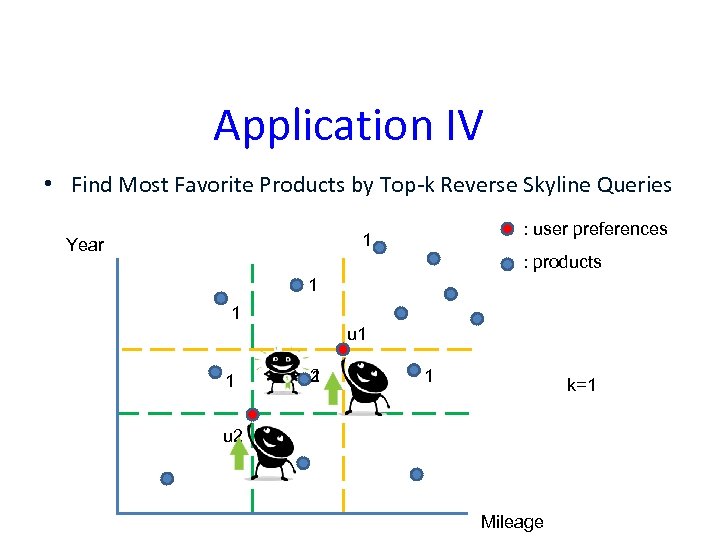Application IV • Find Most Favorite Products by Top-k Reverse Skyline Queries : user preferences 1 Year : products 1 1 u 1 1 2 1 1 k=1 u 2 Mileage

Thank you for your attention!