On the Road to Predictive Oncology Challenges for

On the Road to Predictive Oncology Challenges for Statistics and for Clinical Investigation Richard Simon, D. Sc. Chief, Biometric Research Branch National Cancer Institute http: //brb. nci. nih. gov

Biometric Research Branch Website http: //brb. nci. nih. gov • • Powerpoint presentations Reprints BRB-Array. Tools software Web based tools for clinical trial design with predictive biomarkers

Prediction Tools for Informing Treatment Selection • Most cancer treatments benefit only a minority of patients to whom they are administered • Being able to predict which patients are likely or unlikely to benefit from a treatment might – Save patients from unnecessary complications and enhance their chance of receiving a more appropriate treatment – Help control medical costs – Improve the success rate of clinical drug development

Types of Biomarkers • Predictive biomarkers – Measured before treatment to identify who is likely or unlikely to benefit from a particular treatment • Prognostic biomarkers – Measured before treatment to indicate longterm outcome for patients untreated or receiving standard treatment

• Surrogate endpoints – Measured longitudinally to measure the pace of disease and how it is effected by treatment for use as an early indication of clinical effectiveness of treatment

Prognostic & Predictive Biomarkers • Single gene or protein measurement – ER protein expression – HER 2 amplification – EGFR mutation – KRAS mutation • Index or classifier that summarizes expression levels of multiple genes – Oncotype. Dx recurrence score

Validation = Fit for Intended Use • Analytical validation – Accuracy, reproducibility, robustness • Clinical validation – Does the biomarker predict a clinical endpoint or phenotype • Clinical utility – Does use of the biomarker result in patient benefit • By informing treatment decisions • Is it actionable

Pusztai et al. The Oncologist 8: 252 -8, 2003 • 939 articles on “prognostic markers” or “prognostic factors” in breast cancer in past 20 years • ASCO guidelines only recommended routine testing for ER, PR and HER-2 in breast cancer

• Most prognostic markers or prognostic models are not used because although they correlate with a clinical endpoint, they do not facilitate therapeutic decision making; • Most prognostic marker studies are based on a “convenience sample” of heterogeneous patients, often not limited by stage or treatment. • The studies are not planned or analyzed with clear focus on an intended use of the marker • Retrospective studies of prognostic markers should be planned analyzed with specific focus on intended use of the marker • Prospective studies should address medical utility for a specific intended use of the biomarker – Treatment options and practice guidelines – Other prognostic factors

Potential Uses of Prognostic Biomarkers • Identify patients who have very good prognosis on standard treatment and do not require more intensive regimens • Identify patients who have poor prognosis on standard chemotherapy who are good candidates for experimental regimens

Predictive Biomarkers

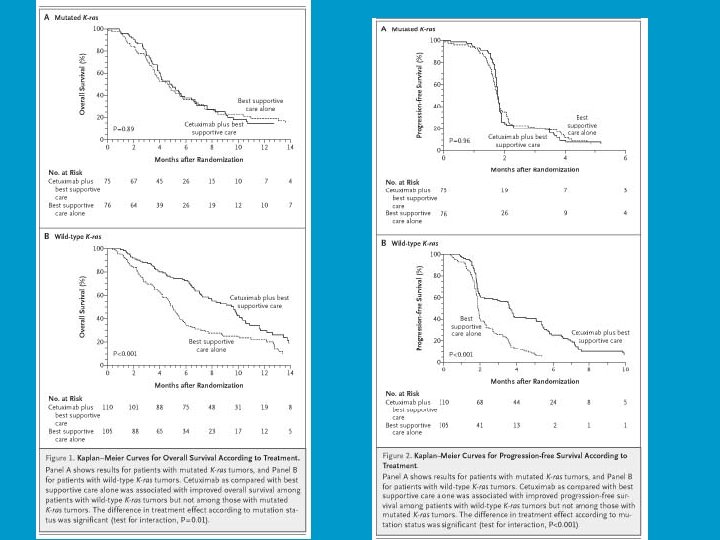
Major Changes in Oncology • Recognition of the heterogeneity of tumors of the same primary site with regard to molecular oncogenesis • Availability of the tools of genomics for characterizing tumors • Focus on molecularly targeted drugs • Have resulted in – Increased interest in prediction problems – Need for new clinical trial designs – Increased pace of innovation

• p>n prediction problems in which number of variables is much greater than the number of cases – Many of the methods of statistics are based on inference problems – Standard model building and evaluation strategies are not effective for p>n prediction problems

Model Evaluation for p>n Prediction Problems • Goodness of fit is not a proper measure of predictive accuracy • Importance of Separating Training Data from Testing Data for p>n Prediction Problems

Separating Training Data from Testing Data • Split-sample method • Re-sampling methods – Leave one out cross validation – K-fold cross validation – Replicated split-sample – Bootstrap re-sampling

• “Prediction is very difficult; especially about the future. ”

Prediction on Simulated Null Data Simon et al. J Nat Cancer Inst 95: 14, 2003 Generation of Gene Expression Profiles • 20 specimens (Pi is the expression profile for specimen i) • Log-ratio measurements on 6000 genes • Pi ~ MVN(0, I 6000) • Can we distinguish between the first 10 specimens (Class 1) and the last 10 (Class 2)? Prediction Method • Compound covariate predictor built from the log-ratios of the 10 most differentially expressed genes.

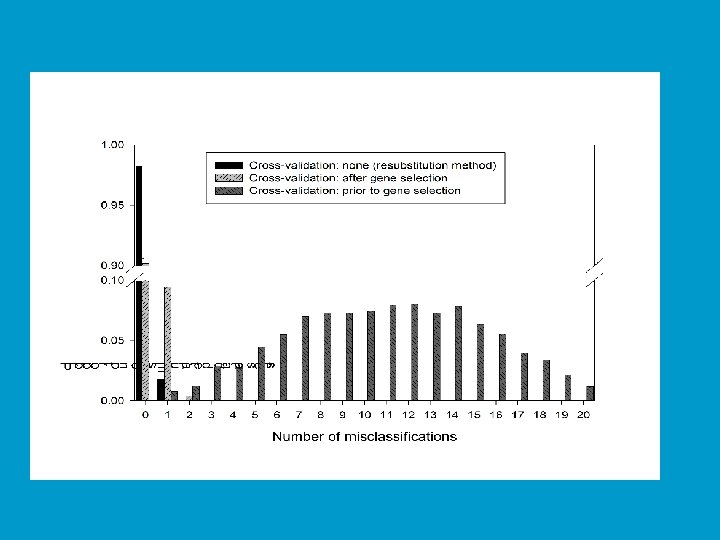
Cross Validation • With proper cross-validation, the model must be developed from scratch for each leave-one-out training set. This means that feature selection must be repeated for each leave-one-out training set. • The cross-validated estimate of misclassification error is an estimate of the prediction error for the model developed by applying the specified algorithm to the full dataset

Permutation Distribution of Cross-validated Misclassification Rate of a Multivariate Classifier Radmacher, Mc. Shane & Simon J Comp Biol 9: 505, 2002 • Randomly permute class labels and repeat the entire cross-validation • Re-do for all (or 1000) random permutations of class labels • Permutation p value is fraction of random permutations that gave as few cross-validated misclassifications as in the real data

Model Evaluation for p>n Prediction Problems • Odds ratios and hazards ratios are not proper measures of prediction accuracy • Statistical significance of regression coefficients are not proper measures of predictive accuracy

Evaluation of Prediction Accuracy • For binary outcome – Cross-validated prediction error – Cross-validated sensitivity & specificity – Cross-validated ROC curve • For survival outcome – Cross-validated Kaplan-Meier curves for predicted high and low risk groups • Cross-validated K-M curves within levels of standard prognostic staging system – Cross-validated time-dependent ROC curves

LOOCV Error Estimates for Linear Classifiers

Cross-validated Kaplan-Meier Curves for Predicted High and Low Risk Groups

Cross-Validated Time Dependent ROC Curve

Is Accurate Prediction Possible For p>n? • Yes, in many cases, but standard statistical methods for model building and evaluation are often not effective • Standard methods may over-fit the data and lead to poor predictions • With p>n, unless data is inconsistent, a linear model can always be found that classifies the training data perfectly

Is Accurate Prediction Possible For p>>n? • Some problems are easy; real problems are often difficult • Simple methods like DLDA, nearest neighbor classifiers and shrunken centroid classifiers are at least as effective as more complex methods for many datasets • Because of correlated variables, there are often many very distinct models that predict about equally well

• p>n prediction problems are not multiple testing problems • The objective of prediction problems is accurate prediction, not controlling the false discovery rate – Parameters that control feature selection in prediction problems are tuning parameters to be optimized for prediction accuracy • Optimizaton by cross-validation nested within the crossvalidation used for evaluating prediction accuracy • Biological understanding is often a career objective; accurate prediction can sometimes be achieved in less time

Model Instability Does Not Mean Prediction Inaccuracy • Validation of a predictive model means that the model predicts accurately for independent data • Validation does not mean that the model is stable or that using the same algorithm on independent data will give a similar model • With p>n and many genes with correlated expression, the classifier will not be stable.

Traditional Approach to Oncology Clinical Drug Development • Phase III trials with broad eligibility to test the null hypothesis that a regimen containing the new drug is on average not better than the control treatment for all patients who might be treated by the new regimen • Perform exploratory subset analyses but regard results as hypotheses to be tested on independent data

Traditional Clinical Trial Approaches • Have protected us from false claims resulting from post-hoc data dredging not based on predefined biologically based hypotheses • Have led to widespread over-treatment of patients with drugs from which many don’t benefit • Are less suitable for evaluation of new molecularly targeted drugs which are expected to benefit only the patients whose tumors are driven by de-regulation of the target of the drug

Molecular Heterogeneity of Human Cancer • Cancers of a primary site in many cases appear to represent a heterogeneous group of diverse molecular diseases which vary fundamentally with regard to – their oncogenecis and pathogenesis – their responsiveness to specific drugs • The established molecular heterogeneity of human cancer requires the use new approaches to the development and evaluation of therapeutics

How Can We Develop New Drugs in a Manner More Consistent With Modern Tumor Biology and Obtain Reliable Information About What Regimens Work for What Kinds of Patients?

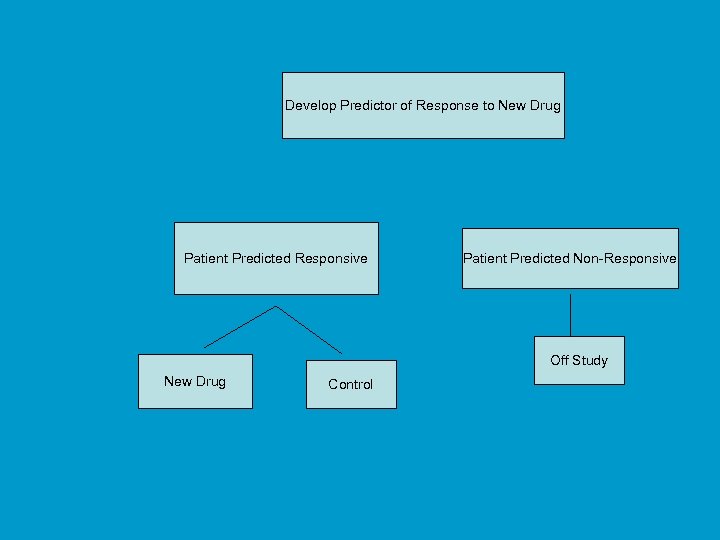Using phase II data, develop predictor of response to new drug Develop Predictor of Response to New Drug Patient Predicted Responsive Patient Predicted Non-Responsive Off Study New Drug Control

Evaluating the Efficiency of Enrichment and Stratification Clinical Trial Designs With Predictive Biomarkers • • Simon R and Maitnournam A. Evaluating the efficiency of targeted designs for randomized clinical trials. Clinical Cancer Research 10: 6759 -63, 2004; Correction and supplement 12: 3229, 2006 Maitnournam A and Simon R. On the efficiency of targeted clinical trials. Statistics in Medicine 24: 329 -339, 2005.

Model for Two Treatments With Binary Response • New treatment T • Control treatment C • 1 - proportion marker + • pc control response probability • response probability for T: –Marker + (pc + 1) –Marker - (pc + 0)

Randomized Ratio (normal approximation) • Rand. Rat = nuntargeted/ntargeted • • • 1= rx effect in marker + patients 0= rx effect in marker - patients =proportion of marker - patients If 0=0, Rand. Rat = 1/ (1 - ) 2 If 0= 1/2, Rand. Rat = 1/(1 - /2)2

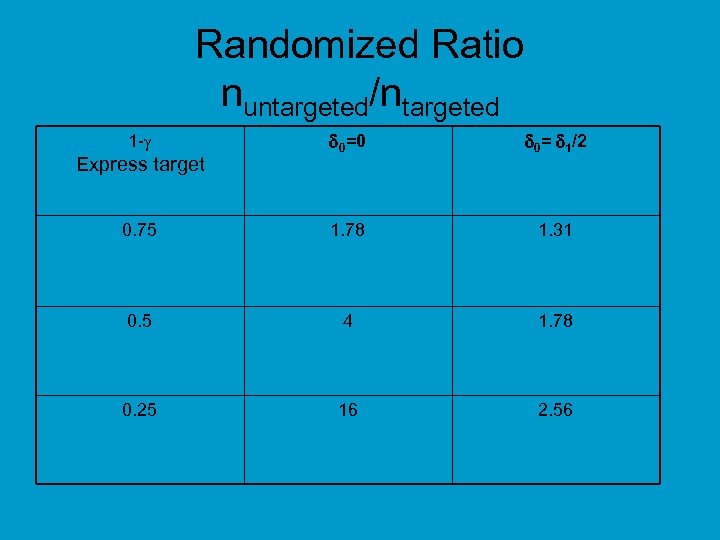Randomized Ratio nuntargeted/ntargeted 0=0 0= 1/2 0. 75 1. 78 1. 31 0. 5 4 1. 78 0. 25 16 2. 56 1 - Express target

• Relative efficiency of targeted design depends on – proportion of patients test positive – effectiveness of new drug (compared to control) for test negative patients • When less than half of patients are test positive and the drug has little or no benefit for test negative patients, the targeted design requires dramatically fewer randomized patients

Trastuzumab Herceptin • Metastatic breast cancer • 234 randomized patients per arm • 90% power for 13. 5% improvement in 1 -year survival over 67% baseline at 2 -sided. 05 level • If benefit were limited to the 25% assay + patients, overall improvement in survival would have been 3. 375% – 4025 patients/arm would have been required

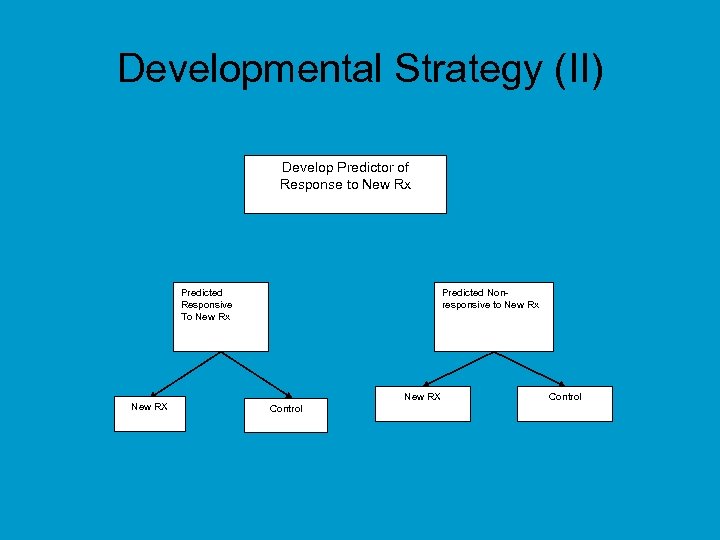Developmental Strategy (II) Develop Predictor of Response to New Rx Predicted Responsive To New Rx New RX Predicted Nonresponsive to New Rx New RX Control

Developmental Strategy (II) • Do not use the diagnostic to restrict eligibility, but to structure a prospective analysis plan • Having a prospective analysis plan is essential • “Stratifying” (balancing) the randomization is useful to ensure that all randomized patients have tissue available but is not a substitute for a prospective analysis plan • The purpose of the study is to evaluate the new treatment overall and for the pre-defined subsets; not to modify or refine the classifier

• R Simon. Using genomics in clinical trial design, Clinical Cancer Research 14: 5984 -93, 2008 • R Simon. Designs and adaptive analysis plans for pivotal clinical trials of therapeutics and companion diagnostics, Expert Opinion in Medical Diagnostics 2: 721 -29, 2008

Analysis Plan B (Fall-back Plan) • Compare the new drug to the control overall for all patients ignoring the classifier. – If poverall 0. 03 claim effectiveness for the eligible population as a whole • Otherwise perform a single subset analysis evaluating the new drug in the classifier + patients – If psubset 0. 02 claim effectiveness for the classifier + patients.

Analysis Plan C (Interaction Plan) • Test for difference (interaction) between treatment effect in test positive patients and treatment effect in test negative patients • If interaction is significant at level int then compare treatments separately for test positive patients and test negative patients • Otherwise, compare treatments overall

Sample Size Planning for Analysis Plan C • 88 events in test + patients needed to detect 50% reduction in hazard at 5% twosided significance level with 90% power • If 25% of patients are positive, when there are 88 events in positive patients there will be about 264 events in negative patients – 264 events provides 90% power for detecting 33% reduction in hazard at 5% two-sided significance level

Simulation Results for Analysis Plan C • Using int=0. 10, the interaction test has power 93. 7% when there is a 50% reduction in hazard in test positive patients and no treatment effect in test negative patients • A significant interaction and significant treatment effect in test positive patients is obtained in 88% of cases under the above conditions • If the treatment reduces hazard by 33% uniformly, the interaction test is negative and the overall test is significant in 87% of cases

• It can be difficult to identify a single completely defined classifier candidate prior to initiation of the phase III trial evaluating the new treatment

Generalization of Biomarker Adaptive Threshold Design (Global Test Approach) • Have identified K candidate predictive binary classifiers B 1 , …, BK thought to be predictive of patients likely to benefit from T relative to C • Eligibility not restricted by candidate biomarkers

End of Trial Analysis • Compare T to C for all patients at significance level overall (e. g. 0. 03) – If overall H 0 is rejected, then claim effectiveness of T for eligible patients – Otherwise

• Test T vs C restricted to patients positive for Bk for k=1, …, K – Let Sk be log likelihood ratio statistic for treatment effect in patients positive for Bk (k=1, …, K) • Let S* = max{Sk)} , k* = argmax{Sk)} • Compute null distribution of S* by permuting treatment labels • If the unpermutted data value of S* is significant at level 0. 05 - overall , claim effectiveness of T for patients positive for Bk*

Cross-Validated Adaptive Signature Design (Clinical Cancer Research, Jan 2010) W Jiang, B Freidlin, R Simon

Cross-Validated Adaptive Signature Design End of Trial Analysis • Compare T to C for all patients at significance level overall (e. g. 0. 03) – If overall H 0 is rejected, then claim effectiveness of T for eligible patients – Otherwise

Otherwise • Partition the full data set into K parts P 1 , …, PK • Form a training set by omitting one of the K parts, e. g. part k. – Trk={1, …, n}-Pk • The omitted part Pk is the test set • Using the training set, develop a predictive binary classifier B-k of the subset of patients who benefit preferentially from the new treatment compared to control • Classify the patients i in the test set as sensitive B-k(xi)=1 or insensitive B-k(xi)=0 – Let Sk={j in Pk : B-k(xi)=1}

• Repeat this procedure K times, leaving out a different part each time • After this is completed, all patients in the full dataset are classified as sensitive or insensitive – Scv= Sk

• For patients classified as sensitive, compare outcomes for patients who received new treatment T to those who received control treatment C. – Outcomes for patients in Scv T vs outcomes for patients in Scv C • Compute a test statistic Dsens – e. g. the difference in response proportions or log-rank statistic for survival • Generate the null distribution of Dsens by permuting the treatment labels and repeating the entire K-fold cross-validation procedure • Perform test at significance level 0. 05 - overall

• If H 0 is rejected, claim superiority of new treatment T for future patients with expression vector x for which B(x)=1 where B is the classifier of sensitive patients developed using the full dataset • The estimate of treatment effect for future sensitive patients is Dsens computed from the cross-validated sensitive subset Scv • The stability of the sensitive subset {x: B(x)=1} can be evaluated based on applying the classifier development algorithm to non-parametric bootstrap samples of the full dataset {1, . . . , n}

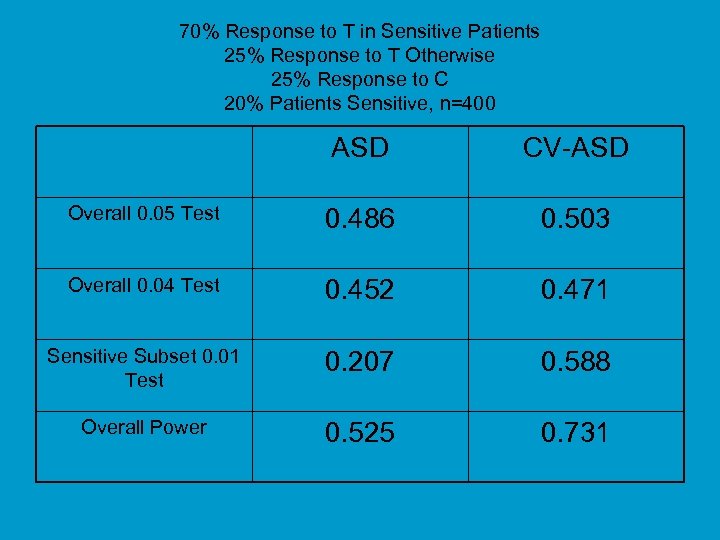70% Response to T in Sensitive Patients 25% Response to T Otherwise 25% Response to C 20% Patients Sensitive, n=400 ASD CV-ASD Overall 0. 05 Test 0. 486 0. 503 Overall 0. 04 Test 0. 452 0. 471 Sensitive Subset 0. 01 Test 0. 207 0. 588 Overall Power 0. 525 0. 731

Prediction Based Analysis of Clinical Trials • Using cross-validation we can evaluate any classification algorithm for identifying the patients sensitive to the new treatment relative to the control using any set of covariates. • The algorithm and covariates should be pre-specified. • The algorithm A, when applied to a dataset D should provide a function B(x; A, D) that maps a covariate vector x to {0, 1}, where 1 means that treatment T is prefered to treatment C for the patient. • The algorithm can be simple or complex, frequentist or Bayesian based. – Prediction effectiveness depends on the algorithm and the dataset – Complex algorithms may over-fit the data and provide poor results • Including Bayesian models with many parameters and non-informative priors • Prediction effectiveness for the given clinical trial dataset can be evaluated by cross-validation

Conclusions • A more personalized oncology is rapidly developing based (so far) on information in the tumor genome • Genomics has spawned new and interesting areas of biostatistics including methods for p>n prediction problems, systems biology and the design of predictive clinical trials • There are important opportunities and great needs for young biostatisticians with rigorous training in biostatistics and high motivation for trans-disciplinary research in biology and biomedicine

Acknowledgements • • Kevin Dobbin Boris Freidlin Wenyu Jiang Aboubakar Maitournam Michael Radmacher Jyothi Subramarian Yingdong Zhao

BRB-Array. Tools • Architect – R Simon • Developer – Emmes Corporation • Contains wide range of analysis tools that I have selected • Designed for use by biomedical scientists • Imports data from all gene expression and copy-number platforms – Automated import of data from NCBI Gene Express Omnibus • Highly computationally efficient • Extensive annotations for identified genes • Integrated analysis of expression data, copy number data, pathway data and data other biological data

Predictive Classifiers in BRB-Array. Tools • Classifiers • – – – Univariate t/F statistic – Hierarchical random variance model – Restricted by fold effect – Univariate classification power – Recursive feature elimination – Top-scoring pairs Diagonal linear discriminant Compound covariate Bayesian compound covariate Support vector machine with inner product kernel – K-nearest neighbor – Nearest centroid – Shrunken centroid (PAM) – Random forrest – Tree of binary classifiers for kclasses • • • Predict quantitative trait – LARS, LASSO Validation methods – – Survival risk-group – Supervised pc’s – With clinical covariates – Cross-validated K-M curves Feature selection options • Split-sample LOOCV Repeated k-fold CV. 632+ bootstrap Permutational statistical significance

BRB-Array. Tools June 2009 • 10, 000+ Registered users • 68 Countries • 1000+ Citations