On the Performance of Linear Slepian-Wolf Codes Shengtian

On the Performance of Linear Slepian-Wolf Codes Shengtian Yang and Peiliang Qiu Dept. of Inform. Sci. /Electron. Eng. Zhejiang University Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian. Wolf Codes 1

Overview n n The history of the Slepian-Wolf theorem Our work on the performance of (linear) Slepian-Wolf codes n n n The method for upper-bounding the MAP decoding error of Slepian-Wolf codes The performance of linear Slepian-Wolf codes (e. g. , SW codes based on LPDC codes) A symmetric coding scheme Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 2

Three milestones n Statistically dependent Encoder D. Slepian and J. K. Wolf, 1973[1] for stationary memoryless sources Decoder Encoder Mar. 29, 2005 Slepian-Wolf Theorem S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 3

n n n T. M. Cover, 1975[2] for stationary and ergodic sources S. Miyake and F. Kanaya, 1995[3] for general sources The ensemble of codes in their proofs are purely random. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 4

Performance of linear codes n n I. Csiszar, 1982[4] There exist good universal linear codes for correlated memoryless sources. T. Uyematsu, 2001[5] There exist good universal codes for correlated sources with memory, and such codes can be constructed by algebraic geometric codes. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 5

n J. Muramatsu, T. Uyematsu, and T. Wadayama, 2003[6] There exist good binary LDPC codes for correlated general sources. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 6

Our work on the Performance of Slepian-Wolf Codes n n Inspired in part by Gallager’s method. The Gallager bound is well known in the area of channel coding. n n R. G. Gallager, 1965[7], A basic upper bound for random code ensembles, DMCs and ML decoding A. Bennatan and D. Burshtein, 2004[8], An improved upper bound for linear random code ensembles, DMCs and ML decoding Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 7

The Gallager bound n Typical form of the basic Gallager bound Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 8

Gallager’s Method n Two basic inequalities The common union bound in Gallager’s book [9] is an easy derivation of the second inequality. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 9

The upper bounds on the MAP decoding error of SW codes n n A basic upper bound for correlated general sources (i. e. Theorem 1) (For single source coding, a similar upper bound has been obtained by Gallager in his book [9, Exercise 5. 16]. ) An improved upper bound of linear SW codes for correlated SMSs (i. e. Theorem 3) Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 10

The basic upper bound of SW codes for general sources Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 11

Two typical forms of the error exponents n 1) typical form for analytic properties n 2) typical form for asymptotic properties Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 12

First order derivative of J 0(x) Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 13

Second order derivative of J 0 ( x) Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 14

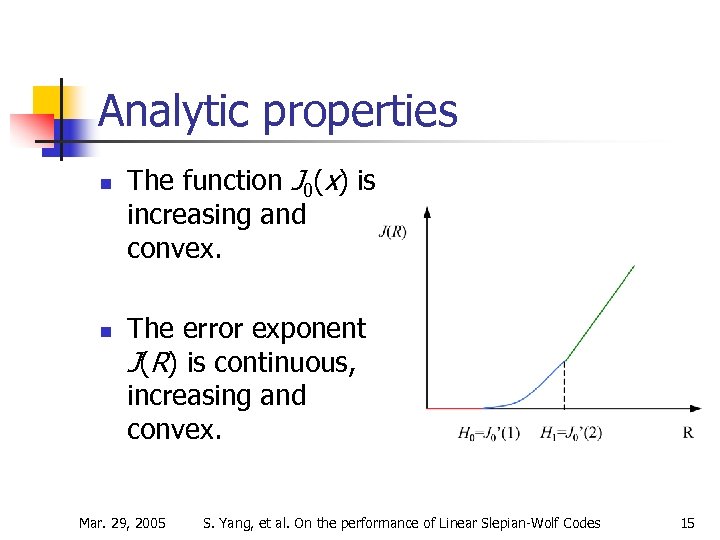Analytic properties n n The function J 0(x) is increasing and convex. The error exponent J(R) is continuous, increasing and convex. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 15

Asymptotic properties n By this result (i. e. Theorem 2), we can prove the direct part of Slepian-Wolf theorem for general sources. Analogously, we showed in [10] that the Gallager bound is also very tight even for general channels. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 16

The improved upper bound of linear SW codes for SMSs Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 17

The spectrum n n The performance of linear SW codes are mainly determined by the code’s spectrum. A code approaching random spectrum is good. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 18

The performance of codes based on regular LDPC codes Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 19

The performance of codes based on permutations Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 20

Implications of Theorem 4, 5 n n Theorem 4: If the parameters d (of LDPC codes) and n (the length of codes) are large enough, all but a diminishingly small proportion of the regular LDPC encoders can achieve asymptotically vanishing probability of MAP decoding error for any rate pair in the achievable rate region of the correlated SMSs. Theorem 5: if n is sufficiently large, most permutations are good enough to help us build perfect SW systems based on a small number of good encoders. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 21

How to design a symmetric SW coding scheme n Current methods in practice n Encoding n n n Channel code partitioning Source splitting Decoding n Mar. 29, 2005 Iterative decoding using the joint distribution S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 22

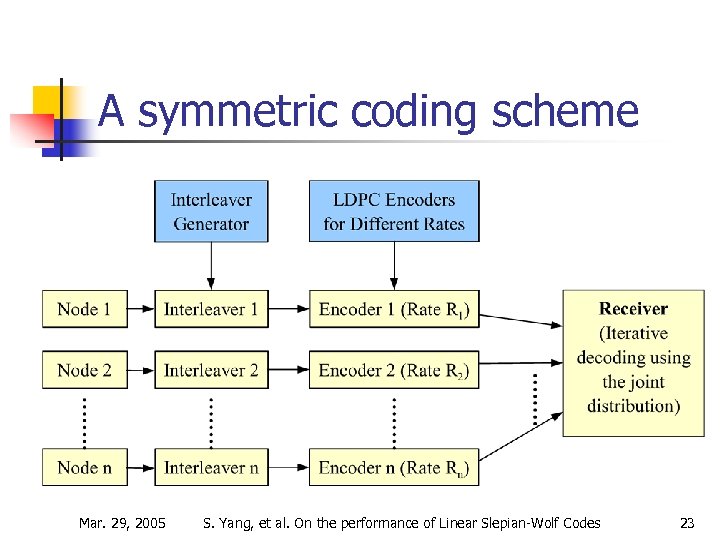A symmetric coding scheme Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 23

Future work n n Performance analysis of iterative decoding Interleaver design Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 24

Thank you! An appendix including all the omitted proofs in our paper is available at my personal web site http: //datacompression. zj. com Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian. Wolf Codes 25

Reference [1] D. Slepian and J. K. Wolf, “Noiseless coding of correlated information sources, ” IEEE Trans. Inform. Theory, vol. 19, no. 4, pp. 471 -480, July 1973. [2] T. M. Cover, “A proof of the data compression theorem of Slepian and Wolf for ergodic sources, ” IEEE Trans. Inform. Theory, vol. 21, no. 2, pp. 226 -228, Mar. 1975. [3] S. Miyake and F. Kanaya, “Coding theorems on correlated general sources, ” IEICE Trans. Fundamentals, vol. E 78 -A, no. 9, pp. 1063 -1070, Sept. 1995. [4] I. Csiszar, “Linear codes for sources and source networks: Error exponents, universal coding, ” IEEE Trans. Inform. Theory, vol. 28, no. 4, pp. 585 -592, July 1982. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 26

[5] T. Uyematsu, “Universal coding for correlated sources with memory, ” in Proc. CWIT 2001, Vancouver, BC, Canada, June 2001. [6] J. Muramatsu, T. Uyematsu, and T. Wadayama, “Low density parity check matrices for coding of correlated sources, ” in Proc. ISIT 2003, Yokohama, Japan, June 2003, p. 173. [7] R. G. Gallager, “A simple derivation of the coding theorem and some applications, ” IEEE Trans. Inform. Theory, vol. 11, no. 1, pp. 3 -8, Jan. 1965. [8] A. Bennatan and D. Burshtein, “On the application of LDPC codes to arbitrary discrete-memoryless channels, ” IEEE Trans. Inform. Theory, vol. 50, no. 3, pp. 417 -437, Mar. 2004. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 27

[9] R. G. Gallager, Information Theory and Reliable Communication. New York: Wiley, 1968. [10] S. Yang and P. Qiu, “Some extensions of Gallager’s method to general sources and channels, ” submitted to ISIT 2005. Mar. 29, 2005 S. Yang, et al. On the performance of Linear Slepian-Wolf Codes 28