19d9fbda0b6a9e21e3cd5a9bd30a19b8.ppt
- Количество слайдов: 68

On the (in)security of the random number generators of Linux and Windows Benny Pinkas, University of Haifa Zvi Gutterman, Leo Dorrendorf, Tzachy Reinman, Hebrew University

In this talk p What are PRNGs (pseudo-random number generators)? n p The generator used by Windows n p Its algorithm, and its weaknesses. A little on the generator used by Linux n p Why are they important? Why should the generators of Windows/Linux be investigated? Its algorithm, and its weaknesses. Security issues when using a generator in a systems without a hard disk.

Why are random number generators important?

Usage of random bits Many applications need random bits for their operation p This is particularly true for security applications p p All cryptosystems are only secure if they use random keys n “… Pick a key K at random …” In practice looks like Crypt. Gen. Random(Key, 16) n Relevant for SSL, SSH, etc. n

Usage of random bits: session ids p http is stateless. Session ids can make http stateful. Session id, blah-blah n Knowledge of session ids enables to impersonate clients. n n Session ids must therefore be random/unpredictable. [GM 05] showed how to guess session ids in the Apache Java implementation for Servlet 2. 4

Usage of random bits: preventing TCP spoofing TCP sequence numbers should be unpredictable p to prevent “packet spoofing” p n n p I. e. , prevent attackers from pretending to come from fake IP addresses "completing" a TCP handshake with a victim server without ever receiving any responses from the server. Predictable TCP sequence numbers enable such attacks

Security of random number generators

Security Applications are designed to be secure when using truly random bits p Random bits are hard to get p n n n instead use pseudo-random bits (from a pseudorandom number generator - PRNG) Applications are now only secure if pseudo-random bits are indistinguishable from random Otherwise an attacker can, e. g. , Guess cryptographic keys (SSL in Netscape [GW 96]) p Guess session ids (Apache session ids [GM 05]) p
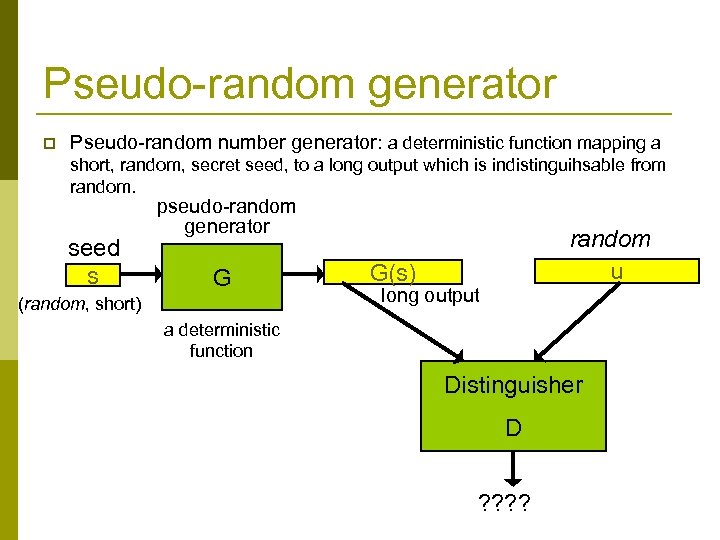
Pseudo-random generator p Pseudo-random number generator: a deterministic function mapping a short, random, secret seed, to a long output which is indistinguihsable from random. seed s pseudo-random generator G (random, short) random u G(s) long output a deterministic function Distinguisher D ? ?

Possible Random Number Generators p Pure hardware generator (of true randomness) n p Application based PRNGs n n n p Cost / portability / interface issues Too little noise available for seeding Implementer can make mistakes (The generators provided by most programming languages are insecure for security related applications) Operating system based PRNGs n n n Seeding can use system based noise/entropy (process scheduling, hard disk timing, etc. ) PRNG can be implemented and hidden in the kernel Implementer is less likely to make mistakes…

Why investigate the PRNGs of major operating systems? p Implementers of applications use the pseudorandom number generators provided by the major operating systems n n But… The algorithms and code of these generators were never published ! We don’t know how they are initialized ! Yet their output is crucial for almost any security application !
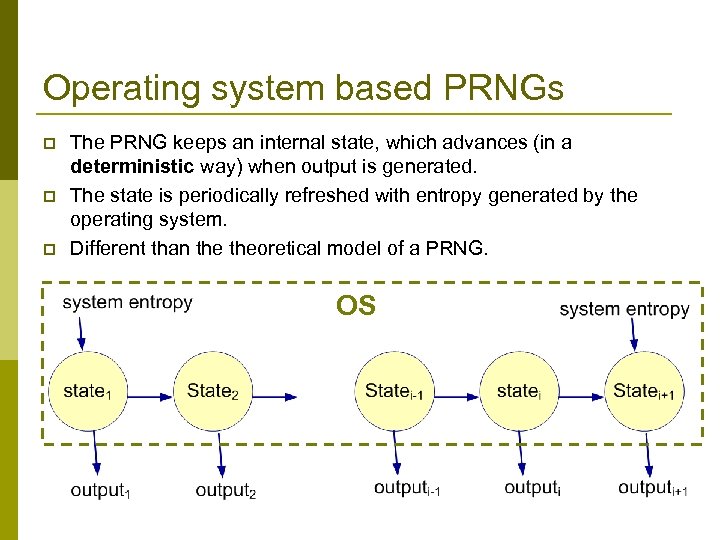
Operating system based PRNGs p p p The PRNG keeps an internal state, which advances (in a deterministic way) when output is generated. The state is periodically refreshed with entropy generated by the operating system. Different than theoretical model of a PRNG. OS
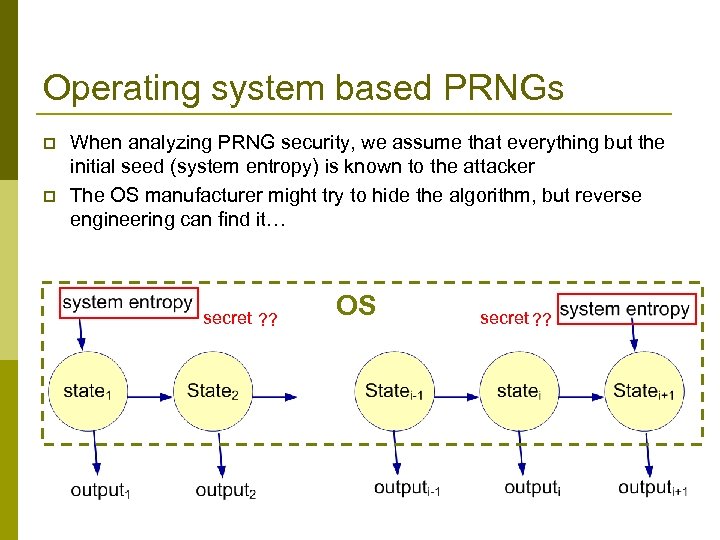
Operating system based PRNGs p p When analyzing PRNG security, we assume that everything but the initial seed (system entropy) is known to the attacker The OS manufacturer might try to hide the algorithm, but reverse engineering can find it… secret ? ? OS secret ? ?

Desired security properties
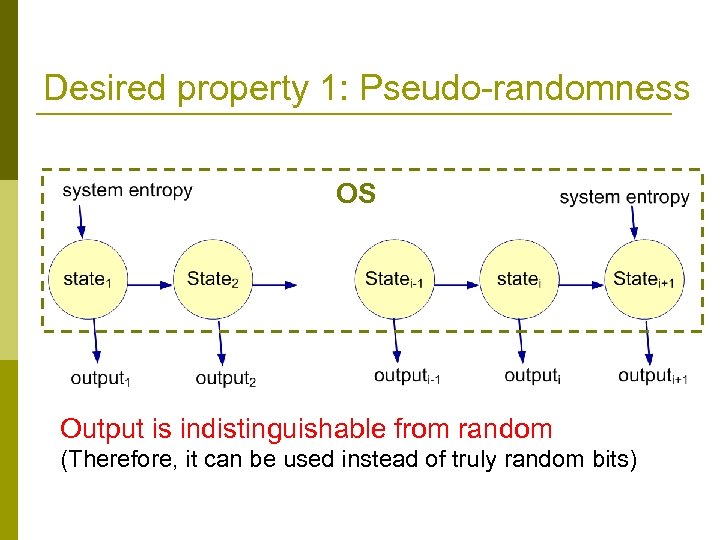
Desired property 1: Pseudo-randomness OS Output is indistinguishable from random (Therefore, it can be used instead of truly random bits)
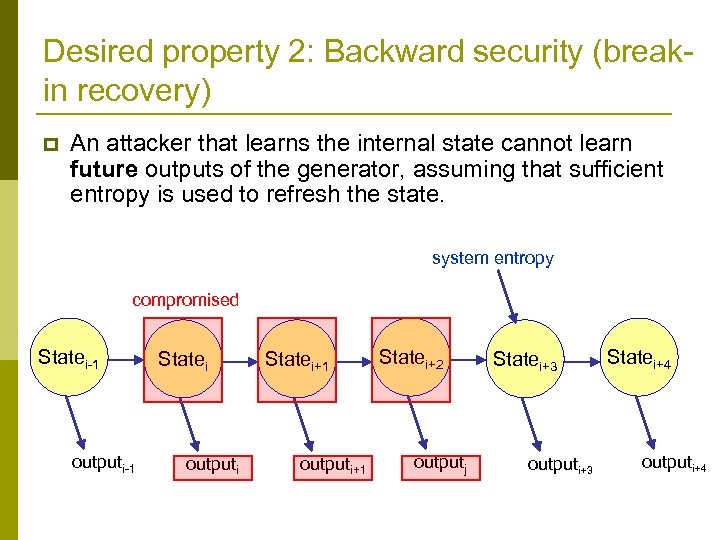
Desired property 2: Backward security (breakin recovery) p An attacker that learns the internal state cannot learn future outputs of the generator, assuming that sufficient entropy is used to refresh the state. system entropy compromised Statei-1 outputi-1 Statei outputi Statei+1 outputi+1 Statei+2 outputj Statei+3 outputi+3 Statei+4 outputi+4
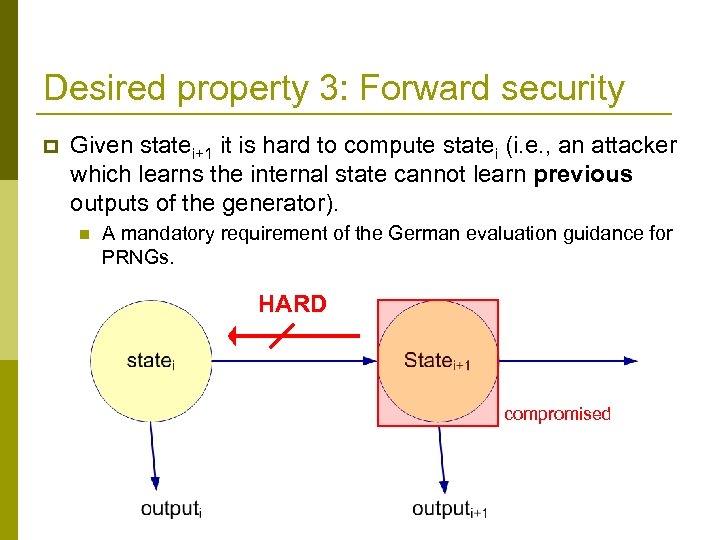
Desired property 3: Forward security p Given statei+1 it is hard to compute statei (i. e. , an attacker which learns the internal state cannot learn previous outputs of the generator). n A mandatory requirement of the German evaluation guidance for PRNGs. HARD compromised

Why is forward security important? p Security systems are secure as long as attackers cannot access secret keys n p Determined attackers might be able to access keys How can we minimize the damage of key exposure?

Minimizing the damage of key exposure p Threshold crypto: (space dimension) n n p Proactive crypto (space + time) n p Use n servers. Critical operations require participation of t (<n) servers. Attacker must break into t servers in order to break security. Example: secret sharing, threshold signatures. At end of every day the n servers exchange messages and change their state. Attacker must break into t servers at the same day to break security. Disadvantages: At least t servers are needed for any operation (e. g. , signatures).

Key evolution Use time dimension. p The sensitive information (e. g. key) is frequently updated. p Adversary which learns the current key cannot break security of past operations. p p “Forward security”: current users do not have to worry about attacks which might happen in the future.
![Forward secure PRGs [K, BY, BH] p Also, the proof of the HILL construction Forward secure PRGs [K, BY, BH] p Also, the proof of the HILL construction](https://present5.com/presentation/19d9fbda0b6a9e21e3cd5a9bd30a19b8/image-21.jpg)
Forward secure PRGs [K, BY, BH] p Also, the proof of the HILL construction of PRGs from one-way functions can be extended to show forward security.

Forward secure signatures A single public verification key. p A different private signature key per day. p n Signatures with all private keys can be verified with the same public key. p At the end of the day the signature key is erased. p Forward security: An attacker which obtains today’s private signature key, cannot learn the keys of previous days.
![Forward secure signatures p Basic scheme [Anderson] n n n Private keys: a certification Forward secure signatures p Basic scheme [Anderson] n n n Private keys: a certification](https://present5.com/presentation/19d9fbda0b6a9e21e3cd5a9bd30a19b8/image-23.jpg)
Forward secure signatures p Basic scheme [Anderson] n n n Private keys: a certification key + 365 day keys Public key: public verification key of certification key Initialization: p p n Day i: p p Sign using Ki. Add to the signature the verification key PKi, and the certificate of day i. Erase Ki at end of day. Improvement [K]: n p Use certification key to sign 365 certificates: “Key PKi is the public verification key of day i”. Erase certification key O(1) storage. Use a forward-secure PRG to generate private day keys. Sign certificates using a hash tree. Many more improvements (time vs. space).

Cryptanalysis of the Windows random number generator With Leo Dorrendorf, Zvi Gutterman Hebrew University ACM CCS 2007

Crypt. Gen. Random The only API provided by Windows OS for getting secure random numbers p The world’s most common PRNG p Used by Internet Explorer to generate SSL keys p p Its exact design and code were unknown (until now) n Security by obscurity?

Our research p Examined the binary code of Windows 2000 n n p Identified the algorithm used by the PRNG n n n p Windows 2000 is still the 2 nd/3 rd most popular OS PRNGs of all Windows systems are said to be similar Did not have access to the source code. Used static and dynamic reverse engineering. This was not easy. Verified the algorithm by writing a user-mode simulator which outputs the same values as the OS. Showed attacks on forward and backward security

The main loop (never before published!) Crypt. Gen. Random (Buffer , Len) // output Len bytes to buffer while (Len >0) { R : = R get_next_20_rc 4_bytes () State : = State R T : = SHA-1’( State ) Buffer : = Buffer | T // | denotes concatenation R[0. . 4] : = T[0. . 4] // copy 5 least significant bytes State : = State + R + 1 Len : = Len − 20 }

Two 20 byte long registers Crypt. Gen. Random (Buffer , Len) // output Len bytes to buffer while (Len >0) { R : = R get_next_20_rc 4_bytes () State : = State R SHA-1 is a hash function T : = SHA-1’( State ) output Buffer : = Buffer | T // | denotes concatenation R[0. . 4] : = T[0. . 4] // copy 5 least significant bytes State : = State + R + 1 Len : = Len − 20 }

Uses RC 4 and SHA 1 Several instances of Crypt. Gen. Random (Buffer , Len) RC 4 generate output // output Len bytes to buffer used by the generator while (Len >0) { R : = R get_next_20_rc 4_bytes () State : = State R RC 4 is a stream cipher T : = SHA-1’( State ) Buffer : = Buffer | T // | denotes concatenation R[0. . 4] : = T[0. . 4] // copy 5 least significant bytes State : = State + R + 1 Len : = Len − 20 }

Odd usage of and + Crypt. Gen. Random (Buffer , Len) // output Len bytes to buffer while (Len >0) { R : = R get_next_20_rc 4_bytes () State : = State R T : = SHA-1’( State ) Buffer : = Buffer | T // | denotes concatenation R[0. . 4] : = T[0. . 4] // copy 5 least significant bytes State : = State + R + 1 Len : = Len − 20 }

Crypt. Gen. Random p Scoping: a different state is kept for every thread RC 4 states in static DLL space. R and State stored in the stack. p For an attacker, it is easier to learn this data compared to a system where this data is stored in the kernel. p p Initialization gathers 3584 bytes of system data (most of this data is predictable). n n n p Internal states, OS and CPU queries, registry keys, etc. Applies SHA 1 and RC 4 to this data to compute the initial RC 4 states. Initialization is crucial for security. Reseeding: after a process reads 128 Kbytes of output from Crypt. Gen. Random initialization is repeated. n New system entropy is only collected at time of rekeying.
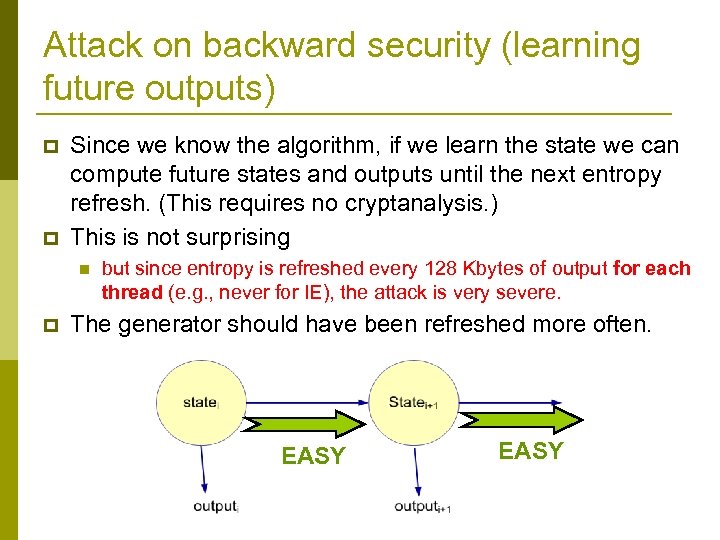
Attack on backward security (learning future outputs) p p Since we know the algorithm, if we learn the state we can compute future states and outputs until the next entropy refresh. (This requires no cryptanalysis. ) This is not surprising n p but since entropy is refreshed every 128 Kbytes of output for each thread (e. g. , never for IE), the attack is very severe. The generator should have been refreshed more often. EASY
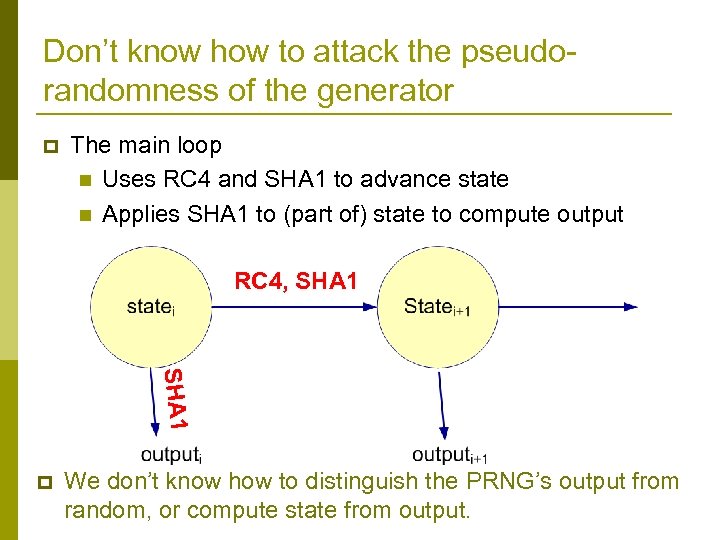
Don’t know how to attack the pseudorandomness of the generator p The main loop n Uses RC 4 and SHA 1 to advance state n Applies SHA 1 to (part of) state to compute output RC 4, SHA 1 p We don’t know how to distinguish the PRNG’s output from random, or compute state from output.
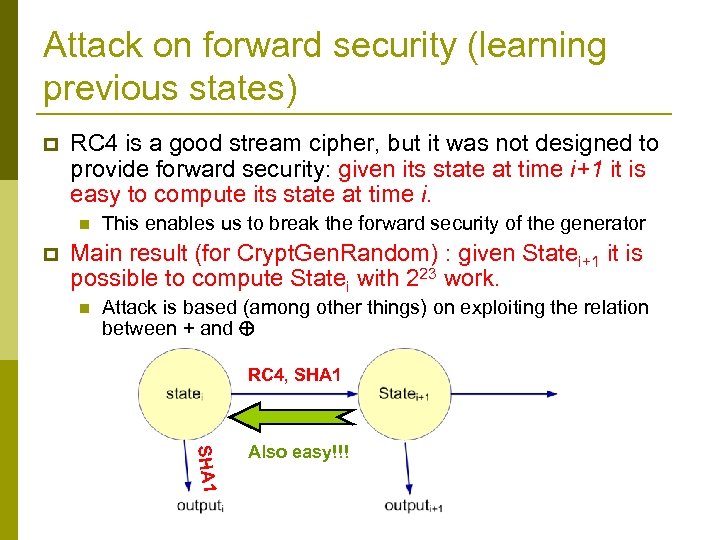
Attack on forward security (learning previous states) p RC 4 is a good stream cipher, but it was not designed to provide forward security: given its state at time i+1 it is easy to compute its state at time i. n p This enables us to break the forward security of the generator Main result (for Crypt. Gen. Random) : given Statei+1 it is possible to compute Statei with 223 work. n Attack is based (among other things) on exploiting the relation between + and RC 4, SHA 1 Also easy!!!

An even simpler attack on forward security p Suppose we know the initial values of State and R n n These variables are never initialized, but rather take whatever value is on the stack location in which they are stored. These values are quite predictable. Given current value of RC 4 state(s) we can rewind them to the initial values p Now, given initial values of all registers we can simulate the RNG. p

Implications p MSFT: “this is a local information disclosure vulnerability and has no possibility of code execution and cannot be accessed remotely. ” p But, n n New remote execution attacks are found every week. Our attack can be used to amplify their effect.
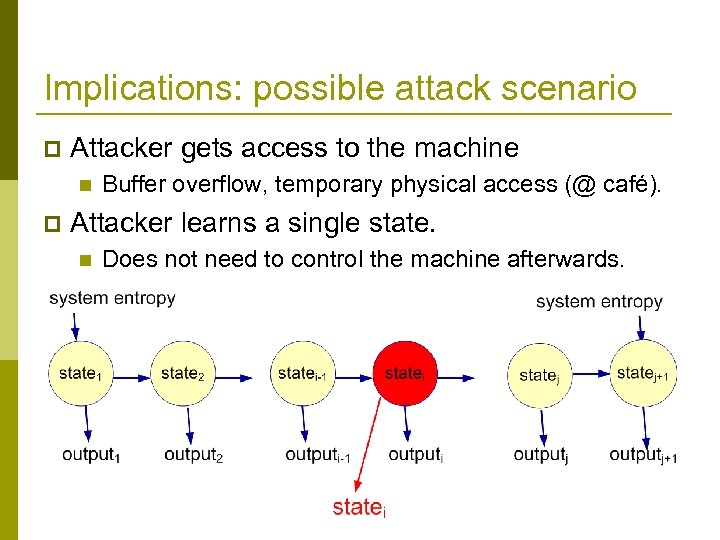
Implications: possible attack scenario p Attacker gets access to the machine n p Buffer overflow, temporary physical access (@ café). Attacker learns a single state. n Does not need to control the machine afterwards.
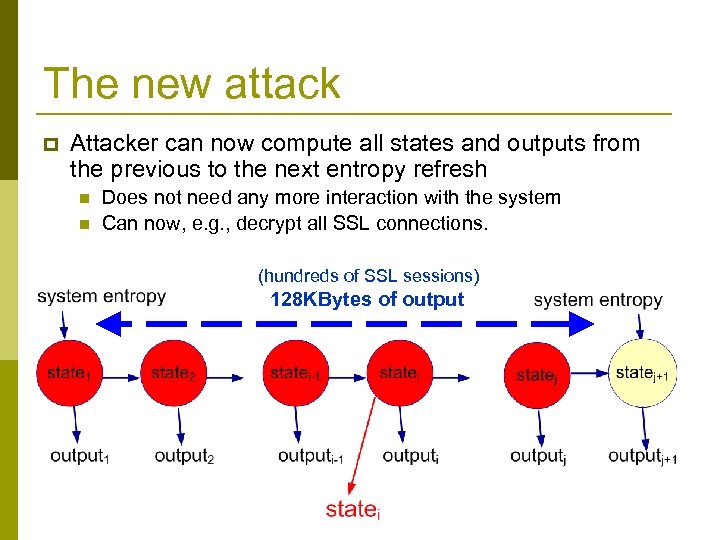
The new attack p Attacker can now compute all states and outputs from the previous to the next entropy refresh n n Does not need any more interaction with the system Can now, e. g. , decrypt all SSL connections. (hundreds of SSL sessions) 128 KBytes of output
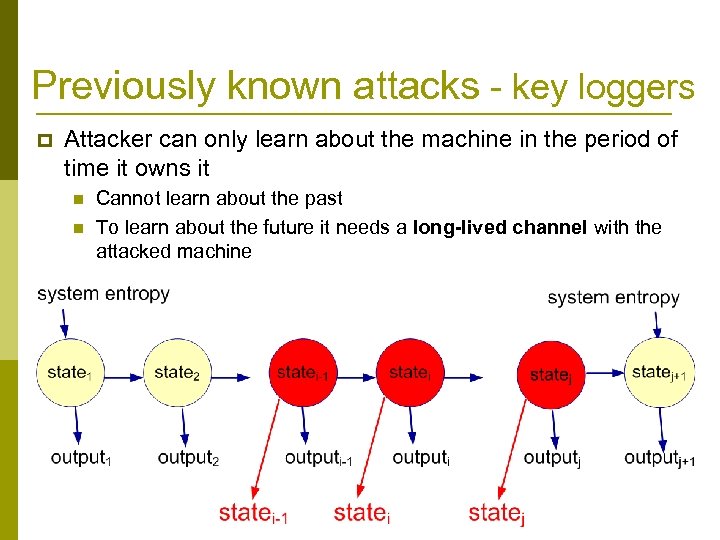
Previously known attacks - key loggers p Attacker can only learn about the machine in the period of time it owns it n n Cannot learn about the past To learn about the future it needs a long-lived channel with the attacked machine

The Attack on Forward Security
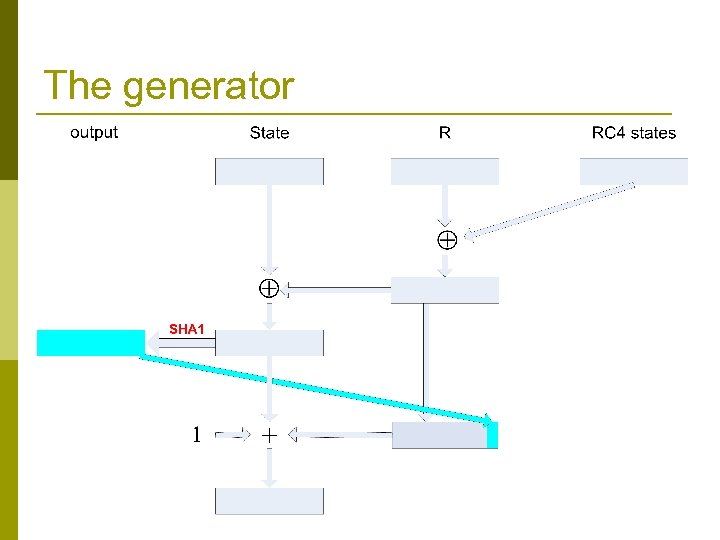
The generator
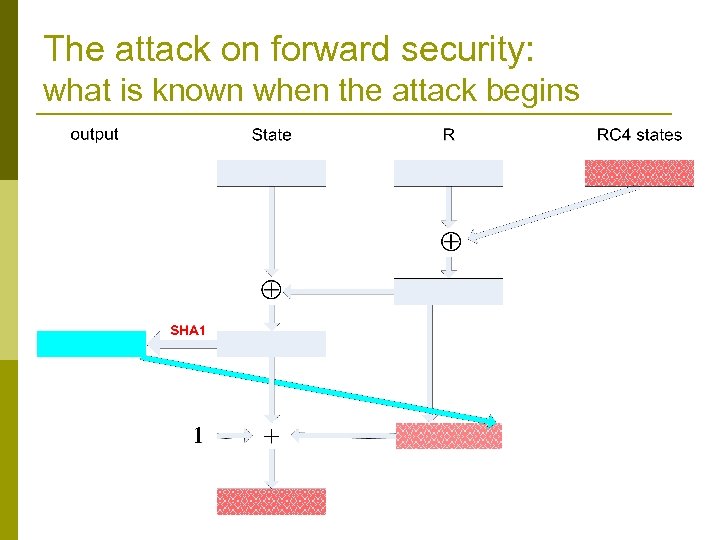
The attack on forward security: what is known when the attack begins
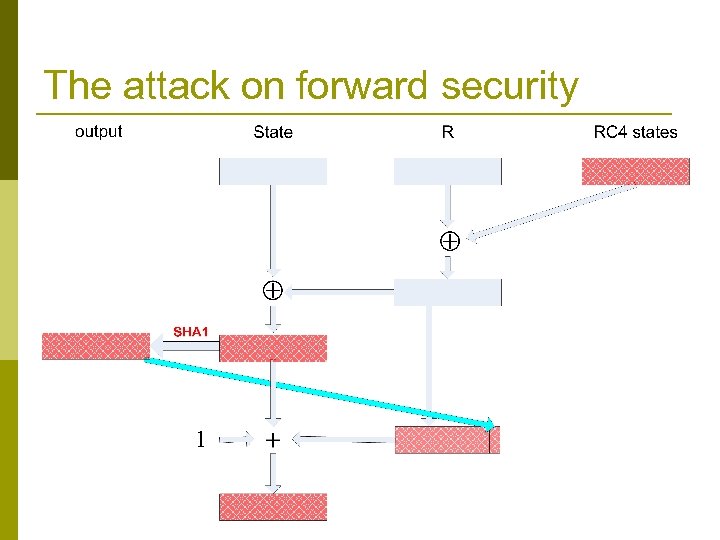
The attack on forward security
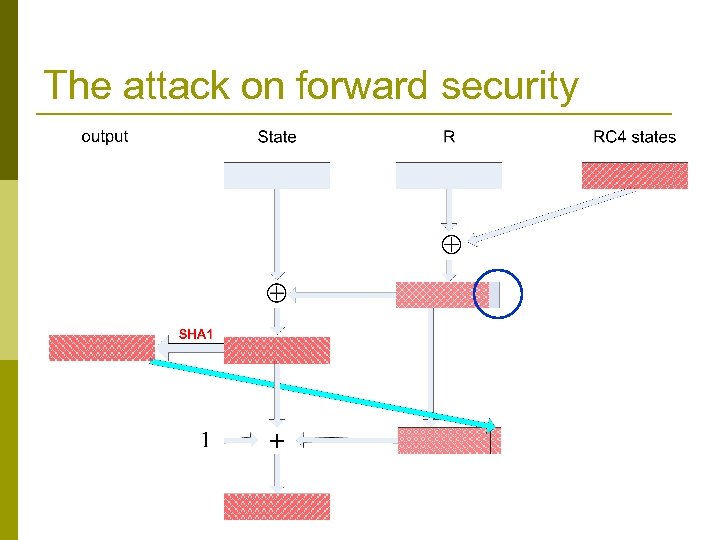
The attack on forward security
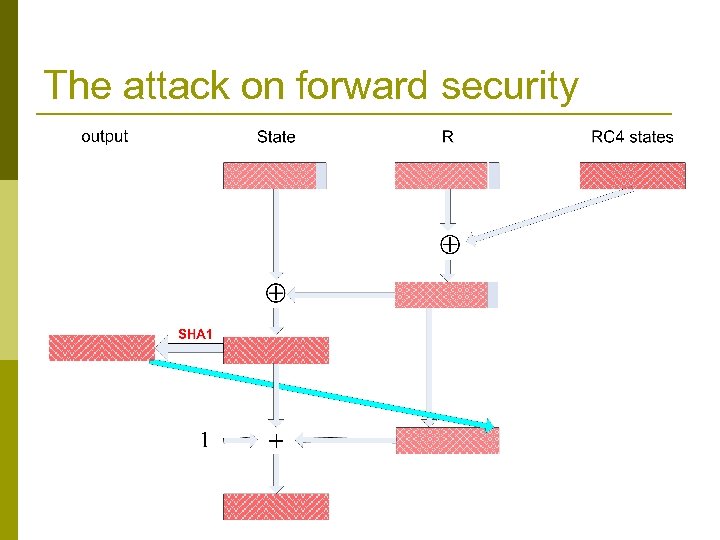
The attack on forward security
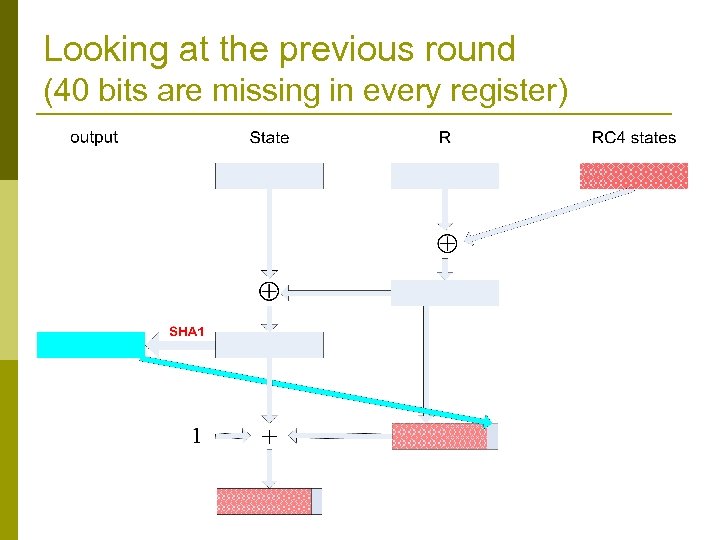
Looking at the previous round (40 bits are missing in every register)
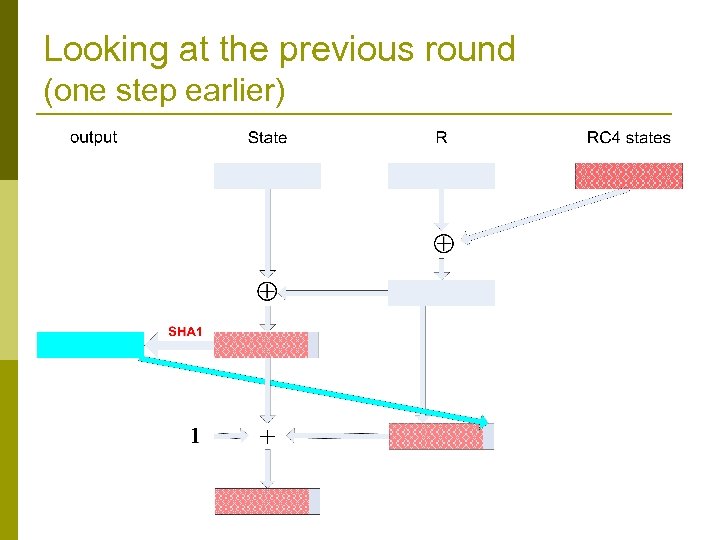
Looking at the previous round (one step earlier)
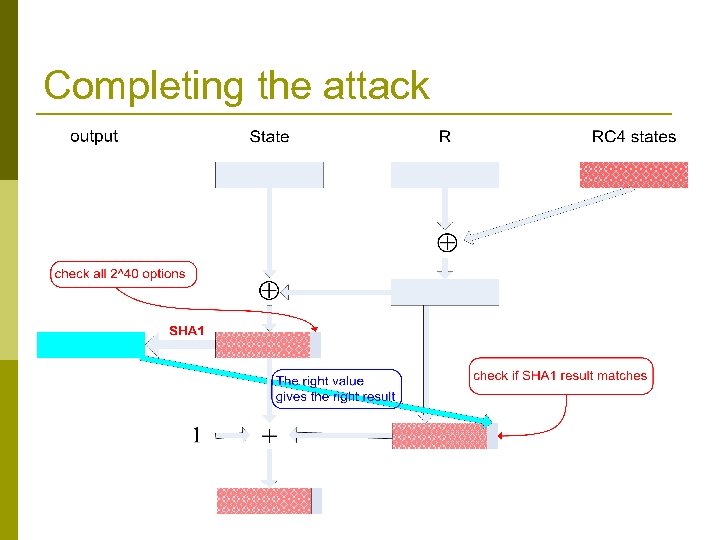
Completing the attack

False positives p p p The attack checks 240 options for the missing 5 bytes True value always gives a match. Each other value gives a (false positive) match with probability 2 -40. False positives are identified if they have no preimages. … t t-1 t-2 t-3 Not really a problem, since we expect O(k) false positive at time t-k (analysis using martingales).

Overhead of our attack p A simple attack requires 240 invocations of SHA 1 p A more intricate attack (using the relation between + and ) requires 223 work on average n n p Our implementation of this attack runs in 19 seconds (no optimization) Dag Arne Osvik implements SHA 1 on the Play. Station 3 Performs 83 Million SHA 1 invocations per second can implement our attack in 1/10 of a second! Details of improved attack on whiteboard.

What about XP p The external layer of the PRNG in XP is identical More complex than while (Len >0) { Windows 2000 R : = R System. Function 036() No forward security State : = State R here means no T : = SHA-1’( State ) forward security for Buffer : = Buffer | T the entire PRNG // | denotes concatenation R[0. . 4] : = T[0. . 4] // copy 5 least significant bytes State : = State + R + 1 Len : = Len − 20 }

News Flash! p MSFT’s first answer: “…(later versions of Windows) contain various changes and enhancements to the random number generator. ” p MSFT’s later answer: n n n XP is vulnerable to the attack. Vista, Windows Server 2008 and Windows Server 2003 SP 2 are not affected by the attack. The XP vulnerability will be fixed in SP 3.

Future work p Investigate other Windows OS’s n —— Vista, XP, Mobile. n In particular, examine the PRNG-OS interaction. p Recommendations: Switch to a design which supports forward security (e. g. , Barak-Halevi [ACM CCS 05], which provides theoretical guarantees). n Perform entropy rekeys more often (but not too often). n

Analysis of the Linux random number generator With Zvi Gutterman, Tzachy Reinman Hebrew University IEEE Symposium on Security and Privacy, 2006 Black Hat 2006

Linux PRNG (LRNG) p p p Development Started by Theodore Ts’o in 1994 Engineering: Implemented in the kernel. Complex structure, hundreds of patches to date, changes on a weekly base. Used by many applications n p TCP, PGP, SSL, S/MIME, … Two interfaces n n Kernel interface – get_random_bytes (non-blocking) User interfaces – /dev/random (blocking) “extremely secure” /dev/urandom (non-blocking)

On reverse engineering p p The Linux PRNG is part of the Linux kernel and hence its source is open The entire code is 2500 lines written in C The code is unclear, complex and constantly being patched. (Some major bugs took more than a year to be identified. ) Our tools n n p Static analysis Kernel modification: required many kernel builds, while ensuring that kernel changes do not affect generator entropy usage. We implemented and confirmed our findings with a user mode simulator.
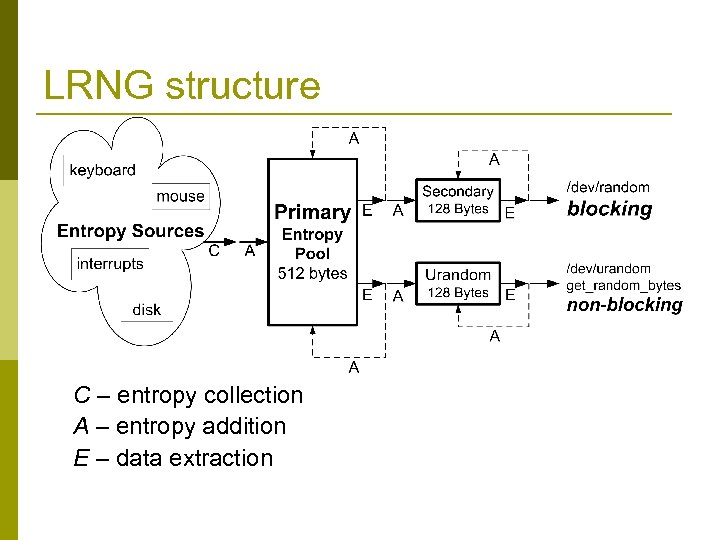
LRNG structure C – entropy collection A – entropy addition E – data extraction

Entropy Collection p p Asynchronous – entropy is constantly gathered and added to the pools (unlike Windows). Events are represented by two 32 -bit words: n Event type p n p Event time in milliseconds from up time Bad news: n n p E. g. , mouse press, keyboard value, HD id. Actual entropy in every event is very limited Most entropy comes from HD reads/writes. We conducted experiments which showed that each op contributes ~1 bit. Good news: n There are many events…

Comparison to Windows We showed an attack on forward security in Linux, but it is less efficient (264 vs. 223) p The implications of the attack are less severe (frequent entropy updates in Linux vs. infrequent updates in Windows) p Also, in Linux p n n n Generator is in kernel space Same generator used by all processes Blocking interface (/dev/random) Susceptible to Do. S attacks (even by remote attackers).

Implications to disk-less systems

Implications to disk-less systems p More and more systems are using solid state (flash) based storage instead of hard disks. n n p Other sources of entropy are quite limited: user input, system interrupts. n p The timing of HD r/w operations is unpredictable. Solid state operations always have the same timing. HD timing is the major source of entropy for the Linux PRNG. They might be guessed by an attacker. Possible threat to the security of the Linux PRNG in many future systems.

What can be done to seed the generator with more entropy? p Known recommendation: Linux PRNG should simulate continuity between shutdown and reboot n n p At shutdown 512 bytes are read from /dev/urandom. At reboot these bytes are written to the PRNG. An attacker that wants to guess the PRNG state must now record/guess all inputs and interrupts since the first run of the machine. This is done by the Linux distribution (not the kernel). But, Linux distributions on CD/DVD (Knoppix) cannot save the state. n Many other systems (e. g. , the Open. WRT Linux based router) do not save the state of their generator.

Analysis of a certain Linux based device p A surprising finding: The device always boots with one of 6 possible values of the PRNG state. n n p During reboot, the PRNG n n p The device uses solid state storage and no HD. The PRNG does not save its state at shutdown. Reads values from a hardware based noise generator. Copies the system clock onto its state. But, at that time n n Hardware noise generator provides non-random output. Hardware clock is not loaded to the software clock, so the value read from the software clock is always fixed.

Preliminary results p Can predict keys used by this device in SSH sessions, and decrypt communication n p If these sessions are initiated before an input from user is received Output of PRNG is a function of user’s input only n n n If we observe the output of the PRNG, can we deduce user’s input? Yes, if the user enters his input slowly enough! Can this be done by an external attacker?

Take-home message Be careful when designing (or using) devices without a hard-disk

Conclusions The security of the output of pseudo-random generators is crucial. p It is hard to examine OS based PRNGs p n n p The algorithms are not published. One must examine the code. This is not easy. Intricate dependencies with the OS – analyzing the algorithm alone is not enough. The generators of both Windows and Linux do not provide forward security n and have additional design issues

Conclusions p Most severe findings n The PRNGs of Windows XP/2000 do not provide forward security p n Affecting > 90% of all PCs Disk-less Linux systems

TODO p Windows n n p Examine other windows systems Understand the relation with the OS (initialization) Linux n Disk-less systems – many new attacks are possible p PRNG usage within a virtual machine? p Change the design of common PRNGs n Use the Barak-Halevi construction
19d9fbda0b6a9e21e3cd5a9bd30a19b8.ppt