c37d9e776ecaeefb99c7b9366817d893.ppt
- Количество слайдов: 14

On the Black Hole/Black Ring Transition Ernesto Lozano-Tellechea Weizmann Institute of Science Israel ICHEP-04 Beijing Based on colaboration with: Giovanni Arcioni (Hebrew University) [to appear]

Introduction • Subject: phase transitions in BH Physics • Black Hole Phases: – In 4 d: BH uniqueness – In d>4: different phases ( ↔ horizon topolgy) (BHs, black stings, branes…) Phase transitions between them?

BH Phase Transitions • Noncompact dimensions: Gregory-Laflamme Black String Black Hole • Compact Dimensions: Small BH ↔ Compact Black String • Relevance: – Gravitation: Cosmic Censorship, singularities, … [Kol, Harmark, Obers, Sorkin, Weiseman, … ] – Field Theory (Ad. S/CFT): Confinement/Deconfinement, … [Aharony, Gubser, Minwalla, Witten…]
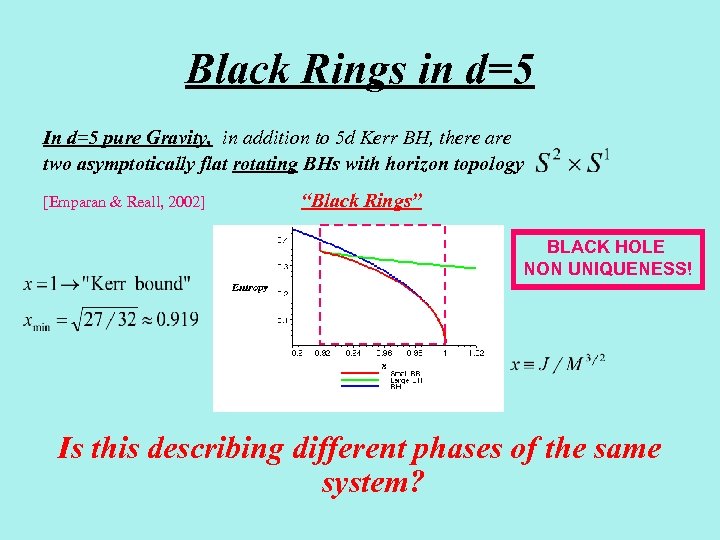
Black Rings in d=5 In d=5 pure Gravity, in addition to 5 d Kerr BH, there are two asymptotically flat rotating BHs with horizon topology [Emparan & Reall, 2002] “Black Rings” BLACK HOLE NON UNIQUENESS! Is this describing different phases of the same system?

Dynamical vs. Thermodynamical Stability • True question: dynamical stabilility Can it be derived from thermodynamics? [Davies ‘ 77] [Gubser & Mitra 2000] • In ordinary (extensive) systems: STABILITY ↔ ( positivity of the Hessian of S) NOT APPLICABLE TO BHs !! (prime example: Schwarzschild BH)

In this talk: We will try to address the issues of Stability Study of critical points in the Black Hole/Black Ring system using appropriate tools for the study of non-extensive thermodynamics

Stability of Non-Extensive Systems • Let us use only the entropy-max principle: [“Poincare method” of stability] [Katz ‘ 79] [Kaburaki ‘ 94] Stability of the Lorentzian solution ↔ Microcanonical ensemble (fixed M, fluctuations in Temperature) Equilibrium series S(M) Near the equilibrium series: Off-Equilibrium (Natural extension: Legendre Transform)
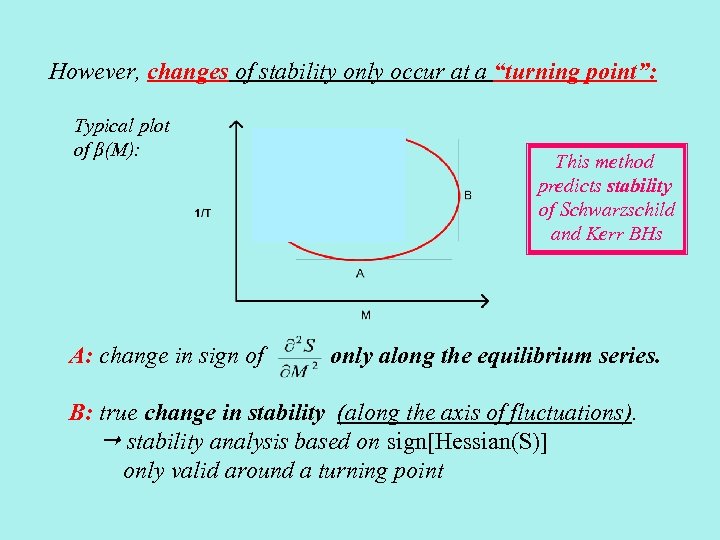
However, changes of stability only occur at a “turning point”: Typical plot of β(M): A: change in sign of This method predicts stability of Schwarzschild and Kerr BHs only along the equilibrium series. B: true change in stability (along the axis of fluctuations). stability analysis based on sign[Hessian(S)] only valid around a turning point
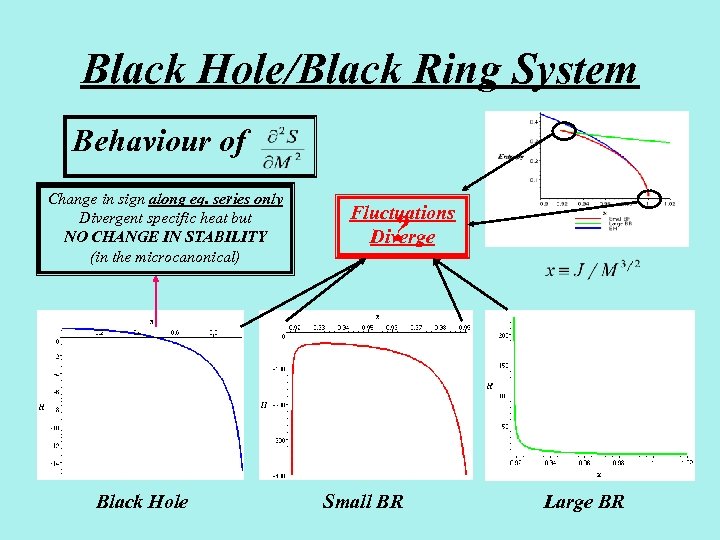
Black Hole/Black Ring System Behaviour of Change in sign along eq. series only Divergent specific heat but NO CHANGE IN STABILITY (in the microcanonical) Black Hole Fluctuations Diverge ? Small BR Large BR
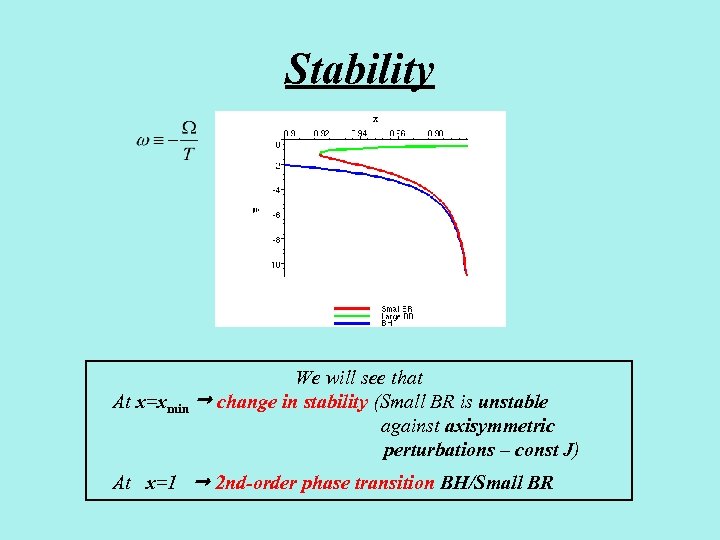
Stability We will see that At x=xmin change in stability (Small BR is unstable against axisymmetric perturbations – const J) At x=1 2 nd-order phase transition BH/Small BR

Critical Exponents • One can define the appropriate susceptibilities • And order parameter Obey scaling relations of the “first kind” What about the correlation length and scalings of the both at: ↔ “second BH/SBR kind”? ↔ SBR/LBR

Thermodynamic Geometry • Proposal: Allows to compute ξ and check scalings of the 2 nd kind [Ruppeiner ‘ 79] Suitable for nonextensive thermodynamics
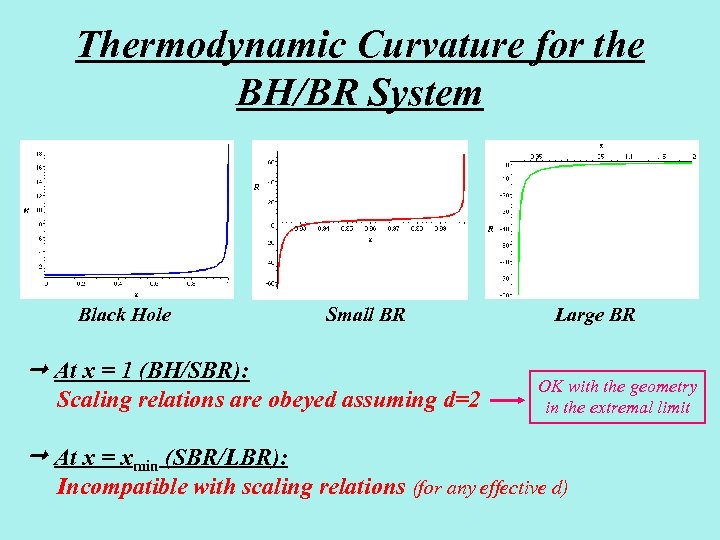
Thermodynamic Curvature for the BH/BR System Black Hole Small BR At x = 1 (BH/SBR): Scaling relations are obeyed assuming d=2 At x = xmin (SBR/LBR): Large BR OK with the geometry in the extremal limit Incompatible with scaling relations (for any effective d)
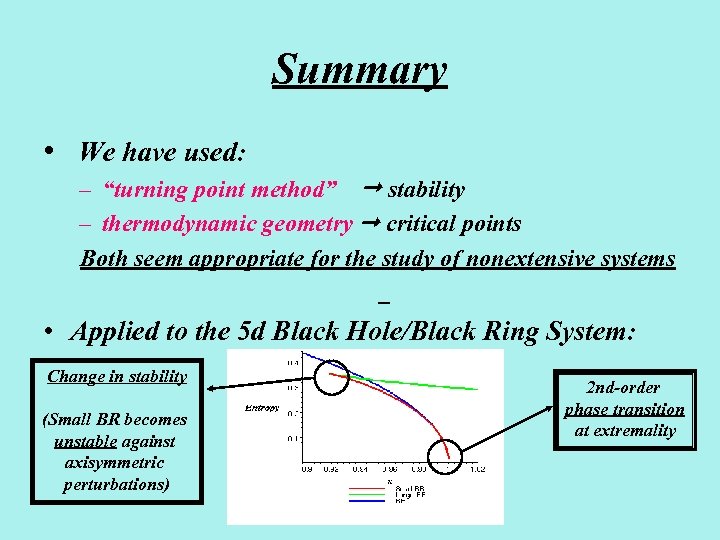
Summary • We have used: – “turning point method” stability – thermodynamic geometry critical points Both seem appropriate for the study of nonextensive systems • Applied to the 5 d Black Hole/Black Ring System: Change in stability (Small BR becomes unstable against axisymmetric perturbations) 2 nd-order phase transition at extremality
c37d9e776ecaeefb99c7b9366817d893.ppt