On Schema Matching with Opaque Column Names and

On Schema Matching with Opaque Column Names and Data Values Jaewoo Kang NC State (Aug 2003) Jeffrey F. Naughton June 10, 2003 Univ. of Wisconsin-Madison SIGMOD 2003

What is Schema Matching? n n Finding semantic correspondences of schema elements across heterogeneous sources. Old problem yet attracting new interests. SIGMOD 2003 June 10, 2003 2 Jaewoo Kang

What is Schema Matching? (Cont’d) n Important for enterprise applications n n Also important for Internet data n n Data warehouses, data migration. Virtual databases, web information systems. Fundamental element of data integration. SIGMOD 2003 June 10, 2003 3 Jaewoo Kang

No Silver Bullet! n n State of the art: A collection of techniques that propose matches. We have added a new technique to this collection that works when previous techniques don’t even apply. SIGMOD 2003 June 10, 2003 4 Jaewoo Kang

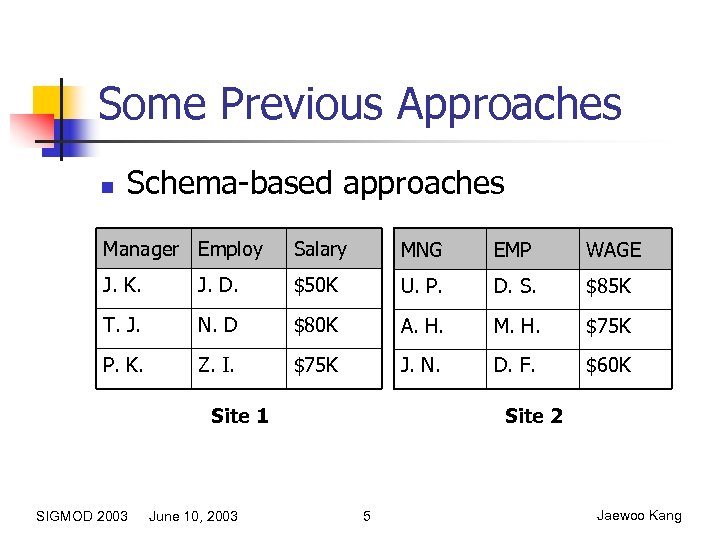Some Previous Approaches n Schema-based approaches Manager Employ Salary MNG EMP WAGE J. K. J. D. $50 K U. P. D. S. $85 K T. J. N. D $80 K A. H. M. H. $75 K P. K. Z. I. $75 K J. N. D. F. $60 K Site 1 SIGMOD 2003 June 10, 2003 Site 2 5 Jaewoo Kang

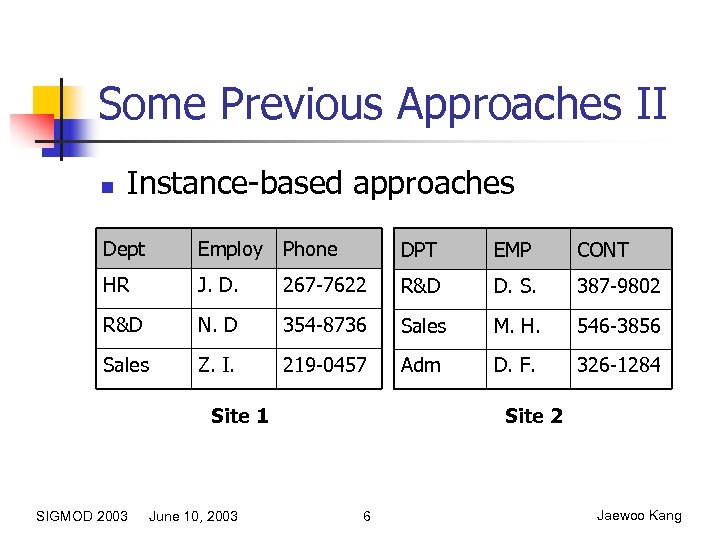Some Previous Approaches II n Instance-based approaches Dept Employ Phone DPT EMP CONT HR J. D. 267 -7622 R&D D. S. 387 -9802 R&D N. D 354 -8736 Sales M. H. 546 -3856 Sales Z. I. 219 -0457 Adm D. F. 326 -1284 Site 1 SIGMOD 2003 June 10, 2003 Site 2 6 Jaewoo Kang

So two previous approaches n n Schema-based (interpret column names) Instance-based (interpret data values) SIGMOD 2003 June 10, 2003 7 Jaewoo Kang

But what about this problem? t 1 t 2 t 3 t 4 t 5 t 6 t 7 193 7. 3 3. 6 5. 7 9 0. 39 0. 2 164 7. 4 4. 2 3. 8 13 0. 57 0. 4 176 7 4. 5 8 15 0. 87 0. 4 129 6. 3 3. 4 4. 8 16 0. 44 0. 2 123 6. 3 3. 8 7 12 0. 56 0. 5 136 7. 6 4 3. 1 9 0. 52 0. 6 238 6. 7 3. 9 3. 7 18 0. 44 0. 5 395 6. 9 3. 6 4. 8 8 0. 38 0. 4 174 6. 1 3. 5 4. 4 21 0. 56 0. 6 93 6. 6 3. 7 3. 9 17 0. 61 0. 6 96 6. 1 4. 1 3. 1 10 0. 73 0. 3 114 6. 8 3. 9 4 17 0. 32 0. 5 133 8. 4 4. 7 6. 3 12 0. 77 0. 3 144 7. 8 4. 3 3. 8 16 0. 51 0. 9 Site 1 SIGMOD 2003 June 10, 2003 Site 2 8 Jaewoo Kang

This is the “Un-interpreted Matching” Problem. n n Focus of this talk Outline of the remainder of this talk n n SIGMOD 2003 Formal definition Terminology Algorithm Experimental Results June 10, 2003 9 Jaewoo Kang

Un-interpreted Matching M 1 = match(R(r 1, r 2, . . , rn), S(s 1, s 2, . . , sm)) M 2 = match(R(r 1, r 2, . . , rn), S’(f 1(s 1), f 2(s 2), . . , fm(sm)) where match = a schema matching algorithm, Mi = {(ri-sj)} : set of matching column pairs, fi = arbitrary one-to-one function. ‘match’ is an un-interpreted matching iff M 1=M 2 for all fi’s. n Main idea: specific token representing column name and value is not important. SIGMOD 2003 June 10, 2003 10 Jaewoo Kang

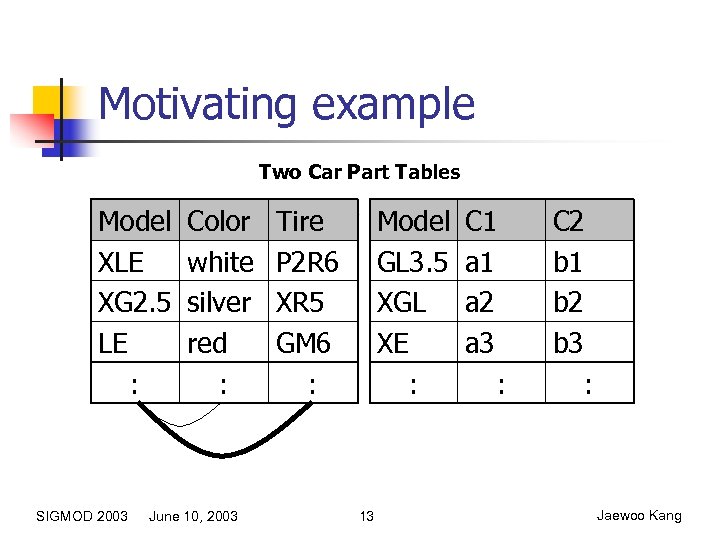
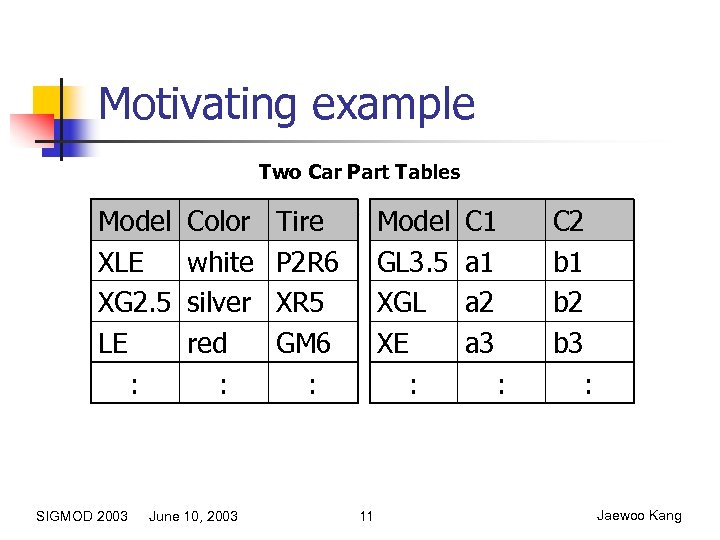Motivating example Two Car Part Tables Model XLE XG 2. 5 LE : SIGMOD 2003 Color white silver red : June 10, 2003 Tire P 2 R 6 XR 5 GM 6 : Model GL 3. 5 XGL XE : 11 C 1 a 2 a 3 : C 2 b 1 b 2 b 3 : Jaewoo Kang

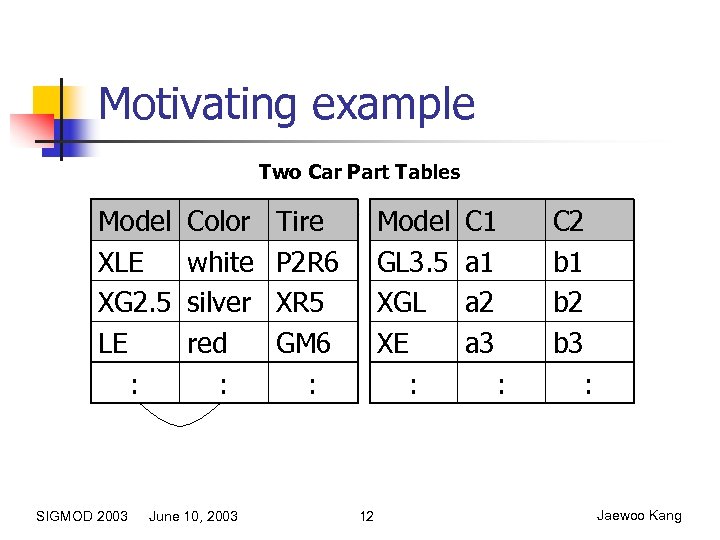Motivating example Two Car Part Tables Model XLE XG 2. 5 LE : SIGMOD 2003 Color white silver red : June 10, 2003 Tire P 2 R 6 XR 5 GM 6 : Model GL 3. 5 XGL XE : 12 C 1 a 2 a 3 : C 2 b 1 b 2 b 3 : Jaewoo Kang

Motivating example Two Car Part Tables Model XLE XG 2. 5 LE : SIGMOD 2003 Color white silver red : June 10, 2003 Tire P 2 R 6 XR 5 GM 6 : Model GL 3. 5 XGL XE : 13 C 1 a 2 a 3 : C 2 b 1 b 2 b 3 : Jaewoo Kang

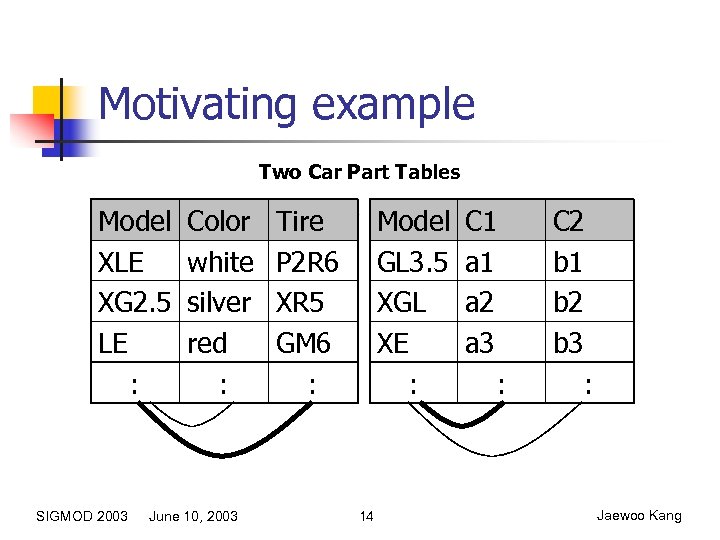Motivating example Two Car Part Tables Model XLE XG 2. 5 LE : SIGMOD 2003 Color white silver red : June 10, 2003 Tire P 2 R 6 XR 5 GM 6 : Model GL 3. 5 XGL XE : 14 C 1 a 2 a 3 : C 2 b 1 b 2 b 3 : Jaewoo Kang

Background n Before introducing our algorithm, need: n n SIGMOD 2003 Information Entropy Mutual Information Modeling Dependency Relations Graph Matching June 10, 2003 15 Jaewoo Kang

Information Entropy n n Measures the uncertainty of values in an attribute Standard information theoretic measure SIGMOD 2003 June 10, 2003 16 Jaewoo Kang

Mutual Information n Another standard information theoretic measure Measures the amount of information captured in one attribute about the other. Note Self-information MI(X; X) = H(X) SIGMOD 2003 June 10, 2003 17 Jaewoo Kang

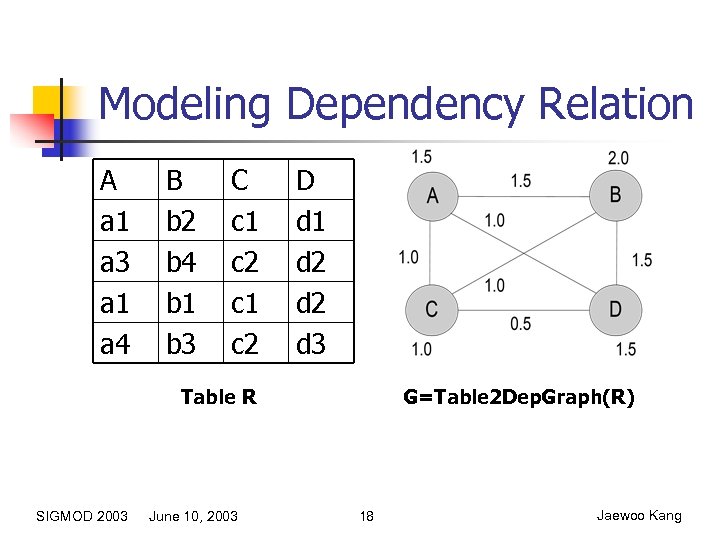Modeling Dependency Relation A a 1 a 3 a 1 a 4 B b 2 b 4 b 1 b 3 C c 1 c 2 D d 1 d 2 d 3 Table R SIGMOD 2003 June 10, 2003 G=Table 2 Dep. Graph(R) 18 Jaewoo Kang

Graph Matching G 1 n n n G 2 Our algorithm will use graph matching. {(G 1(a), G 2(b))}=Graph. Match(G 1, G 2) Finds a mapping that minimizes the distance between the two graphs. SIGMOD 2003 June 10, 2003 19 Jaewoo Kang

Distance Between the Graphs n Euclidean distance metric (Frobenius norm) n n SIGMOD 2003 where aij and bij = mutual information between node i and j. m(node in A) = matching node in B. June 10, 2003 20 Jaewoo Kang

Measuring the quality of match results SIGMOD 2003 June 10, 2003 21 Jaewoo Kang

Finally, Our Matching Algorithm 1. G 1 = Table 2 Dep. Graph(S 1); G 2 = Table 2 Dep. Graph(S 2); 2. {(G 1(a), G 2(b))} = Graph. Match(G 1, G 2); where Si = an input table, Gi = a dependency graph, (G 1(a), G 2(b)) = a matching node pair. SIGMOD 2003 June 10, 2003 22 Jaewoo Kang

Validating the Framework n Graph matching algorithm n n n Used exhaustive search w/ simple filtering. Can be replaced w/ approximate algorithms in practice. System n SIGMOD 2003 Java Hot. Spot VM 1. 4 June 10, 2003 23 Jaewoo Kang

Goals of experiments… n n Main goal: see if mutual informationbased un-interpreted matching works. Secondary goal: see if mutual information is necessary, or if a simpler approach, Entropy-only Matching, works just as well. n SIGMOD 2003 Only compares the entropies of attributes in isolation, without considering mutual information. June 10, 2003 24 Jaewoo Kang

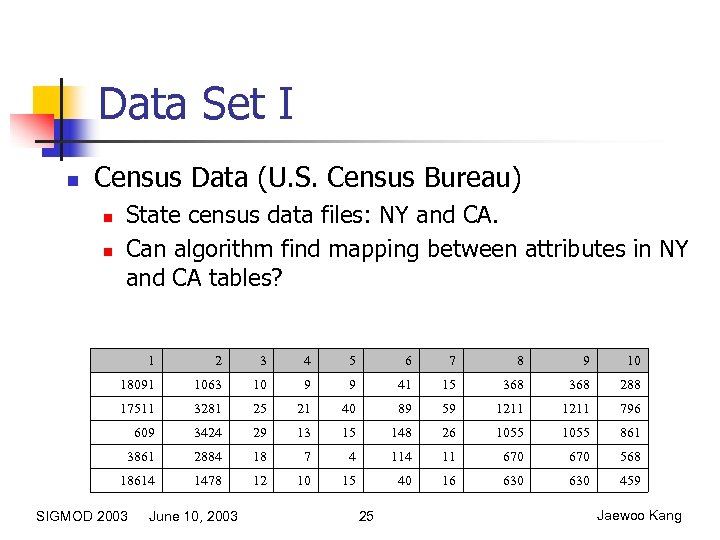Data Set I n Census Data (U. S. Census Bureau) n n State census data files: NY and CA. Can algorithm find mapping between attributes in NY and CA tables? 1 2 3 4 5 6 7 8 9 10 18091 1063 10 9 9 41 15 368 288 17511 3281 25 21 40 89 59 1211 796 609 3424 29 13 15 148 26 1055 861 3861 2884 18 7 4 11 670 568 18614 1478 12 10 15 40 16 630 459 SIGMOD 2003 June 10, 2003 25 Jaewoo Kang

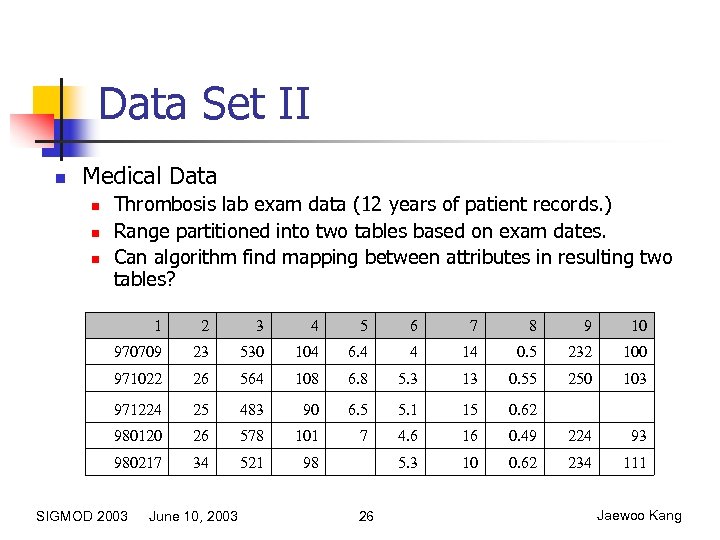Data Set II n Medical Data n n n Thrombosis lab exam data (12 years of patient records. ) Range partitioned into two tables based on exam dates. Can algorithm find mapping between attributes in resulting two tables? 1 2 3 4 5 6 7 8 9 10 970709 23 530 104 6. 4 4 14 0. 5 232 100 971022 26 564 108 6. 8 5. 3 13 0. 55 250 103 971224 25 483 90 6. 5 5. 1 15 0. 62 980120 26 578 101 7 4. 6 16 0. 49 224 93 980217 34 521 98 5. 3 10 0. 62 234 111 SIGMOD 2003 June 10, 2003 26 Jaewoo Kang

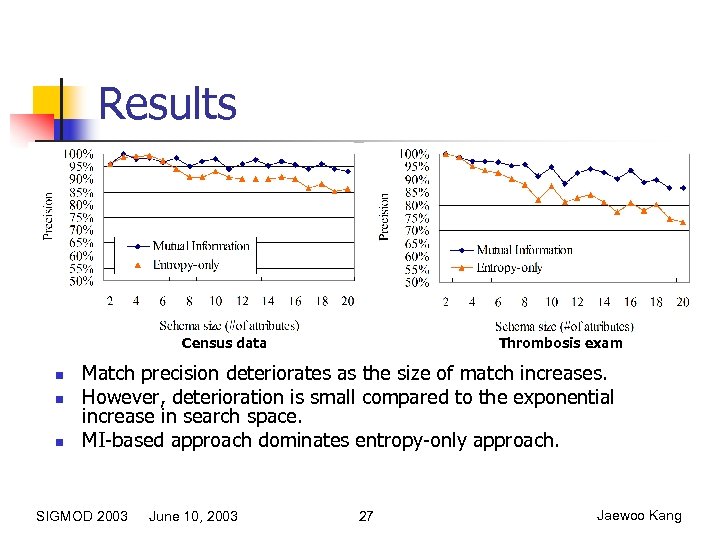Results Census data n n n Thrombosis exam Match precision deteriorates as the size of match increases. However, deterioration is small compared to the exponential increase in search space. MI-based approach dominates entropy-only approach. SIGMOD 2003 June 10, 2003 27 Jaewoo Kang

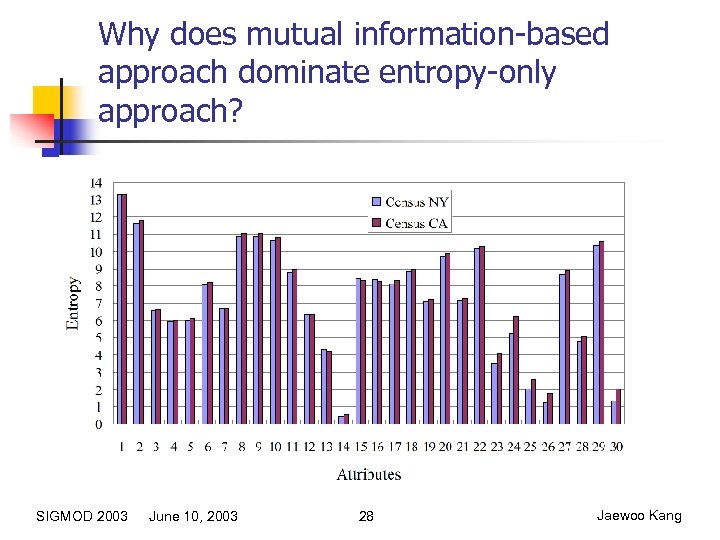Why does mutual information-based approach dominate entropy-only approach? SIGMOD 2003 June 10, 2003 28 Jaewoo Kang

Cardinality Constraints in Schema Matching n One-to-one mapping (bijective) A SIGMOD 2003 June 10, 2003 B B C G 1 A C 29 G 2 Jaewoo Kang

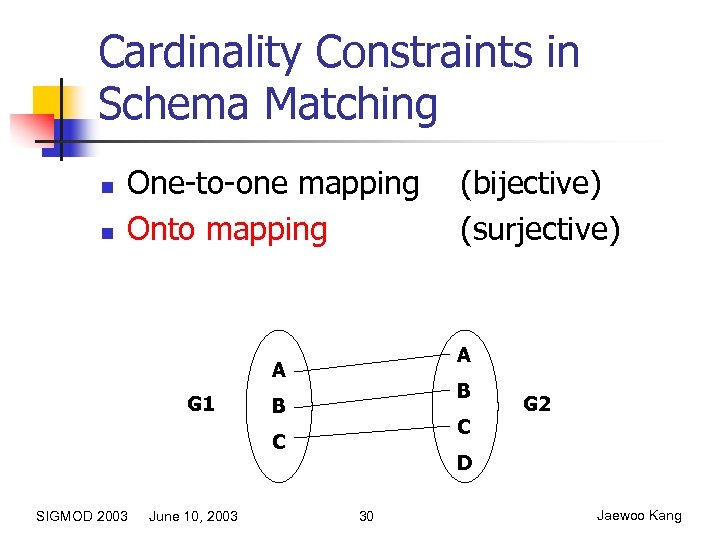Cardinality Constraints in Schema Matching n n One-to-one mapping Onto mapping A A G 1 B B C C SIGMOD 2003 June 10, 2003 (bijective) (surjective) G 2 D 30 Jaewoo Kang

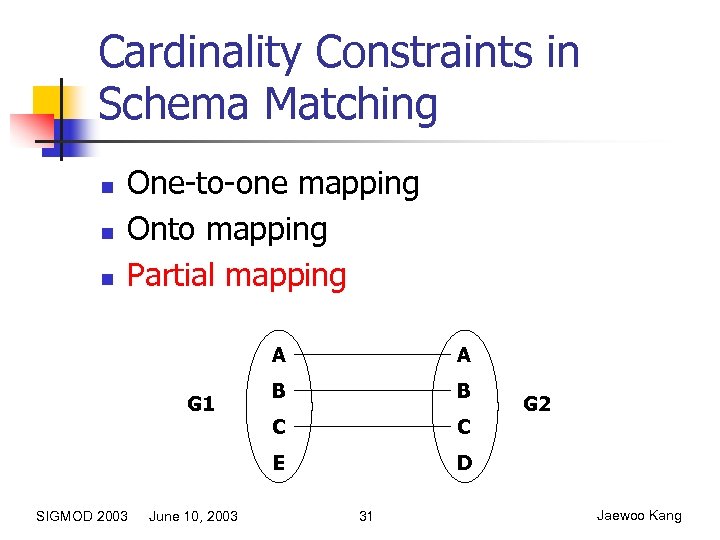Cardinality Constraints in Schema Matching n n n One-to-one mapping Onto mapping Partial mapping A SIGMOD 2003 June 10, 2003 B B C C E G 1 A D 31 G 2 Jaewoo Kang

What about schemas that don’t match? n Examined how our matching algorithm reacts to the matching of unrelated schemas. (NY-CA vs. Lab 1 -CA) SIGMOD 2003 June 10, 2003 32 Jaewoo Kang

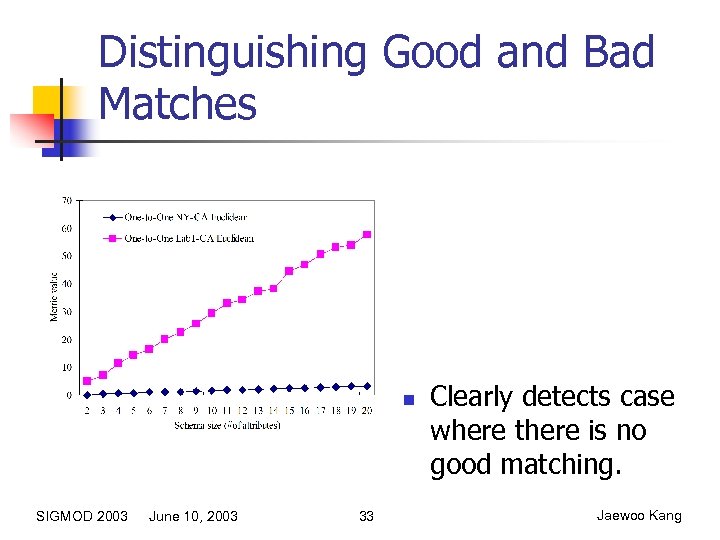Distinguishing Good and Bad Matches n SIGMOD 2003 June 10, 2003 33 Clearly detects case where there is no good matching. Jaewoo Kang

Summary n n n Identified new class of schema matching problems that have not been addressed by existing solutions. First to introduce an un-interpreted matching technique that addresses the new class of problems. Evaluation suggests it may be useful as an addition to existing matching techniques. SIGMOD 2003 June 10, 2003 34 Jaewoo Kang

Future Work n n n Find an efficient, accurate graph matching approximation algorithm. Extend the techniques to nested structures such as XML, OO schemas. See if the technique applicable to the problems of schema classification / clustering. SIGMOD 2003 June 10, 2003 35 Jaewoo Kang

Questions? n For more information: n n SIGMOD 2003 jaewoo@cs. wisc. edu http: //www. cs. wisc. edu/~jaewoo June 10, 2003 36 Jaewoo Kang