6f8ce30f580a7791d0dd5dd5eb5e4ac6.ppt
- Количество слайдов: 39

On Partitioning and Symbolic Model Checking FM 2005 Subramanian Iyer, UT-Austin Debashis Sahoo, Stanford E. Allen Emerson, UT-Austin Jawahar Jain, Fujitsu Labs

Outline Background The Partitioning Approach Model Checking n n n The naïve algorithm An improved algorithm Experiments and Conclusion

Outline Background The Partitioning Approach Model Checking n n n The naïve algorithm An improved algorithm Experiments and Conclusion

Sequential Verification n Does Implementation fullfil its Specification? n Model Checking: n n State Based Given: System under test Prove: properties given in a temporal logic (eg: CTL, LTL) Required for Model Checking: n Input Data : Transition relation n Generated : Reachable states, Forbidden states n Procedures : Boolean Operations, Image Computation

Reachability Analysis Algorithm: From=Reached=S 0 do{ To = Img(TR, From) New = To Reached = Reached + To From = New }while(New Ø ) Simple property: 2 n MC S 0 MD

Model Checking n Hinges on Reachability n n In Simple terms n n n Basic Operation: Pre-image Given “bad” formula f Compute reachable states Compute states satisfying f Pass if intersection is empty Key issues : State set generation and representation n n Extensional, as originally proposed. Symbolic, as now practiced
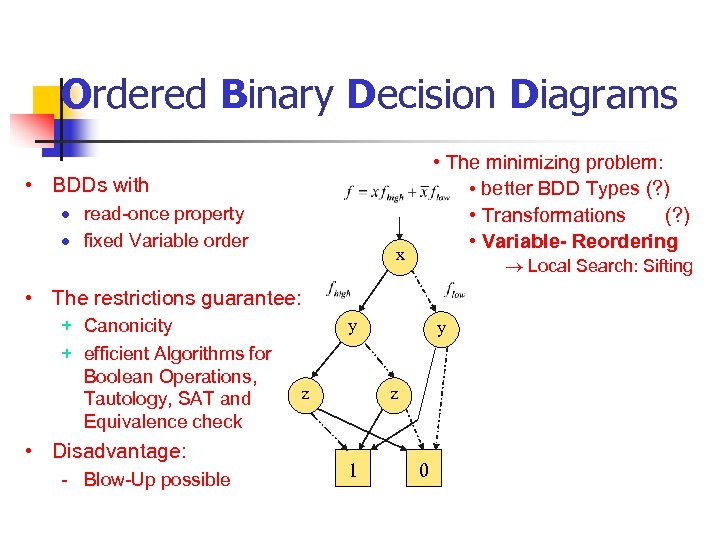
Ordered Binary Decision Diagrams • The minimizing problem: • better BDD Types (? ) • Transformations (? ) • Variable- Reordering • BDDs with · read-once property · fixed Variable order x ® Local Search: Sifting • The restrictions guarantee: + Canonicity + efficient Algorithms for Boolean Operations, Tautology, SAT and Equivalence check • Disadvantage: - Blow-Up possible y z

Symbolic Model Checking n Using BDDs to represent sets of states n Key operation is image computation n n Using transition relation Necessary to succinctly represent the transition relation What is the problem?

The Bottleneck in Verification State-based verification, model checking n Can be fully automated in principle Why not in practice? n State space representation n Symbolically manifests as “BDD blowup” n n n Limits extent of automation Limits size of designs that can be handled Capacity is restricted by representation size n n Memory restricts time BDD based tools – crash or thrash So What can be done?

Outline Background The Partitioning Approach Model Checking n n n The naïve algorithm An improved algorithm Experiments and Conclusion

Partitioned Transition Relation n Represented as conjunction of k parts TRi Easy to construct for synchronous circuits Conjunction of “bitwise” TRi’s – the transition function of each state variable n n n Set of variables partitioned into k disjoint subsets Transition functions for variables in each subset are conjuncted together to give TRi TR is the implicit conjunction of TRi for i in 1 to k
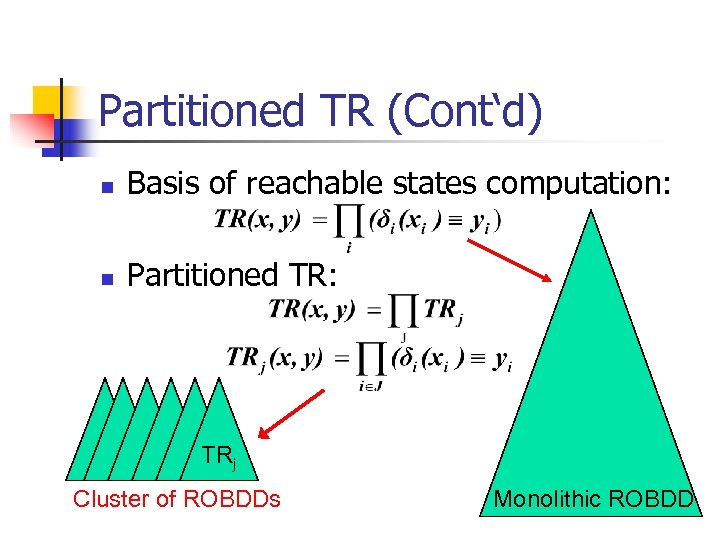
Partitioned TR (Cont‘d) n Basis of reachable states computation: n Partitioned TR: TRj Cluster of ROBDDs Monolithic ROBDD

Image Computation n The image computation step: Img(TR, A)= $x( TR(x, y) A(x)) n Partitioned TR useful due to quantification (And. Exist): early Img(TR, A)= $xn( TRn . . . $x 2( TR 2 $x 1( TR 1 A))). . . ) n Choice and order of TRj’s is crucial for a good performance!

Partitioned TR - Observations n What is it that is partitioned? n n The set of variables The relation Actual TR is an implicit conjunction Sets of states always ROBDD n n During image computation Before and After image computation

So What? n Sets of states as ROBDDs n n Can get very large TR parts repeatedly conjuncted n n During each image Made easier combined with quantification n n Still repeated expense Solution: Partition all state-sets

Partitioned ROBDD (POBDD) Given the Boolean Function Xf is its partitioned-ROBDD representation if, f where and are ROBDDs with variable ordering pi, and, w 1 w 2 f^ 1 f^ 2 Each wi is called a window function Note that the ROBDDs in each partition may have a different variables ordering pi f^ 4 w 4 ^ f 3 w 3
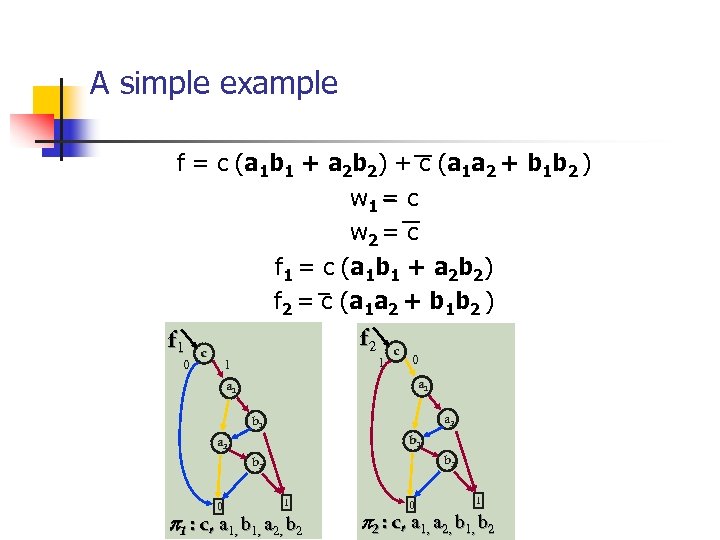
A simple example f = c (a 1 b 1 + a 2 b 2) + c (a 1 a 2 + b 1 b 2 ) w 1 = c w 2 = c f 1 = c (a 1 b 1 + a 2 b 2) f 2 = c (a 1 a 2 + b 1 b 2 ) f 2 c f 1 c c a 1 a 2 b 2 0 1 1 : c, a 1, b 1, a 2, b 2 0 1 2 : c, a 1, a 2, b 1, b 2

On Using Partitioning n Sets of states disjunctively partitioned n n n Induces disjunctive partitioning on TR n n TR is a Relation on state pairs: Quadratic Notice each such TRij can further be n n Key : Use same partitioning windows In particular, set of reachable states Monolithic, Disjunctive, or Conjunctive Image computation n Must consider to and from set in each partition

Reachability Revisited Old Algorithm: From=Reached=S 0 do{ To = Img(TR, From) New = To Reached += To From = New }while(New Ø ) Notice that From is now partitioned TR applied to Fromi of partition i, result Toi is also partitioned So Toij is owned by partition j Must be given to j. Quadratic such transfers!

Image and Reachability n Fix point computations performed n n n On each partition locally Using TRii Use reachability algorithm on ROBDDs Synchronization between partitions n n n Cross-over images finds states use TRij , Must keep it infrequent Postponed till local fixpoint reached .
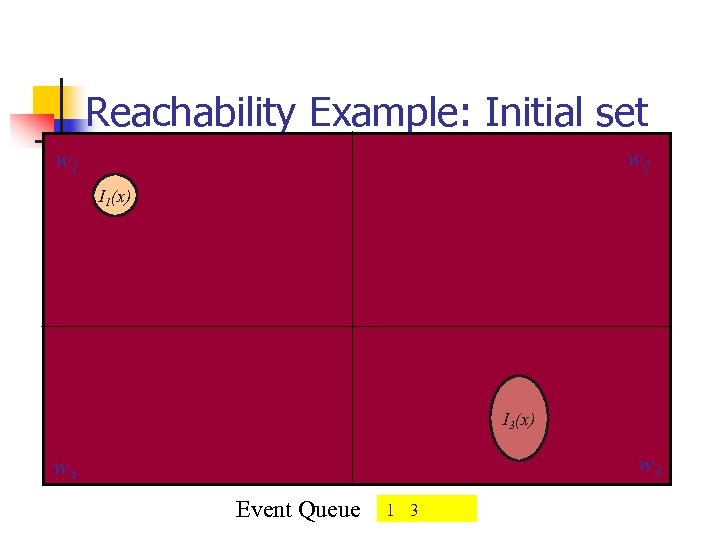
Reachability Example: Initial set w 2 w 1 I 1(x) I 3(x) w 3 w 4 Event Queue 1 3
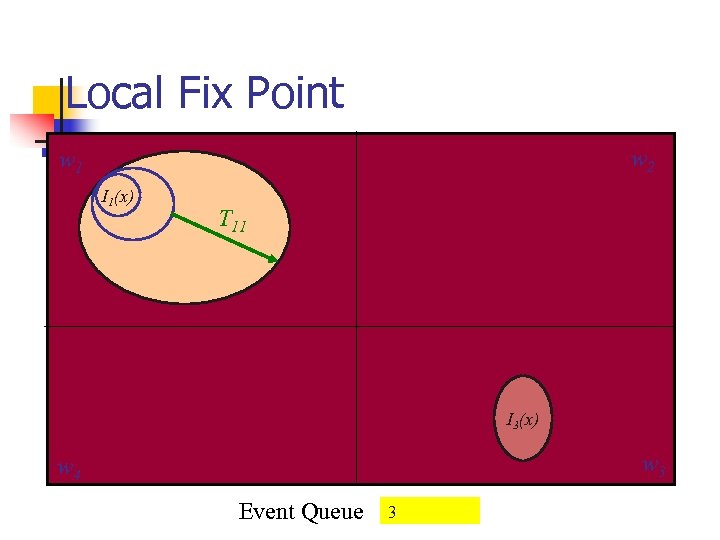
Local Fix Point w 2 w 1 I 1(x) T 11 I 3(x) w 3 w 4 Event Queue 3
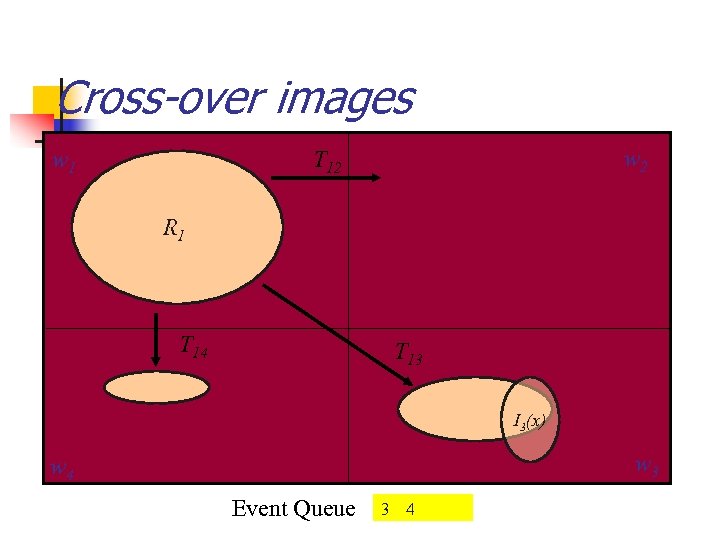
Cross-over images w 1 w 2 T 12 R 1 T 14 T 13 I 3(x) w 3 w 4 Event Queue 3 4
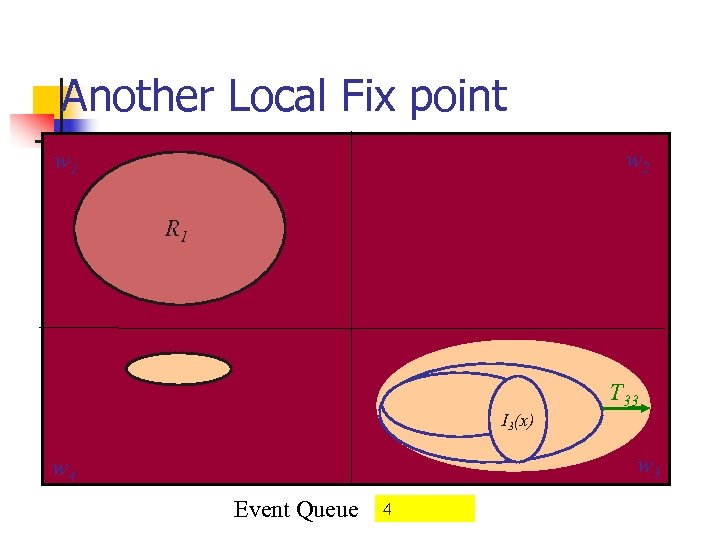
Another Local Fix point w 2 w 1 R 1 T 33 I 3(x) w 3 w 4 Event Queue 4
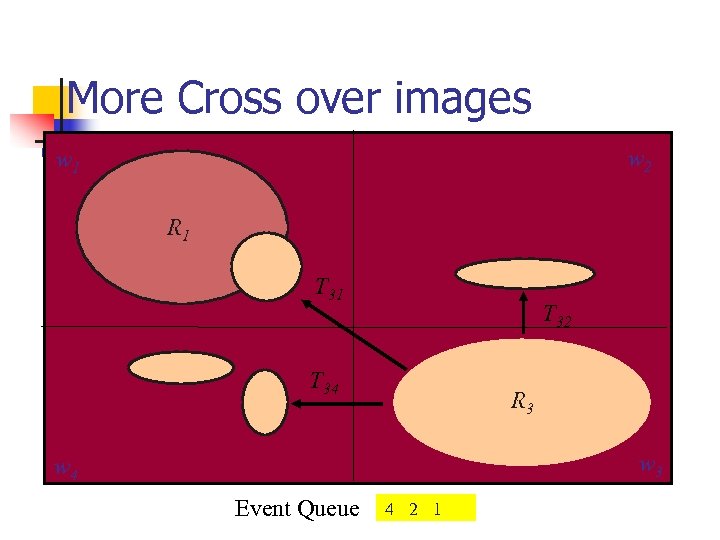
More Cross over images w 2 w 1 R 1 T 32 T 34 R 3 w 4 Event Queue 4 2 1
Example, cont. w 2 w 1 R 1 T 44 w 4 R 3 w 3 Event Queue 2 1

Outline Background The Partitioning Approach Model Checking n n n The naïve algorithm An improved algorithm Experiments and Conclusion

CTL : temporal properties n EX(f), E(f. Ug), EG(f) form a basis set n n Invariant Checking AGp Absence of Deadlock n n n Return to reset state AGEF(s 0) Temporal Implication AG(p EF q) Liveness EGp, AFp

Outline Background The Partitioning Approach Model Checking n n n The naïve algorithm An improved algorithm Experiments and Conclusion

Image Computation EXp n forall (partitions j) n forall (partitions k) n n Pre. Img_jk(s) = ∃s′, i[TRjk(s, s′, i) ∧ pk(s′)] reorder BDD Pre. Imgjk from part order k to j end for n Sj = ∨k Pre. Imgjk end for n output S

Least Fix Point E(p. Uq) n n S : = q , S. old : = NULL repeat n n n S. old : = S temp : = compute. EX(S) forall (partitions j) n Sj : = qj ∨ (pj ∧ tempj) end for until(S = S. old) n output S

Greatest Fix Point EGp n n S : = p repeat n n n S. old : = S temp : = compute. EX(S) forall (partitions j) n Sj : = pj ∧ tempj end for until(S = S. old) n output S

What’s the problem? n Image computation has two parts n n n Cross-over images are expensive! n n Transitions local to a partition (i=j) Transitions Crossing over partitions (i<>j) Get BDDs, maybe from disk Store BDDs, maybe over network Reorder large BDDs The classical algorithm does one set of cross -over image during each EX.

Outline Background The Partitioning Approach Model Checking n n n The naïve algorithm An improved algorithm Experiments and Conclusion

Least Fix Point E(p. Uq) n n S : = q, S. old : = NULL repeat S. old : = S n forall (partitions j) n repeat n Sj. old : = Sj n Sj : = Sj ∨ (pj ∧ EXl(Sj , j)) … under-approximate until(Sj = Sj. old) end for n S : = S ∨ (p ∧ EXc(S)) … add missing states n until(S = S. old) n output S

Greatest Fix Point EGp n n n S : = p Border : = p ∧ EXc(S) repeat … candidate set S. old : = S n forall (partitions j) n repeat n Sj. old : = Sj n Sj : = pj ∧ (EXl(Sj , j) ∨ Borderj) … over-approx n until(Sj == Sj. old) end for n Border : = p ∧ EXc(S) … prune states n until(S == S. old) n output S

Outline Background The Partitioning Approach Model Checking n n n The naïve algorithm An improved algorithm Experiments and Conclusion
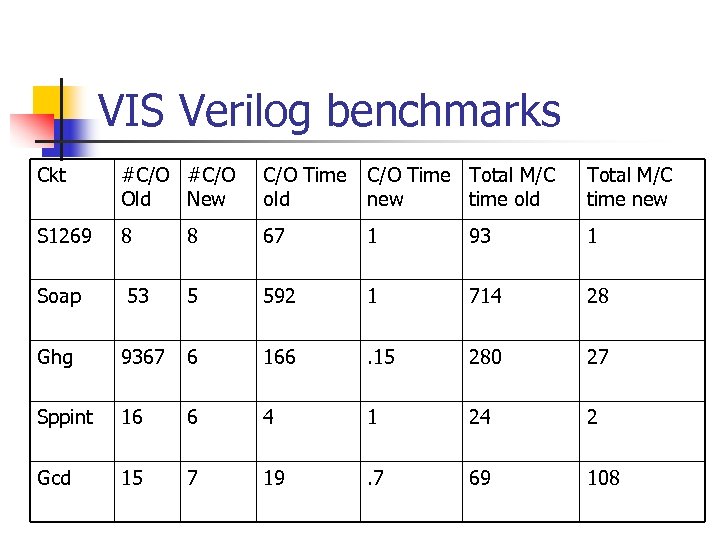
VIS Verilog benchmarks Ckt #C/O Old New C/O Time old C/O Time Total M/C new time old Total M/C time new S 1269 8 8 67 1 93 1 Soap 53 5 592 1 714 28 Ghg 9367 6 166 . 15 280 27 Sppint 16 6 4 1 24 2 Gcd 15 7 19 . 7 69 108

Conclusions Assuming a model where cross-over images are very expensive, the proposed algorithm: n n Is no worse than the classical algorithm Converges faster, empirically, in terms of n n n Reduces total model checking time n n Number of cross-over images Time spent in cross-over images Often quite significantly Is good for parallel model checking
6f8ce30f580a7791d0dd5dd5eb5e4ac6.ppt