c12befc0bb6fe477a9d49c818613ccc5.ppt
- Количество слайдов: 43

On Generalized Authorization Problems Stefan Schwoon University of Stuttgart Somesh Jha and Thomas Reps University of Wisconsin Stuart Stubblebine Research Labs

Weighted Pushdown Systems and their Application to Query Evaluation in SPKI/SDSI
![SPKI/SDSI Principals (Public Keys) KBob , KAlice Individuals K CS Department CS KOwner[R ] SPKI/SDSI Principals (Public Keys) KBob , KAlice Individuals K CS Department CS KOwner[R ]](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-3.jpg)
SPKI/SDSI Principals (Public Keys) KBob , KAlice Individuals K CS Department CS KOwner[R ] Owner of resource R Local Names KCS faculty KBob my. Students Extended Names KBob my. Students Spouse

Name Certs Bob is a CS faculty member KCS faculty KBob Alice is name cert also has a Each a student of Bob’s KBob my. Students KAlice validity specification (usually a time interval) Alice’s friends. . . KAlice my. Friends KJoe KAlice my. Friends KMary enemies spouse
![Auth Certs A CS faculty member can use host H KOwner[H ] KCS faculty Auth Certs A CS faculty member can use host H KOwner[H ] KCS faculty](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-5.jpg)
Auth Certs A CS faculty member can use host H KOwner[H ] KCS faculty Can delegate Bob allows access to his students auth my. Students KEach KBobcert also has Bob • a validity specification (time interval) Cannot • an authorization specification (e. g. , H ) delegate Alice allows access to her friends KAlice my. Friends
![KOwner[H ] Certificate Chain KOwner[H ] KCS faculty KBob KAlice my. Friends KBob my. KOwner[H ] Certificate Chain KOwner[H ] KCS faculty KBob KAlice my. Friends KBob my.](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-6.jpg)
KOwner[H ] Certificate Chain KOwner[H ] KCS faculty KBob KAlice my. Friends KBob my. Students Does not KBob my. Studentsapply! KBob my. Students KAlice

Pushdown System (PDS) States: { σ 1, σ 2 , σ 3 , σ 4 } Stack symbols: { A, B, C, D } Transition rules: <σ1, A> <σ2, e> <σ1, A> <σ2, B C>

Pushdown System (PDS) States: { σ1, σ2, σ3, σ4 }the If state is σ1 and the top Stack symbols: of the stack is. A, then { A, B, C, D } pop A transition to stateσ2 Transition rules: <σ1, A> <σ2, e> <σ1, A> <σ2, B C>

Pushdown System (PDS) States: { σ 1, σ 2 , σ 3 , σ 4 } If the state is σ1 and the top Stack symbols: of the stack is. A, then { A, B, C, D } pop A transition to stateσ2 Transition rules: push B <σ1, A> <σ2, e> <σ1, A> <σ2, B C>

Pushdown System (PDS) States: { σ 1, σ 2 , σ 3 , σ 4 } Stack symbols: the state is σ1 and the If { A, B, C, D } top of the stack is. A, then pop A Transition rules: transition to stateσ2 <σ1, A> <σ2, e> push C; then push B <σ1, A> <σ2, B> <σ1, A> <σ2, B C>
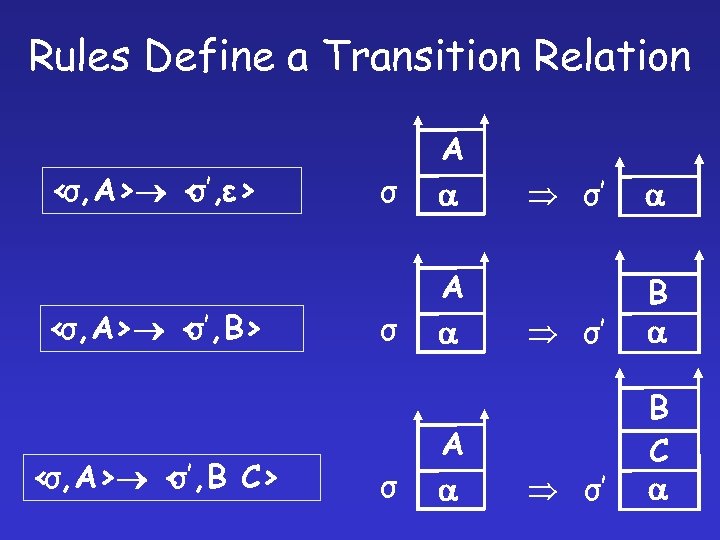
Rules Define a Transition Relation < σ, A> < σ’, ε> < σ, A> < σ’, B C> σ A σ’ σ’ B C

Pushdown System (PDS) • PDS = Pushdown automaton without <σ, A> an input tape • Mechanism for defining a class of <σ, AA> infinite-state transition systems <σ, A> <σ, A A> <σ, AAAA> ׃

PDS Terminology Configuration <σ, B A C> σ, B A C c c’ (transition relation) c’ follows from c by a transition rule c predecessor of c’ c’ successor of c c 0 c 1 . . cn (a run). c * c’ reflexive transitive closure of

PDS Terminology Configuration < Bob , my. Students K > KBob , my. Students c c’ (transition relation) c’ follows from c by a transition rule c predecessor of c’ c’ successor of c c 0 c 1 . . cn (a run). c * c’ reflexive transitive closure of
![A Certificate Chain is a Run < Owner[H ], > K < Owner[H ], A Certificate Chain is a Run < Owner[H ], > K < Owner[H ],](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-15.jpg)
A Certificate Chain is a Run < Owner[H ], > K < Owner[H ], > < CS, faculty > K K <KCS, faculty > <KCS, faculty> < Bob , >e K < Bob , > K < Bob , K > < Bob , my. Students K < Bob , my. Students K > e < Bob , my. Students > < Alice , > K K < Alice , K > >
![Basic Authorization Query: <KOwner[H ], > Pre*({<KAlice, □>, <KAlice, ■>})? < Owner[H ], > Basic Authorization Query: <KOwner[H ], > Pre*({<KAlice, □>, <KAlice, ■>})? < Owner[H ], >](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-16.jpg)
Basic Authorization Query: <KOwner[H ], > Pre*({<KAlice, □>, <KAlice, ■>})? < Owner[H ], > K S = {< Alice , >, K KAlice , >} < Pre*(S)

Representation Issue – <σ, A> <σ, e > – pre* ( {<σ, A>}) = { σ Ai | i ≥ 1 } . . . • The set of configurations pre*(S) can be infinite • Example <σ, AAA> <σ, A> • Solution in the PDS literature: <σ, e > Represent a set of configurations with an automaton
) pre*(M M ׃ ׃
![{<KAlice, >, <KAlice, >} KOwner[H ] KCS KBob { , KAlice } {<KAlice, >, <KAlice, >} KOwner[H ] KCS KBob { , KAlice }](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-19.jpg)
{<KAlice, >, <KAlice, >} KOwner[H ] KCS KBob { , KAlice }
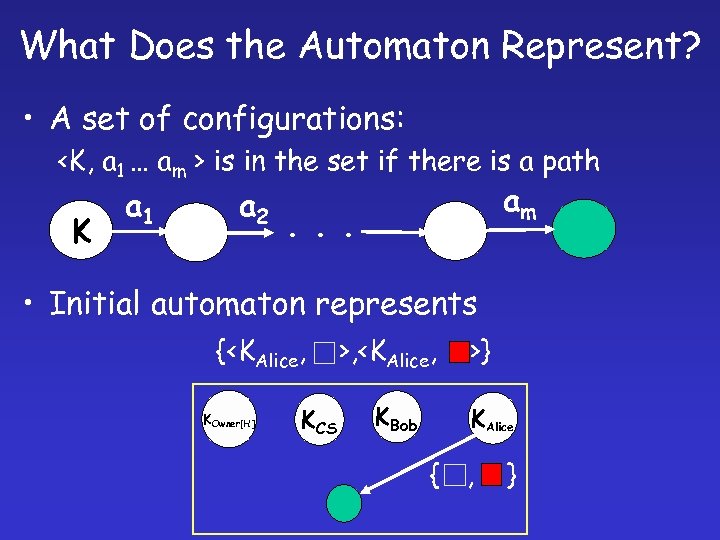
What Does the Automaton Represent? • A set of configurations: <K, a 1 … am > is in the set if there is a path K a 1 a 2 am . . . • Initial automaton represents {<KAlice, KOwner[H ] KCS >, <KAlice, KBob >} KAlice { , }
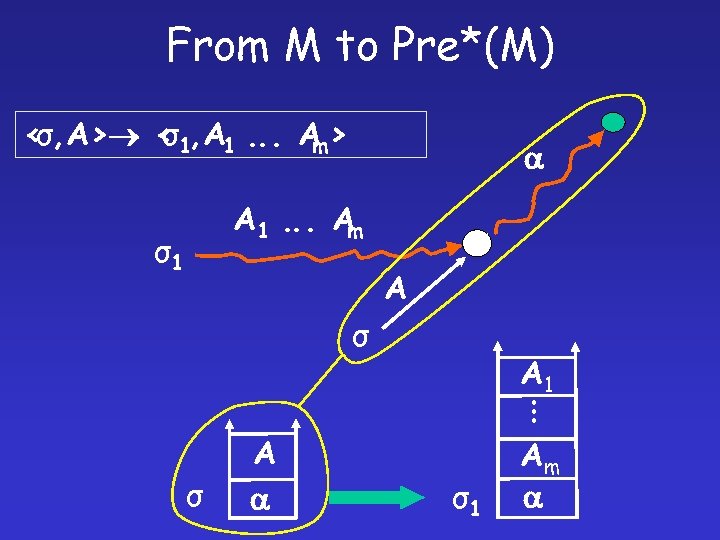
From M to Pre*(M) < σ, A> < 1, A 1. . . A > σ m A 1. . . A m σ1 A σ . . . A 1 σ A σ1 Am
![Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , < Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , <](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-22.jpg)
Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , < Bob , my. Students > < Alice , e> K K < CS, faculty > < Bob , e> K K KAlice }
![Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , < Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , <](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-23.jpg)
Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , < Bob , > < Bob , my. Students ■> K K < Owner[H ], > <K , faculty > K CS KAlice }
![Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , KAlice Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , KAlice](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-24.jpg)
Pre*({<KAlice, >, <KAlice, >}) my. Students faculty KOwner[H ] KCS KBob { , KAlice } <KOwner[H ], > Pre*({<KAlice, □>, <KAlice, ■>})

Time and Space Complexity • n. K : number of principals • |C|: sum of the lengths of the right-hand sides of the certs in C • Pre* – Time complexity: O(n 2 |C|) K – Space complexity: O(n. K |C|) • Post* 2 – Time and space complexity: O(n. K |C| + nk |C|2)

SPKI/SDSI Query Evaluation Application Pushdown Systems Weighted Pushdown Systems

Weighted Pushdown System (WPDS) States: { σ 1, σ 2 , σ 3 , σ 4 } Stack symbols: { A, B, C, D } Transition rules: w 1 <σ1, A> <σ2, e> w 2 <σ1, A> <σ2, B> w 3 <σ1, A> <σ2, B C>

Privacy using a Weighted PDS <KInsurer, □> <KH, patient ■> <KH, patient> <KAIDS, patient> <KH, patient> <KIM, patient> <KAIDS, patient> <KAlice, e> <KIM, patient> <KAlice, e> S I I S I
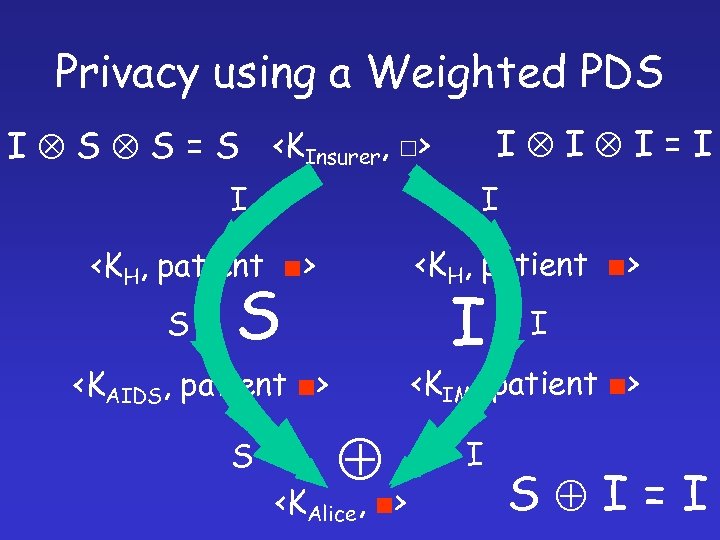
Privacy using a Weighted PDS I I I=I I S S = S <KInsurer, □> I I <KH, patient ■> S S I <KIM, patient ■> <KAIDS, patient ■> S I <KAlice, ■> I S I=I

Idempotent Semiring (D, , , 0, 1) [= Meet Semilattice (D, , . . . )] a 0=a a b=b a a (b c) = (a b) c a a=a a b iff a b = a = a 1=a a (b c) = (a b) c a (b c) = (a b) (a c) (a b) c = (a c) (b c) a 0=0 a=a
![“Auth Cert Reduction is Incomplete” Li & Mitchell [CSFW 03] Rule Authorization KOwner[D] KAlice “Auth Cert Reduction is Incomplete” Li & Mitchell [CSFW 03] Rule Authorization KOwner[D] KAlice](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-31.jpg)
“Auth Cert Reduction is Incomplete” Li & Mitchell [CSFW 03] Rule Authorization KOwner[D] KAlice {read} KOwner[D] KAlice {write} Request Does KAlice have {read, write} access to D? No RFC 2693: “Remove all certificates whose authorization is not {read, write}”
![Authorization using a Weighted PDS <KOwner[D], > {read} Cert chain? ! {write} = <KAlice, Authorization using a Weighted PDS <KOwner[D], > {read} Cert chain? ! {write} = <KAlice,](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-32.jpg)
Authorization using a Weighted PDS <KOwner[D], > {read} Cert chain? ! {write} = <KAlice, ■> {read} {write} = {read, write}
![Authorization using a Weighted PDS <KOwner[D], > {read} Cert tree {write} = <KAlice, ■> Authorization using a Weighted PDS <KOwner[D], > {read} Cert tree {write} = <KAlice, ■>](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-33.jpg)
Authorization using a Weighted PDS <KOwner[D], > {read} Cert tree {write} = <KAlice, ■> {read} {write} = {read, write}
![Validity using a Weighted PDS Rule KOwner[D] KAlice Validity 10 20 Request Does KAlice Validity using a Weighted PDS Rule KOwner[D] KAlice Validity 10 20 Request Does KAlice](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-34.jpg)
Validity using a Weighted PDS Rule KOwner[D] KAlice Validity 10 20 Request Does KAlice have the right to access D? If so, what is the cert chain with the largest validity value?
![Validity using a Weighted PDS <KOwner[D], > 10 20 = max <KAlice, ■> max(10, Validity using a Weighted PDS <KOwner[D], > 10 20 = max <KAlice, ■> max(10,](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-35.jpg)
Validity using a Weighted PDS <KOwner[D], > 10 20 = max <KAlice, ■> max(10, 20) = 20
![Authorization + Validity Rule Authorization KOwner[D] KAlice {read} KOwner[D] KAlice {write} Authorization Validity 10 Authorization + Validity Rule Authorization KOwner[D] KAlice {read} KOwner[D] KAlice {write} Authorization Validity 10](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-36.jpg)
Authorization + Validity Rule Authorization KOwner[D] KAlice {read} KOwner[D] KAlice {write} Authorization Validity 10 20 0 1 {rlidwka} max min - {read, write}, 20 ? {read: 10, write: 20}
![Authorization + Validity <KOwner[D], > {read: 10} {write: 20} <KAlice, ■> {read: 10} {write: Authorization + Validity <KOwner[D], > {read: 10} {write: 20} <KAlice, ■> {read: 10} {write:](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-37.jpg)
Authorization + Validity <KOwner[D], > {read: 10} {write: 20} <KAlice, ■> {read: 10} {write: 20} = {read: 10, write: 20}
![Authorization + Validity <KOwner[D], > {r: 10, w: 15, l: 10} {r: 5, w: Authorization + Validity <KOwner[D], > {r: 10, w: 15, l: 10} {r: 5, w:](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-38.jpg)
Authorization + Validity <KOwner[D], > {r: 10, w: 15, l: 10} {r: 5, w: 20, k: 5} <KAlice, ■> {r: 10, w: 15, l: 10} {r: 5, w: 20, k: 5} = {r: 10, w: 20, l: 10, k: 5}
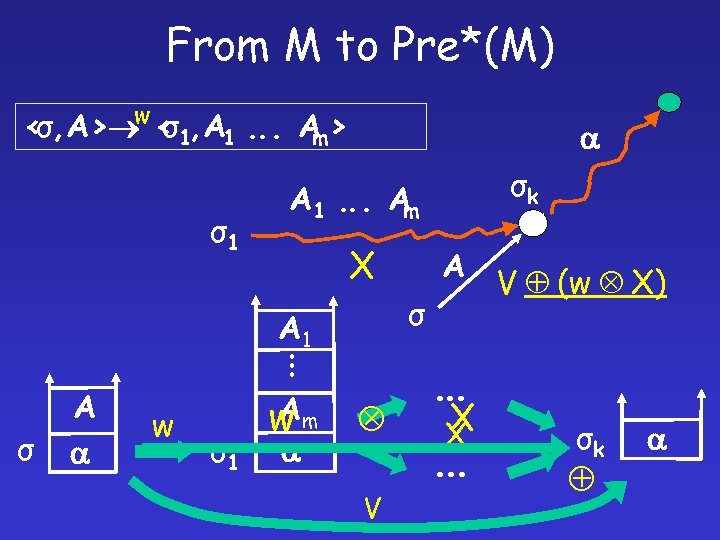
From M to Pre*(M) w < σ, A> < 1, A 1. . . A > σ m σ1 A 1. . . A m X. . . σ w σ1 A σ A 1 A σk A wm V V (w X) . . . X X . . . σk

Contributions • SPKI/SDSI anomalies solved via weighted PDSs – Authorization – Validity – Certificate chains • Not just basic authorization queries – Jha & Reps [CSFW 02] • SPKI/SDSI semantics – infinite-state transition system – meet-over-all-paths values • Construction of certificate trees • Threshold certs (slight extension) • Publicly available implementation (WPDS Library) – Supports both post* and pre* queries

Other Applications of WPDSs • Reps, T. , Schwoon, S. , and Jha, S. , Weighted pushdown systems and their application to interprocedural dataflow analysis. In Proc. of the Static Analysis Symposium, 2003. • Supports a broader set of dataflow-analysis queries than past work (30 years worth. . . )
![Related Work • SPKI/SDSI – [see paper] • Pushdown systems – Bouajjani, Esparza, & Related Work • SPKI/SDSI – [see paper] • Pushdown systems – Bouajjani, Esparza, &](https://present5.com/presentation/c12befc0bb6fe477a9d49c818613ccc5/image-42.jpg)
Related Work • SPKI/SDSI – [see paper] • Pushdown systems – Bouajjani, Esparza, & Maler [Concur 97] – Esparza et al. [CAV 00] – Bouajjani, Esparza, & Touili [POPL 03] • Weighted-hypergraph problems – – Knuth [IPL 77] Grammar flow analysis: Möncke & Wilhelm [WAGA 91] Ramalingam thesis [LNCS #1089] Ramalingam & Reps [J. Alg 96] • Dataflow analysis – Sharir & Pnueli 81 – IDE framework: Sagiv, Reps, & Horwitz [TCS 96]

c12befc0bb6fe477a9d49c818613ccc5.ppt