On Discovering Moving Clusters in Spatio-temporal Data Panos

On Discovering Moving Clusters in Spatio-temporal Data Panos Kalnis National University of Singapore Nikos Mamoulis University of Hong Kong Spiridon Bakiras Hong Kong University of Science and Technology

What is a Moving Cluster? Dense clusters of objects that move similarly for a long time period p Not necessarily the same objects during the lifetime of the cluster p Examples p n n n p Migrating animals Convoy of cars Military applications Solutions: n Efficient exact and approximate algorithms

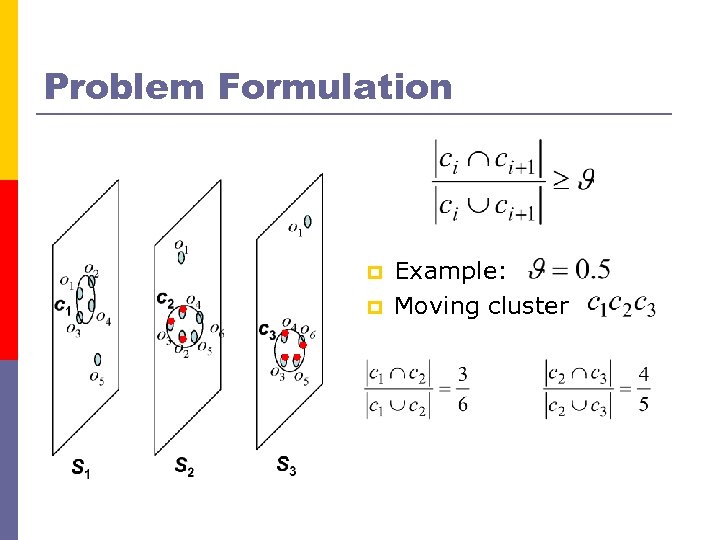Problem Formulation p p Example: Moving cluster

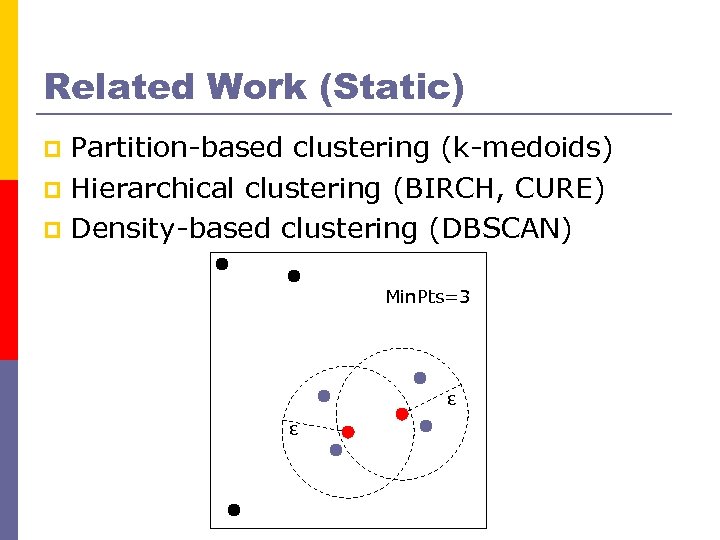Related Work (Static) Partition-based clustering (k-medoids) p Hierarchical clustering (BIRCH, CURE) p Density-based clustering (DBSCAN) p Min. Pts=3 ε ε

Related Work (Moving Objects) p Grouping trajectories n n p n [Hadjieleftheriou et. al, SSTD 03] Static dense regions No common objects between regions in sequence Incremental DBSCAN/OPTICS n p Trajectory cluster: Constant set of objects through its lifetime Only similar movement; no space proximity Dense areas over time n p [Vlachos et. al, ICDE 02] Only a small percentage of objects moves Maintaining Data Bubbles n [Ester et. al, VLDB 98] [Nassar et. al, SIGMOD 04] Redistributes updated objects in existing bubbles

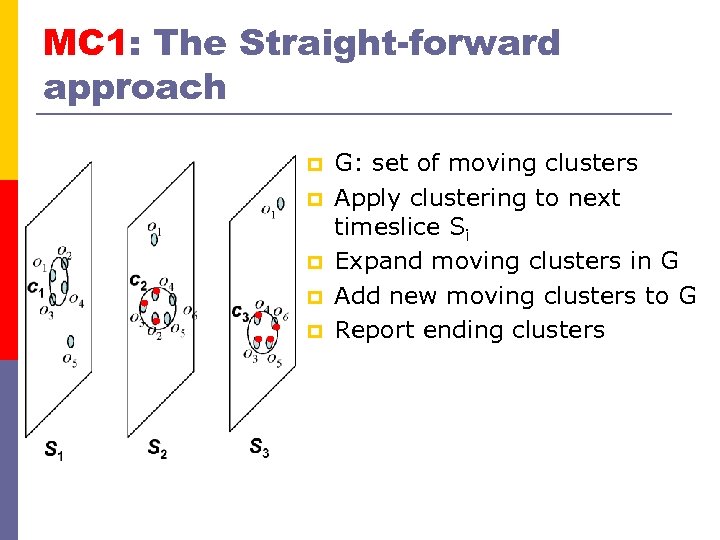MC 1: The Straight-forward approach p p p G: set of moving clusters Apply clustering to next timeslice Si Expand moving clusters in G Add new moving clusters to G Report ending clusters

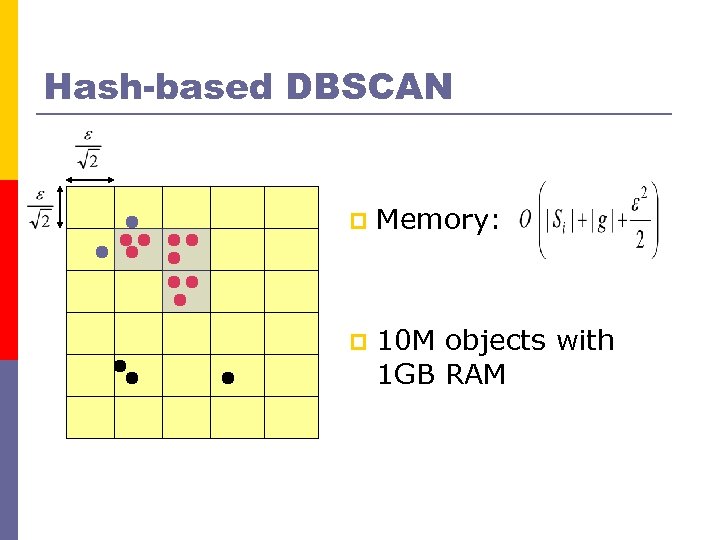Hash-based DBSCAN p Memory: p 10 M objects with 1 GB RAM

MC 1 is inefficient! 1. 2. Checks all possible combination of clusters in consecutive timeslices Performs clustering for every timeslice

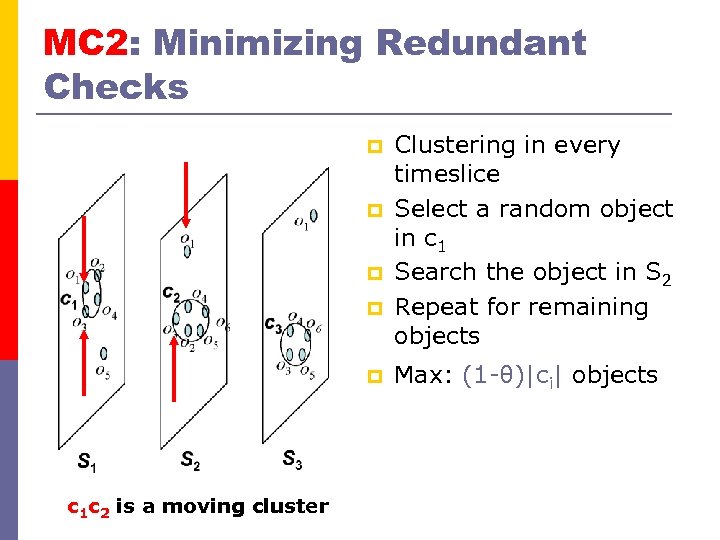MC 2: Minimizing Redundant Checks p p p c 1 c 2 is a moving cluster Clustering in every timeslice Select a random object in c 1 Search the object in S 2 Repeat for remaining objects Max: (1 -θ)|ci| objects

Ambiguity Cases: θ<0. 5 {c 0 c 1, c 2} {c 0 c 2, c 1}

MC 3: Approximate Moving Clusters Intuition: Many clusters will remain the same even if objects move p Avoid performing clustering in every timeslice p For an object o p n n If o belongs to cluster c in timeslice Si Assume that o also belongs to c in the next timeslice (notice: objects may have moved)

Refine clusters Hash new clusters in a grid p Legal cluster: p n n Does not meet/intersect with other clusters It is connected (cells meet) Objects in legal clusters are not considered further p For the rest of the objects, perform clustering p Possible inaccuracies!!! p

Minimize Error Perform exact clustering to absorb (may not eliminate) the accumulated error p Period for exact clustering: Grows linearly, drops exponentially p Exact clustering: If more that α|G| clusters have been added/removed p

Experimental Evaluation p p 10 K-50 K objects per timeslice 50 -100 timeslices, up to 5 M objects Linux, C++, 1. 3 GHz CPU, 1. 2 GB RAM Generator: Clusters move/rotate, objects appear/disappear

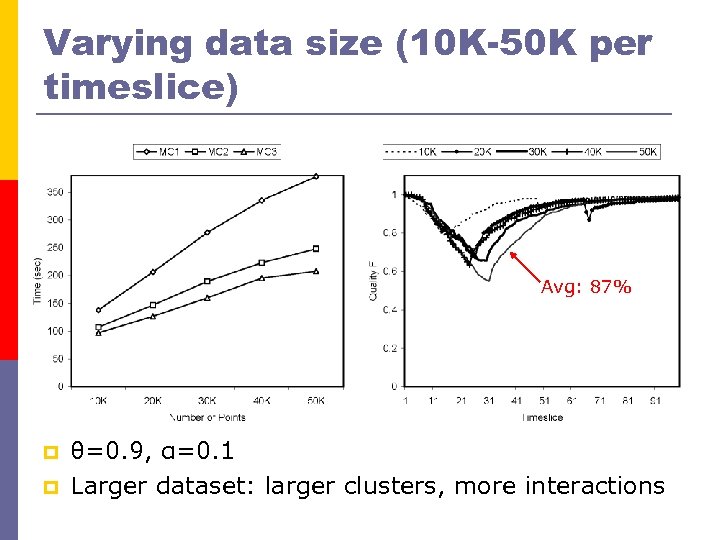Varying data size (10 K-50 K per timeslice) Avg: 87% p p θ=0. 9, α=0. 1 Larger dataset: larger clusters, more interactions

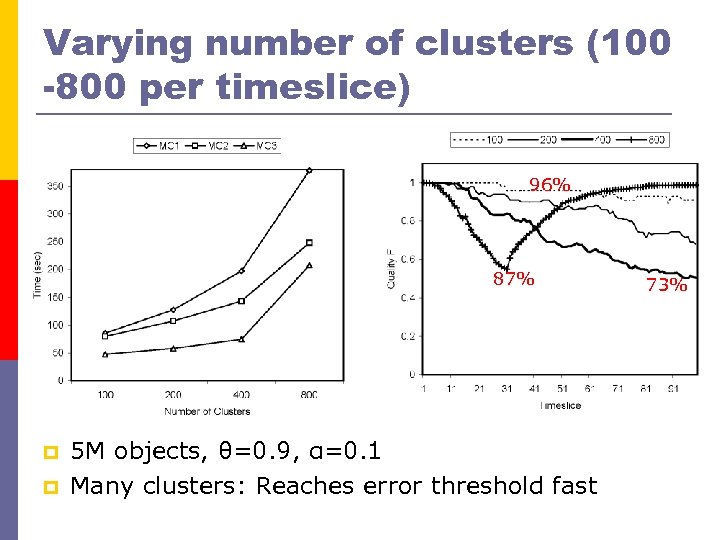Varying number of clusters (100 -800 per timeslice) 96% 87% p p 5 M objects, θ=0. 9, α=0. 1 Many clusters: Reaches error threshold fast 73%

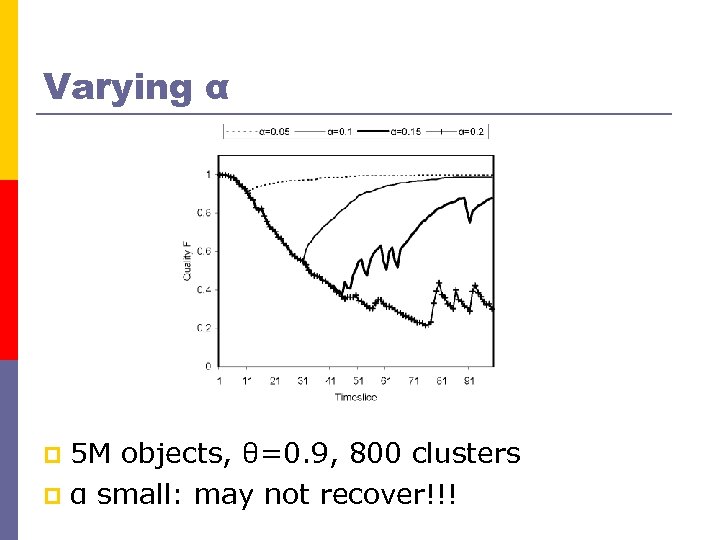Varying α 5 M objects, θ=0. 9, 800 clusters p α small: may not recover!!! p

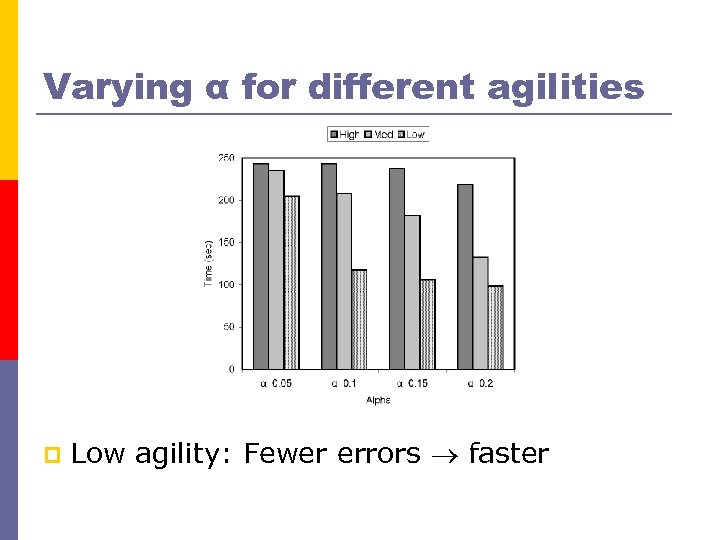Varying α for different agilities p Low agility: Fewer errors faster

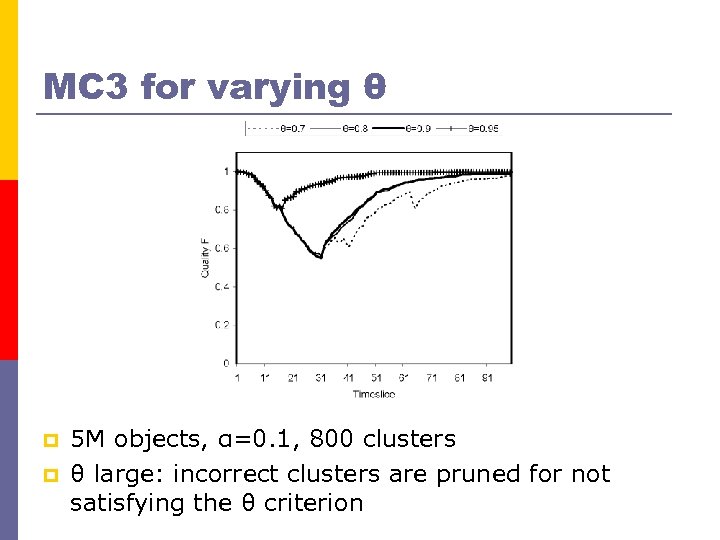MC 3 for varying θ p p 5 M objects, α=0. 1, 800 clusters θ large: incorrect clusters are pruned for not satisfying the θ criterion

Conclusions p Moving clusters n n p Objects may move/change Exact and approximate solutions Future work n n n Automatic setting of parameter α Better error estimation Constraints (e. g, moving cluster must span at least k timeslices)

Questions?