 Окружность P М N A О А C D
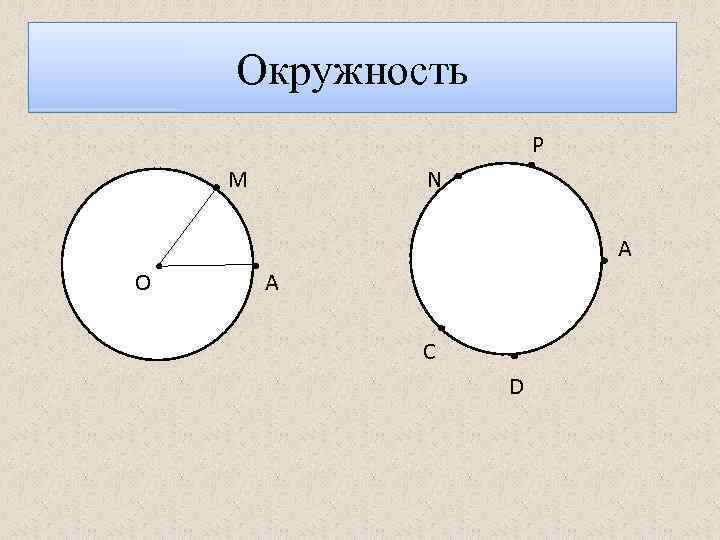
Окружность P М N A О А C D
 Деление на части 1)на 2 части 2)на 4 части С 3)на 8 частей С R В А AА В А K В A M D 4)на 12 частей С O D 5)на 6 частей Z P O Z F B A G B A T E H D N E H Указать длины дуг: 2)AD 3)AR, KM, ND, AM, NA 4)AO, AG, CB, CE, AT, AE, PE 5)AZ, ZB, AB, ZH, OZ
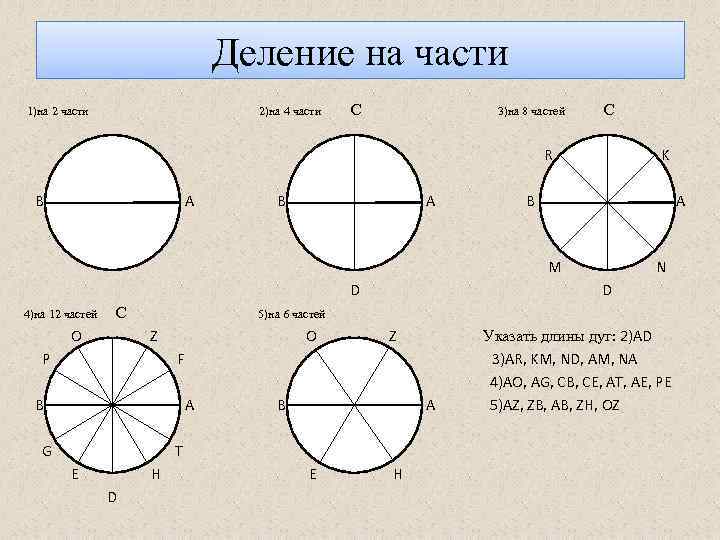
Деление на части 1)на 2 части 2)на 4 части С 3)на 8 частей С R В А AА В А K В A M D 4)на 12 частей С O D 5)на 6 частей Z P O Z F B A G B A T E H D N E H Указать длины дуг: 2)AD 3)AR, KM, ND, AM, NA 4)AO, AG, CB, CE, AT, AE, PE 5)AZ, ZB, AB, ZH, OZ
 Отметить на числовой окружности точки М( t) такие, что: 1)t = 1; 4; - 3 2)t = π; π/3; -π/6; 7π 3)t = - 0, 5π; 2, 5π; - 0, 75π 4)t = 2π/3; - 5π/6; 7π/4; 5)t = - 11π/3; 25π/6; 19π/4 1 рад≈57° π≈3, 14 π(рад)=180° 1 π 0
Отметить на числовой окружности точки М( t) такие, что: 1)t = 1; 4; - 3 2)t = π; π/3; -π/6; 7π 3)t = - 0, 5π; 2, 5π; - 0, 75π 4)t = 2π/3; - 5π/6; 7π/4; 5)t = - 11π/3; 25π/6; 19π/4 1 рад≈57° π≈3, 14 π(рад)=180° 1 π 0
 Числовая окружность в системе координат. 2 ч (-; +) у π/2 у. М π 1 ч (+; +) 1 α х. М М(t)=M(x; y) ум 0 х 2π 3π/2 3 ч (-; -) 4 ч (+; -) х = cosα = cost y = sinα = sint у/х = tgt x/y = ctgt м M
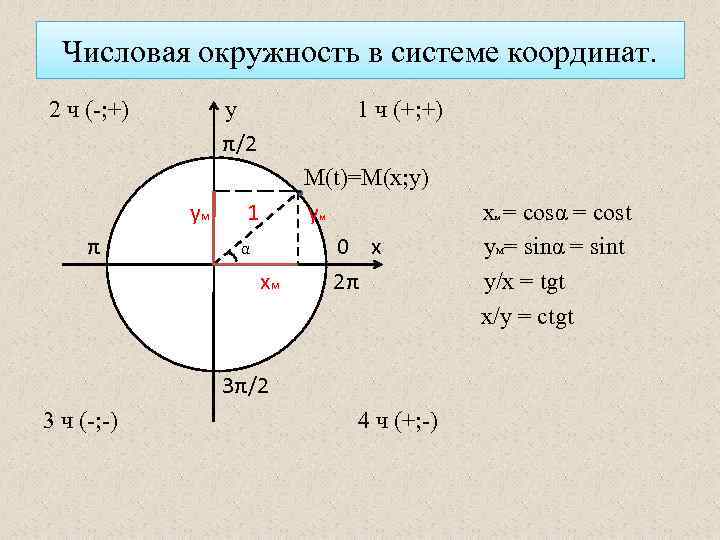
Числовая окружность в системе координат. 2 ч (-; +) у π/2 у. М π 1 ч (+; +) 1 α х. М М(t)=M(x; y) ум 0 х 2π 3π/2 3 ч (-; -) 4 ч (+; -) х = cosα = cost y = sinα = sint у/х = tgt x/y = ctgt м M
 Координаты у π/2 90° 120° 2π/3 135° 3π/4 1 150° 5π/6 1/2 - π/6 30° 0 180° π -1 - π/3 60° π/4 45° 1 0 0° ½ -1/2 210° 7π/6 225° 5π/4 240° 4π/3 -1/2 -1 270° 3π/2 [-π/2] (sint) 2π 360 x (cost) 11π/6 330° [-π/6] 7π/4 315° [-π/4] 5π/3 300° [-π/3]
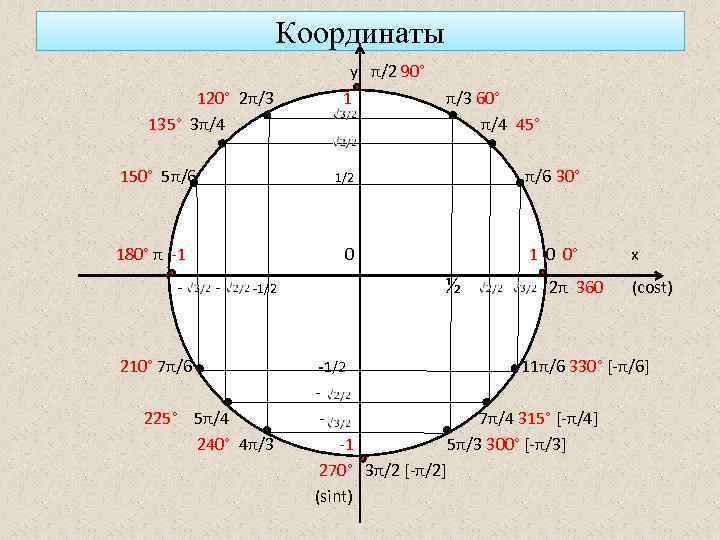
Координаты у π/2 90° 120° 2π/3 135° 3π/4 1 150° 5π/6 1/2 - π/6 30° 0 180° π -1 - π/3 60° π/4 45° 1 0 0° ½ -1/2 210° 7π/6 225° 5π/4 240° 4π/3 -1/2 -1 270° 3π/2 [-π/2] (sint) 2π 360 x (cost) 11π/6 330° [-π/6] 7π/4 315° [-π/4] 5π/3 300° [-π/3]
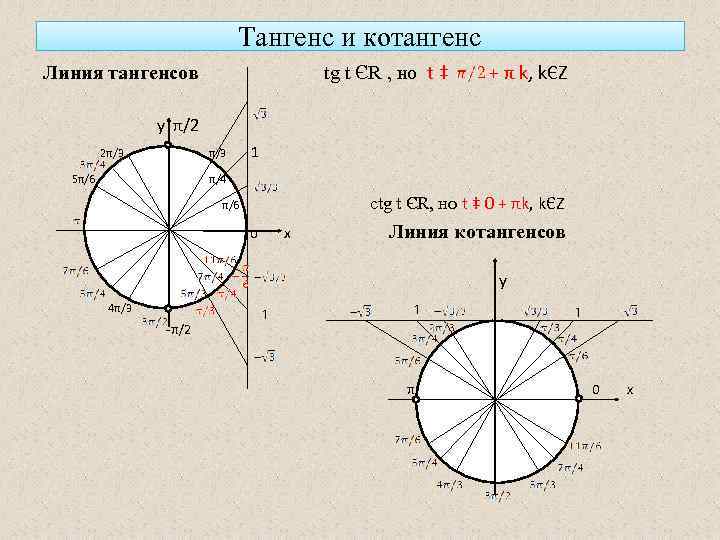 Тангенс и котангенс tg t ЄR , но t ‡ Линия тангенсов + π k, kЄZ у π/2 2π/3 5π/6 1 π/4 ctg t ЄR, но t ‡ 0 + πk, kЄZ π/6 0 х Линия котангенсов у 4π/3 -π/2 π 0 х
Тангенс и котангенс tg t ЄR , но t ‡ Линия тангенсов + π k, kЄZ у π/2 2π/3 5π/6 1 π/4 ctg t ЄR, но t ‡ 0 + πk, kЄZ π/6 0 х Линия котангенсов у 4π/3 -π/2 π 0 х
 Знаки и значения 1. sint > 0 в 1 ч и 2 ч; 2. cost > 0 в 1 ч и 4 ч; sint < 0 в 3 ч и 4 ч; cost < 0 в 2 ч и 3 ч; sint Є [-1; 1] cost Є [-1; 1] 1)sin²t + cos²t=1 2) y ² + x² = 1 3. tgt > 0 в 1 ч и 3 ч; 4. сtgt > 0 в 1 ч и 3 ч; tgt < 0 в 2 ч и 4 ч; сtgt < 0 в 2 ч и 4 ч; tgt Є R ctgt Є R 3)tgt = sint/cost ; ctgt = cost/sint 4)tgt = y/x ; ctgt = x/y 5)tgt·ctgt = 1
Знаки и значения 1. sint > 0 в 1 ч и 2 ч; 2. cost > 0 в 1 ч и 4 ч; sint < 0 в 3 ч и 4 ч; cost < 0 в 2 ч и 3 ч; sint Є [-1; 1] cost Є [-1; 1] 1)sin²t + cos²t=1 2) y ² + x² = 1 3. tgt > 0 в 1 ч и 3 ч; 4. сtgt > 0 в 1 ч и 3 ч; tgt < 0 в 2 ч и 4 ч; сtgt < 0 в 2 ч и 4 ч; tgt Є R ctgt Є R 3)tgt = sint/cost ; ctgt = cost/sint 4)tgt = y/x ; ctgt = x/y 5)tgt·ctgt = 1
 Самостоятельная работа № 1 1 вариант 2 вариант 1. На числовой окружности отметить числа: 9π/4; 2; -8π A -5π/3; 3; 6π 2. Единичная окружность разбита на части: K E 13π/6; - 1; 10π F 3 вариант A M D K C S G D C R H B E P D O T C N R H B Найдите длины следующих дуг: CA, CS, CG, BD 1) cos 95° 2) sin 7π/3 3) tg (-π/6) CE, CR, CH, HR 3. Определить знак числа: 1) cos 280° 2) sin 11π/6 3) tg (-π/4) CT, CP, CN, RD 1) cos 190° 2) sin 13π/4 3) tg (-π/3)
Самостоятельная работа № 1 1 вариант 2 вариант 1. На числовой окружности отметить числа: 9π/4; 2; -8π A -5π/3; 3; 6π 2. Единичная окружность разбита на части: K E 13π/6; - 1; 10π F 3 вариант A M D K C S G D C R H B E P D O T C N R H B Найдите длины следующих дуг: CA, CS, CG, BD 1) cos 95° 2) sin 7π/3 3) tg (-π/6) CE, CR, CH, HR 3. Определить знак числа: 1) cos 280° 2) sin 11π/6 3) tg (-π/4) CT, CP, CN, RD 1) cos 190° 2) sin 13π/4 3) tg (-π/3)
 Работа с формулами № 1. Дано: cost=0, 4; 90°0 sint=+ sint = Ответ: . 2 способ. А 5 2 С cos = 2/5 ; СВ= Т. К. tЄ2 ч, то sin t>0. Значит, sin t= В Ответ: .
Работа с формулами № 1. Дано: cost=0, 4; 90°0 sint=+ sint = Ответ: . 2 способ. А 5 2 С cos = 2/5 ; СВ= Т. К. tЄ2 ч, то sin t>0. Значит, sin t= В Ответ: .
 Основные тригонометрические тождества 1.
Основные тригонометрические тождества 1.
 Формулы приведения y π/2+t π/2 -t 1). Определить четверть π–t 2π+t π 0 x π+t 2π-t 3π/2+t 2). Определить знак функции в четверти 3). От ОХ – не меняем на ко функцию; От ОУ – меняем на ко функцию.
Формулы приведения y π/2+t π/2 -t 1). Определить четверть π–t 2π+t π 0 x π+t 2π-t 3π/2+t 2). Определить знак функции в четверти 3). От ОХ – не меняем на ко функцию; От ОУ – меняем на ко функцию.
 Формулы сложения 1. sin(x + y)= sinx·cosy + siny·cosx 2. cos(x + y)= cosx·cosy - sinx·siny 3. sin(x – y)= sinx·cosy - siny·cosx 4. cos(x – y)= cosx·cosy + sinx·siny 5. 6.
Формулы сложения 1. sin(x + y)= sinx·cosy + siny·cosx 2. cos(x + y)= cosx·cosy - sinx·siny 3. sin(x – y)= sinx·cosy - siny·cosx 4. cos(x – y)= cosx·cosy + sinx·siny 5. 6.
 Формулы двойного и половинного аргумента 1. sin 2 x = 2 sinx·cosx; 2. cos 2 x = cos²x - sin²x; 3. cos 2 x = 1 – 2 sin²x; 6. 4. cos 2 x = 2 cos²x-1; 7. 5. ;
Формулы двойного и половинного аргумента 1. sin 2 x = 2 sinx·cosx; 2. cos 2 x = cos²x - sin²x; 3. cos 2 x = 1 – 2 sin²x; 6. 4. cos 2 x = 2 cos²x-1; 7. 5. ;
 Преобразование сумм тригонометрических функций в произведение 1. 2. 3. 4. 5. - вспомогательный угол
Преобразование сумм тригонометрических функций в произведение 1. 2. 3. 4. 5. - вспомогательный угол