Оценка сложности алгоритмов Основы теории сложности P NP

Оценка сложности алгоритмов. Основы теории сложности (P, NP)

время выполнения программы ► ввод (порядок ввода) исходной информации в программу; ► качество скомпилированного кода исполняемой программы; ► машинные инструкции (естественные и ускоряющие) ► временная сложность алгоритма. Т(n) = cn 2 Тср(n)

Теория алгоритмов — наука, изучающая общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления ► Классическая теория алгоритмов ► Теория асимптотического анализа алгоритмов ► Теория практического анализа вычислительных алгоритмов

Асимптотические соотношения ► Для описания скорости роста функций используется О-нотация ► Время выполнения Т(n) некоторой программы имеет порядок О(n 2) (читается «о-большое от n в квадрате» или «о от n в квадрате» ), то подразумевается, что существуют положительные константы с и n 0 такие, что для всех n, больших или равных n 0, выполняется неравенство Т(n) ≤ с n 2.

Асимптотический анализ алгоритмов ► Цель - сравнение затрат времени и других ресурсов различными алгоритмами, предназначенными для решения одной и той же задачи, при больших объемах входных данных. ► Оценка функции трудоёмкости - сложность алгоритма

► О - верхняя асимптотическая оценка трудоемкости алгоритма ► как быстро растет трудоемкость алгоритма с увеличением объема данных

► Определение. Функция Т(n) имеет порядок О(f(n)), если существуют константы с и n 0 такие, что для всех n ≥ n 0 выполняется неравенство Т(n) ≤ cf(n). Для программ, у которых время выполнения имеет порядок О(f(n)), говорят, что они имеют порядок (или степень) роста f(n).

► Т ( n) = 3 n 3 + 2 n 2 О(n 3) правило сумм: трудоемкость выполнения конечной последовательности программных фрагментов, без учета констант, имеет порядок фрагмента с наибольшим временем выполнения.

Пример ► О(n 2), О(n 3) и О(nlogn) ► O(max(n 2, n 3)) - О(n 3) ► O(max(n 3, nlogn)) - О(n 3)

► правило произведений: если Т 1(n) и Т 2(n) имеют степени роста O(f(n)) и O(g(n)) соответственно, то произведение Т 1(n)Т 2(n) имеет степень роста O(f(n)g(n)). Например O(cf(n)) == O(f(n)), с – положительная константа. О(n 2 / 2) == О(n 2).

Пример: Алгоритм вычисления значения многочлена степени n в заданной точке x Pn(x) = anxn + an-1 xn-1 +. . . + aixi +. . . + a 1 x 1 + a 0 Алгоритм - для i-го слагаемого(i=1. . n) требует I умножений. 1 + 2 + 3 +. . . + n = n(n+1)/2 умножений. n+1 сложений. Всего: n(n+1)/2 + n + 1= n 2/2 + 3 n/2 + 1 операций

► f(n) = n 2/2 + 3 n/2 + 1 -> n 2/2 ► O(n 2) верхняя оценка (исключительно асимптотику!) количество операций (а значит, и время работы) растет не быстрее, чем квадрат количества элементов

► при малых n O(n 2) быстрее n 2 + 10 n + 6 O(n) 1000000 n + 5

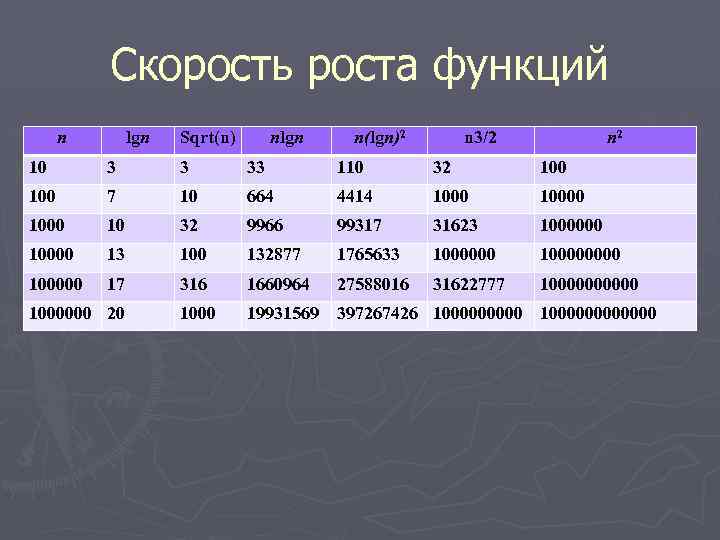Скорость роста функций n lgn Sqrt(n) nlgn n(lgn)2 n 3/2 n 2 10 3 3 33 110 32 100 7 10 664 4414 10000 1000 10 32 9966 99317 31623 1000000 13 100 132877 1765633 100000000 100000 17 316 1660964 27588016 31622777 100000 1000 19931569 397267426 1000000000000 1000000 20

► Для нижней асимптотической оценки роста функции T(n) используется Ω (омега). T(n) = Ω (nlogn) обозначает класс функций, которые растут не медленнее, чем f(n) nlogn

► Для задания одновременно верхней и нижней оценки роста функции T(n) используется Θ (тэтта). ► Равенство T(n) = Θ(f(n)) выполняется тогда и только тогда, когда T(n)=O(f(n)) и T(n) = Ω (f(n)).

Асимптотические оценки можно представить в порядке увеличения скорости их роста: O(1) < O(log 2 n) < O(nlog 2 n) < O(n 2) < O(n 3) < O(2 n).

f(n) = Ω(n 2) даже в самом удачном случае будет произведено не менее n 2 действий f(n) = O(n 2) гарантирует, что в самом худшем случае действий будет порядка n 2, не больше. Θ(n 2) всегда будет выполняться порядка n 2 операций. Существует только тогда, когда O() и Ω() совпадают и равна им.

Итого O() асимптотическая оценка алгоритма на худших входных данных Ω() на лучших входных данных Θ() сокращенная запись одинаковых O() и Ω().

Классы сложности ► P-сложные, ► NP-сложные, ► экспоненциально сложные ► и др

Класс P ► задачи, которые могут быть решены за время, полиномиально зависящее от объёма исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга) время работы не слишком сильно зависит от размера входных данных

Примеры алгоритмов класса P ► целочисленного сложения, ► умножения, ► деления, ► взятия остатка от деления, ► перемножения матриц (n 3 умножений) ► выяснение связности графов ► простое число (O(n 12) операций, n — длина записи числа ) ► и другие.

P - ? ? ? , но не доказано обратно 1. 2. 3. 4. 5. Задача коммивояжёра. (остальные NP-полные задачи) Разложение на множители составного числа. Дискретное логарифмирование числа a по простому модулю p (a

Класс NP (non-deterministic polynomial) задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины (то есть машины, следующее состояние которой не всегда однозначно определяется предыдущими) время работы сильно зависит от размера входных данных свидетелей решения - ? ?

► Всякую задачу, принадлежащую NP, можно решить за экспоненциальное время (перебором всех возможных свидетелей длины меньше nc).

Примеры задач класса NP P-? ? ? ► Задача выполнимости булевых формул. ► Задача о клике. ► Проблема существования гамильтонова цикла в графе. ► Задача о коммивояжёре. ► Существование целочисленного решения системы линейных неравенств.

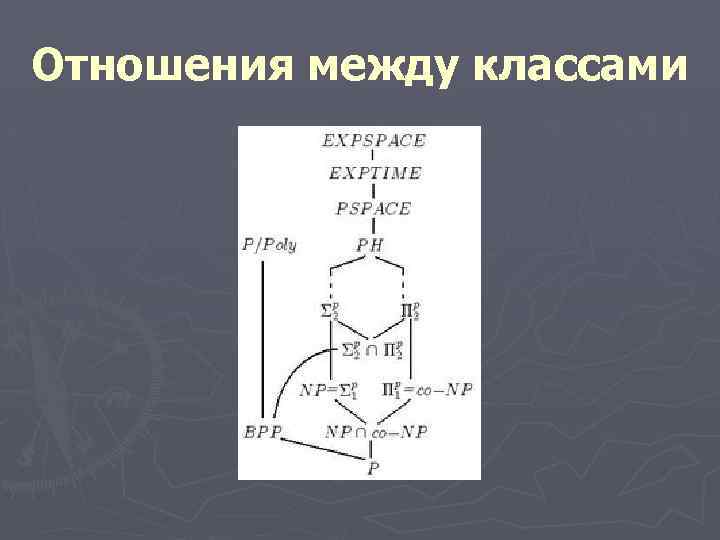Отношения между классами

МЕДИАНЫ и ПОРЯДКОВЫЕ СТАТИСТИКИ ► i-ая порядковая статистика ► максимум - порядковая статистика n ► минимум - порядковая статистика 1 ► медиана - i=(n+1)/2 i=n/2+1 меньшая из двух