Оценка сложности алгоритмов Часть 2 На первой

Оценка сложности алгоритмов Часть 2

На первой парте В классе учатся n учеников. Учитель хочет выбрать двоих учеников для первой парты. Сколькими способами это можно сделать? n n-1

На первой парте В классе учатся n учеников. Учитель хочет выбрать двоих учеников для первой парты. Сколькими способами это можно сделать? Учитель хочет выбрать учеников так, чтобы разница между их средними баллами была минимальной. Написать программу, которая позволит определить номера подходящих учеников.

На первой парте min_r: =32000; nom 1: =-1; nom 2: =-1; for i: =1 to n do for j: =1 to n do if (i<>j) and (abs(a[i]-a[j])) then begin nom 1: =i; nom 2: =j; min_r: = abs(a[i]-a[j]); end; 2 O(n )

Отрезки Из n точек подсчитать количество всевозможных троек, из которых можно построить невырожденный треугольник. 3) O(n

Сложные алгоритмы procedure Slow; var i, j, k: integer; begin for i: =1 to N do for j: =1 to N do for k: =1 to N do {какое-то действие} end; procedure Fast; var i, j: integer; begin for i: =1 to N do for j: =1 to N do Slow; end; procedure Both; begin Fast; end; O(N^2)*O(N^3)=O(N^5)

Сложные алгоритмы procedure Slow; var i, j, k: integer; begin for i: =1 to N do for j: =1 to N do for k: =1 to N do {какое-то действие} end; procedure Fast; var i, j: integer; begin for i: =1 to N do for j: =1 to N do {какое-то действие} end; procedure Both; begin Fast; Slow; end; O(N^2)+O(N^3)=O(N^3)

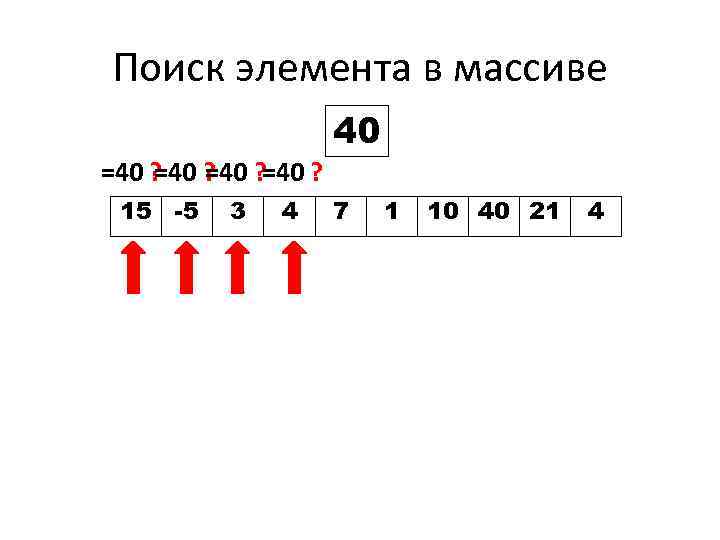Поиск элемента в массиве 40 =40 ? ? 40 ? =40 = 15 -5 3 4 7 1 10 40 21 4

Поиск элемента в массиве. Линейный поиск for i: =1 to n do readln(a[i]); ind: =-1; for i: =1 to n do begin if a[i]=v then ind: =I; break; end; writeln(ind); O(n) – при неудачном поиске O(n/2) – при удачном поиске

Поиск элемента в массиве. Бинарный поиск nom: =-1; while (r>=l) do begin 2 m: =(l+r)/2; if a[m]=v then begin nom: =m; break; end else if (v<=a[m]) then r: =m-1 else l: =m+1; end; O(log n)

Общие функции оценки сложности 1. C – константа 2. log(N)) 3. log(N) 4. N^C, 01 8. C^N, C>1 9. N!

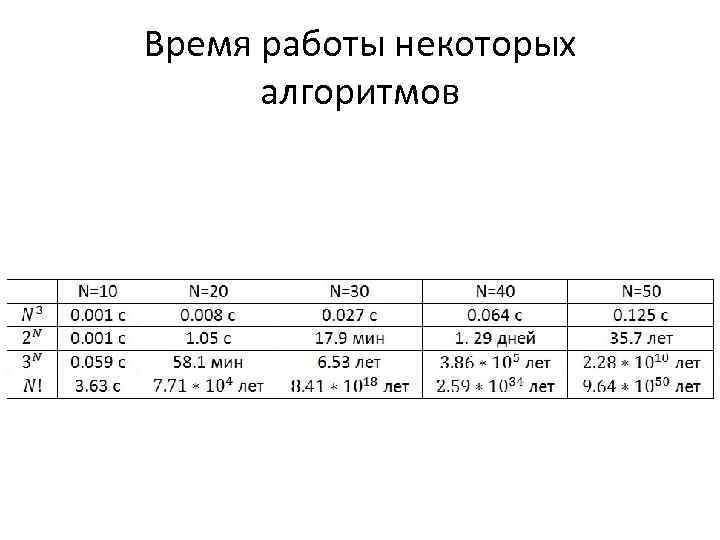Время работы некоторых алгоритмов