OC Traders 02 28 09 Orange County Investools Users Group

OC Traders 02/28/09 Orange County Investools Users Group Rowena St. Moritz

Volatility after the Options Industry Council’s Workshop on Volatility Rowena St. Moritz

Volatility Reflects Price Changes n Volatility reflects fluctuations in the price n Not necessarily an uptrend n Not necessarily a downtrend n Greater fluctuations = greater volatility 02/28/09 Rowena St. Moritz 3

Volatility Two Types of Volatility 1. Historical Volatility 2. Implied Volatility 02/28/09 Rowena St. Moritz 4

Historical Volatility Rowena St. Moritz

Historical Volatility n Past volatility, usually annual n An observed fact, not a prediction n Is no guarantee of future volatility n Usually based on daily closing prices 02/28/09 Rowena St. Moritz 6

Historical Volatility n Annualized Standard Deviation (SD) of daily price changes, expressed in percent n The percent amount is relative change, up or down, from the average price n Stocks, options, indexes and sectors have historical volatility 02/28/09 Rowena St. Moritz 7

Historical Volatility n Annualized Standard Deviation (SD) of daily price changes, expressed in percent n Prices within 1 SD ~ 68% of the time n Prices within 2 SDs ~ 95% of the time n Prices within 3 SDs ~ 99% of the time 02/28/09 Rowena St. Moritz 8

Historical Volatility Illustration n If a stock has an average closing price of $100 and 25% historical volatility, then statistically ~ 68% of the time (1 SD) Price was within + or - $25 ($75 to $125) ~ 95% of the time (2 SDs) Price was within + or - $50 ($50 to $150) ~ 99% of the time (3 SDs) Price was within + or - $75 ($25 to $175) 02/28/09 Rowena St. Moritz 9

Historical Volatility n Available at http: //www. optionseducation. org/quotes/ n Enter the equity symbol n Click on “Historical Volatility” 02/28/09 Rowena St. Moritz 10

Historical Volatility Example n Example for IWM on 2/22/09 http: //www. optionseducation. org/quotes/ 02/28/09 Rowena St. Moritz 11

Historical Volatility Indexes, Sectors, Stocks, and Options have it n Some sectors may have lower or higher volatility levels, but… n Volatility often changes, even when spread across sectors or indexes n Volatility of stocks within sectors may vary 02/28/09 Rowena St. Moritz 12

Implied Volatility Rowena St. Moritz

Implied Volatility n Implied volatility is what people often mean when they just say “volatility” n It is expected volatility, a guess n It is a subjective prediction n It is an assumption about a stock’s volatility up to the option’s expiration 02/28/09 Rowena St. Moritz 14

Implied Volatility n By definition, it implies a stock’s future volatility, but… n Implied volatility is a feature only of options 02/28/09 Rowena St. Moritz 15

Implied Volatility Only Options Have It n Stocks do not have implied volatility Stocks have historic volatility only n Options do have implied volatility Calls have implied volatility n Puts have implied volatility n 02/28/09 Rowena St. Moritz 16

Implied Volatility n Can be at great variance with historical volatility n Is not necessarily right or wrong n May change abruptly and significantly n An option’s implied volatility can change without a change in the underlying stock’s price 02/28/09 Rowena St. Moritz 17

Implied Volatility n Predicts a range of future possible stock prices n Higher volatility = greater range of possible stock prices n Lower volatility = smaller range of possible stock prices 02/28/09 Rowena St. Moritz 18

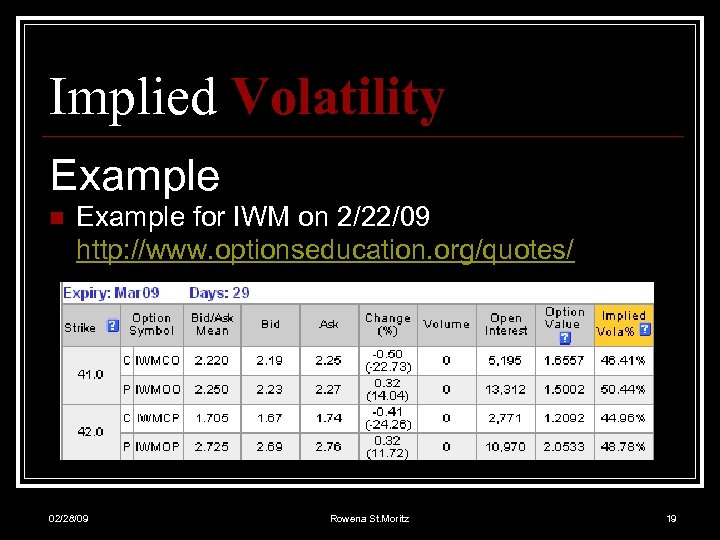Implied Volatility Example n Example for IWM on 2/22/09 http: //www. optionseducation. org/quotes/ 02/28/09 Rowena St. Moritz 19

Implied Volatility n Index Options’ Implied Volatility Symbols n S&P 500 30 -day implied volatility VIX is what people usually mean by “the” volatility index n Dow Jones Industrial Avg 30 -day implied volatility VXD n Nasdaq 100 30 -day implied volatility VXN n Russell 2000 30 -day implied volatility RVX 02/28/09 Rowena St. Moritz 20

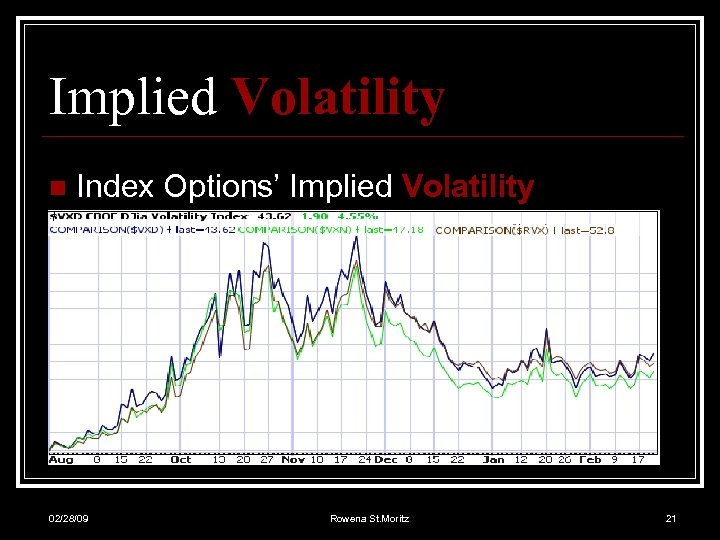Implied Volatility n Index Options’ Implied Volatility 02/28/09 Rowena St. Moritz 21

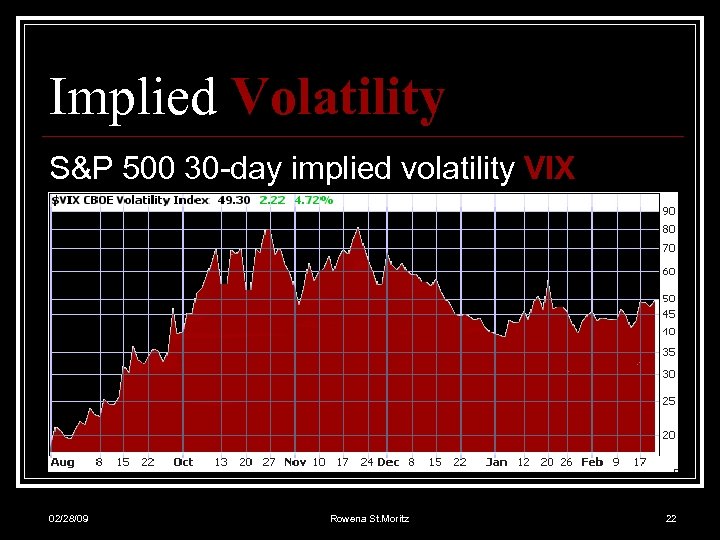Implied Volatility S&P 500 30 -day implied volatility VIX 02/28/09 Rowena St. Moritz 22

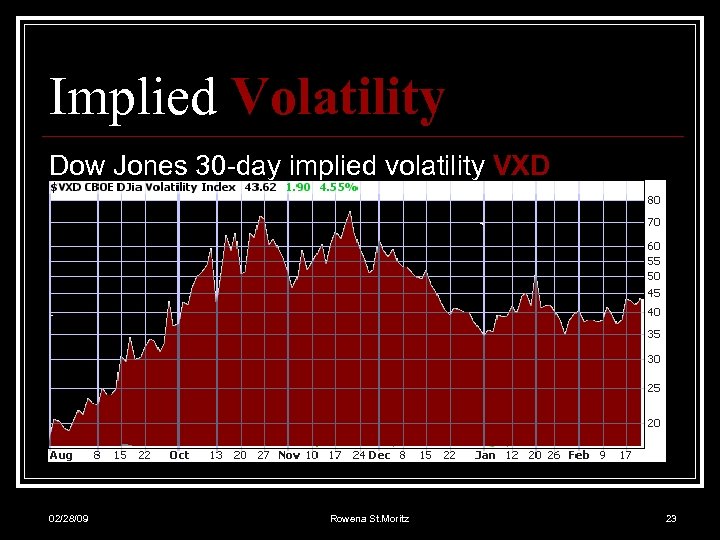Implied Volatility Dow Jones 30 -day implied volatility VXD 02/28/09 Rowena St. Moritz 23

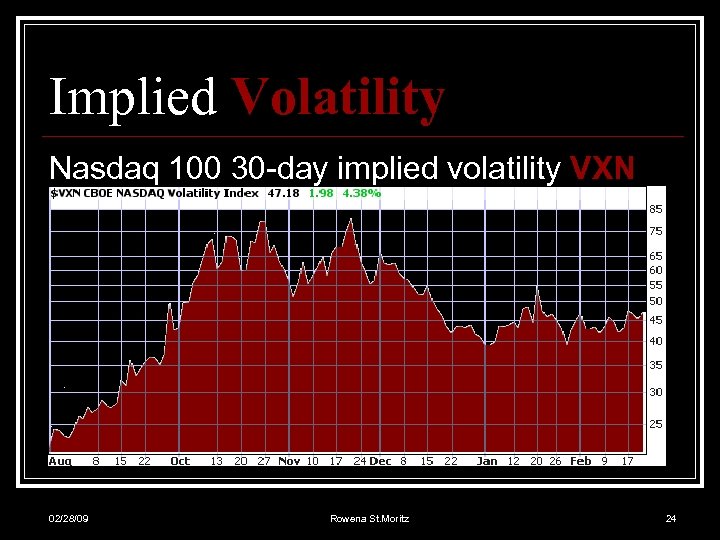Implied Volatility Nasdaq 100 30 -day implied volatility VXN 02/28/09 Rowena St. Moritz 24

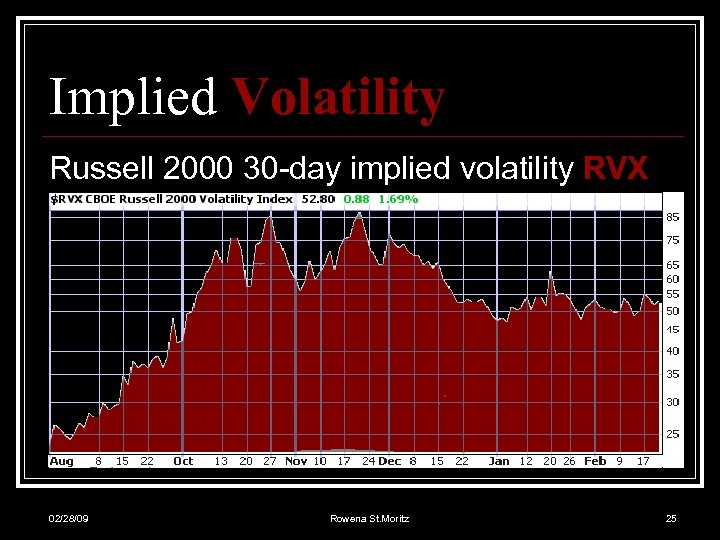Implied Volatility Russell 2000 30 -day implied volatility RVX 02/28/09 Rowena St. Moritz 25

Implied Volatility Things that affect implied volatility n n General stock market psychology Economic data, Federal Reserve actions, and other news Change in the implied volatility of other option classes within the same industry sector Market activity (volume) 02/28/09 Rowena St. Moritz 26

Implied Volatility Things that increase implied volatility Rising volume n Drop in price n Bad news n Nearing an announcement (e. g. earnings) n 02/28/09 Rowena St. Moritz 27

Implied Volatility Things that decrease implied volatility Declining volume n Rise in price n Good news n After an announcement (e. g. earnings) n 02/28/09 Rowena St. Moritz 28

Price and Implied Volatility Rowena St. Moritz

Price and Implied Volatility An Option’s price has two components 1. Intrinsic value 2. Time value 02/28/09 Rowena St. Moritz 30

Price and Implied Volatility Option’s Time Value n Time until expiration (known) n Cost of money (known or predictable) n Interest n Dividends n Volatility (unpredictable) n As the cost of money approaches zero, volatility is a greater portion of time value 02/28/09 Rowena St. Moritz 31

Price and Implied Volatility n Implied Volatility = Risk n Implied Volatility affects option premium n Higher volatility means higher option premium n Lower volatility means lower option premium 02/28/09 Rowena St. Moritz 32

Price and Implied Volatility n Higher volatility n Sellers want more for their increased risk n Buyers pay more n Lower volatility n Sellers take less for their decreased risk n Buyers pay less 02/28/09 Rowena St. Moritz 33

Price and Implied Volatility n As stock volatility increases, the price of calls and puts generally increases n As stock volatility decreases, the price of calls and puts generally decreases 02/28/09 Rowena St. Moritz 34

Price and Implied Volatility n If you are long a call or a put, then you want the option’s implied volatility to increase so that the option’s price will go up n If you are short a call or a put, then you want the option’s implied volatility to decrease so that the option’s price will go down 02/28/09 Rowena St. Moritz 35

Price and Implied Volatility’s Effect on Options n Greatest nominal (dollar) effect on ATM Calls and Puts (because they have the greatest time value) n Greatest percentage effect on OTM Calls and Puts n Least effect on ITM Calls and Puts because they have so little time value 02/28/09 Rowena St. Moritz 36

Vega and Implied Volatility Rowena St. Moritz

Vega and Implied Volatility Vega is “one of the Greeks” n Vega is theoretical - in reality, price changes may differ from those predicted by Vega n Vega’s value decreases with time n Stock has zero Vega 02/28/09 Rowena St. Moritz 38

Vega and Implied Volatility n Vega is expressed in dollars/cents n Shows expected option price change for a 1%-point change in implied volatility n Can be expressed per option or per contract n Spreads and other complex positions have a net vega (positive for long positions and negative for short positions) 02/28/09 Rowena St. Moritz 39

Vega and Implied Volatility Illustration of Implied Volatility’s relationship to Vega n $80 Call is $3. 50 ($350 per contract) n Implied Volatility is 35% and Vega is $. 15 n If underlying equity’s price remains unchanged n If Implied Volatility rises 1 point, the contract price is expected to rise $15 to $365 n If Implied Volatility falls 1 point, the contract price is expected to fall $15 to $335 02/28/09 Rowena St. Moritz 40

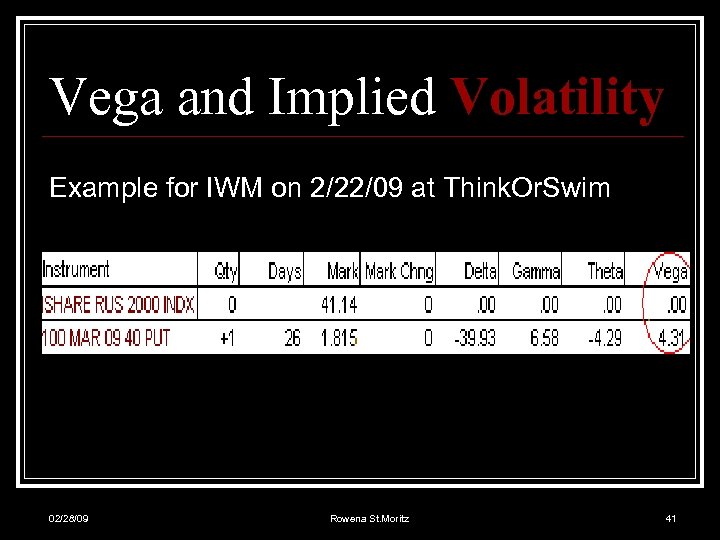Vega and Implied Volatility Example for IWM on 2/22/09 at Think. Or. Swim 02/28/09 Rowena St. Moritz 41

Vega and Implied Volatility Explanation of Example for IWM on 2/22/09 at To. S n $40 IWM March Put is $1. 815 n Implied Volatility is 52. 35% n Vega is 4. 31 per contract or $. 0431 for the option n If IWM’s price is unchanged and Implied Volatility n Rises 1 pt, contract price is expected to rise to $185. 81 n Falls 1 pt, contract price is expected to fall to $177. 19 02/28/09 Rowena St. Moritz 42

Vega and Implied Volatility Vega’s Bell Curve n Vega is greatest on ATM Calls and ATM Puts (because they have the greatest time value) n Vega is smaller on OTM Calls and OTM Puts n Vega is smallest on ITM Calls and ITM Puts 02/28/09 Rowena St. Moritz 43

Conclusions Rowena St. Moritz

Conclusions Buy Low and Sell High n Refers to volatility as well as price n Sell options during high volatility n Buy options during low volatility 02/28/09 Rowena St. Moritz 45

Conclusions Buy Low Volatility and Sell High Volatility n If earnings are coming out and the stock’s volatility is up n n n You believe that the stock’s price will skyrocket after the earnings announcement You want to buy a Call to profit from the price increase Consider selling a Put, instead of buying a Call n You can buy back the Put right after volatility drops n Even if the stock’s price doesn’t rise, you may profit from decreased volatility – you can be wrong and still profit 02/28/09 Rowena St. Moritz 46

Conclusions Thinkorswim’s recommendations on volatility n When volatility is low and rising n n n Purchase Calendar Spreads Purchase Double Diagonal Spreads When volatility is high and falling n Sell Iron Condors n Sell Vertical Spreads 02/28/09 Rowena St. Moritz 47

The End Rowena St. Moritz