ОБЗОР МЕТОДА РЕЛАКСАЦИИ ДЛЯ ПОИСКА ТОЧЕК РАВНОВЕСИЯ ПО НЭШУ В НЕПРЕРЫВНЫХ НЕКООПЕРАТИВНЫХ ИГРАХ МНОГИХ ЛИЦ Студент: Чиркина Д. Н. , 5 курс Научный руководитель: д. т. н. , профессор, Карпенко А. П.
План презентации n Введение ¨ Общие сведение. История задачи. Применение. n Постановка ¨ Основные n Метод задачи понятия и определения. релаксации Нэша ¨ Основы метода, его алгоритм и классификация. n Результат работы алгоритма на типовом примере ¨ Программная реализация. Исследование работы. n Заключение ¨ Оценка 2/10 эффективности. Выводы.
Введение n n Дж. Ф. Нэш, «Точки равновесия в играх n лиц» (1950 г. ) Разнообразие методов поиска равновесия по Нэшу: ¨ ¨ ¨ n n n Метод Никайдо и Изода, Метод Розена, Метод Смейла, методы частично-целочисленного программирования и другие. Джасек Б. Краусцек, Университет Виктории (г. Веллингтон, Новая Зеландия), Станислав Ярясев, Университет Флориды (США), 1999 г. Алгоритм релаксации для поиска точек равновесия по Нэшу и его экономическое приложение. (2000 г. ) Области применения: Механизмы поиска оптимальных решений в системах поддержки принятия управленческих решений (СППР) ¨ Оптимизация для повышения быстродействия задачи конфликтнооптимального целераспределения малых групп летательных аппаратов. 3/10 ¨
Постановка задачи nn игроков взаимодействуют друг с другом n Xi – набор возможных альтернативных стратегий n – действие игрока i n Совокупность действий всех игроков n n Множество (возможных) коллективных действий или множество ситуаций n n Функция 4/10 платы (цены):
Постановка задачи n Задана игра n Решение – точка равновесия по Нэшу, если справедливо неравенство n n Сокращенная форма записи n Пусть n Решение – точка равновесия по Нэшу, если справедливо неравенство n 5/10
Метод релаксации Нэша , n n Вектор коллективных действий. n Оптимальная функция отклика (ответа): n Функция n Вектор Никайдо и Изода точек равновесия по Нэшу n Условие: 6/10
Метод релаксации Нэша n Алгоритм релаксации: ¨ 1) Инициализация: , ¨ 2) Вычисление вектора ¨ 3) 7/10 : Cтандартные условия окончания поиска
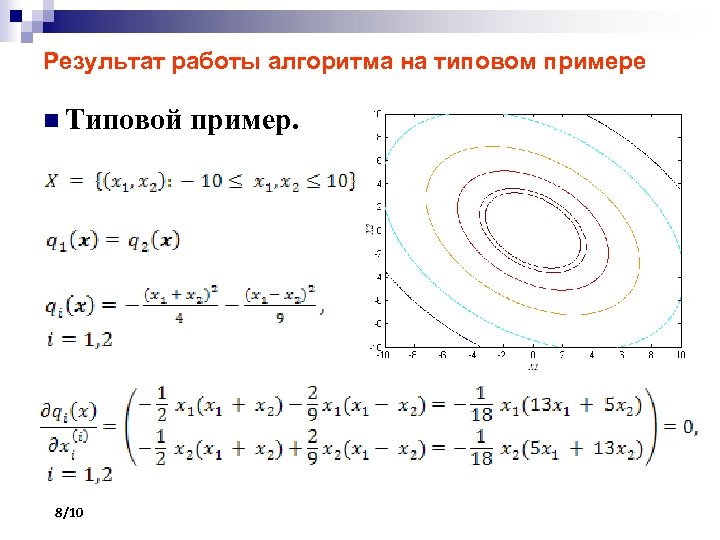
Результат работы алгоритма на типовом примере n Типовой 8/10 пример.
Результат работы алгоритма на типовом примере n Аналитические ¨ Ценовая функция: ¨ Функция ¨ Ценовая оптимального отклика функция ¨ Критерий 9/10 9 выражения окончания итераций
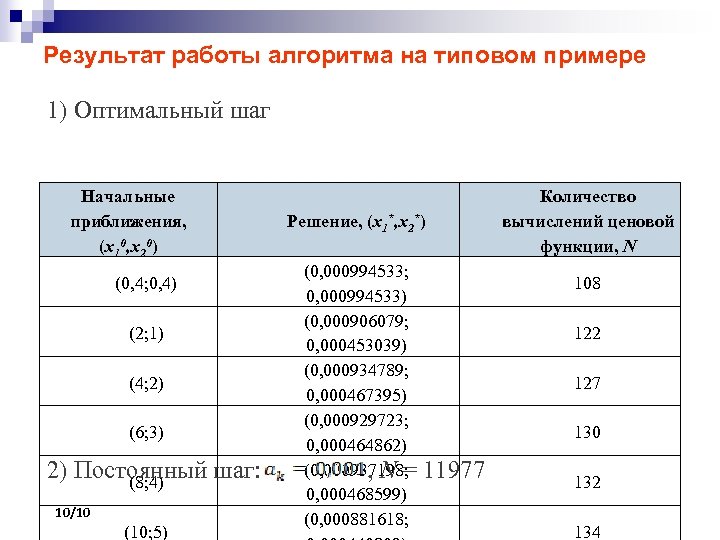
Результат работы алгоритма на типовом примере 1) Оптимальный шаг Начальные приближения, (x 10, x 20) (0, 4; 0, 4) (2; 1) (4; 2) (6; 3) 2) Постоянный шаг: (8; 4) 10/10 (10; 5) Решение, (x 1*, x 2*) (0, 000994533; 0, 000994533) (0, 000906079; 0, 000453039) (0, 000934789; 0, 000467395) (0, 000929723; 0, 000464862) (0, 000937198; , N= 0, 000468599) (0, 000881618; Количество вычислений ценовой функции, N 108 122 127 130 11977 132 134
Заключение n Преимущества: ¨ простота реализации алгоритма ¨ применимость для решения исследуемой задачи ¨ высокая скорость сходимости n Недостатки: ¨ невозможность использования параллельных вычислений ¨ необходимость иметь аналитические выражения для функций
БЛАГОДАРЮ ЗА ВНИМАНИЕ
Скачать презентацию ОБЗОР МЕТОДА РЕЛАКСАЦИИ ДЛЯ ПОИСКА ТОЧЕК РАВНОВЕСИЯ ПО
bd41a39a76abeb637cffc7d5cecbc1b4.ppt