Объём прямоугольного параллелепипеда Презентацию подготовили Шалаев Алексей Ученик 11 -а класса МАОУ СОШ № 25 и Уметбаева Кристина Ученица 11 -а класса МАОУ СОШ № 25 Учитель: Ремезова Валентина Николаевна Владимир, 2015 г
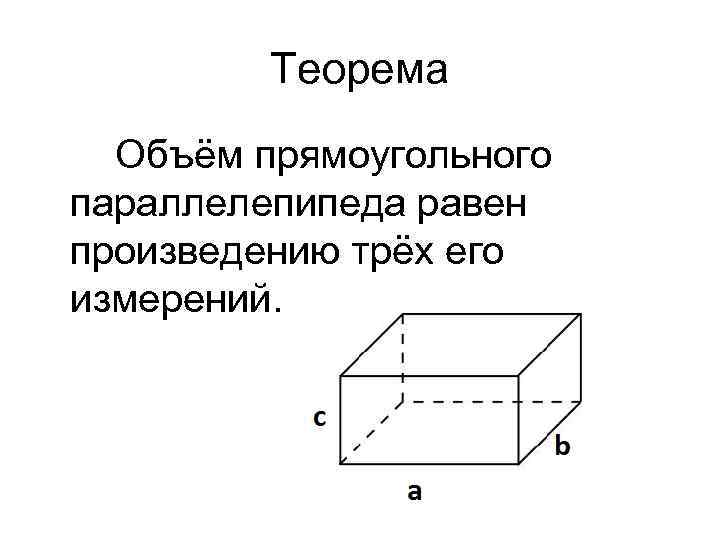
Теорема Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
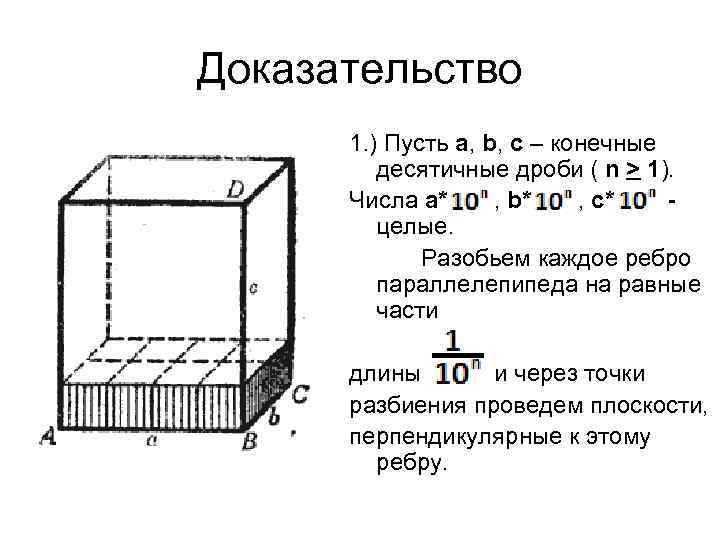
Доказательство 1. ) Пусть а, b, c – конечные десятичные дроби ( n > 1). Числа а* , b* , c* целые. Разобьем каждое ребро параллелепипеда на равные части длины и через точки разбиения проведем плоскости, перпендикулярные к этому ребру.
Параллелепипед разобьется на равных кубов с ребром . Т. к. объем каждого такого куба равен то объем всего параллелепипеда равен Итак, V . = abc. ,
2. ) Хотя бы одно из измерений a, b, c – бесконечная десятичная дробь. Пусть , – конечные десятичные дроби, полученные из чисел a, b, c отбрасыванием в каждом из них всех цифр после запятой, начиная с (n + 1). Тогда <a< , где (аналогично для b, c). Перемножим эти неравенства:
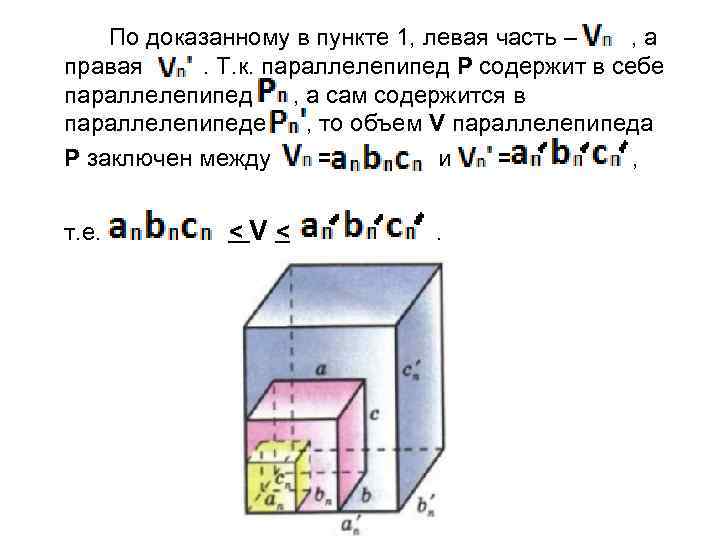
По доказанному в пункте 1, левая часть – , а правая. Т. к. параллелепипед Р содержит в себе параллелепипед , а сам содержится в параллелепипеде , то объем V параллелепипеда Р заключен между = и = , т. е. <V< .
При неограниченном увеличении n число будет становиться сколь угодно малым, и потому числа и будут сколь угодно мало отличаться друг от друга. Следовательно, число V сколь угодно мало отличается от числа abc. Значит они равны: V = abc.
Следствие 1. )Пусть измерения прямоугольного параллелепипеда, служащие сторонами его основания, выражаются числами а и b, а третье измерение (высота)—числом с. Тогда, обозначая объём его в соответствующих кубических единицах буквой V, можем написать: V = аbс Так как произведение а*b выражает площадь основания, то можнo сказать, что объём прямоугольного параллелепипеда равен произведению площади основания на высоту.
Спасибо за внимание!
Скачать презентацию Объём прямоугольного параллелепипеда подготовили Шалаев Алексей Ученик
Объём пр-ого пар-да.ppt