ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Решением, интегралом или интегральной кривой

Зарегистрируйтесь, чтобы просмотреть полный документ!

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Решением, интегралом или интегральной кривой ОДУ первого порядка или называется дифференцируемая функция y = y(x) , удовлетворяющая этому уравнению на некотором участке изменения аргумента x. Различают три типа задач: – задача Коши, когда для одного из значений аргумента, принимаемого за начальное, известно значение функции, т. е. y(x 0) = y 0; – граничная задача, когда условия на искомую функцию задаются для нескольких различных значений аргумента, y(x 0) = y 0; y(x 1) = y 1; y(x 2) = y 2; … – задачи на собственные значения, когда в формулировку задачи входят неопределенные параметры, определяемые из самой задачи. Численные методы следует применять только к корректно поставленным задачам, то есть таким для которых решение существует, единственно и непрерывно зависит от входных данных (от начальных, граничных условий и коэффициентов уравнения). Численное решение считается корректным, если исходная задача поставлена корректно и ее дискретный аналог сохраняет свойства корректности, т. е. полученная система алгебраических уравнений однозначно разрешима и устойчива по входным данным.

Задача Коши Требуется найти функцию y(x), удовлетворяющую дифференциальному уравнению где f(x, y(x)) – заданная непрерывная функцию двух аргументов. Теорема Пеано (условия существования и единственности решения задачи Коши) Пусть функция f(x, y(x)) непрерывна в открытой области D. Тогда через каждую точку (u, v) этой области проходит хотя бы одна интегральная кривая. Каждая интегральная кривая может быть продолжена в обе стороны вплоть до границы любой замкнутой области G, целиком содержащейся в D и содержащей точку (u, v) внутри себя. Кроме того, если функция f(x, y(x)) имеет в области D непрерывные частные производные первого порядка или удовлетворяет условию Липшица то задача Коши имеет единственное решение.

Устойчивость решения задачи Коши Рассмотри возмущенную задачу Коши где δ(x), γ – возмущения, вносимые в правую часть уравнения и начальные условия. Задача Коши абсолютно устойчива, если из условия следует , такое что Иначе, решение устойчиво, если малым возмущениям соответствуют малые изменения решения (имеет место непрерывная зависимость решения от входных данных) Рассмотрим устойчивость решения относительно возмущения начальных данных Оценим погрешность решения Для этого вычитая невозмущенное уравнение из возмущенного, получим

По теореме Лагранжа о среднем преобразуем правую часть Тогда решая полученное дифференциальное уравнение для погрешности Очевидно, что погрешность не будет возрастать, если Поскольку это требование должно выполняться для любого х, необходимо потребовать, чтобы выполнялось условие

Метод Пикара Проинтегрируем уравнение задачи Коши с помощью разделения переменных Используя последнее соотношение, построим итерационный процесс

Условия сходимости метода Пикара Пусть определена ограниченная область в которой правая часть уравнения удовлетворяет условия Липшица: Так как область ограничена, тогда выполняются соотношения Вычитая из итерационного соотношения уравнение с разделенными переменными, получим для погрешности Погрешность характеризует отклонение приближенного решения от точного. Оценим погрешность

Поскольку получим Так как Окончательно получим для погрешности То есть метод Пикара сходится к точному единственному решению исходной задачи.

Метод Эйлера Пусть на отрезке [a, b] ищется решение задачи Коши, построим на этом отрезке сетку с постоянным шагом h Разложим искомую функцию y(x) в ряд Тейлора вблизи произвольной точки Согласно уравнению Тогда разложение можно записать в виде Окончательно вычислительная процедура примет вид Здесь yk – результат численного решения уравнения y(xk) – точное решение исходной задачи.

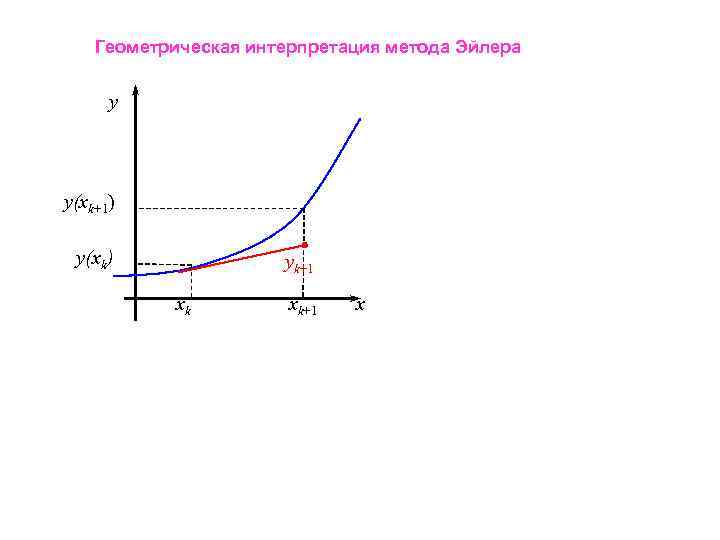
Геометрическая интерпретация метода Эйлера y y(xk+1) y(xk) yk+1 xk xk+1 x

Условия сходимости метода Эйлера Для исследования сходимости численного решения к точному запишем погреш Далее схему Эйлера запишем в виде разностного аналога Подставим в него соотношения получим Преобразуем последнее соотношение

– погрешность аппроксимации, характеризует, насколько хорошо разностный аналог аппроксимирует дифференциальное уравнение. Оценим погрешность аппроксимации. Для этого разложение в ряд Тейлора Подставим в формулу для погрешности Таким образом, погрешность имеет первый порядок аппроксимации (при ограниченной второй производной)

В общем случае порядок аппроксимации равен р, если имеет место оценка Для второго слагаемого Тогда соотношение для погрешностей преобразуется к виду Для того чтобы погрешность не возрастала Это неравенство соответствует критерию устойчивости для задачи Коши, полученному ранее

Далее, с учетом условия Липшица Учитывая условие устойчивости решения , получим тогда получим ограничение на шаг интегрирования, обеспечивающее устойчивость решения и невозрастания погрешности: Таким образом, погрешность вычислений не будет возрастать (численное решение сходится к точному), если разностная схема аппроксимирует исходное уравнение и шаг интегрирования обеспечивает устойчивость решения, т. е. из аппроксимации и устойчивости решения следует сходимость.

Скачать презентацию ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Решением, интегралом или интегральной кривой

Задача Коши.ppt

Количество слайдов: 13