Обыкновенные дифференциальные уравнения


Обыкновенные дифференциальные уравнения Первого и второго порядков

Основные понятия n Дифференциальным уравнением (ДУ) называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков искомой функции. n Общий вид ДУ: G (x, y, y´, …y(n)) = 0 n Если искомая функция зависит от одной переменной, то ДУ называется обыкновенным; если от нескольких – уравнением в частных производных. n Порядком ДУ называют порядок старшей производной, входящей в уравнение.
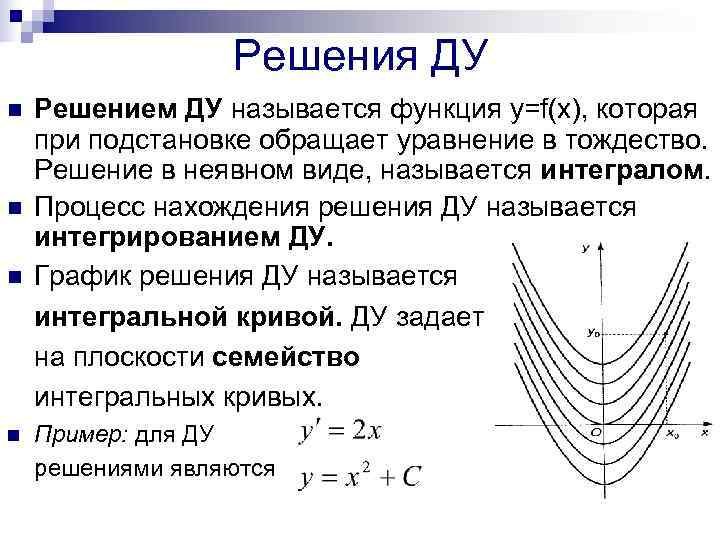
Решения ДУ n Решением ДУ называется функция y=f(x), которая при подстановке обращает уравнение в тождество. Решение в неявном виде, называется интегралом. n Процесс нахождения решения ДУ называется интегрированием ДУ. n График решения ДУ называется интегральной кривой. ДУ задает на плоскости семейство интегральных кривых. n Пример: для ДУ решениями являются

Виды решений ДУ n Общим решением (ОР) ДУ n-го порядка называется такое его решение y=φ(x, C 1, C 2, …, Cn), которое является функцией переменной х и n произвольных независимых постоянных. n ОР ДУ описывает семейство интегральных кривых n Частным решением (ЧР) ДУ называется решение, получаемое из общего решения при некоторых конкретных значениях постоянных С 1, С 2, …Сn. n ЧР ДУ задает конкретную интегральную кривую

Отыскание частного решения ДУ n Выделить одну интегральную кривую из семейства позволяют дополнительные условия: ¨ Если указана точка плоскости, через которую проходит кривая, и направление, в котором она проходит через эту точку, такие условия называются начальными или условиями Коши. Задача об отыскании частного решения ДУ, удовлетворяющего начальным условиям, называется задачей Коши. ¨ Если указаны несколько точек, через которые проходит кривая, такие условия называют граничными или краевыми. Задача отыскания частного решения, удовлетворяющего краевым условиям, называется краевой задачей.

Дифференциальные уравнения первого порядка

Основные положения n ДУ 1 -го порядка вида у´= f (x, y) называют разрешенным относительно производной. n Геометрический смысл: ДУ 1 -го порядка задает каждой точке направление касательной к интегральной кривой – поле направлений. n Решить ДУ 1 -го порядка – найти семейство кривых, отвечающих полю направлений.

Теорема Коши для ДУ 1 -го порядка n Пусть в ДУ у´= f (x, y) функция f и ее частная производная по у непрерывны в области М. Тогда 1. Для каждой точки (х0, у0) области М найдется решение у=у(х), удовлетворяющее условию у0=у(х0). 2. Если два решения у=у1(х) и у=у2(х) совпадают при х=х0, то они совпадают при всех значениях х, при которых они существуют. n Если условия Коши не выполняются, через точку либо не проходит ни одна интегральная кривая, либо проходит несколько. Такие точки называют особыми точками ДУ.

Неполные ДУ 1 -го порядка n ДУ у´= f (x, y) называется неполным, если функция f явно зависит только от х либо только от у. 1. Уравнение вида у´=f(x): 2. Уравнение вида у´=f(у) называют автономным. Его решение находят сначала в виде х=х(у): затем выражают из него у.

ДУ с разделяющимися переменными n ДУ 1 -го порядка называют уравнением с разделяющимися переменными, если оно может быть представлено в виде n Для его решения переменные и соответствующие им дифференциалы разделяют – относят в разные части равенства. Уравнение с разделенными переменными интегрируют:

Уравнения вида у´=f(ax+by) n Приводятся к уравнению с разделяющимися переменными с помощью замены z=ax+by (или z=ax+by+c, где с- некоторое число)

Однородные ДУ n ДУ 1 -го порядка называется однородным, если оно может быть представлено в виде n ДУ вида у´= f (x, y) является однородным, если функция f удовлетворяет условию f(αx, αy) = f(x, y). n Однородное уравнение сводится к уравнению с разделяющимися переменными заменой переменной

Уравнение вида n Если прямые a 1 x+b 1 y+c 1=0 и a 2 x+b 2 y+c 2=0 пересекаются в точке (р, q), то надо произвести замену переменных s = x-p, t = y-q. Относительно новых переменных уравнение будет однородным. n Если прямые не пересекаются, уравнение сводится к однородному заменой z = a 1 x+b 1 y.

Линейные ДУ 1 -го порядка n ДУ 1 -го порядка называется линейным, если оно имеет вид где f(x) и g(x) – непрерывные функции аргумента х n Если g(x)≡ 0, то уравнение называют однородным; иначе – неоднородным. n Решение ЛДУ можно найти в виде где - любое решение уравнения - общее решение уравнения

Уравнение Бернулли n ДУ 1 -го порядка называется уравнением Бернулли, если оно имеет вид где n≠ 0, n≠ 1. n Уравнение Бернулли сводится к линейному подстановкой или может быть решено тем же методом, что и линейные ДУ.

Дифференциальные уравнения второго порядка

Основные положения n ДУ 2 -го порядка называется уравнение вида F(x, y, y´´)=0. n Будем рассматривать уравнение y´´= f (x, y, y´) – разрешенное относительно второй производной. n Теорема Коши для ДУ 2 -го порядка: Пусть функция f(x, y, y´) и ее частные производные по у и у´ непрерывны в области М. Тогда для любой точки М 0(х0, у0´) существует и единственное решение, удовлетворяющее начальным условиям у(х0)=у0, у´(х0)=у0´

Неполные ДУ 2 -го порядка n Уравнение вида y´´= f(x) (содержит только х) заменой z(x)=y´ сводится к решению двух ДУ 1 -го порядка z´=f(x) и y´=z(x). n Уравнение вида y´´= f(x, y´) (не содержит у) заменой z(x)=y´ сводится к решению двух ДУ 1 -го порядка z´=f(x, z) и y´=z(x). n Уравнение вида y´´= f(y, y´) (не содержит х) заменой z(y)=y´ сводится к решению двух ДУ 1 -го порядка z·z´=f(y, z) и y´=z(y).

Линейные ДУ 2 -го порядка с постоянными коэффициентами n Линейное ДУ 2 -го порядка с постоянными коэффициентами имеет вид где p, q – некоторые числа, r(x) – функция. n Если r(x)≡ 0, то уравнение называется однородным (ЛОДУ); в противном случае – неоднородным (ЛНДУ).

Линейные однородные ДУ 2 -го порядка (ЛОДУ) n Рассмотрим ЛОДУ (*) n Заменим в нем каждую производную соответствующей степенью неизвестной k. n Уравнение вида (^) называется характеристическим для ЛОДУ (*)

Вид общего решения ЛОДУ Если характеристическое уравнение (^) имеет: n два различных действительных корня k 1 и k 2, то общее решение (*) имеет вид n два совпавших действительных корня k 1= k 2= k, то общее решение (*) имеет вид n два сопряженных комплексных корня k 1=a+bi и k 2=a-bi, то общее решение (*) имеет вид

Неоднородное линейное ДУ 2 -го порядка (ЛНДУ) n ЛНДУ 2 -го порядка с постоянными коэффициентами имеет вид где p, q – некоторые числа, r(x) – функция. n Теорема о структуре решения ЛНДУ: Общее решение ЛНДУ есть сумма его частного решения и общего решения соответствующего ЛОДУ: ОРЛНДУ = ЧРЛНДУ + ОРЛОДУ

Частное решение ЛНДУ n Если функция - многочлен степени n, то ЧРЛНДУ имеет вид где s равен кратности корня х = 0 в характеристическом уравнении. n Если функция r(x) имеет вид то ЧРЛНДУ имеет вид где s - показатель кратности корня х = α в характеристическом уравнении.

Частное решение ЛНДУ n Если функция то ЧРЛНДУ имеет вид где n Если функция r(x) является суммой функций то его частное решение имеет вид где ui – частное решение соответствующего уравнения

Частное решение ЛНДУ n Все рассмотренные случаи являются частностями для функции вида где α и β – любые действительные числа, f(x) и g(x) – многочлены с действительными коэффициентами. n Частное решение ЛНДУ с такой правой частью следует искать в виде где s – показатель кратности корня х=α+iβ в характеристическом уравнении, v(x) и w(x)- многочлены наибольшей из степеней f(x) и g(x) с неопределенными коэффициентами (их находят подстановкой v(x) и w(x) в исходное уравнение)

