Обучение без учителя С к Распознавание образов Простой

Обучение без учителя С/к «Распознавание образов»

Простой алгоритм выявления кластеров Обучение без учителя

Простой алгоритм выявления кластеров n Пусть задано множество N образов {x 1, x 2, …, x. N}. n Пусть центр первого кластера z 1 совпадает с любым из заданных образов и определена произвольная неотрицательная пороговая величина T; n Будем считать, что z 1 =x 1. n Вычислим расстояние D 21 между образом x 2 и центром кластера z 1 по формуле евклидова расстояния D = ||x-zi|| (1) n Если это расстояние больше пороговой величины T, то учреждается новый центр кластера z 2=x 2.

n В противном случае образ x 2 включается в n n кластер, центром которого является z 1. Если условие D 21 > T выполнено, то z 2 является центром нового кластера. Далее вычисляются расстояния D 31 и D 32 до центров кластеров z 1 и z 2. Если оба расстояния оказываются больше порогового значения T , то учреждается новый центр кластера z 3=x 3. В противном случае x 3 зачисляется в тот кластер, чей центр ему ближе.

n Аналогично вычисляются расстояния от каждого нового образа xi до каждого известного центра кластера zi и сравниваются с пороговой величиной T, если все эти расстояния превосходят значения порога T, то учреждается центр кластера. n В противном случае образ зачисляется в кластер с самым близким к нему центром. n Результаты описанной процедуры определяются: n n Выбором первого центра кластера; Порядком обхода образов; Значением пороговой величины T; Геометрическими характеристиками данных.

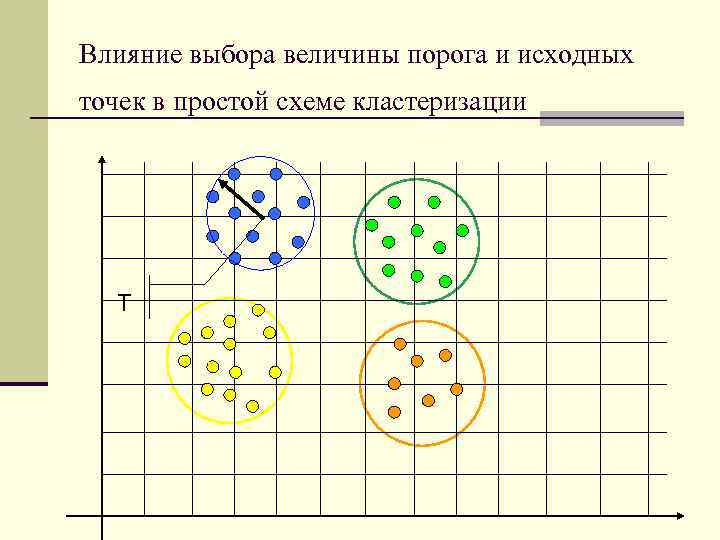
Влияние выбора величины порога и исходных точек в простой схеме кластеризации Т

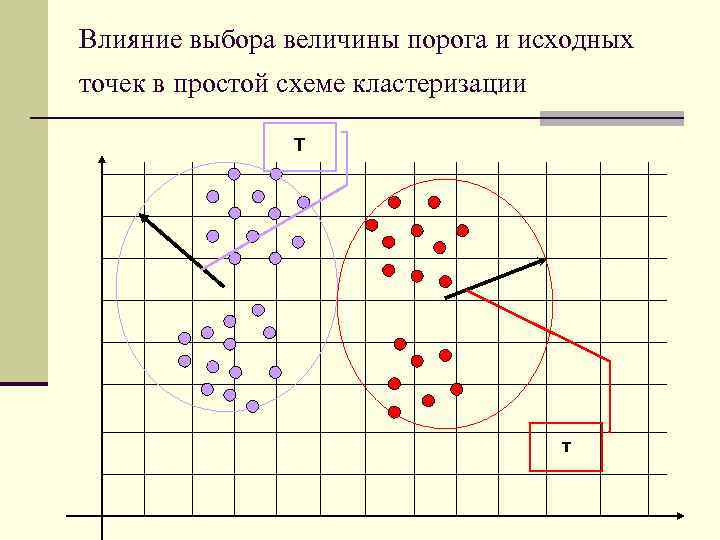
Влияние выбора величины порога и исходных точек в простой схеме кластеризации Т т

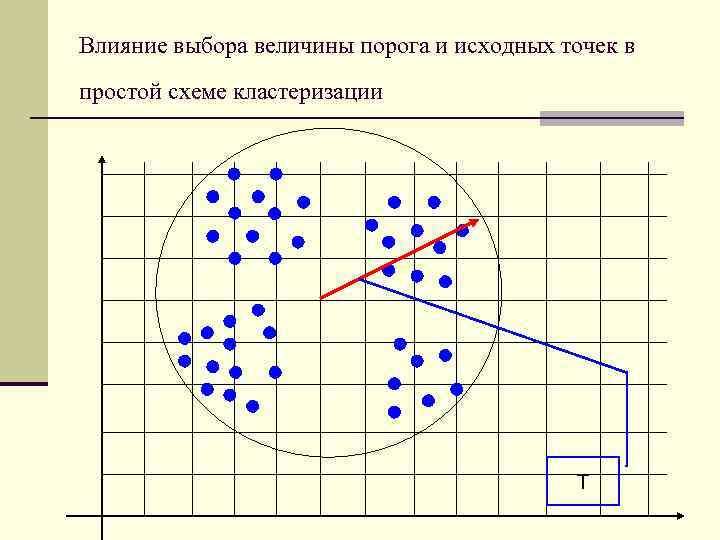
Влияние выбора величины порога и исходных точек в простой схеме кластеризации Т

n Алгоритм обладает рядом очевидных недостатков, тем не менее он позволяет быстро и просто получить приблизительные оценки основных характеристик заданного набора данных. n Алгоритм привлекателен с вычислительной точки зрения, поскольку для выявления центра кластеров, соответствующих заданному порогу Т, ему требуется только однократный просмотр выборки.

n Для того, чтобы процедура выполняла эффективную кластеризацию, необходимо выполнять большое количество экспериментов, варьируя значения порогов и центров кластеров. n Важными характеристиками эффективности проведённого эксперимента являются: n n Расстояния разделяющие центры кластеров; Количества образов вошедших в различные кластеры; Ближайшая и наиболее удалённая от центра точки кластера; Различие размеров отдельных кластеров.

n Информацию, полученную после каждого цикла обработки данных , можно использовать для коррекции: n Значения порога Т; n Новой исходной точки кластеризации. n Можно рассчитывать на получение с помощью подобной процедуры полезных результатов, когда в данных имеются характерные «гнёзда» , которые достаточно хорошо разделяются при соответствующем выборе значения порога.

Алгоритм максимина Обучение без учителя

n Алгоритм максиминного расстояния представляет собой ещё одну эвристическую процедуру, которая использует евклидово расстояние. n Алгоритм аналогичен предыдущему, однако в первую очередь он выявляет наиболее удалённые кластеры. n Рассмотрим алгоритм максиминного расстояния на примере: n Дана выборка из 10 двумерных образов рис. 1. n Даны таблицы, в которых содержатся выборочные образы и центры кластеров, полученных в результате выполнения алгоритма (рис. 2. ).

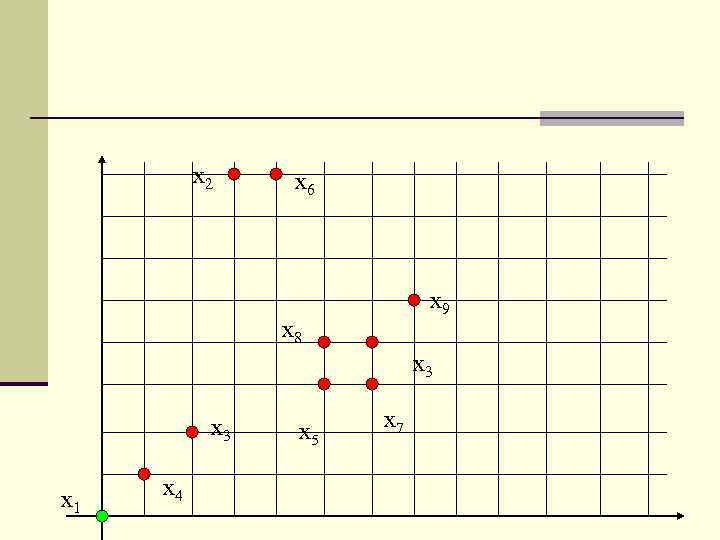
x 2 x 6 x 9 x 8 x 3 x 1 x 4 x 5 x 7

n Шаг 1. Выбор произвольным образом центра кластера. Пусть это будет x 1. См. табл. 1. n Шаг 2. Вычисляем расстояния d 1 i(z 1, xi). Отыскиваем образ, отстоящий от образа x 1 на наибольшее расстояние, а именно, находим max(d 1 i(z 1, xi)). В данном случае это будет x 6. Образ x 6 назначается центром кластера z 2. n Шаг 3. Вычисляем расстояния между центрами кластеров z 1 и z 2 и всеми образами. В каждой паре этих расстояний вычисляем минимальное:

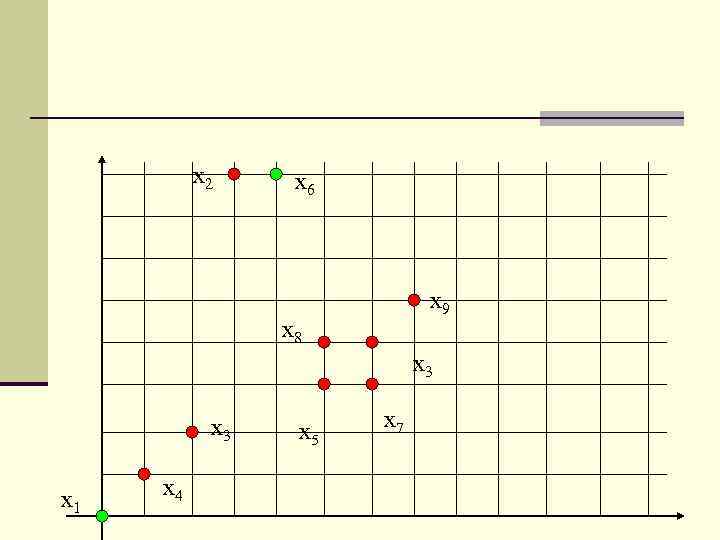
x 2 x 6 x 9 x 8 x 3 x 1 x 4 x 5 x 7

gr=Minr(d(xr, z 1), d(xr, z 2)), r=1. . (n-2); n Шаг 4. Находим максимальное расстояние из этих минимальных: L = Max(g 1, g 2, …, gn-2) n Если L > ½ d(z 1, z 2), то соответствующий образ назначается центром кластера z 3; n В противном случае выполнение алгоритма прекращается. В приведённом примере центом кластера является образ x 7.

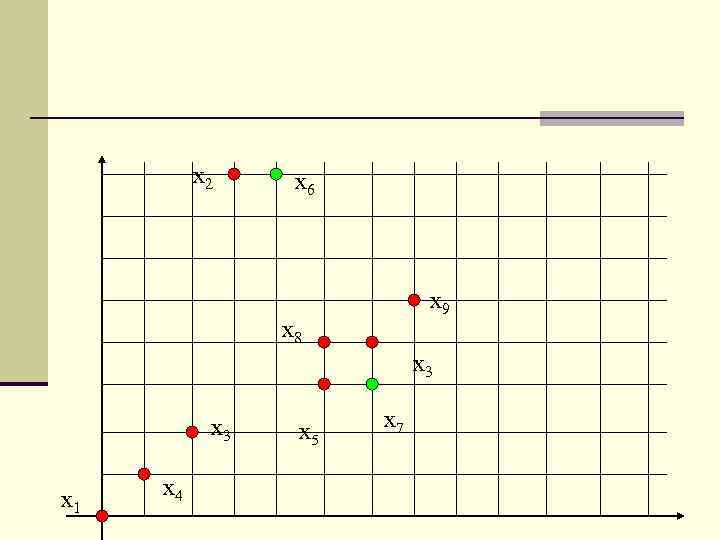
x 2 x 6 x 9 x 8 x 3 x 1 x 4 x 5 x 7

n Шаг 5. На следующем шаге вычисляются расстояния между тремя выделенными кластерами и всеми остальными образами. В каждой группе из трёх расстояний выбирается минимальное: gr=Minr(d(xr, z 1), d(xr, z 2), d(xr, z 3)), r=1. . (n-3); n Шаг 6. На следующем шаге вычисляются максимальное из этих расстояний: L = Max(g 1, g 2, …, gn-3)

n Если L составляет большую часть «типичных» n n предыдущих максимальных состояний, то соответствующий образ назначается центром кластера z 4; В противном случае выполнение алгоритм прекращается. Хорошей мерой оценки предыдущих максимальных расстояний является их среднее значение. В конкретном примере, который мы рассматриваем, максимальным расстоянием оказалось расстояние между образами x 1 и x 3. Это расстояние не удовлетворяет принятому условию. На данном шаге работа алгоритма прекращается.

n В общем случае работа алгоритма прекращается, когда на определённом шаге алгоритма максимальное расстояние не соответствует условию выделения нового кластера. n В предыдущем примере было выделено три кластера x 1, x 6 и x 7. n Классифицируемые образы относят к кластеру, центр которого для него ближайший. n Таким образом, в нашем примере были выделены три кластера: {x 1, x 3, x 4} {x 2, x 6} {x 5 x 7 x 8 , x 8, x 9}

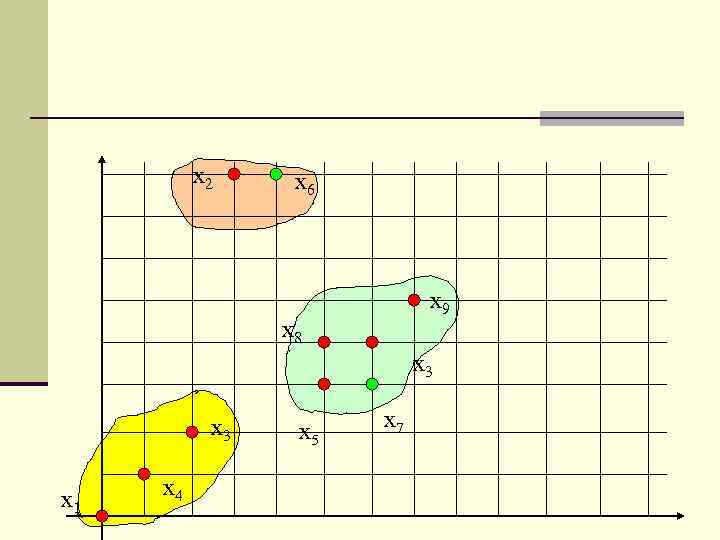
x 2 x 6 x 9 x 8 x 3 x 1 x 4 x 5 x 7

Алгоритм К внутригрупповых средних Обучение без учителя

n Шаг 1. Выбираются К исходных центров кластеров z 1(1), z 2(1), …, z. К(1). Этот выбор выполняется произвольно, обычно в качестве исходных центров используют первые К результатов выборки из заданного множества образов. n Шаг 2. На к шаге итерации заданное множество образов {x} распределяется по к кластерам по следующему правилу: x Sj(k), если ||x-zj(k)|| < ||x-zi(k)||, для всех i=1, 2, …, K, i j, где Sj(k) – множество образов, входящих в кластер с центром zj(k).

n Если ||x-zj(k)|| = ||x-zi(k)||, то решение принимается произвольным образом. n Шаг 3. На основе результатов шага 2 образуются центры новых кластеров zj(k+1), j = 1, 2, …, k); Центры образуются исходя из условия, что сумма квадратов расстояния между всеми образами и новым центром должна быть минимальна. Другими словами, новые центры кластеров выбираются таким образом, чтобы минимизировать показатель качества: n Jj = ||x-zj(k+1)||2 , x Sj(k), j = 1, 2, …, k

n Центр zj(k+1) является по сути дела выборочным средним, определенным по множеству Sj(k). Следовательно, новые центры кластеров определяются по формуле: n zj(k+1) = 1/Nj x, x Sj(k), j = 1, 2, …, k , где Nj – число выборочных образов, входящих в множество Sj(k). n Шаг 4. Равенство zj(k+1) = zj(k) является при j = 1, 2, …, k является условием сходимости алгоритма. При достижении этого условия алгоритм завершается. В противном случае алгоритм повторяется от шага 2.

n Качество работы алгоритмов, основанных на вычислении К внутригрупповых средних, зависит от: n n Числа выбираемых центров кластеров; От выбора исходных центров кластеров; От последовательности осмотра образов; От геометрической особенности данных. n Приемлемых результатов можно ожидать, если данные представляют собой характерные «гроздья» , отстоящие друг от друга на значительное расстояние.

n Практическое применение этого метода потребует ряда экспериментов, связанных с: n Выбором различных значений К; n Выбором исходного расположения центров кластеров. n Пример: n Шаг 1. Задаётся К=2 и выбирается z 1(1)= x 1=(0, 0)’, z 2(1)= x 2=(1, 0)’.

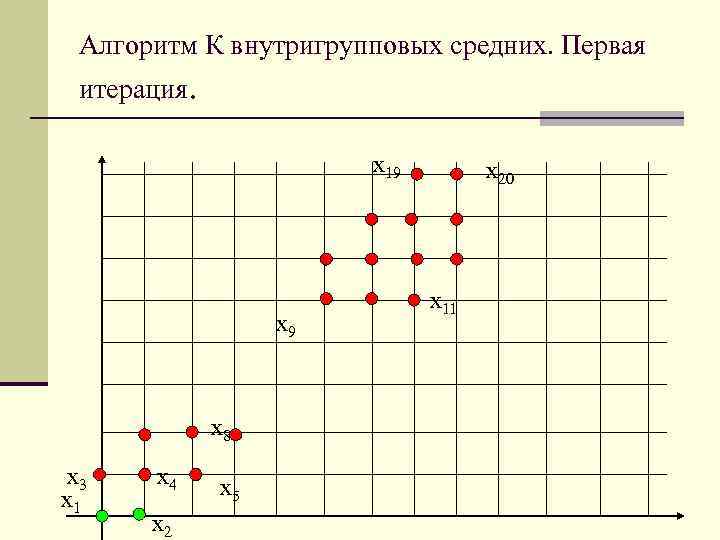
Алгоритм К внутригрупповых средних. Первая итерация. x 19 x 8 x 3 x 1 x 4 x 2 x 5 x 20 x 11

n Шаг 2. Поскольку ||x 1 -z 1(1)|| < ||x 1 -zi(1)|| и ||x 3 -z 1(1)|| < ||x 1 -zi(1)||, i = 2, то S 1(1) = {x 1, x 3}. Аналогичным образом устанавливаем, что остальные образы расположены ближе к образу z 2(1) и S 2(1) = {x 2, x 4, x 2, x 5, …, x 20}. n Шаг 3. Коррекция назначения центров кластеров: n Z 1(2) = 1/N 1 x, x S 1(1) = ½ (x 1+x 3) = (0, 0; 0, 5) n Z 2(2) = 1/N 2 x, x S 2(1) = 1/18 (x 2+x 4+…+x 20) = (5, 67; 5, 33)

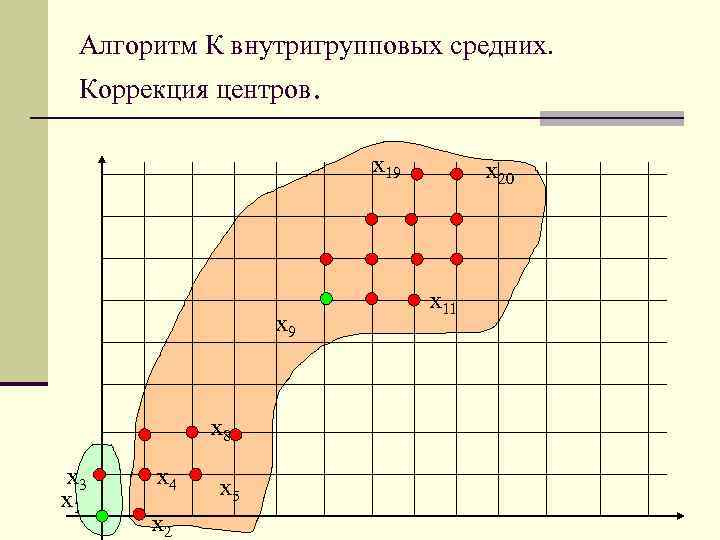
Алгоритм К внутригрупповых средних. Коррекция центров. x 19 x 8 x 3 x 1 x 4 x 2 x 5 x 20 x 11

n Шаг 4. Т. к. Z 1(2) Z 1(1), то возврат к шагу 2. n Шаг 2. Поскольку ||xl-z 1(2)|| < ||xl-z 2(2)||, l= 1, 2, …, 8 и ||xl-z 2(2)|| < ||x 1 -z 1(2)||, l = 9, 10, …, 20, то S 1(2) = {x 1, …, x 8}. Аналогичным образом устанавливаем, что S 2(2) = {x 9, x 10, …, x 20}. n Шаг 3. Коррекция назначения центров кластеров: n Z 1(3) = 1/N 1 x, x S 1(2) = 1/8 (x 1+x 2 +…+x 8) = (1, 25; 1, 13) n Z 2(3) = 1/N 2 x, x S 2(2) = 1/12 (x 9+x 10+…+x 20) = (7, 67; 7, 33)

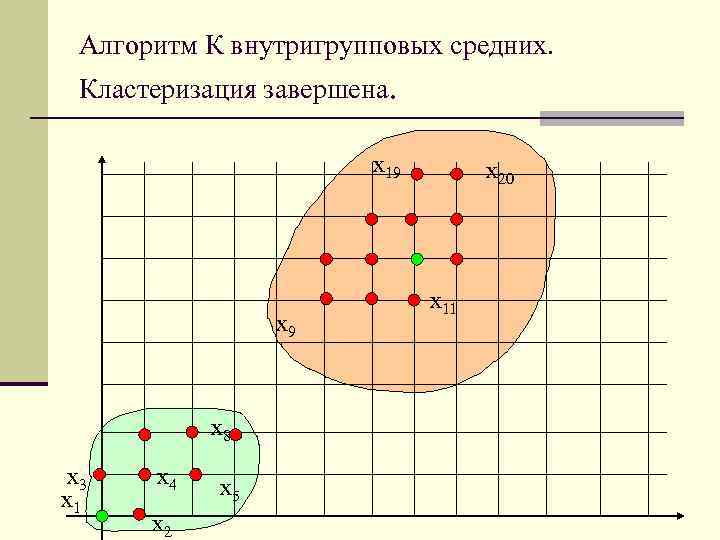
Алгоритм К внутригрупповых средних. Кластеризация завершена. x 19 x 8 x 3 x 1 x 4 x 2 x 5 x 20 x 11

n Шаг 4. Т. к. Z 1(3) Z 1(2), то возврат к шагу 2. n Шаг 2. Получаем те же самые результаты, что и n n на предыдущей итерации: Z 1(4) = Z 1(3), Z 2(4)= Z 2(3). Шаг 3. Коррекция назначения центров кластеров – получаем те же самые результаты. Шаг 4. Т. к. Zj(4) Zj(3), j=1, 2, алгоритм сошелся, получаем следующие центры кластеров: Z 1 = (1, 25; 1, 13) Z 2= (7, 67; 7, 33)