a5a28a855b81c220f30e046e64c03686.ppt
- Количество слайдов: 100

Obtaining an NMR Spectra Basic Requirements: NMR sample: compound of interest dissolved in 500 -600 ml of deuterated solvent. Ø Higher the concentration higher the sensitivity Magnet: differentiate spin states (aligned/unaligned). Ø Higher the field strength higher the sensitivity and resolution Ø Requires homogeneous field over the sample RF electronics: generate RF pulse to perturb system equilibrium and observe NMR signal. Ø Requires accurate control of pulse power and duration Ø Stability of pulse Receiver electronics: detection of induced current from nuclear precesson Ø Requires high sensitivity Ø Conversion of analog signal to digital signal
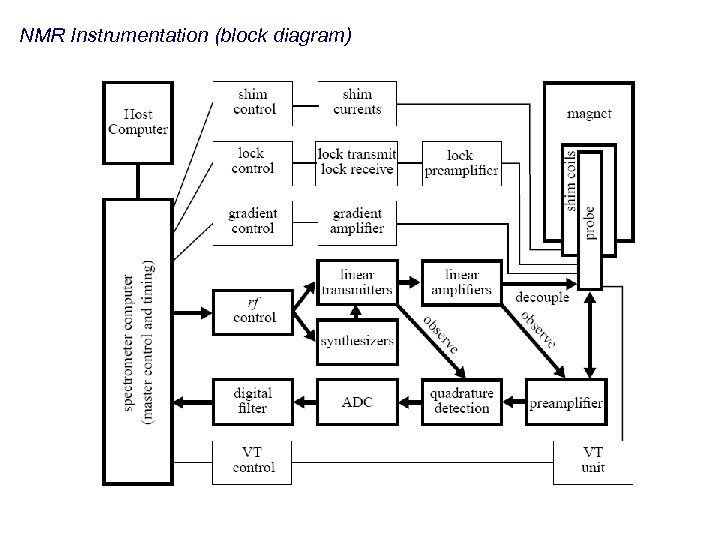
NMR Instrumentation (block diagram)
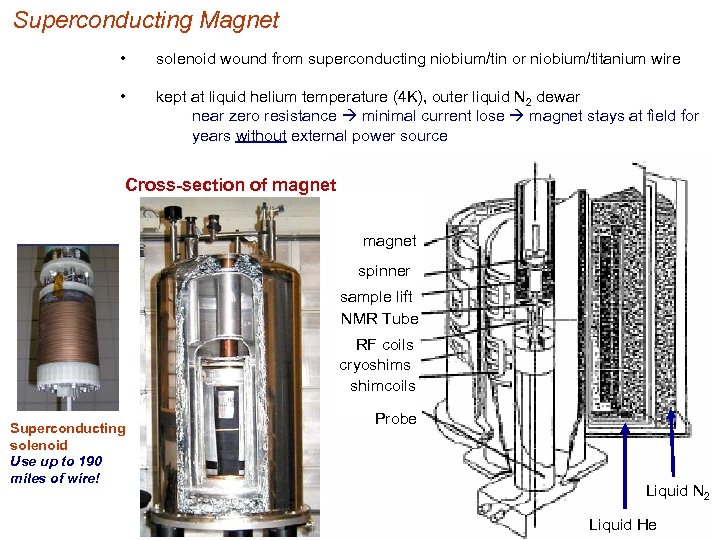
Superconducting Magnet • solenoid wound from superconducting niobium/tin or niobium/titanium wire • kept at liquid helium temperature (4 K), outer liquid N 2 dewar near zero resistance minimal current lose magnet stays at field for years without external power source Cross-section of magnet spinner sample lift NMR Tube RF coils cryoshims shimcoils Superconducting solenoid Use up to 190 miles of wire! Probe Liquid N 2 Liquid He

NMR Sample Factors to Consider: • • • Maximize sample concentration − Avoid precipitation or aggregation Use a single deuterated solvent − Reference for lock Avoid heterogeneous samples distorts magnetic field homogeneity − Avoid air bubbles, suspended particles, sample separation Avoid low quality NMR tubes distorts magnetic field homogeneity − Breaks easily damage the NMR probe Chose appropriate temperature for the sample − Freezing or boiling the sample may break the NMR tube and damage the NMR probe. Properly position NMR sample in the magnet − Position sample in homogeneous region of magnet and between detection and RF coils − Avoid positioning meniscus close to coil edge distorts magnetic field homogeneity Frequency of absorption: n = g Bo / 2 p
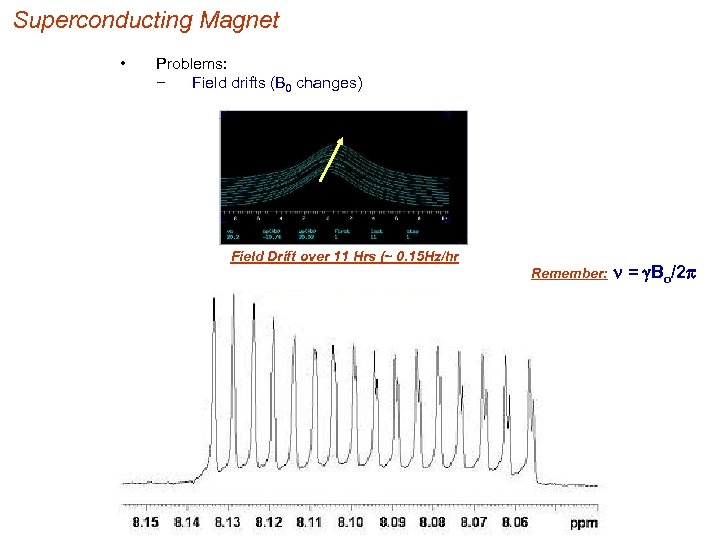
Superconducting Magnet • Problems: − Field drifts (B 0 changes) Field Drift over 11 Hrs (~ 0. 15 Hz/hr Remember: n = g. Bo/2 p
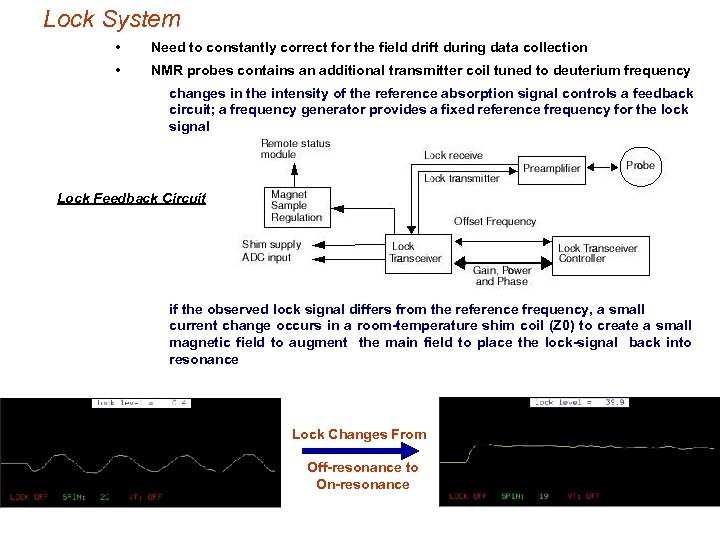
Lock System • Need to constantly correct for the field drift during data collection • NMR probes contains an additional transmitter coil tuned to deuterium frequency changes in the intensity of the reference absorption signal controls a feedback circuit; a frequency generator provides a fixed reference frequency for the lock signal Lock Feedback Circuit if the observed lock signal differs from the reference frequency, a small current change occurs in a room-temperature shim coil (Z 0) to create a small magnetic field to augment the main field to place the lock-signal back into resonance Lock Changes From Off-resonance to On-resonance
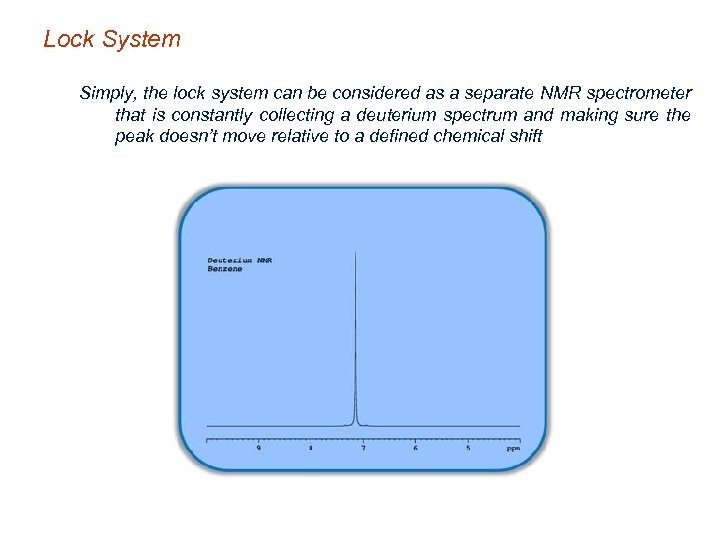
Lock System Simply, the lock system can be considered as a separate NMR spectrometer that is constantly collecting a deuterium spectrum and making sure the peak doesn’t move relative to a defined chemical shift
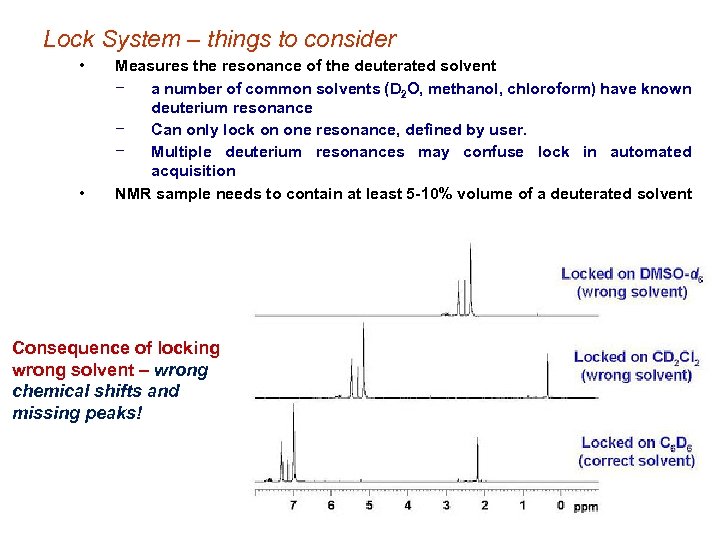
Lock System – things to consider • • Measures the resonance of the deuterated solvent − a number of common solvents (D 2 O, methanol, chloroform) have known deuterium resonance − Can only lock on one resonance, defined by user. − Multiple deuterium resonances may confuse lock in automated acquisition NMR sample needs to contain at least 5 -10% volume of a deuterated solvent Consequence of locking wrong solvent – wrong chemical shifts and missing peaks!

Lock System – things to consider • Maximize lock signal indicates on-resonance − • Use lock signal to shim sample Loss of lock during experiment is problematic data not reliable − − Instrument problem − • NMR sample degraded Started with weak lock signal Increase lock signal by increasing lock gain − − • Amplification of the detected lock signal Increases both signal and noise, so higher lock gain noisier lock signal Increase lock signal by increasing lock power − Strength of RF pulse to detect lock signal o Too high and lock signal is saturated intensity of lock signal fluctuates up and down o Too low and lock signal may not be observable
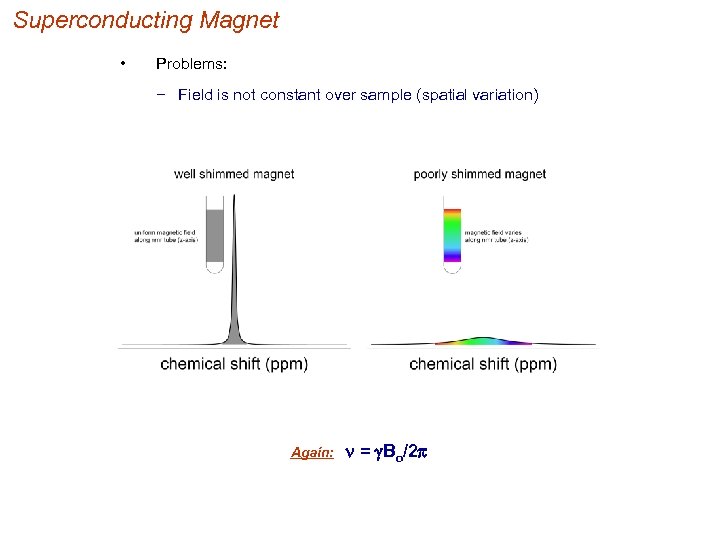
Superconducting Magnet • Problems: − Field is not constant over sample (spatial variation) Again: n = g. Bo/2 p
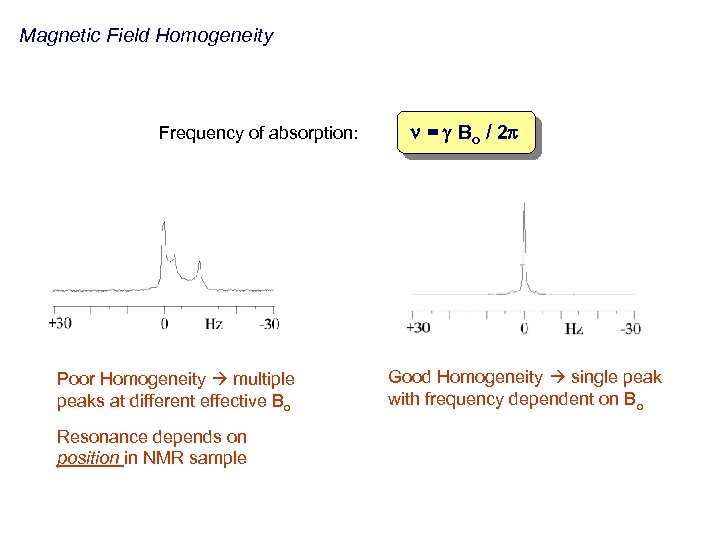
Magnetic Field Homogeneity Frequency of absorption: Poor Homogeneity multiple peaks at different effective Bo Resonance depends on position in NMR sample n = g Bo / 2 p Good Homogeneity single peak with frequency dependent on Bo
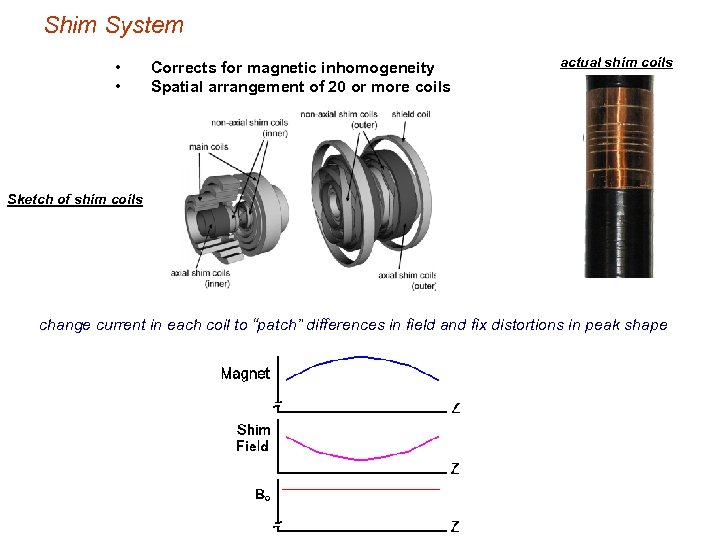
Shim System • • Corrects for magnetic inhomogeneity Spatial arrangement of 20 or more coils actual shim coils Sketch of shim coils change current in each coil to “patch” differences in field and fix distortions in peak shape
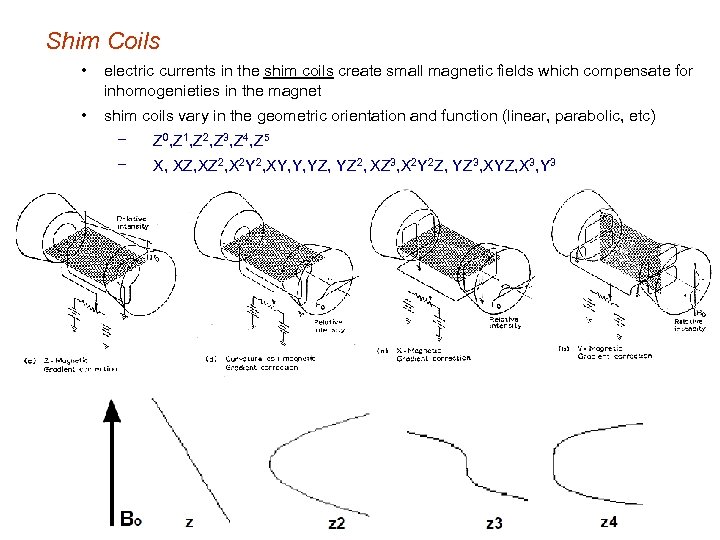
Shim Coils • electric currents in the shim coils create small magnetic fields which compensate for inhomogenieties in the magnet • shim coils vary in the geometric orientation and function (linear, parabolic, etc) − Z 0, Z 1, Z 2, Z 3, Z 4, Z 5 − X, XZ 2, X 2 Y 2, XY, Y, YZ 2, XZ 3, X 2 Y 2 Z, YZ 3, XYZ, X 3, Y 3
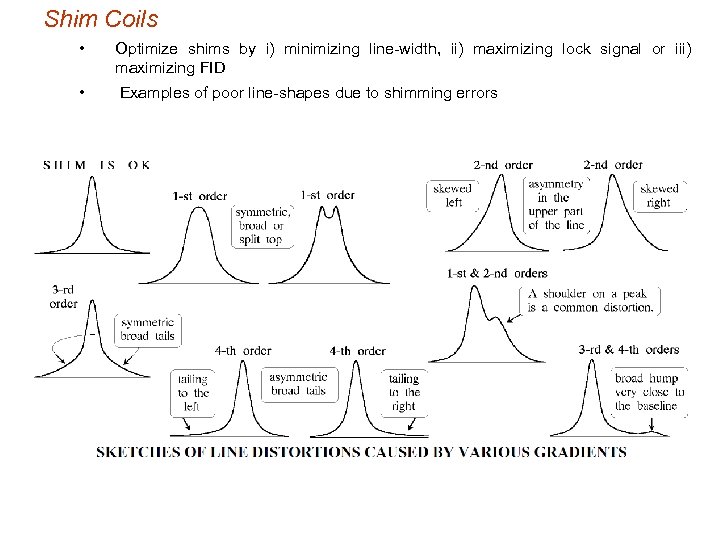
Shim Coils • Optimize shims by i) minimizing line-width, ii) maximizing lock signal or iii) maximizing FID • Examples of poor line-shapes due to shimming errors
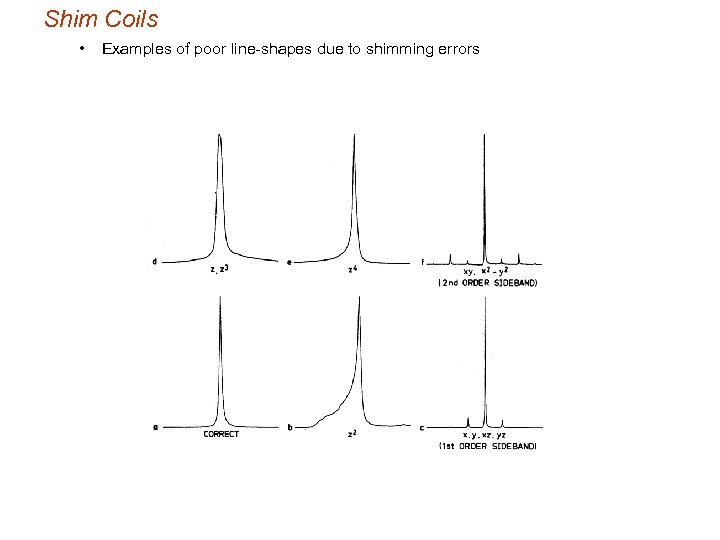
Shim Coils • Examples of poor line-shapes due to shimming errors

Shim Coils • Examples of poor FID shape due to shimming errors Perfectly Shimmed Magnet Mis-shimmed Magnet
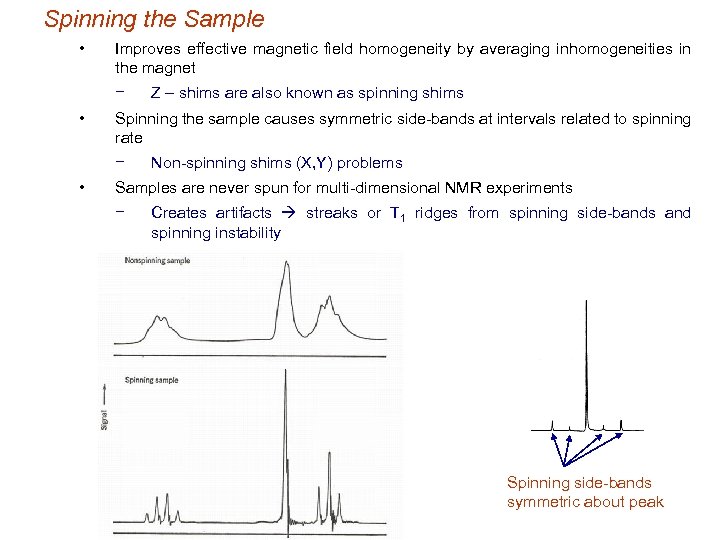
Spinning the Sample • Improves effective magnetic field homogeneity by averaging inhomogeneities in the magnet − • Spinning the sample causes symmetric side-bands at intervals related to spinning rate − • Z – shims are also known as spinning shims Non-spinning shims (X, Y) problems Samples are never spun for multi-dimensional NMR experiments − Creates artifacts streaks or T 1 ridges from spinning side-bands and spinning instability Spinning side-bands symmetric about peak

Gradient Shimming • Use pulse field gradients to automate the shimming (Top. Shim) − Gradients - spatial changes to B 0 • Gradients are used to probe (map) the Field (B 0) profile • A Shim Map is unique to each probe • Requires a Strong Signal (Solvent) − Requires H 2 O+D 2 O, CH 3 CN+D 2 O or CH 3 OH+D 2 O solvent Shim Map
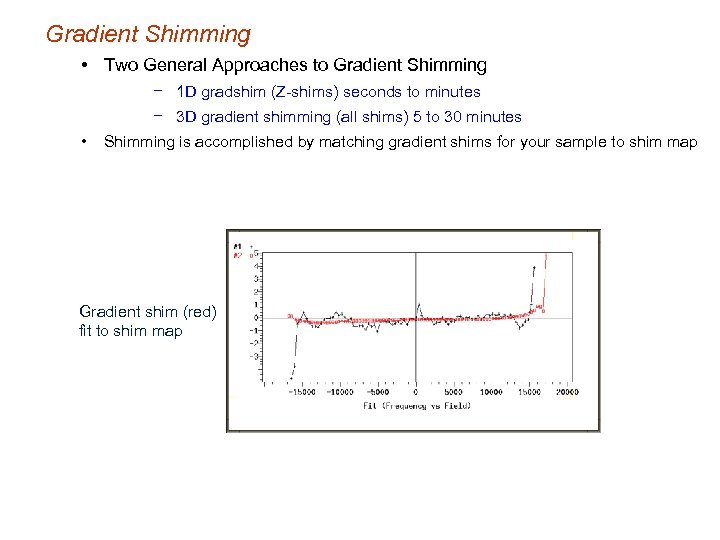
Gradient Shimming • Two General Approaches to Gradient Shimming − 1 D gradshim (Z-shims) seconds to minutes − 3 D gradient shimming (all shims) 5 to 30 minutes • Shimming is accomplished by matching gradient shims for your sample to shim map Gradient shim (red) fit to shim map
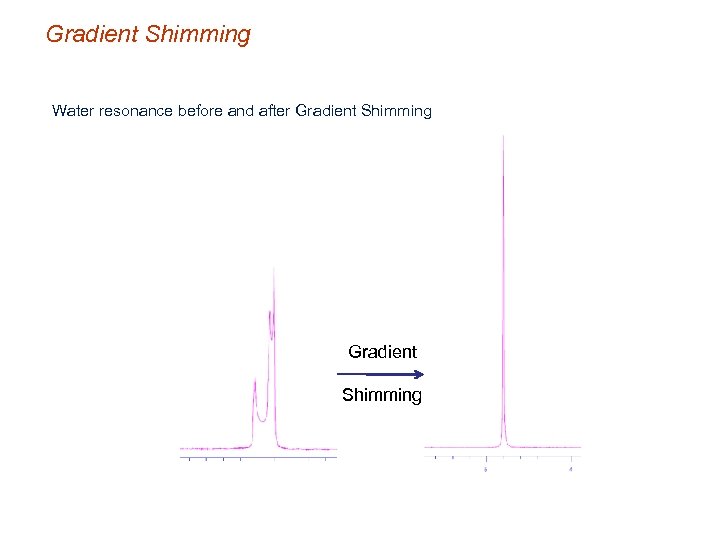
Gradient Shimming Water resonance before and after Gradient Shimming
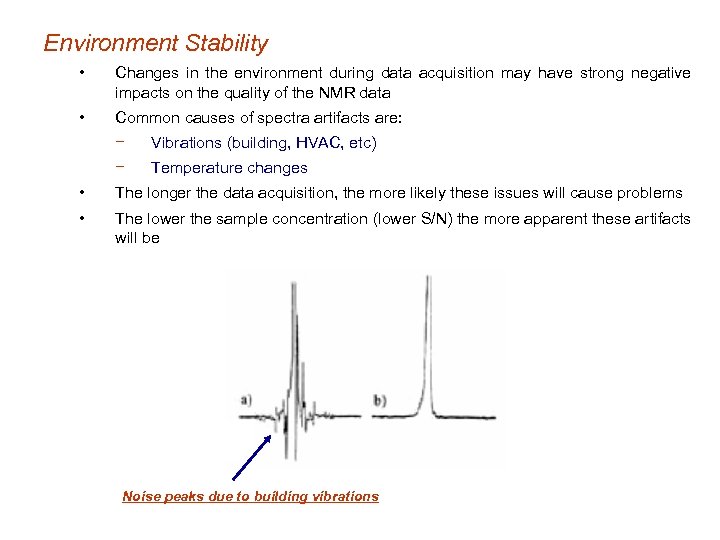
Environment Stability • Changes in the environment during data acquisition may have strong negative impacts on the quality of the NMR data • Common causes of spectra artifacts are: − Vibrations (building, HVAC, etc) − Temperature changes • The longer the data acquisition, the more likely these issues will cause problems • The lower the sample concentration (lower S/N) the more apparent these artifacts will be Noise peaks due to building vibrations
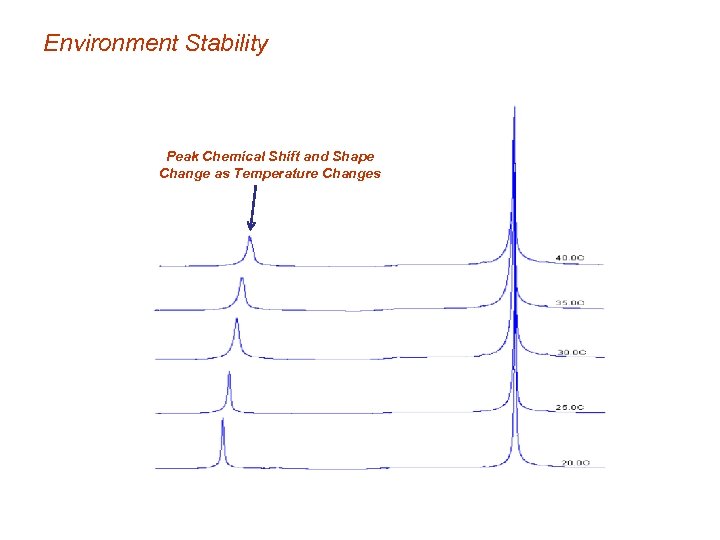
Environment Stability Peak Chemical Shift and Shape Change as Temperature Changes
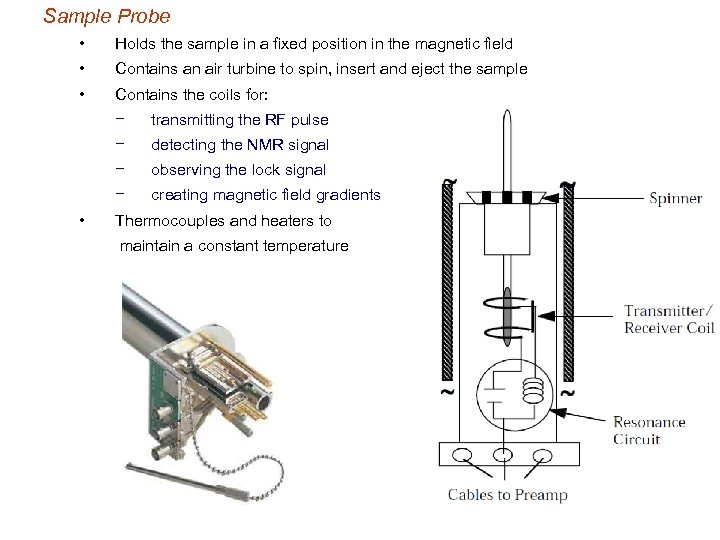
Sample Probe • Holds the sample in a fixed position in the magnetic field • Contains an air turbine to spin, insert and eject the sample • Contains the coils for: − − detecting the NMR signal − observing the lock signal − • transmitting the RF pulse creating magnetic field gradients Thermocouples and heaters to maintain a constant temperature

Sample Probe Important to note, because of the high magnetic field, the probe has to be built with nonmagnetic material such as glass and plastics. Thus, probes tend to be fragile and easy to break
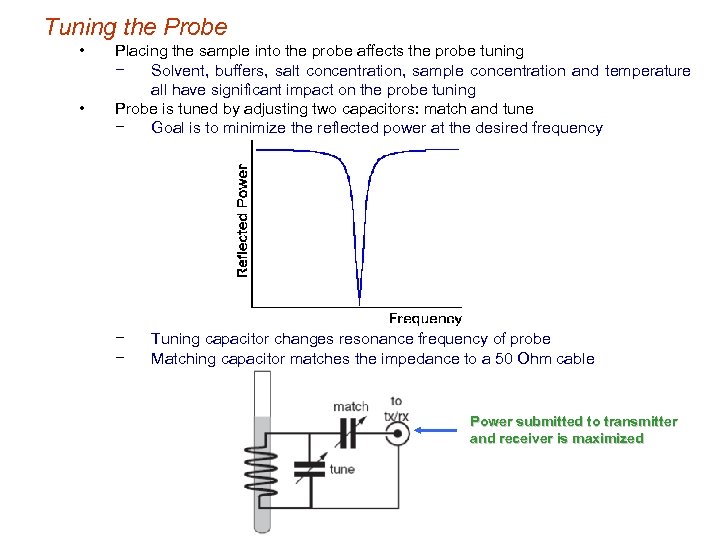
Tuning the Probe • • Placing the sample into the probe affects the probe tuning − Solvent, buffers, salt concentration, sample concentration and temperature all have significant impact on the probe tuning Probe is tuned by adjusting two capacitors: match and tune − Goal is to minimize the reflected power at the desired frequency − − Tuning capacitor changes resonance frequency of probe Matching capacitor matches the impedance to a 50 Ohm cable Power submitted to transmitter and receiver is maximized
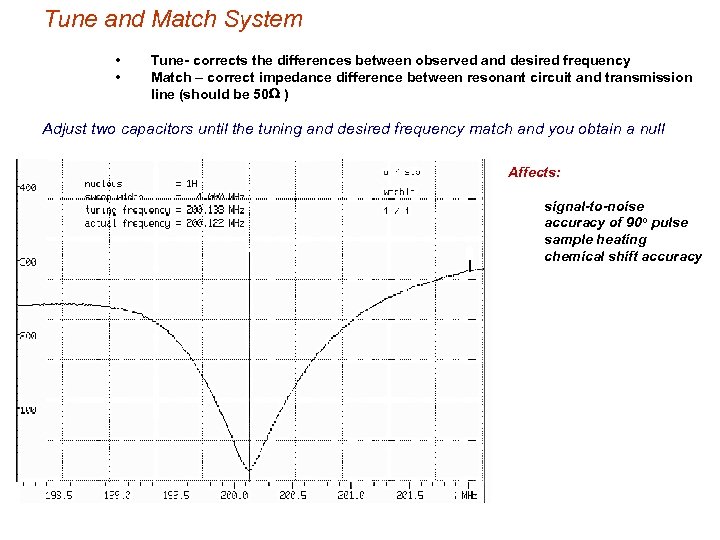
Tune and Match System • • Tune- corrects the differences between observed and desired frequency Match – correct impedance difference between resonant circuit and transmission line (should be 50 W ) Adjust two capacitors until the tuning and desired frequency match and you obtain a null Affects: signal-to-noise accuracy of 90 o pulse sample heating chemical shift accuracy
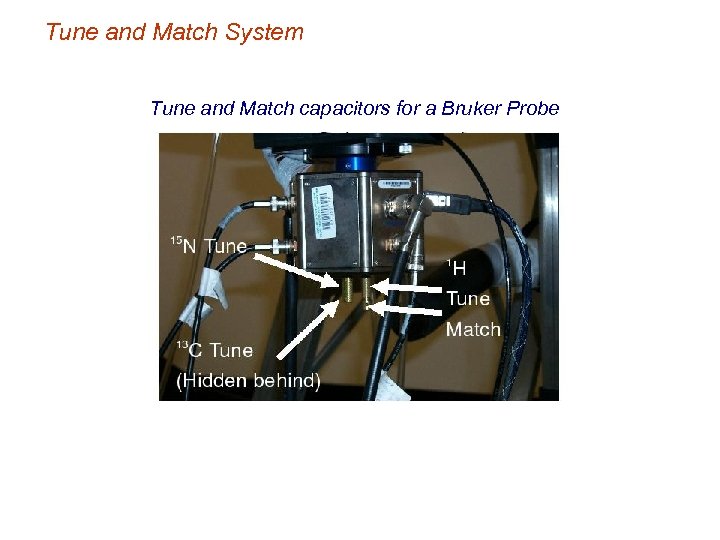
Tune and Match System Tune and Match capacitors for a Bruker Probe

Tune and Match System Changing the Distance Between the Plates or the Amount of Plate Surface Area which overlaps in a Variable Capacitor Physical limits to how far the capacitor can be turned in either direction. If turned too far will easily break!!
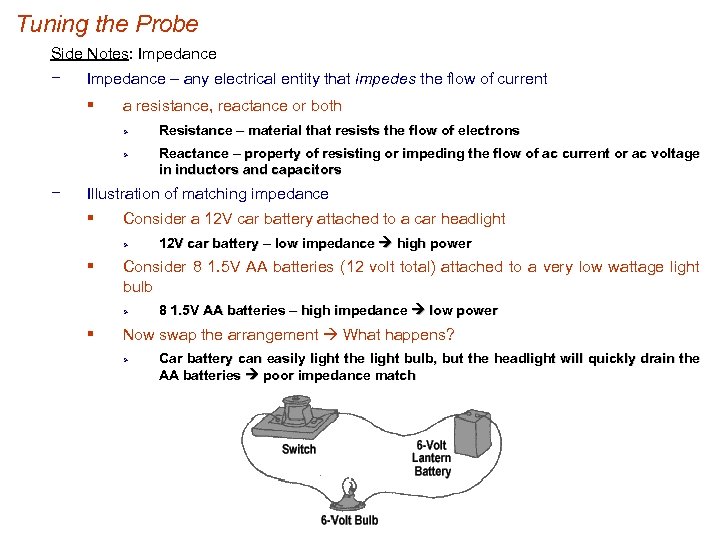
Tuning the Probe Side Notes: Impedance − Impedance – any electrical entity that impedes the flow of current § a resistance, reactance or both Ø Ø − Resistance – material that resists the flow of electrons Reactance – property of resisting or impeding the flow of ac current or ac voltage in inductors and capacitors Illustration of matching impedance § Consider a 12 V car battery attached to a car headlight Ø § Consider 8 1. 5 V AA batteries (12 volt total) attached to a very low wattage light bulb Ø § 12 V car battery – low impedance high power 8 1. 5 V AA batteries – high impedance low power Now swap the arrangement What happens? Ø Car battery can easily light the light bulb, but the headlight will quickly drain the AA batteries poor impedance match
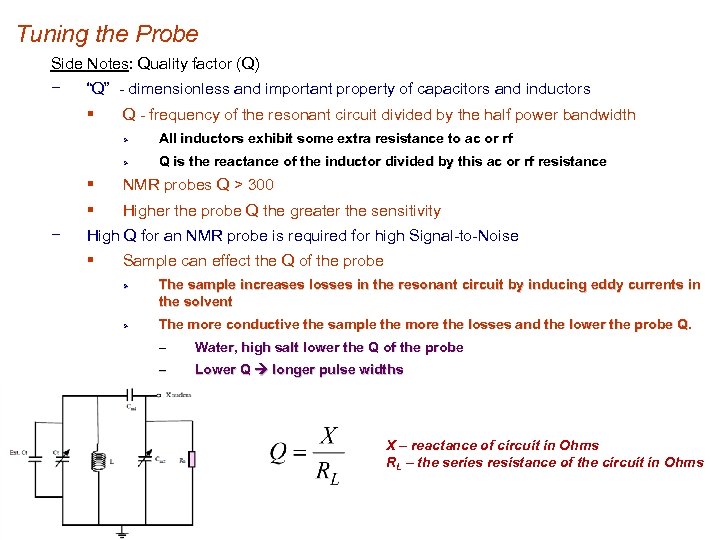
Tuning the Probe Side Notes: Quality factor (Q) − “Q” - dimensionless and important property of capacitors and inductors § Q - frequency of the resonant circuit divided by the half power bandwidth Ø All inductors exhibit some extra resistance to ac or rf Ø Q is the reactance of the inductor divided by this ac or rf resistance § § − NMR probes Q > 300 Higher the probe Q the greater the sensitivity High Q for an NMR probe is required for high Signal-to-Noise § Sample can effect the Q of the probe Ø Ø The sample increases losses in the resonant circuit by inducing eddy currents in the solvent The more conductive the sample the more the losses and the lower the probe Q. – Water, high salt lower the Q of the probe – Lower Q longer pulse widths X – reactance of circuit in Ohms RL – the series resistance of the circuit in Ohms
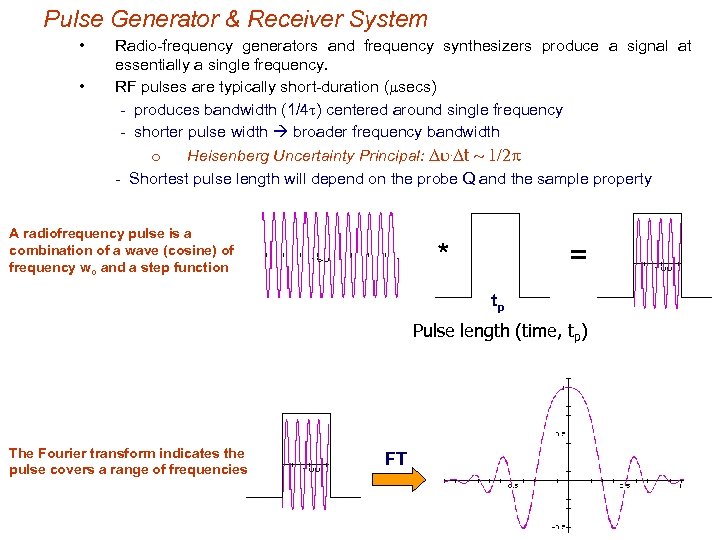
Pulse Generator & Receiver System • • Radio-frequency generators and frequency synthesizers produce a signal at essentially a single frequency. RF pulses are typically short-duration (msecs) - produces bandwidth (1/4 t) centered around single frequency - shorter pulse width broader frequency bandwidth o Heisenberg Uncertainty Principal: Du. Dt ~ 1/2 p - Shortest pulse length will depend on the probe Q and the sample property A radiofrequency pulse is a combination of a wave (cosine) of frequency wo and a step function * = tp Pulse length (time, tp) The Fourier transform indicates the pulse covers a range of frequencies FT
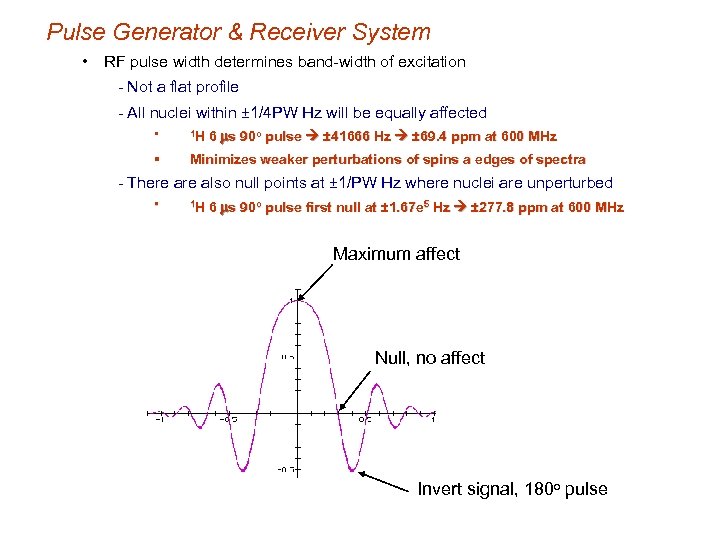
Pulse Generator & Receiver System • RF pulse width determines band-width of excitation - Not a flat profile - All nuclei within ± 1/4 PW Hz will be equally affected 6 ms 90 o pulse ± 41666 Hz ± 69. 4 ppm at 600 MHz § 1 H § Minimizes weaker perturbations of spins a edges of spectra - There also null points at ± 1/PW Hz where nuclei are unperturbed § 1 H 6 ms 90 o pulse first null at ± 1. 67 e 5 Hz ± 277. 8 ppm at 600 MHz Maximum affect Null, no affect Invert signal, 180 o pulse
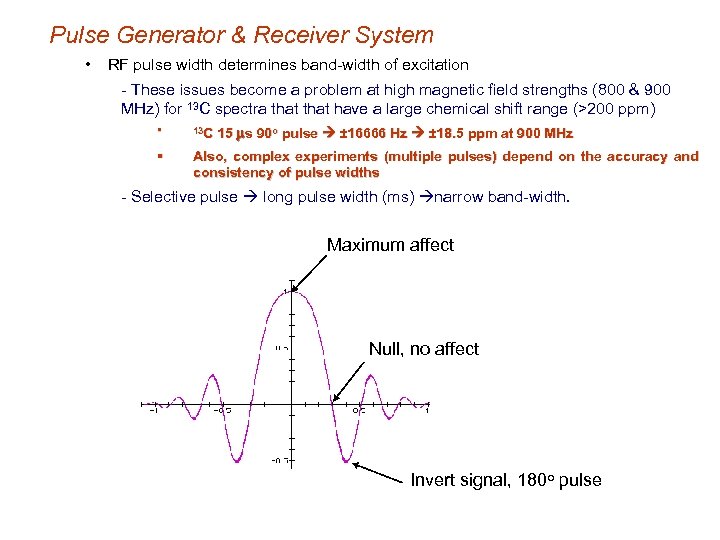
Pulse Generator & Receiver System • RF pulse width determines band-width of excitation - These issues become a problem at high magnetic field strengths (800 & 900 MHz) for 13 C spectra that have a large chemical shift range (>200 ppm) 15 ms 90 o pulse ± 16666 Hz ± 18. 5 ppm at 900 MHz § 13 C § Also, complex experiments (multiple pulses) depend on the accuracy and consistency of pulse widths - Selective pulse long pulse width (ms) narrow band-width. Maximum affect Null, no affect Invert signal, 180 o pulse
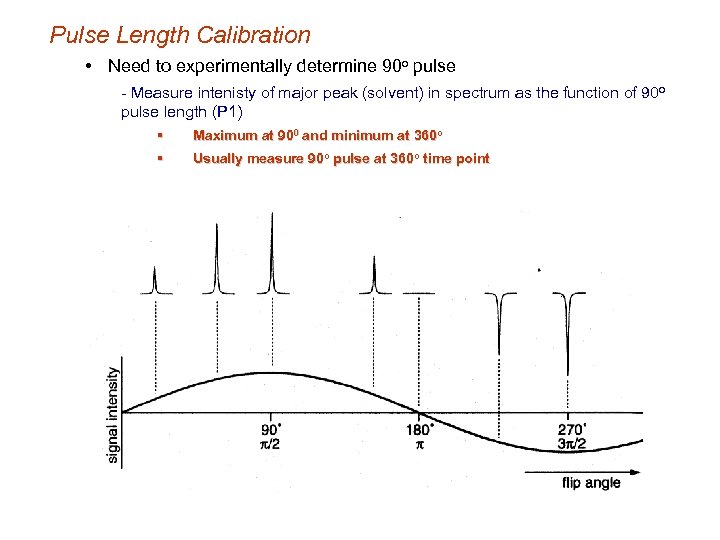
Pulse Length Calibration • Need to experimentally determine 90 o pulse - Measure intenisty of major peak (solvent) in spectrum as the function of 90 o pulse length (P 1) § Maximum at 900 and minimum at 360 o § Usually measure 90 o pulse at 360 o time point
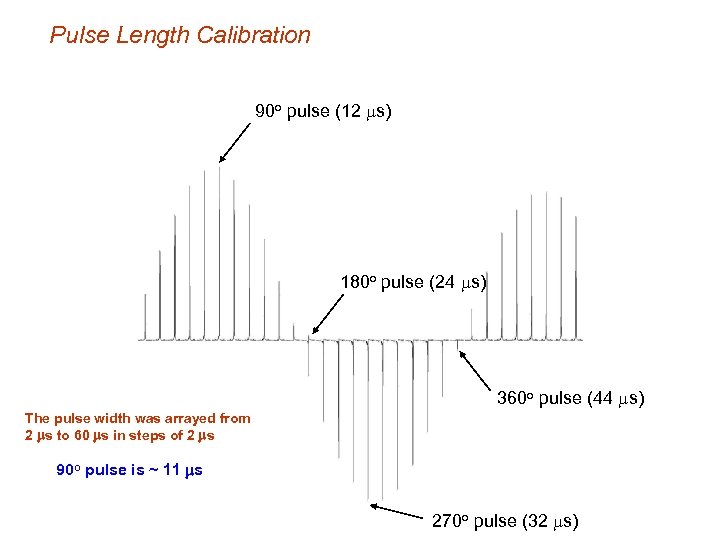
Pulse Length Calibration 90 o pulse (12 ms) 180 o pulse (24 ms) 360 o pulse (44 ms) The pulse width was arrayed from 2 ms to 60 ms in steps of 2 ms 90 o pulse is ~ 11 ms 270 o pulse (32 ms)
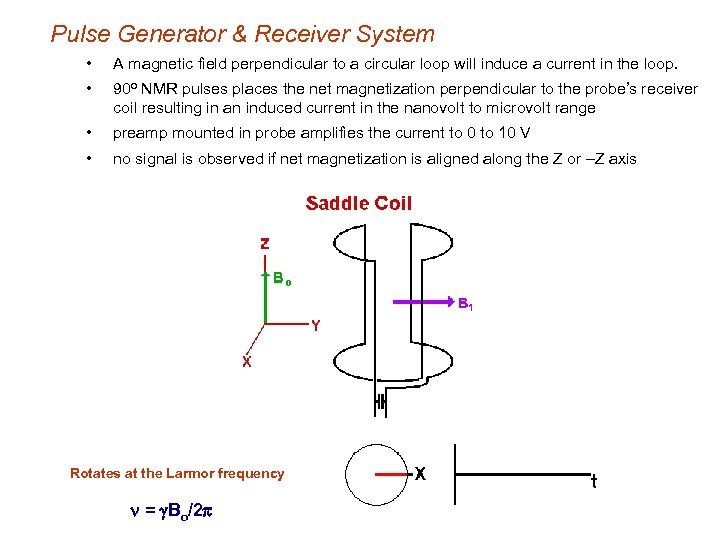
Pulse Generator & Receiver System • A magnetic field perpendicular to a circular loop will induce a current in the loop. • 90 o NMR pulses places the net magnetization perpendicular to the probe’s receiver coil resulting in an induced current in the nanovolt to microvolt range • preamp mounted in probe amplifies the current to 0 to 10 V • no signal is observed if net magnetization is aligned along the Z or –Z axis Rotates at the Larmor frequency n = g. Bo/2 p
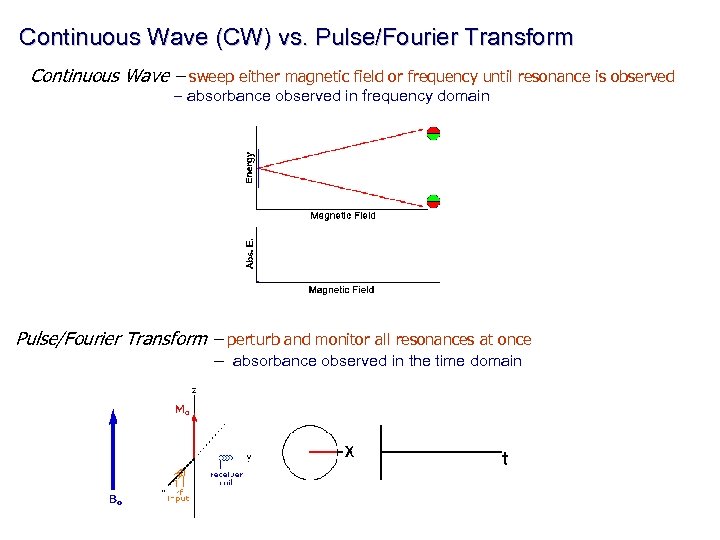
Continuous Wave (CW) vs. Pulse/Fourier Transform Continuous Wave – sweep either magnetic field or frequency until resonance is observed – absorbance observed in frequency domain Pulse/Fourier Transform – perturb and monitor all resonances at once – absorbance observed in the time domain
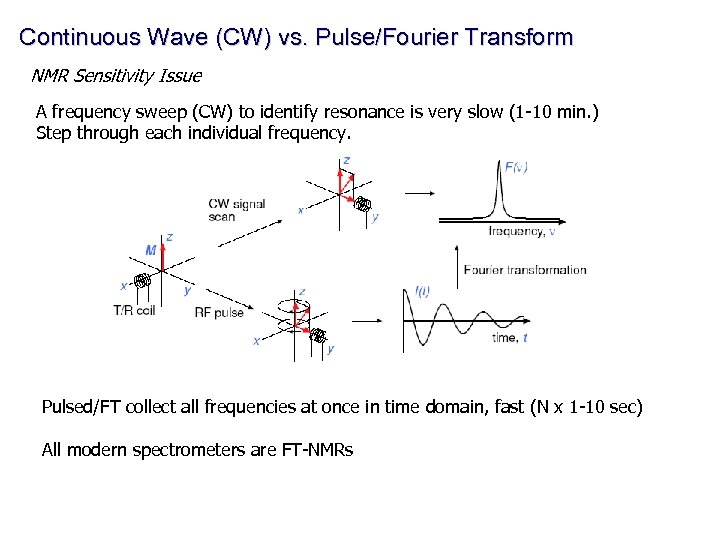
Continuous Wave (CW) vs. Pulse/Fourier Transform NMR Sensitivity Issue A frequency sweep (CW) to identify resonance is very slow (1 -10 min. ) Step through each individual frequency. Pulsed/FT collect all frequencies at once in time domain, fast (N x 1 -10 sec) All modern spectrometers are FT-NMRs
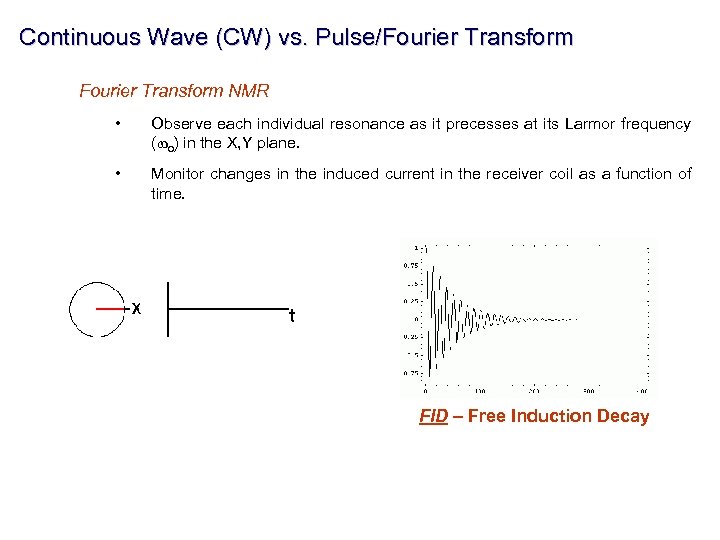
Continuous Wave (CW) vs. Pulse/Fourier Transform NMR • Observe each individual resonance as it precesses at its Larmor frequency (wo) in the X, Y plane. • Monitor changes in the induced current in the receiver coil as a function of time. FID – Free Induction Decay
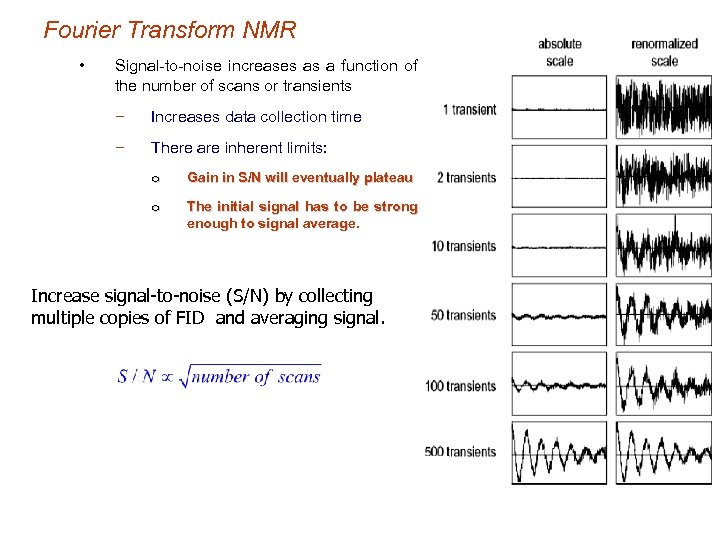
Fourier Transform NMR • Signal-to-noise increases as a function of the number of scans or transients − Increases data collection time − There are inherent limits: o Gain in S/N will eventually plateau o The initial signal has to be strong enough to signal average. Increase signal-to-noise (S/N) by collecting multiple copies of FID and averaging signal.
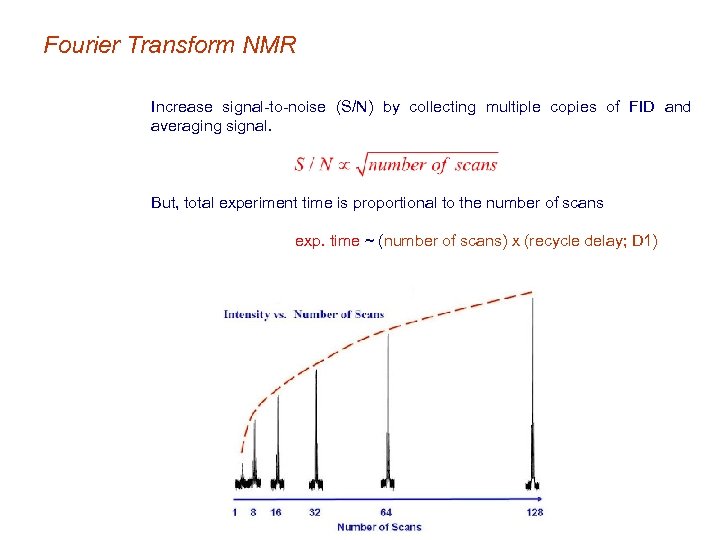
Fourier Transform NMR Increase signal-to-noise (S/N) by collecting multiple copies of FID and averaging signal. But, total experiment time is proportional to the number of scans exp. time ~ (number of scans) x (recycle delay; D 1)
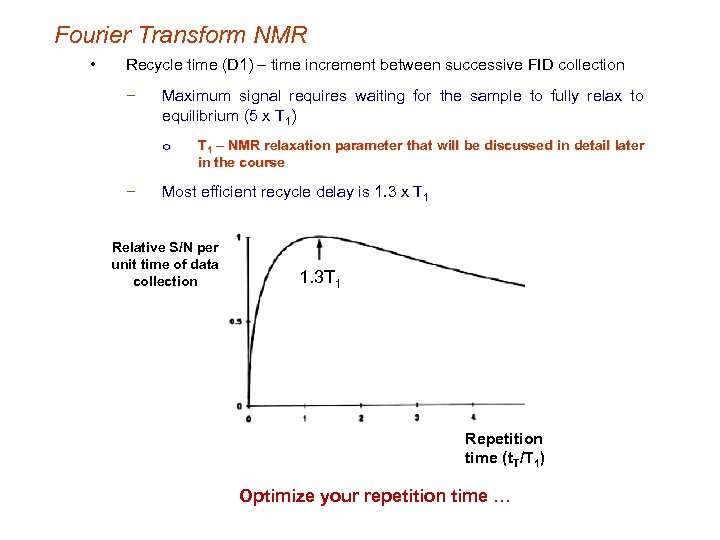
Fourier Transform NMR • Recycle time (D 1) – time increment between successive FID collection − Maximum signal requires waiting for the sample to fully relax to equilibrium (5 x T 1) o − T 1 – NMR relaxation parameter that will be discussed in detail later in the course Most efficient recycle delay is 1. 3 x T 1 Relative S/N per unit time of data collection 1. 3 T 1 Repetition time (t. T/T 1) Optimize your repetition time …
Fourier Transform NMR • Recycle time (D 1) – time increment between successive FID collection − Typical T 1’s for organic compounds range from 50 to 0. 5 seconds o T 1 relaxation times also vary by nuclei, where 13 C > 1 H o Either estimates from related compounds or experimental measurements of T 1 is required to optimize data collection especially for long data acquisitions.
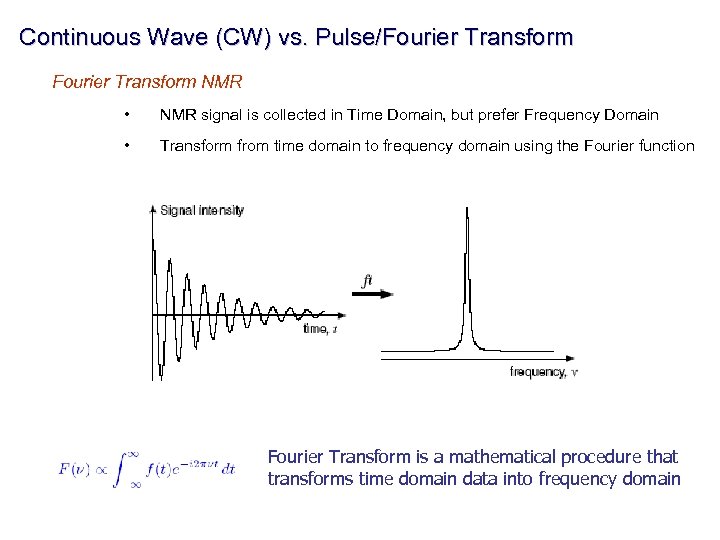
Continuous Wave (CW) vs. Pulse/Fourier Transform NMR • NMR signal is collected in Time Domain, but prefer Frequency Domain • Transform from time domain to frequency domain using the Fourier function Fourier Transform is a mathematical procedure that transforms time domain data into frequency domain
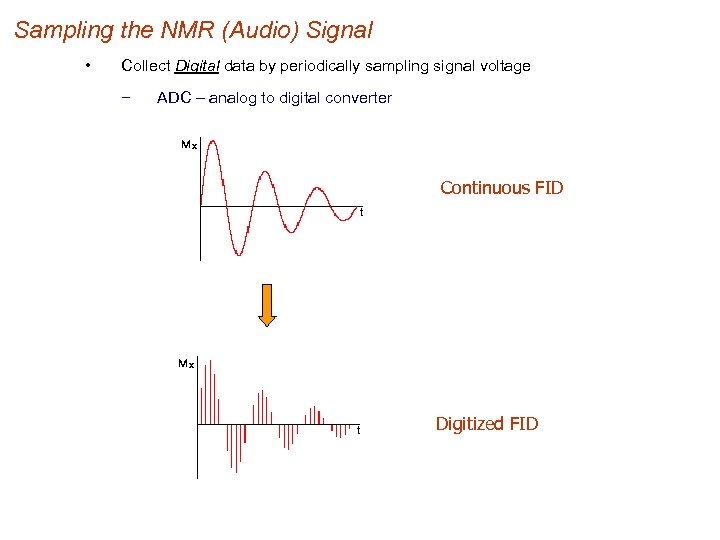
Sampling the NMR (Audio) Signal • Collect Digital data by periodically sampling signal voltage − ADC – analog to digital converter Continuous FID Digitized FID
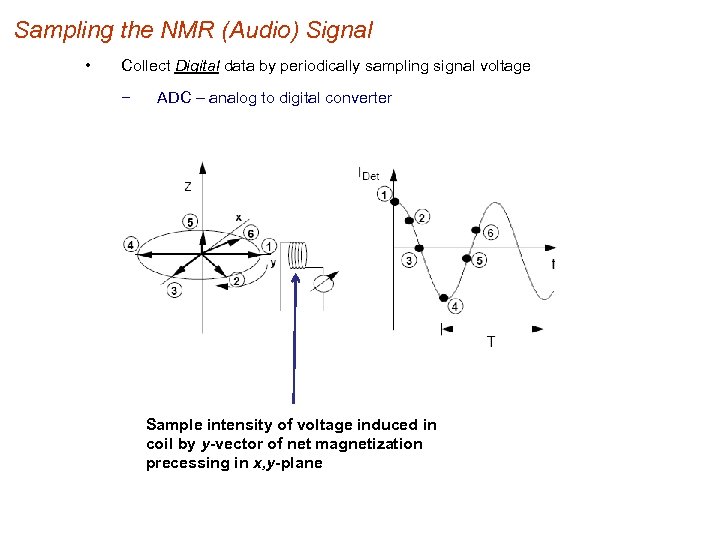
Sampling the NMR (Audio) Signal • Collect Digital data by periodically sampling signal voltage − ADC – analog to digital converter Sample intensity of voltage induced in coil by y-vector of net magnetization precessing in x, y-plane
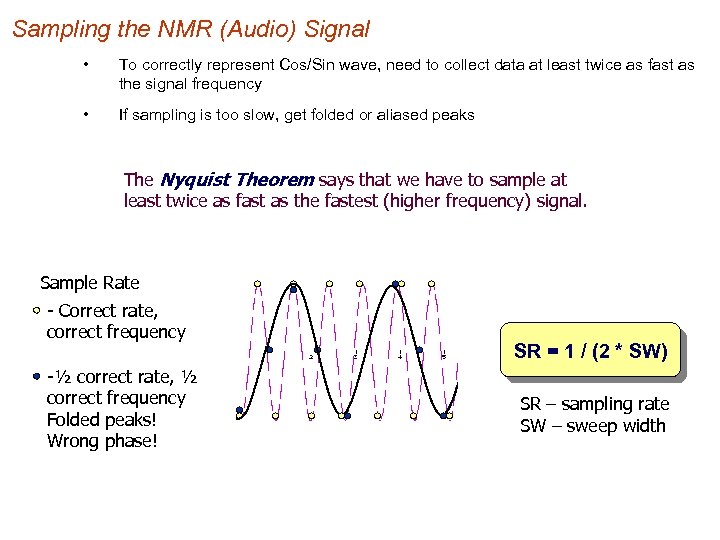
Sampling the NMR (Audio) Signal • To correctly represent Cos/Sin wave, need to collect data at least twice as fast as the signal frequency • If sampling is too slow, get folded or aliased peaks The Nyquist Theorem says that we have to sample at least twice as fast as the fastest (higher frequency) signal. Sample Rate - Correct rate, correct frequency -½ correct rate, ½ correct frequency Folded peaks! Wrong phase! SR = 1 / (2 * SW) SR – sampling rate SW – sweep width
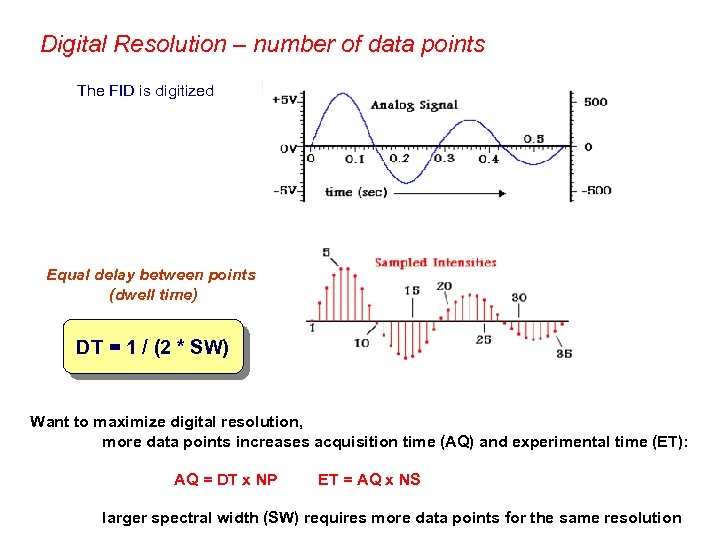
Digital Resolution – number of data points The FID is digitized Equal delay between points (dwell time) DT = 1 / (2 * SW) Want to maximize digital resolution, more data points increases acquisition time (AQ) and experimental time (ET): AQ = DT x NP ET = AQ x NS larger spectral width (SW) requires more data points for the same resolution
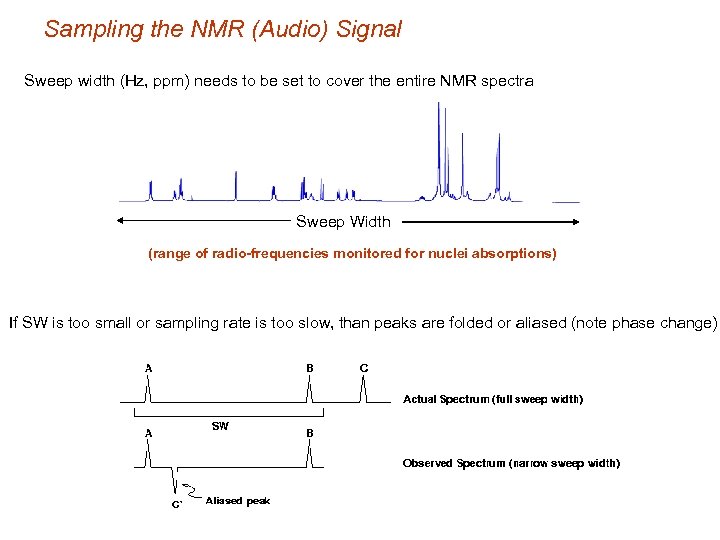
Sampling the NMR (Audio) Signal Sweep width (Hz, ppm) needs to be set to cover the entire NMR spectra Sweep Width (range of radio-frequencies monitored for nuclei absorptions) If SW is too small or sampling rate is too slow, than peaks are folded or aliased (note phase change)
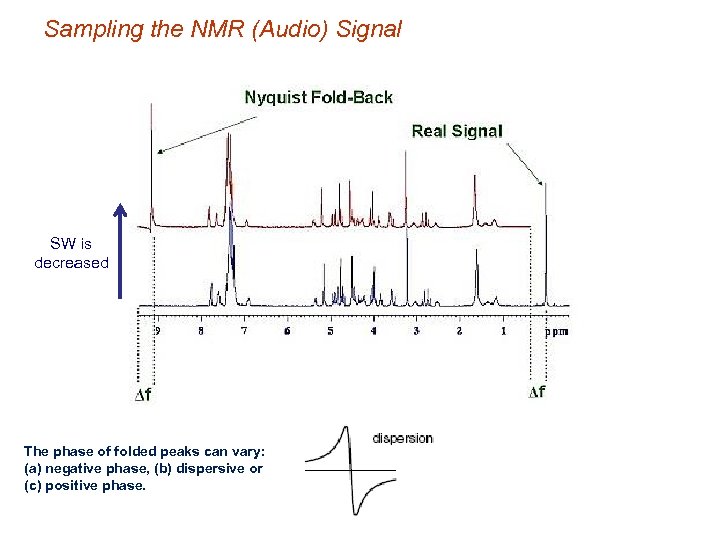
Sampling the NMR (Audio) Signal SW is decreased The phase of folded peaks can vary: (a) negative phase, (b) dispersive or (c) positive phase.
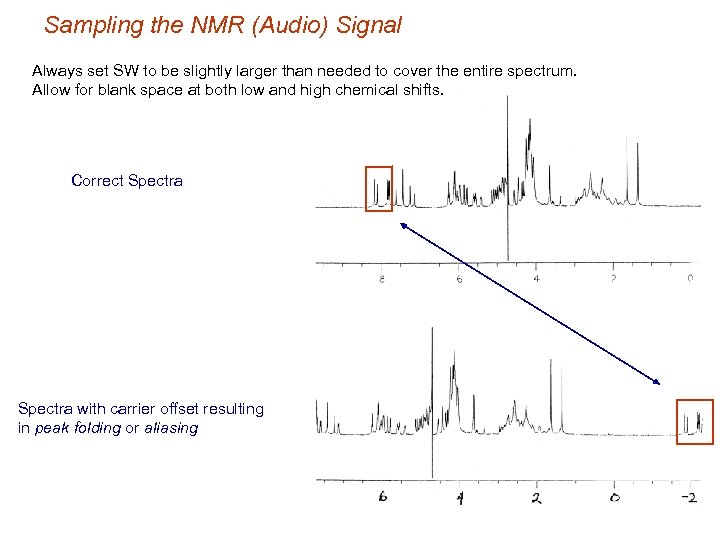
Sampling the NMR (Audio) Signal Always set SW to be slightly larger than needed to cover the entire spectrum. Allow for blank space at both low and high chemical shifts. Correct Spectra with carrier offset resulting in peak folding or aliasing

Sampling the NMR (Audio) Signal NMR data size • Analog signal is digitized by periodically monitoring the induced current in the receiver coil • How many data points are collected? • What is the time delay between data points? • How long do you sample for? − Sample too long collecting noise & wasting time All this noise added to spectra Higher Digital Resolution requires longer acquisition times
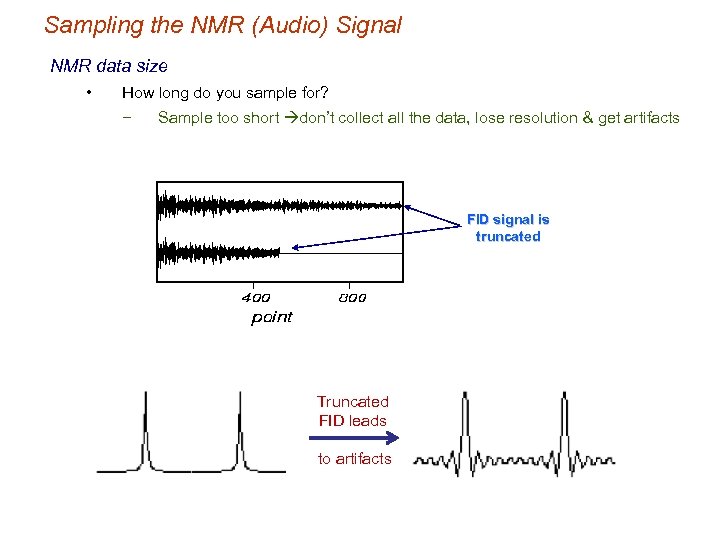
Sampling the NMR (Audio) Signal NMR data size • How long do you sample for? − Sample too short don’t collect all the data, lose resolution & get artifacts FID signal is truncated Truncated FID leads to artifacts
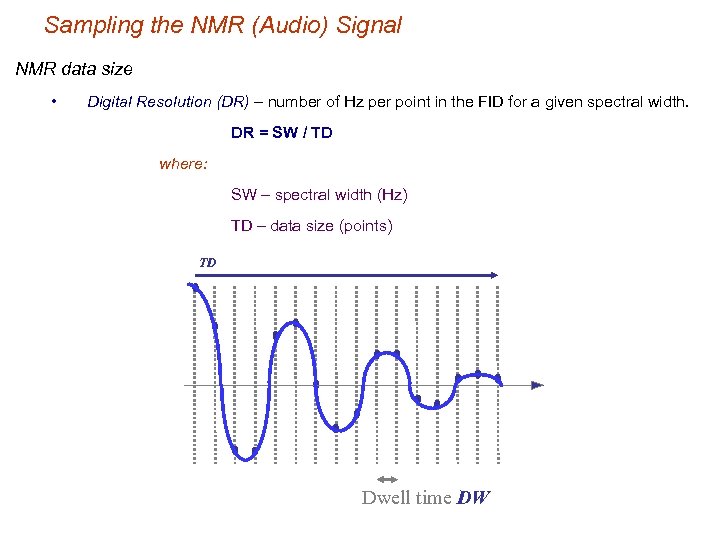
Sampling the NMR (Audio) Signal NMR data size • Digital Resolution (DR) – number of Hz per point in the FID for a given spectral width. DR = SW / TD where: SW – spectral width (Hz) TD – data size (points) TD Dwell time DW
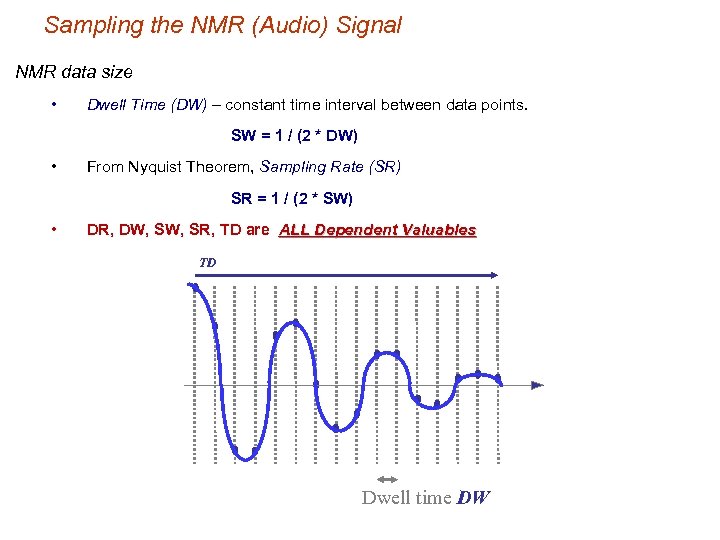
Sampling the NMR (Audio) Signal NMR data size • Dwell Time (DW) – constant time interval between data points. SW = 1 / (2 * DW) • From Nyquist Theorem, Sampling Rate (SR) SR = 1 / (2 * SW) • DR, DW, SR, TD are ALL Dependent Valuables TD Dwell time DW
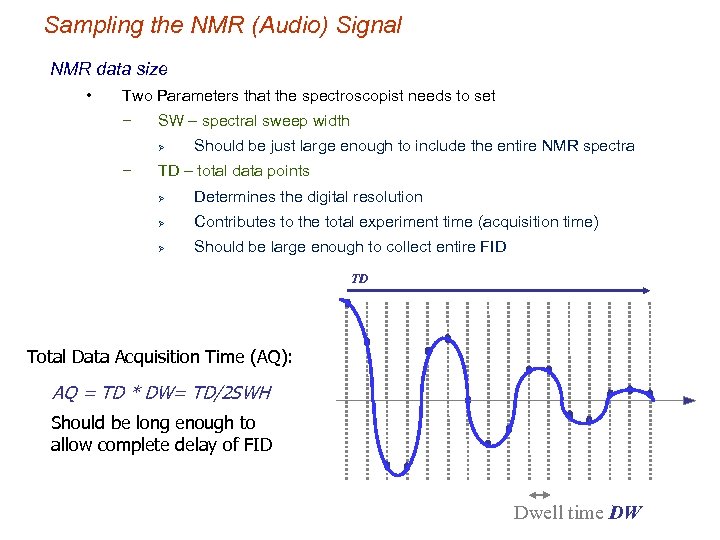
Sampling the NMR (Audio) Signal NMR data size • Two Parameters that the spectroscopist needs to set − SW – spectral sweep width Ø − Should be just large enough to include the entire NMR spectra TD – total data points Ø Determines the digital resolution Ø Contributes to the total experiment time (acquisition time) Ø Should be large enough to collect entire FID TD Total Data Acquisition Time (AQ): AQ = TD * DW= TD/2 SWH Should be long enough to allow complete delay of FID Dwell time DW
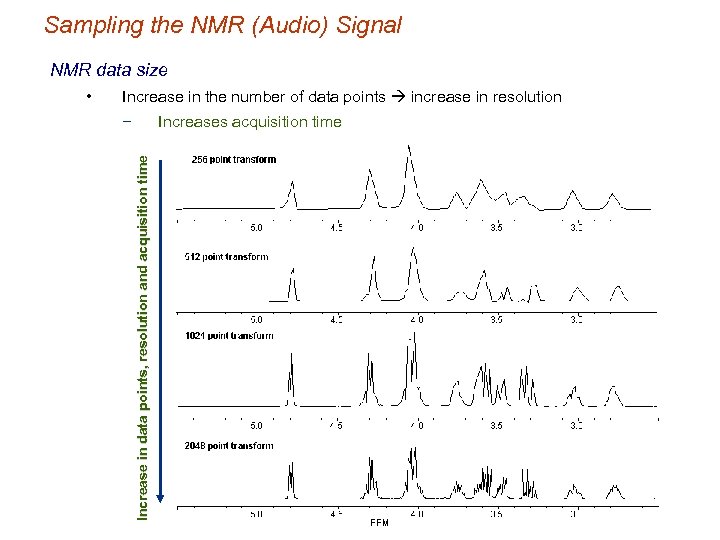
Sampling the NMR (Audio) Signal NMR data size Increase in the number of data points increase in resolution − Increases acquisition time Increase in data points, resolution and acquisition time •
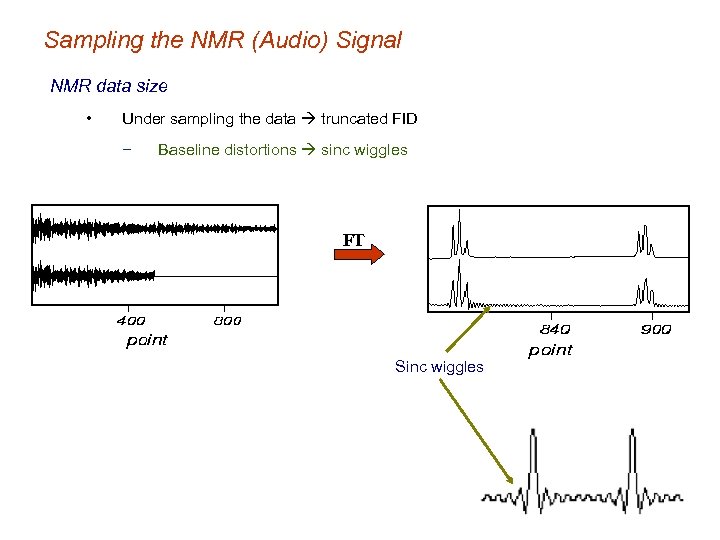
Sampling the NMR (Audio) Signal NMR data size • Under sampling the data truncated FID − Baseline distortions sinc wiggles FT Sinc wiggles
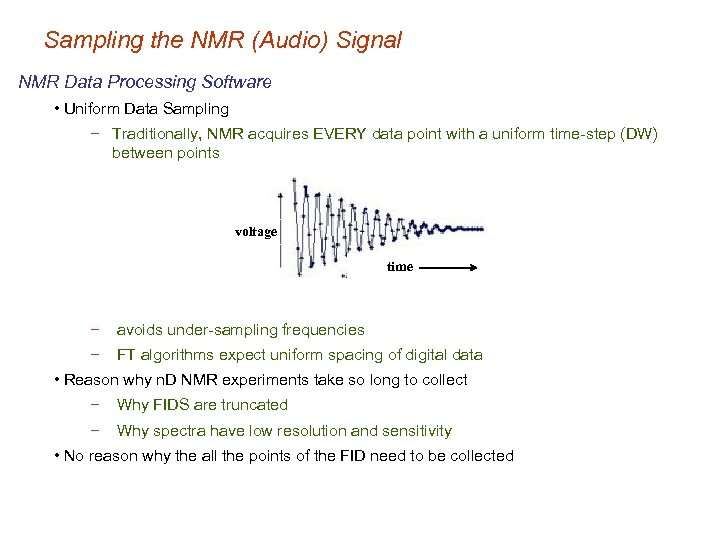
Sampling the NMR (Audio) Signal NMR Data Processing Software • Uniform Data Sampling − Traditionally, NMR acquires EVERY data point with a uniform time-step (DW) between points voltage time − avoids under-sampling frequencies − FT algorithms expect uniform spacing of digital data • Reason why n. D NMR experiments take so long to collect − Why FIDS are truncated − Why spectra have low resolution and sensitivity • No reason why the all the points of the FID need to be collected
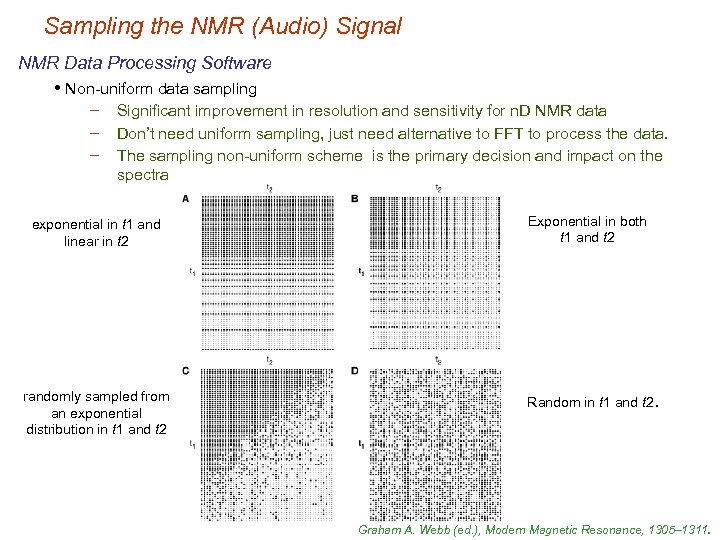
Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − − − Significant improvement in resolution and sensitivity for n. D NMR data Don’t need uniform sampling, just need alternative to FFT to process the data. The sampling non-uniform scheme is the primary decision and impact on the spectra exponential in t 1 and linear in t 2 randomly sampled from an exponential distribution in t 1 and t 2 Exponential in both t 1 and t 2 Random in t 1 and t 2. Graham A. Webb (ed. ), Modern Magnetic Resonance, 1305– 1311.
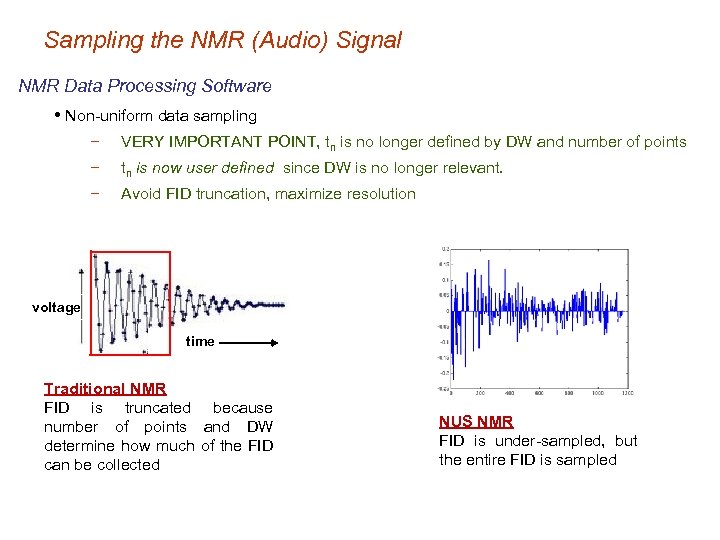
Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − VERY IMPORTANT POINT, tn is no longer defined by DW and number of points − tn is now user defined since DW is no longer relevant. − Avoid FID truncation, maximize resolution voltage time Traditional NMR FID is truncated because number of points and DW determine how much of the FID can be collected NUS NMR FID is under-sampled, but the entire FID is sampled
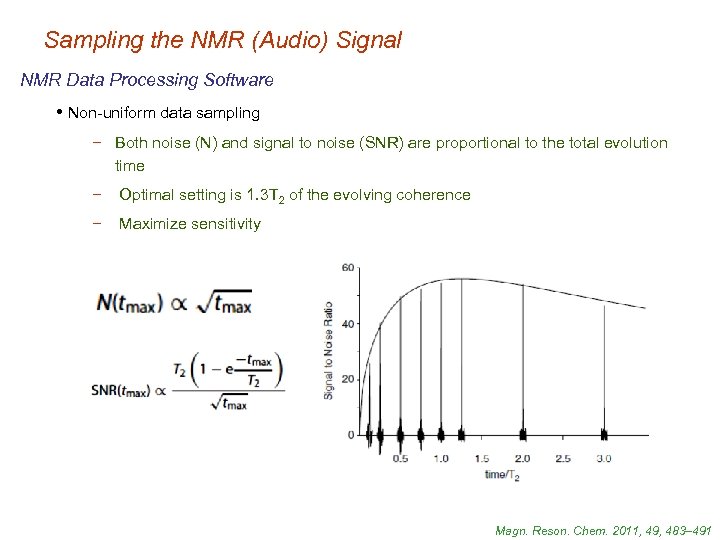
Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − Both noise (N) and signal to noise (SNR) are proportional to the total evolution time − Optimal setting is 1. 3 T 2 of the evolving coherence − Maximize sensitivity Magn. Reson. Chem. 2011, 49, 483– 491

Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − What is the optimal sampling density? − Increase enhancement by increase exponential bias, eventually regenerate truncated FID − Highly resolved spectra is p. T 2 TSMP – time constant for the exponential weighting of the sampling. h – enhancement lw – line width Magn. Reson. Chem. 2011, 49, 483– 491
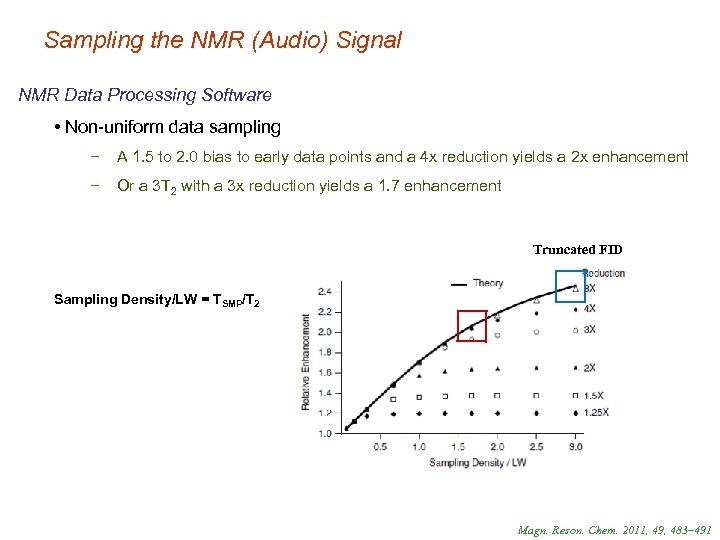
Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − A 1. 5 to 2. 0 bias to early data points and a 4 x reduction yields a 2 x enhancement − Or a 3 T 2 with a 3 x reduction yields a 1. 7 enhancement Truncated FID Sampling Density/LW = TSMP/T 2 Magn. Reson. Chem. 2011, 49, 483– 491
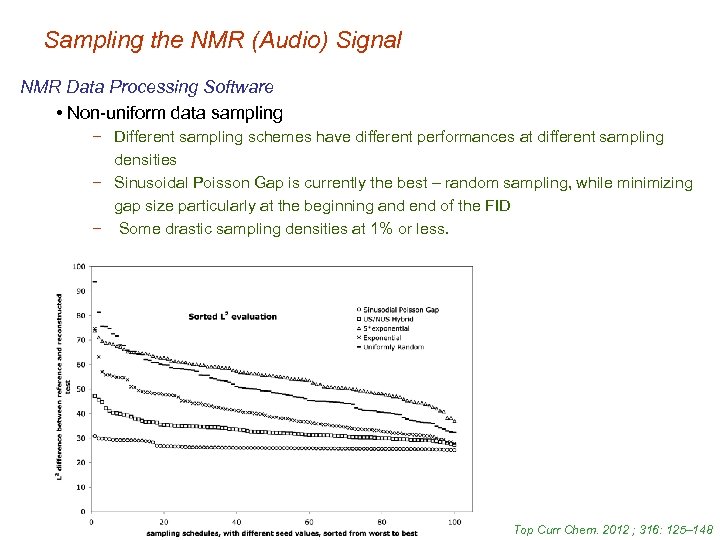
Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − Different sampling schemes have different performances at different sampling densities − Sinusoidal Poisson Gap is currently the best – random sampling, while minimizing gap size particularly at the beginning and end of the FID − Some drastic sampling densities at 1% or less. Top Curr Chem. 2012 ; 316: 125– 148
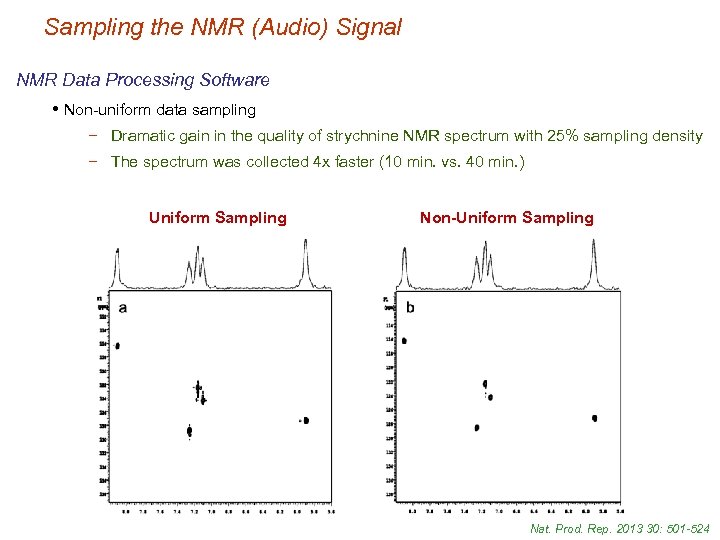
Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − Dramatic gain in the quality of strychnine NMR spectrum with 25% sampling density − The spectrum was collected 4 x faster (10 min. vs. 40 min. ) Uniform Sampling Non-Uniform Sampling Nat. Prod. Rep. 2013 30: 501 -524

Sampling the NMR (Audio) Signal NMR Data Processing Software • Non-uniform data sampling − How is the time-domain data processed? − Use the partial data to reconstruct the full Nyquist grid then process as normal Ø maximum entropy reconstruction is a common approach Ø forward maximum entropy (FM), fast maximum likelihood reconstruction (FMLR) Ø multi-dimensional decomposition (MDD); and compressed sensing (CS) − Mdd. NMR: http: //www. enmr. eu/webportal/mdd. html − Newton: http: //newton. nmrfam. wisc. edu/newton/static_web/index. html − RNMRTK: http: //rnmrtk. uchc. edu/rnmrtk/RNMRTK. html − mpi. Pipe: Available by contacting the Wagner Group
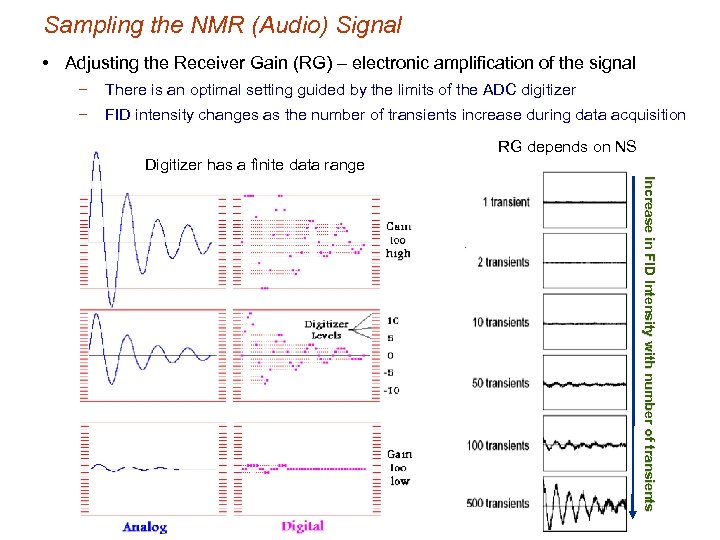
Sampling the NMR (Audio) Signal • Adjusting the Receiver Gain (RG) – electronic amplification of the signal − There is an optimal setting guided by the limits of the ADC digitizer − FID intensity changes as the number of transients increase during data acquisition RG depends on NS Digitizer has a finite data range Increase in FID Intensity with number of transients
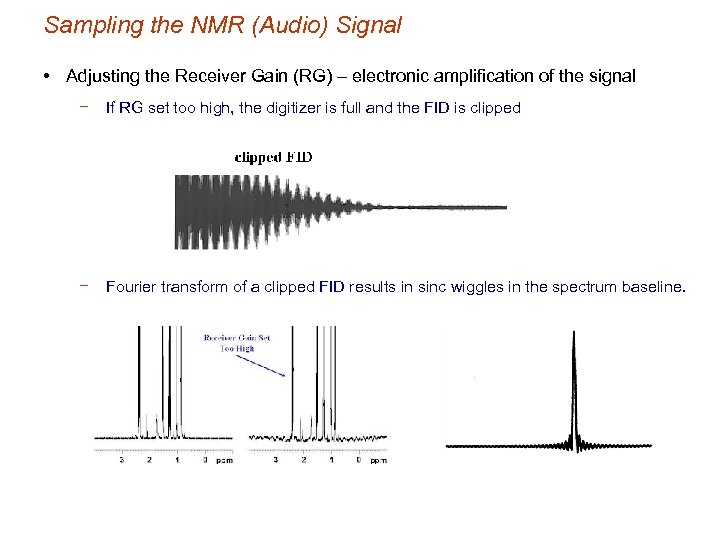
Sampling the NMR (Audio) Signal • Adjusting the Receiver Gain (RG) – electronic amplification of the signal − If RG set too high, the digitizer is full and the FID is clipped − Fourier transform of a clipped FID results in sinc wiggles in the spectrum baseline.
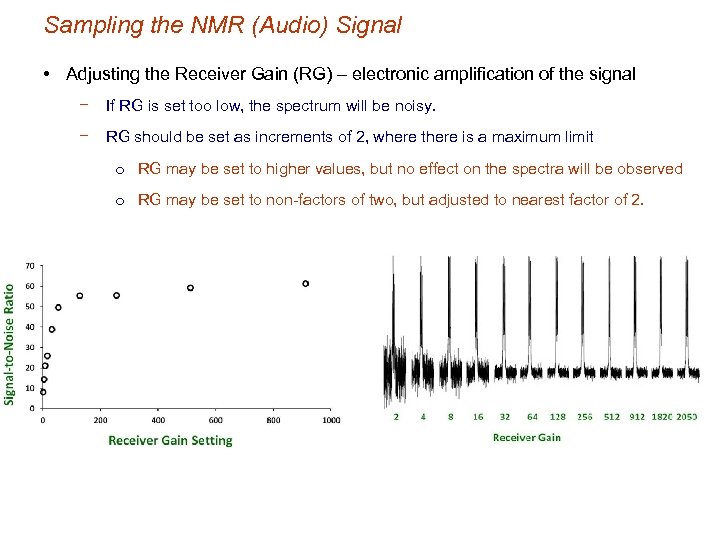
Sampling the NMR (Audio) Signal • Adjusting the Receiver Gain (RG) – electronic amplification of the signal − If RG is set too low, the spectrum will be noisy. − RG should be set as increments of 2, where there is a maximum limit o RG may be set to higher values, but no effect on the spectra will be observed o RG may be set to non-factors of two, but adjusted to nearest factor of 2.
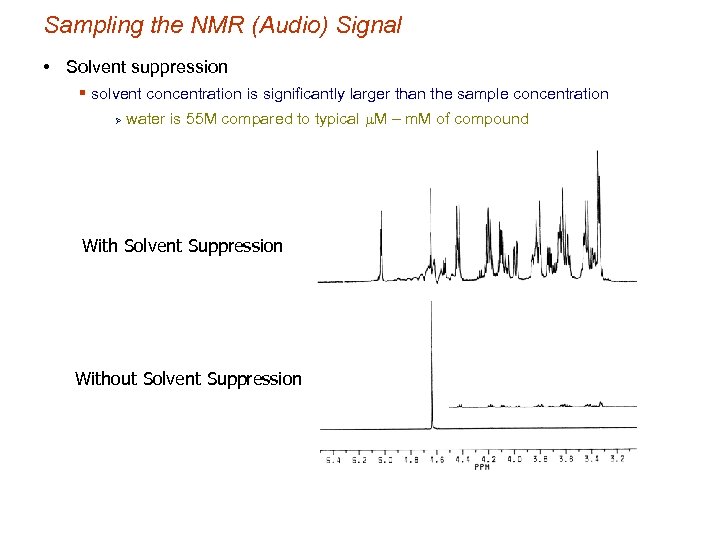
Sampling the NMR (Audio) Signal • Solvent suppression § solvent concentration is significantly larger than the sample concentration Ø water is 55 M compared to typical m. M – m. M of compound With Solvent Suppression Without Solvent Suppression
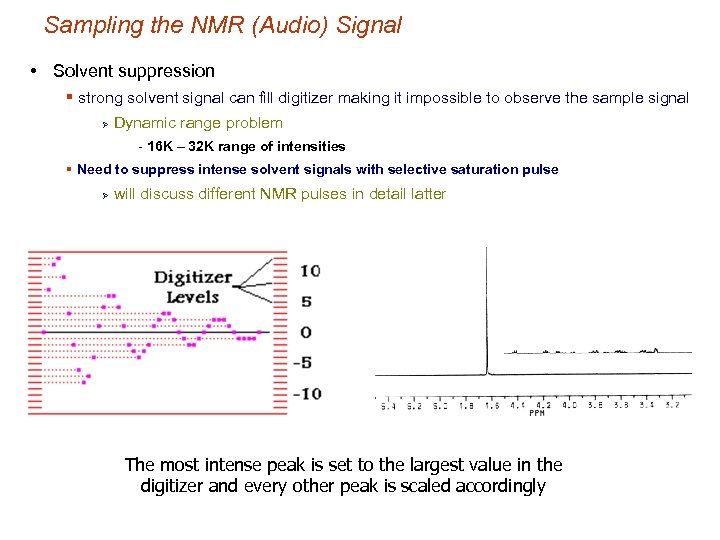
Sampling the NMR (Audio) Signal • Solvent suppression § strong solvent signal can fill digitizer making it impossible to observe the sample signal Ø Dynamic range problem - 16 K – 32 K range of intensities § Need to suppress intense solvent signals with selective saturation pulse Ø will discuss different NMR pulses in detail latter The most intense peak is set to the largest value in the digitizer and every other peak is scaled accordingly
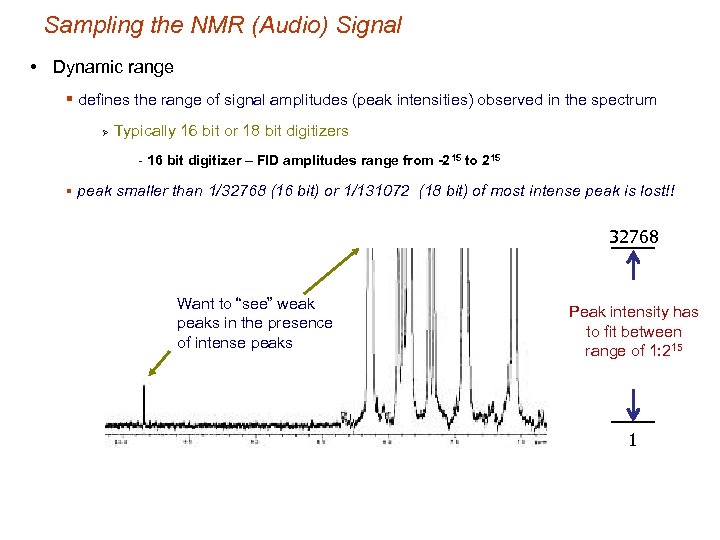
Sampling the NMR (Audio) Signal • Dynamic range § defines the range of signal amplitudes (peak intensities) observed in the spectrum Ø Typically 16 bit or 18 bit digitizers - 16 bit digitizer – FID amplitudes range from -215 to 215 § peak smaller than 1/32768 (16 bit) or 1/131072 (18 bit) of most intense peak is lost!! 32768 Want to “see” weak peaks in the presence of intense peaks Peak intensity has to fit between range of 1: 215 1
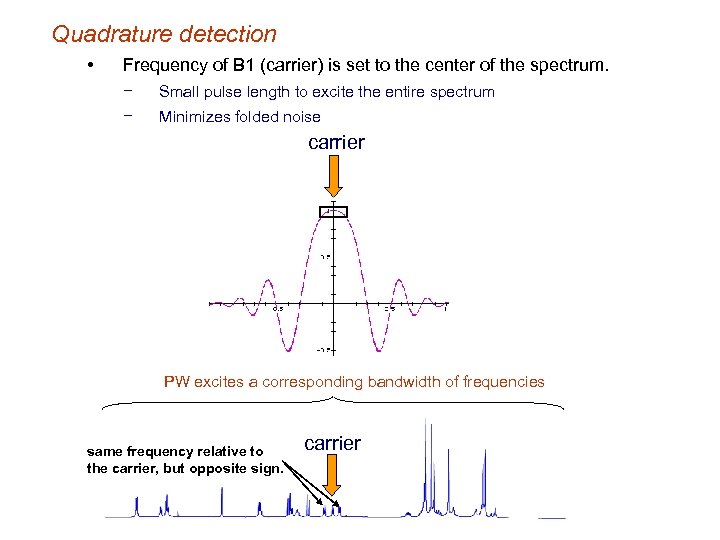
Quadrature detection • Frequency of B 1 (carrier) is set to the center of the spectrum. − Small pulse length to excite the entire spectrum − Minimizes folded noise carrier PW excites a corresponding bandwidth of frequencies same frequency relative to the carrier, but opposite sign. carrier
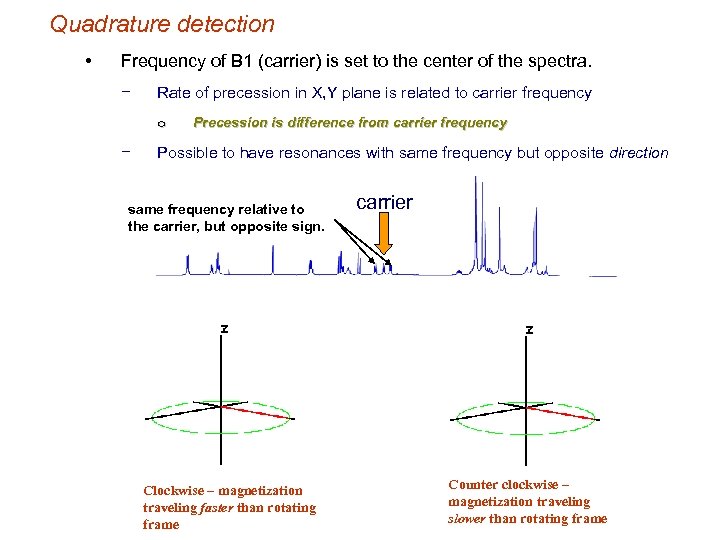
Quadrature detection • Frequency of B 1 (carrier) is set to the center of the spectra. − Rate of precession in X, Y plane is related to carrier frequency o − Precession is difference from carrier frequency Possible to have resonances with same frequency but opposite direction same frequency relative to the carrier, but opposite sign. Clockwise – magnetization traveling faster than rotating frame carrier Counter clockwise – magnetization traveling slower than rotating frame
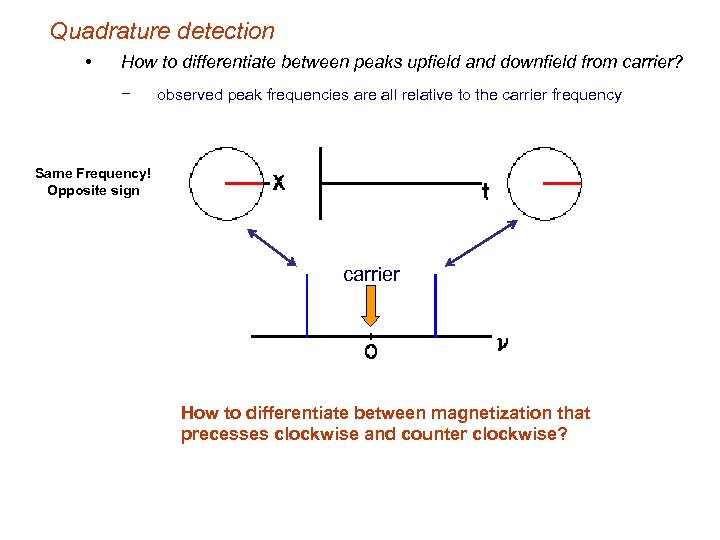
Quadrature detection • How to differentiate between peaks upfield and downfield from carrier? − observed peak frequencies are all relative to the carrier frequency Same Frequency! Opposite sign carrier How to differentiate between magnetization that precesses clockwise and counter clockwise?
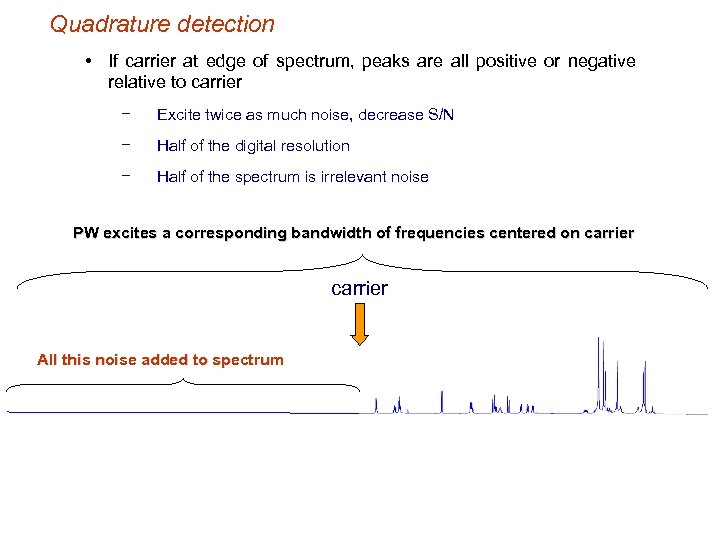
Quadrature detection • If carrier at edge of spectrum, peaks are all positive or negative relative to carrier − Excite twice as much noise, decrease S/N − Half of the digital resolution − Half of the spectrum is irrelevant noise PW excites a corresponding bandwidth of frequencies centered on carrier All this noise added to spectrum
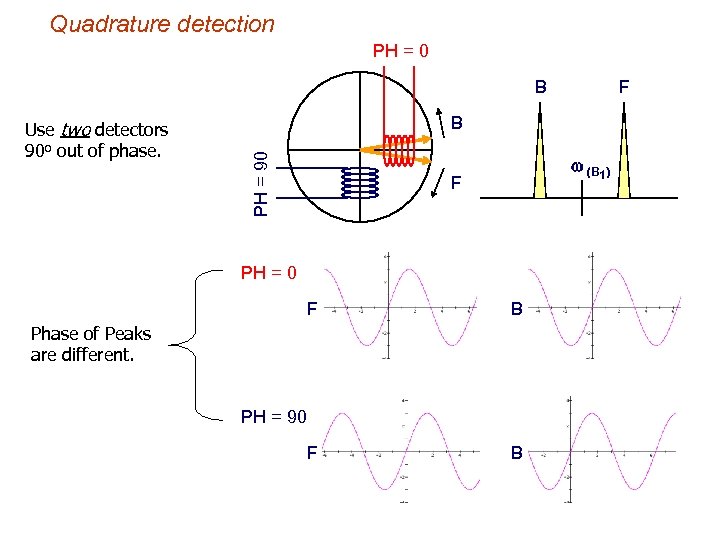
Quadrature detection PH = 0 B B PH = 90 Use two detectors 90 o out of phase. F w (B 1) F PH = 0 F B Phase of Peaks are different. PH = 90
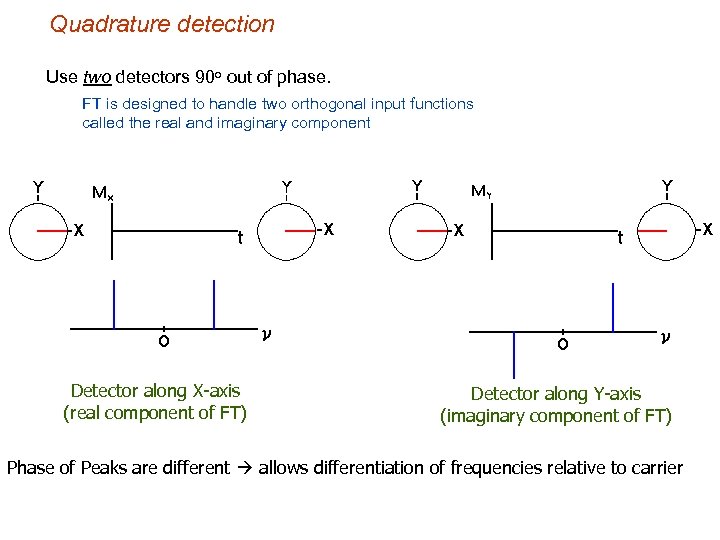
Quadrature detection Use two detectors 90 o out of phase. FT is designed to handle two orthogonal input functions called the real and imaginary component Detector along X-axis (real component of FT) Detector along Y-axis (imaginary component of FT) Phase of Peaks are different allows differentiation of frequencies relative to carrier
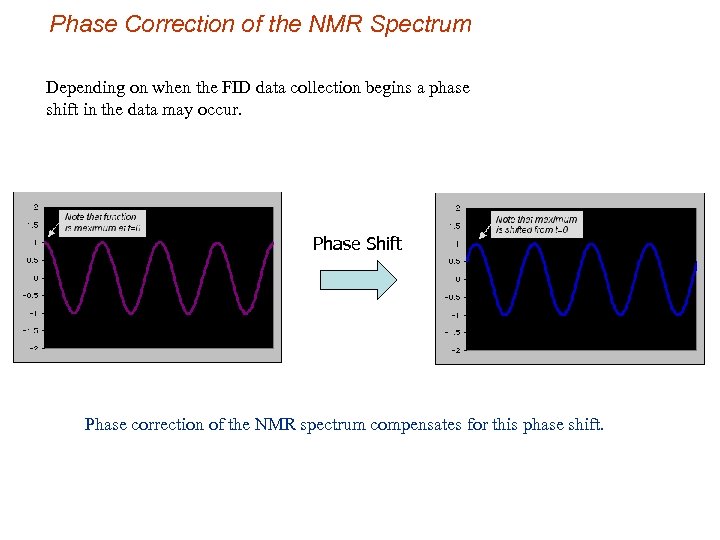
Phase Correction of the NMR Spectrum Depending on when the FID data collection begins a phase shift in the data may occur. Phase Shift Phase correction of the NMR spectrum compensates for this phase shift.
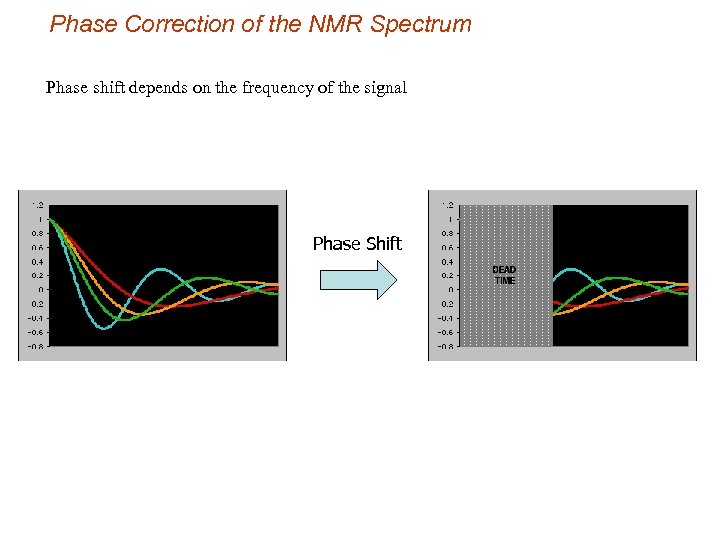
Phase Correction of the NMR Spectrum Phase shift depends on the frequency of the signal Phase Shift
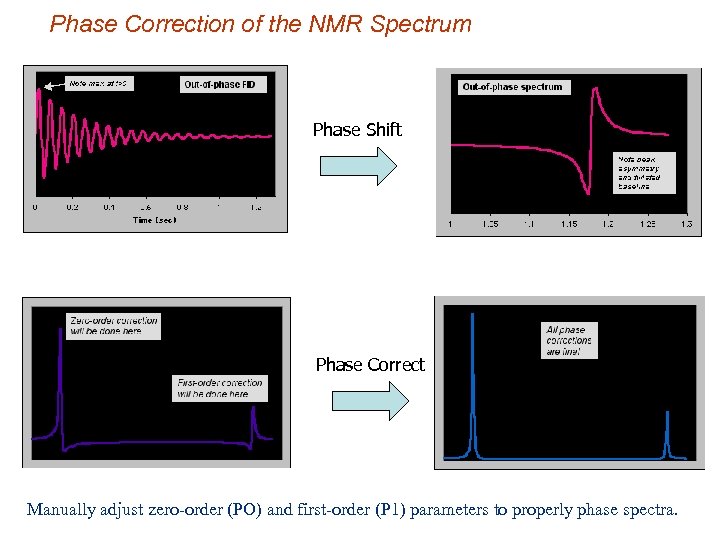
Phase Correction of the NMR Spectrum Phase Shift Phase Correct Manually adjust zero-order (PO) and first-order (P 1) parameters to properly phase spectra.
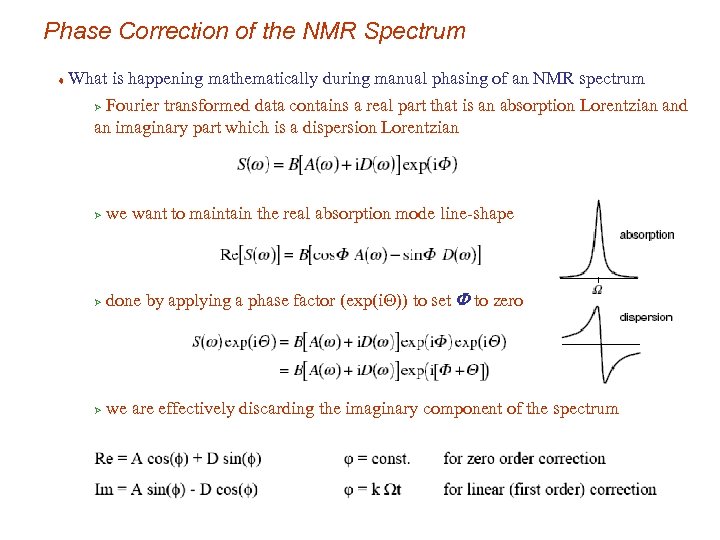
Phase Correction of the NMR Spectrum t What is happening mathematically during manual phasing of an NMR spectrum Fourier transformed data contains a real part that is an absorption Lorentzian and an imaginary part which is a dispersion Lorentzian Ø Ø we want to maintain the real absorption mode line-shape Ø done by applying a phase factor (exp(i. Q)) to set F to zero Ø we are effectively discarding the imaginary component of the spectrum
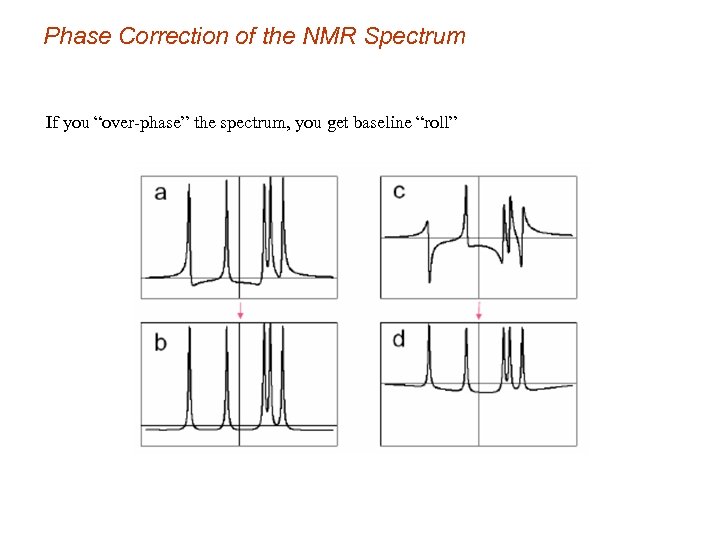
Phase Correction of the NMR Spectrum If you “over-phase” the spectrum, you get baseline “roll”
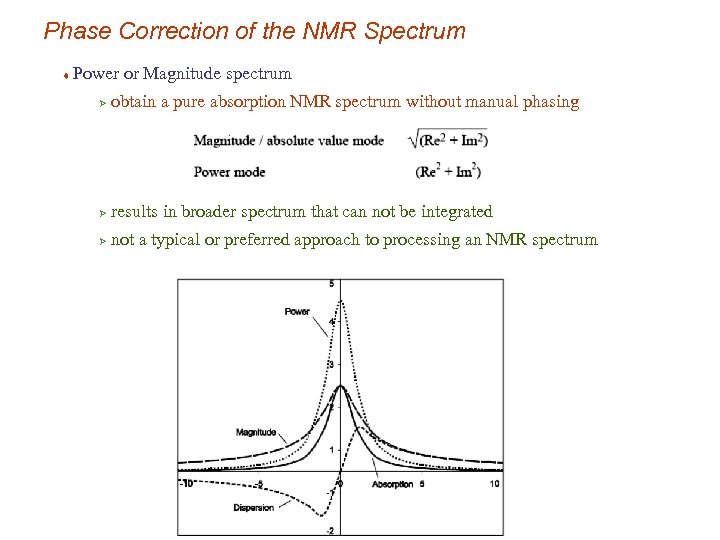
Phase Correction of the NMR Spectrum t Power or Magnitude spectrum Ø obtain a pure absorption NMR spectrum without manual phasing Ø results in broader spectrum that can not be integrated Ø not a typical or preferred approach to processing an NMR spectrum
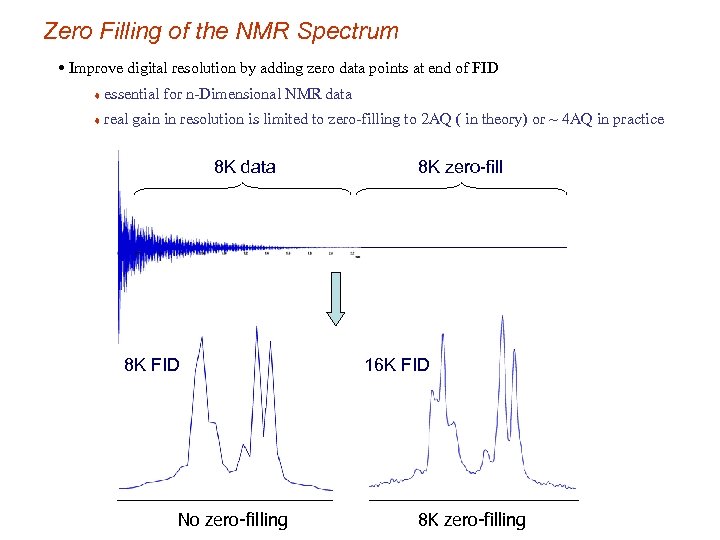
Zero Filling of the NMR Spectrum • Improve digital resolution by adding zero data points at end of FID t essential for n-Dimensional NMR data t real gain in resolution is limited to zero-filling to 2 AQ ( in theory) or ~ 4 AQ in practice 8 K data 8 K FID No zero-filling 8 K zero-fill 16 K FID 8 K zero-filling
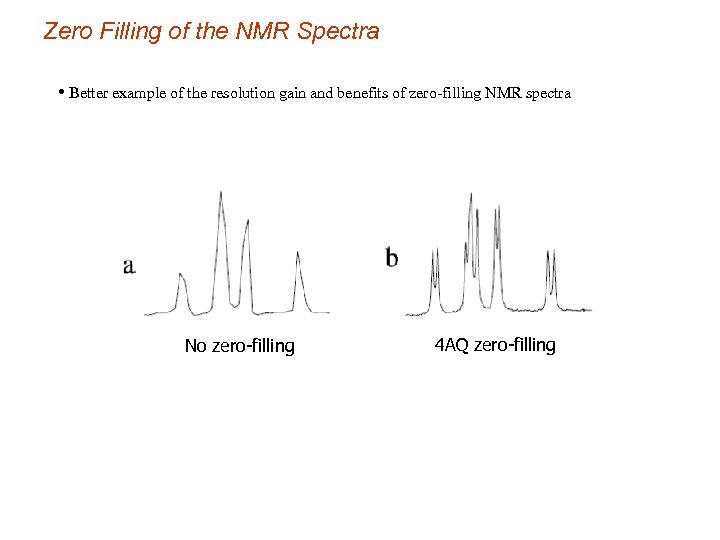
Zero Filling of the NMR Spectra • Better example of the resolution gain and benefits of zero-filling NMR spectra No zero-filling 4 AQ zero-filling
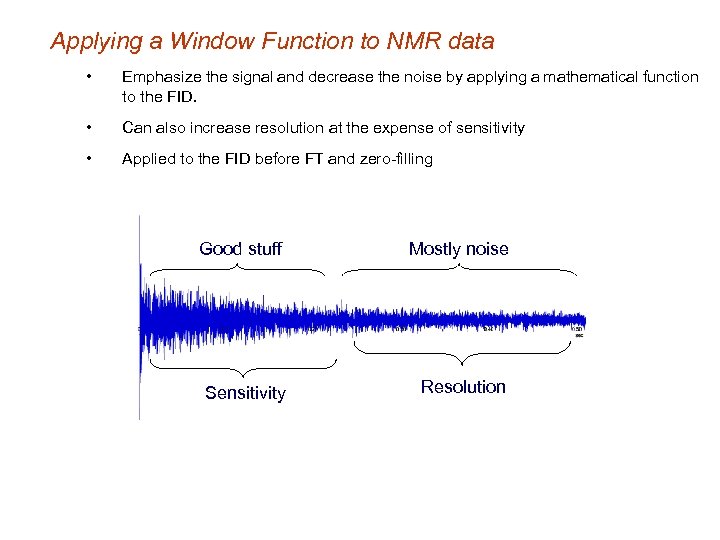
Applying a Window Function to NMR data • Emphasize the signal and decrease the noise by applying a mathematical function to the FID. • Can also increase resolution at the expense of sensitivity • Applied to the FID before FT and zero-filling Good stuff Mostly noise Sensitivity Resolution
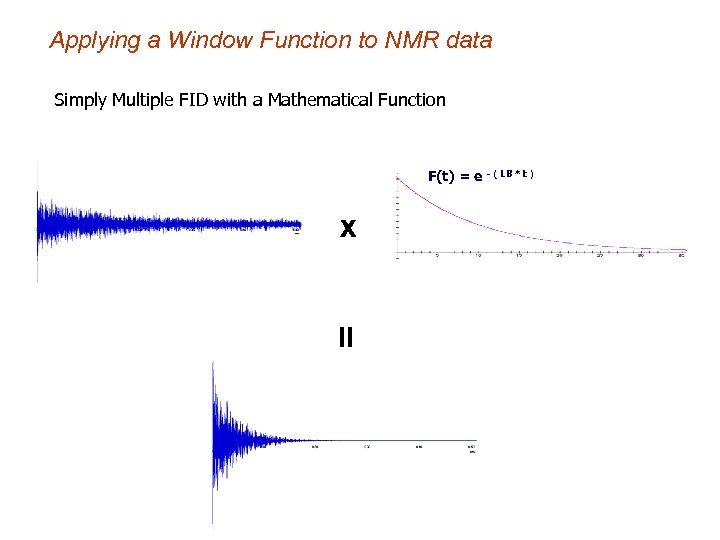
Applying a Window Function to NMR data Simply Multiple FID with a Mathematical Function F(t) = e - ( LB * t ) X =
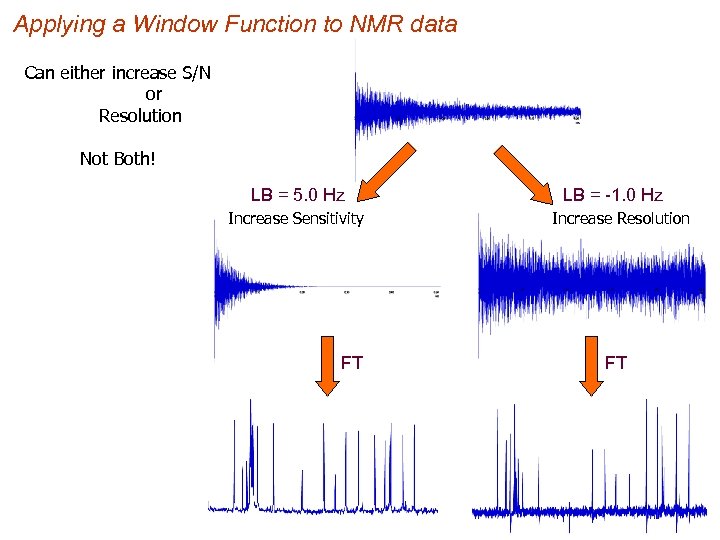
Applying a Window Function to NMR data Can either increase S/N or Resolution Not Both! LB = 5. 0 Hz Increase Sensitivity FT LB = -1. 0 Hz Increase Resolution FT
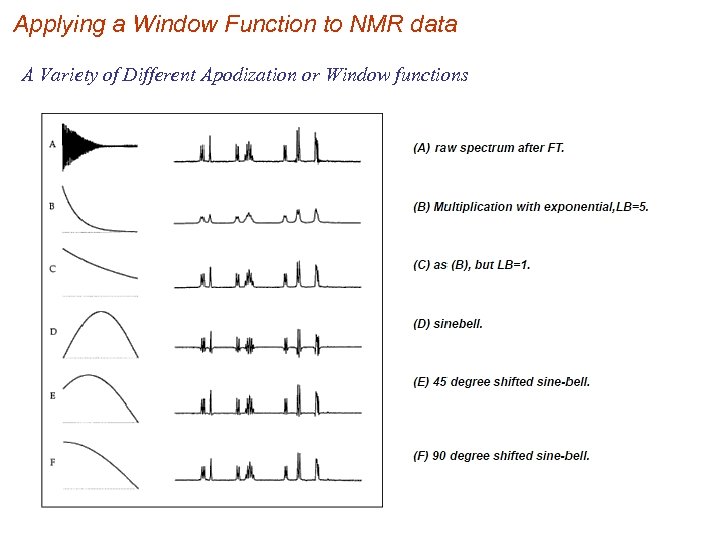
Applying a Window Function to NMR data A Variety of Different Apodization or Window functions
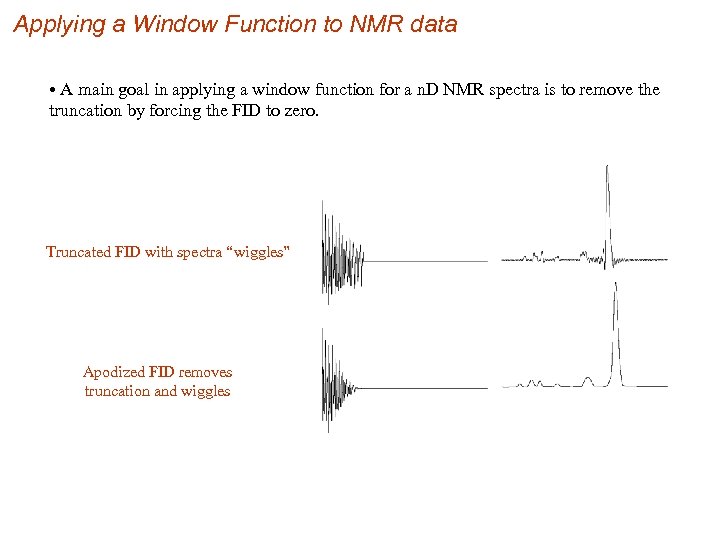
Applying a Window Function to NMR data • A main goal in applying a window function for a n. D NMR spectra is to remove the truncation by forcing the FID to zero. Truncated FID with spectra “wiggles” Apodized FID removes truncation and wiggles
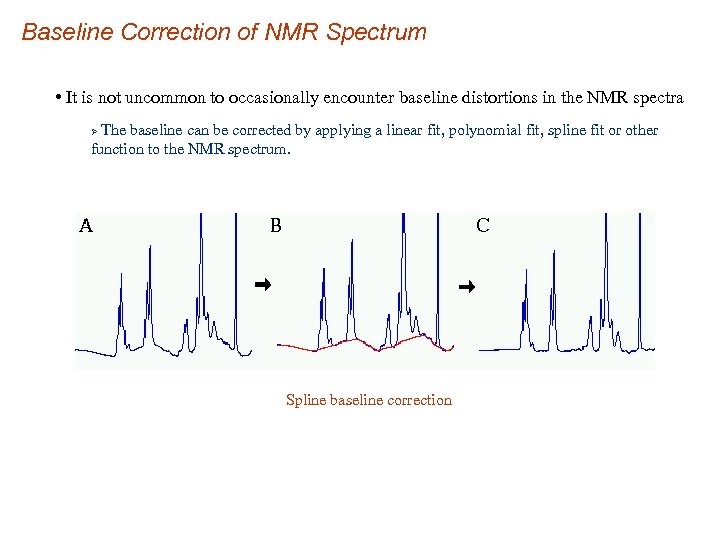
Baseline Correction of NMR Spectrum • It is not uncommon to occasionally encounter baseline distortions in the NMR spectra The baseline can be corrected by applying a linear fit, polynomial fit, spline fit or other function to the NMR spectrum. Ø Spline baseline correction
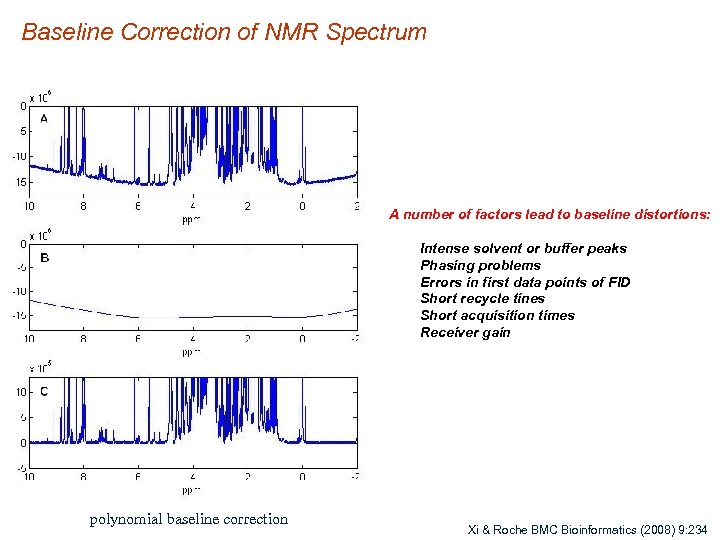
Baseline Correction of NMR Spectrum A number of factors lead to baseline distortions: Intense solvent or buffer peaks Phasing problems Errors in first data points of FID Short recycle tines Short acquisition times Receiver gain polynomial baseline correction Xi & Roche BMC Bioinformatics (2008) 9: 234
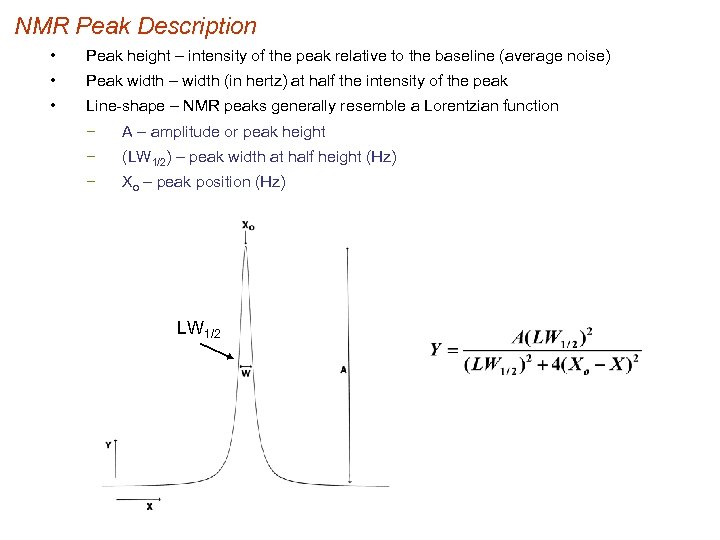
NMR Peak Description • Peak height – intensity of the peak relative to the baseline (average noise) • Peak width – width (in hertz) at half the intensity of the peak • Line-shape – NMR peaks generally resemble a Lorentzian function − A – amplitude or peak height − (LW 1/2) – peak width at half height (Hz) − Xo – peak position (Hz) LW 1/2
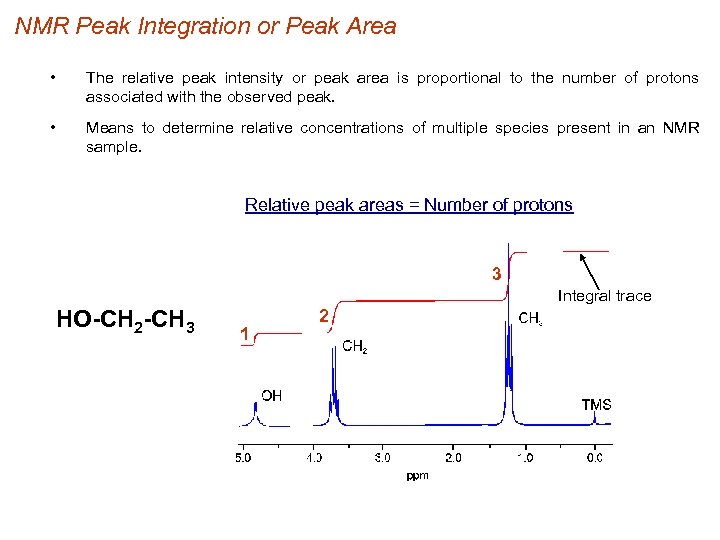
NMR Peak Integration or Peak Area • The relative peak intensity or peak area is proportional to the number of protons associated with the observed peak. • Means to determine relative concentrations of multiple species present in an NMR sample. Relative peak areas = Number of protons 3 Integral trace HO-CH 2 -CH 3 1 2
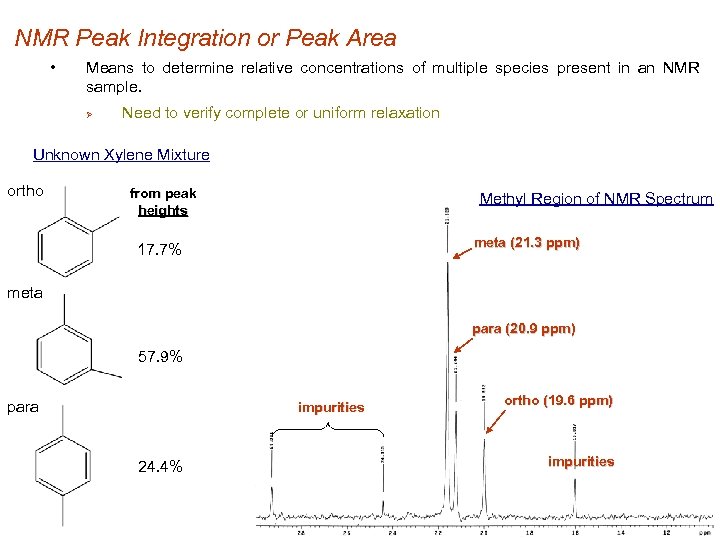
NMR Peak Integration or Peak Area • Means to determine relative concentrations of multiple species present in an NMR sample. Ø Need to verify complete or uniform relaxation Unknown Xylene Mixture ortho from peak heights Methyl Region of NMR Spectrum meta (21. 3 ppm) 17. 7% meta para (20. 9 ppm) 57. 9% para impurities 24. 4% ortho (19. 6 ppm) impurities
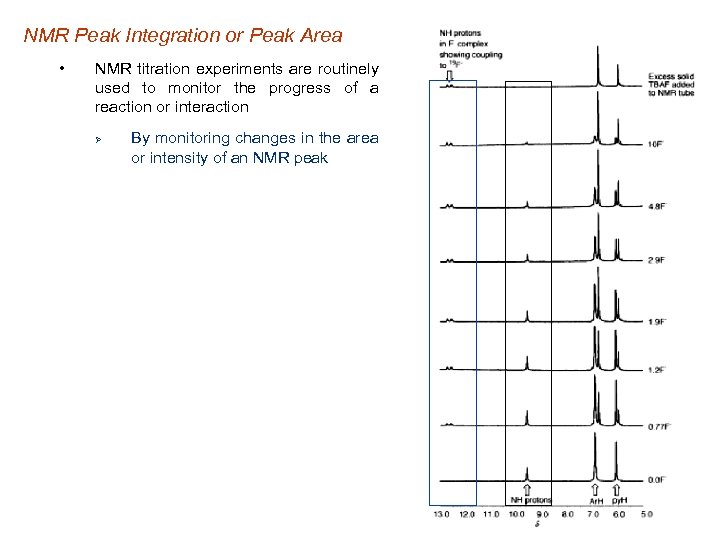
NMR Peak Integration or Peak Area • NMR titration experiments are routinely used to monitor the progress of a reaction or interaction Ø By monitoring changes in the area or intensity of an NMR peak

Peak Picking NMR Spectra One of the basic steps in analyzing NMR spectra is obtaining a list of observed chemical shifts t Usually refereed to as peak picking t Most programs have similar functionality, choice is based on personal preference Ø display the data (zoom, traces, step through multiple spectra, etc) Peak-picking – identify the X, Y or X, Y, Z, A chemical shift coordinate positions for each peak in the n. D NMR spectra Ø Peak Picking List
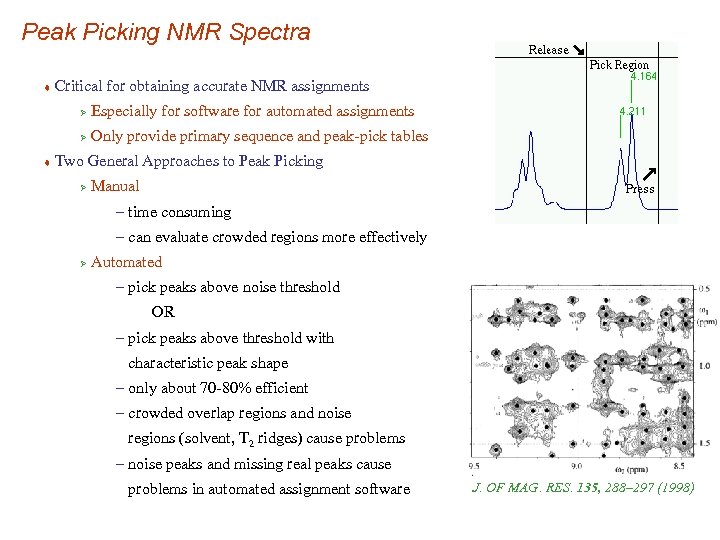
Peak Picking NMR Spectra t Critical for obtaining accurate NMR assignments Ø Ø t Especially for software for automated assignments Only provide primary sequence and peak-pick tables Two General Approaches to Peak Picking Ø Manual – time consuming – can evaluate crowded regions more effectively Ø Automated – pick peaks above noise threshold OR – pick peaks above threshold with characteristic peak shape – only about 70 -80% efficient – crowded overlap regions and noise regions (solvent, T 2 ridges) cause problems – noise peaks and missing real peaks cause problems in automated assignment software J. OF MAG. RES. 135, 288– 297 (1998)
a5a28a855b81c220f30e046e64c03686.ppt