Лекция11_Турбулентное движение жидкости.ppt
- Количество слайдов: 15

Общие закономерности переноса вещества в турбулентном потоке • Турбулентное движение жидкости (гипотезы Прандтля, Кармана, Ландау) • Общие закономерности переноса вещества в турбулентном потоке

Турбулентное движение жидкости Нестационарное, хаотическое движение, при котором скорость течения беспорядочно пульсирует около некоторого среднего значения, называется турбулентным режимом течения. Турбулентные пульсации характеризуются величиной скорости и теми расстояниями, на протяжении которых скорость пульсации претерпевает заметное изменение. Эти расстояния носят название масштаба движения. Самые быстрые пульсационные движения имеют и самый большой масштаб движения. Скорости самых быстрых пульсаций v' имеют порядок v' ΔU, где ΔU — изменение средней скорости на протяжении масштаба пульсации L. Наряду с этими крупномасштабными пульсациями в турбулентном потоке представлены пульсации меньшего масштаба , имеющие меньшие скорости v. Турбулентному потоку можно приписать некоторую эффективную «турбулентную вязкость» μтурб, выразив потери энергии за 1 сек в единице объема уравнением:

Турбулентное движение жидкости Величина не зависит от масштаба движения и является константой, характерной для данного потока. Она равна потере энергии у самых крупномасштабных движений на создание движений меньшего масштаба. Поэтому должно определяться величинами, характеризующими крупномасштабное турбулентное движение. Такими величинами являются только скорости ΔU, масштаб движения L и плотность жидкости ρ (кроме перечисленных величин и μ, никакие другие величины в уравнения гидродинамики не входят). Сравнивая формулы, получаем Соответствующая кинематическая вязкость выразится Пульсационная скорость ΔU по порядку величины равна

Турбулентное движение жидкости Эффективная турбулентная вязкость весьма велика по сравнению с обычной вязкостью Силу трения, действующую на 1 см 2 твердой поверхности где α— некоторый неизвестный множитель пропорциональности. В дальнейшем будем рассматривать два случая турбулентного движения — движение масштаба <<l, т. е. мелкомасштабная турбулентность вдали от твердых стенок, и турбулентные движение вблизи твердых поверхностей. A. Рассмотрим, прежде всего, мелкомасштабное ( <<i ) движение в объеме жидкости. Будем считать, однако, что >> 0, так что движение имеет невязкий характер. Найдем скорость v турбулентных пульсаций масштаба . Выражая через ΔU, находим:

Турбулентное движение жидкости Уменьшению скорости и масштаба соответствует уменьшение числа Рейнольдса для движения масштаба λ по закону При некотором масштабе 0, именуемом внутренним масштабом турбулентности, число Рейнольдса Rе 0, окажется порядка единицы. B. Перейдем теперь к рассмотрению турбулентного движения вблизи твердой поверхности. Рассмотрим, прежде всего, поток жидкости, текущий вдоль бесконечной плоской поверхности (плоскости у = 0). Пусть в среднем поток движется вдоль оси х со средней скоростью vx = U(у). На среднее движение жидкости, происходящее вдоль оси х, накладывается пульсационное движение во всех направлениях. Найдем зависимость U(у)

Турбулентное движение жидкости Учитывая, что τ = const где С 1 — постоянная интегрирования и через v 0 >0 обозначена величина Пусть тогда Для определения постоянной С 1 заметим, что уменьшению масштаба турбулентных пульсаций по мере приближения к стенке соответствует уменьшение числа Рейнольдса При некотором оно становится порядка единицы. В области , носящей название вязкого подслоя, течение имеет вязкий характер. Толщину вязкого подслоя определим условием Или где a – некоторый коэффициент пропорциональности.
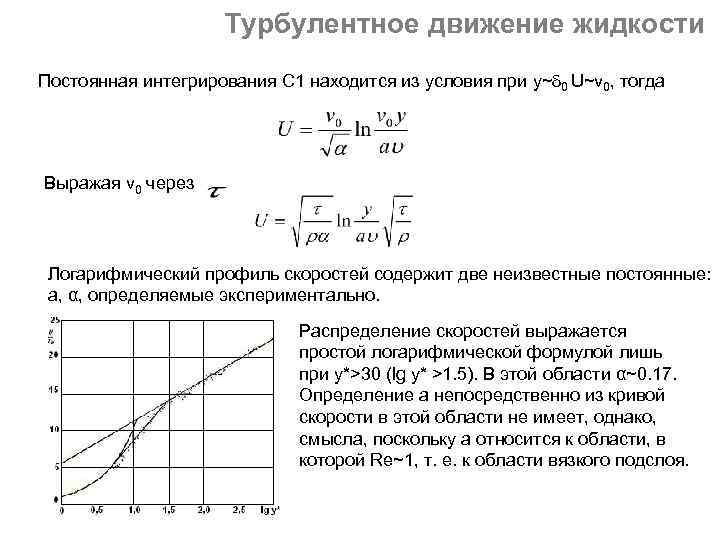
Турбулентное движение жидкости Постоянная интегрирования С 1 находится из условия при y~ 0 U~v 0, тогда Выражая v 0 через Логарифмический профиль скоростей содержит две неизвестные постоянные: а, α, определяемые экспериментально. Распределение скоростей выражается простой логарифмической формулой лишь при у*>30 (lg y* >1. 5). В этой области α~0. 17. Определение а непосредственно из кривой скорости в этой области не имеет, однако, смысла, поскольку а относится к области, в которой Re~1, т. е. к области вязкого подслоя.

Турбулентное движение жидкости Гипотезы о распределении скоростей в вязком подслое. 1. гипотеза Прандтля. В области y< 0 число Re<1 и движение ламинарное. Область названа ламинарным подслоем. В ламинарном подслое напряжение трения распределение скоростей С=0, так как при y=0 U=0. Непосредственное смыкание линейного и логарифмического профиля скоростей не приводит к удовлетворительному согласию с опытным законом распределения. 2. Гипотеза Кармана. Карманом была предложена схема, согласно которой турбулентный поток у твердой стенки может быть разбит на три области: 1) область турбулентного потока, 2) область «буферного» слоя и 3) область ламинарного погранслоя.

Турбулентное движение жидкости 3. гипотеза Л. Д. Ландау, Левича. В вязком подслое турбулентное движение не исчезает внезапно, но постепенно затухает по мере приближения к стенке Определим закон затухания турбулентных пульсаций, т. е. зависимость l от у. В вязком подслое распределение средней скорости (вдоль х) имеет тот же вид, что и при ламинарном течении, т. е. Скорости турбулентных пульсаций в вязком подслое того же порядка, что и средние скорости. В силу уравнения непрерывности нормальная слагающая пульсационной скорости

Турбулентное движение жидкости При. y~ δ 0 на границе вязкого слоя пульсационная скорость v'y имеет тот же порядок величины, что и характерная скорость турбулентного потока v 0. Масштаб пульсационного движения в направлении оси у При чем периоды турбулентных пульсаций Т внутри вязкого подслоя не зависят от расстояния до стенки у, следовательно Поток импульса, переносимый турбулентными пульсациями по направлению к стенке, выражается формулой

Турбулентное движение жидкости Поэтому коэффициент турбулентной вязкости При y< δ 0 можно приближенно считать, что напряжение трения τ совпадает с величиной τ0 , а профиль средней скорости выражается формулой При выводе распределения скоростей в зоне сопряжения турбулентного пограничного слоя и ламинарного подслоя естественно предположить, что в этой области перенос импульса осуществляется турбулентными пульсациями, на которых, однако, сказывается уже влияние вязкости. Для коэффициента турбулентной вязкости в зоне сопряжения естественно написать интерполяционную формулу

Турбулентное движение жидкости а для вязкого напряжения где b — некоторая постоянная. Интегрируя последнюю формулу, находим закон распределения средней скорости в зоне сопряжения Постоянные в и с определяются из условий сопряжения профилей скорости. Окончательно закон распределения для средней скорости

Турбулентное движение жидкости Все выводы могут быть непосредственно перенесены на случай течения в пограничном слое на пластинке или внутри трубы Течение жидкости вдоль полубесконечной пластинки. Турбулентный пограничный слой, образующийся при обтекании гладкой пластинки, в отличие от рассмотренного выше течения вдоль бесконечной поверхности изменяется с координатой х, отсчитываемой от начала пластинки, и имеет конечную толщину d. Внутри пограничный слой имеет логарифмический профиль скорости На границе пограничного слоя, при y=d, скорость течения равна скорости основного потока U 0:

Турбулентное движение жидкости Толщина пограничного слоя d и характерная скорость v 0 изменяются с координатой у так, чтобы эта скорость на границе U 0 была, постоянной величиной. Второе уравнение, связывающее v 0 и d. , может быть составлено на основании следующих соображений. Наклон кривой d(x) равен отношению скоростей нормальных и тангенциальных к пластинке Но на границе слоя vx ~U 0, а vy имеет порядок пульсационной скорости v 0, так что Поскольку v 0 представляет медленно изменяющуюся функцию х, толщину слоя d можно приближенно выразить:

Турбулентное движение жидкости Толщина турбулентного пограничного слоя растет пропорционально расстоянию от начала пластинки. Сила трения, действующая на пластинку, где Кf — коэффициент сопротивления. Простое вычисление показывает, что Кf определяется из уравнения Логарифмический профиль распределения средней скорости можно применить к турбулентному течению жидкости по трубе.
Лекция11_Турбулентное движение жидкости.ppt