1122767.pptx
- Количество слайдов: 19

ОБЩИЕ СВЕДЕНИЯ О МАШИНАХ И МЕХАНИЗМАХ уктурный анализ механизмов

Классификация машин. Энергетические машины Технологические или рабочие Информационные -. ручного управления В зависимости от способа -полуавтоматического и управления -. автоматического действия. различают машины - М а ш и н ы-а в т о м а т ы Механизмы и их назначение. Механизм — часть машины, в которой рабочий процесс реализуется путем выполнения определенных механических движений. Механизм совокуп ность (система) взаимосвязанных тел, предназначенных для преобразования движения. Механизм осуществляет: передачу энергии (движения)

Основные ха. РАКТЕРИСТИКИ МАШИНАМ И МЕХАНИЗМов Производительность машин КПД Масса и габаритные размеры. Основные характеристики машин указывают в их техническом паспорте. Основные ТРЕБОВАНИЯ К МАШИНАМ И МЕХАНИЗМАМ Работоспособность Надежность. Технологичность Экономичность Эргономичность

СТРУКТУРНЫЕ ЭЛЕМЕНТЫ МЕХАНИЗМОВ Механизм связанная система тел (частей ), движущихся как единое целое. Каждое такое тело называют звеном. оно может быть простым или сложным (составным). • звено и элементы сложного звена называют деталями. Звенья различают по конструктивным признакам (зубчатое колесо, поршень, вал), по деформативности (жесткое и гибкое звено), по характеру их движения ( кривоши, коромысло, ползун и т. д. ) Формирование механизма осуществляется с помощью кинематических пар - подвижного соединения частей звеньев. «Силовой поток» от одного звена к другому передается за счет геометрического замыкания (с помощью дополнительной детали ), силового замыкания (прижатия деталей. ) Элементы контакта соединительных частей звеньев: точка, линия, поверхность. . По числу наложенных условий связи S (или степеней подвижности Н) на относительные движения звеньев кинематические пары по предложению акад. И. Артоболевского делят на классы.
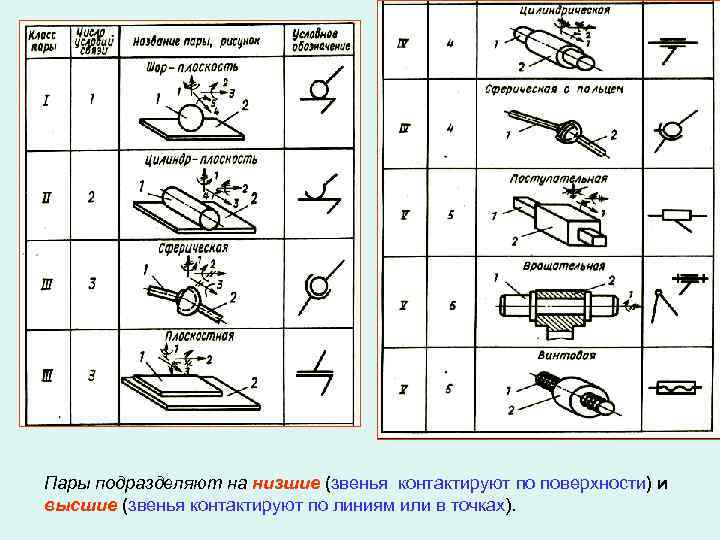
Пары подразделяют на низшие (звенья контактируют по поверхности) и высшие (звенья контактируют по линиям или в точках).
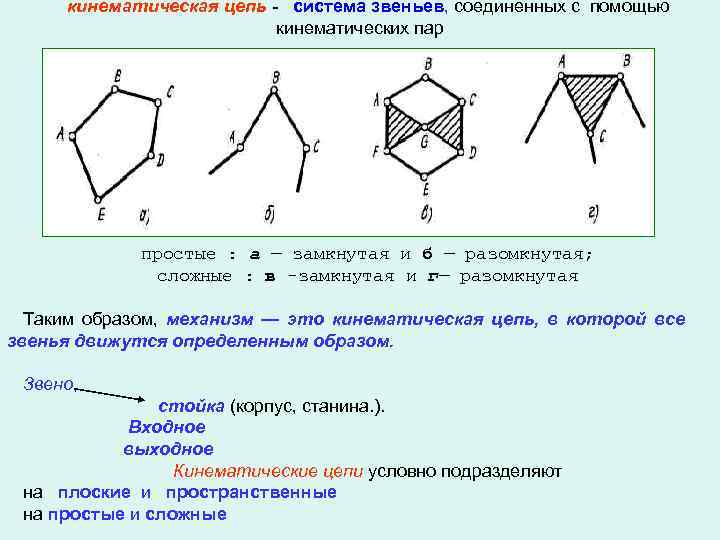
кинематическая цепь - система звеньев, соединенных с помощью кинематических пар простые : а — замкнутая и б — разомкнутая; сложные : в -замкнутая и г— разомкнутая Таким образом, механизм — это кинематическая цепь, в которой все звенья движутся определенным образом. Звено, стойка (корпус, станина. ). Входное выходное Кинематические цепи условно подразделяют на плоские и пространственные на простые и сложные
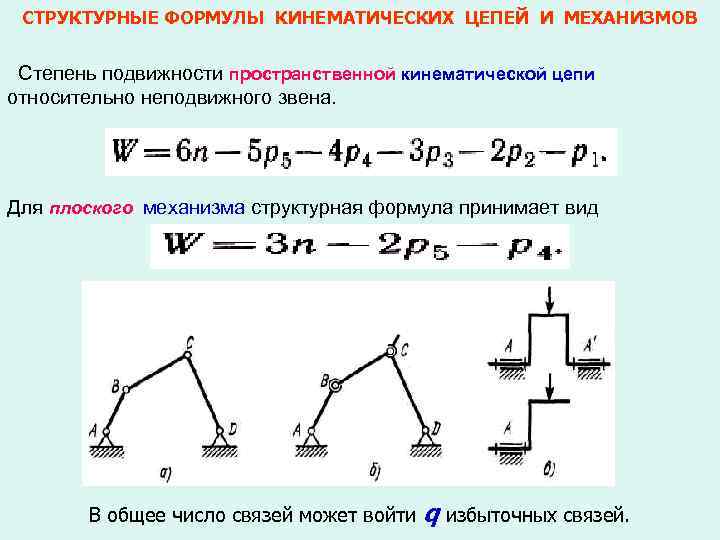
СТРУКТУРНЫЕ ФОРМУЛЫ КИНЕМАТИЧЕСКИХ ЦЕПЕЙ И МЕХАНИЗМОВ Степень подвижности пространственной кинематической цепи относительно неподвижного звена. Для плоского механизма структурная формула принимает вид В общее число связей может войти q избыточных связей.

Основные задачи структурного анализа механизмов: а) определение числа звеньев , структурных групп, числа и вида КП б) определение степени подвижности механизма в) разделение механизма на структурные группы (декомпозиция механизма); г). определение числа контуров и числа избыточных связей Для анализа используют структурную схему — простейшую модель механизма (без указания размеров звеньев). На схеме звенья обозначают цифрами, а пары и характерные точки — буквами. Неподвижное звено показывают штриховкой.
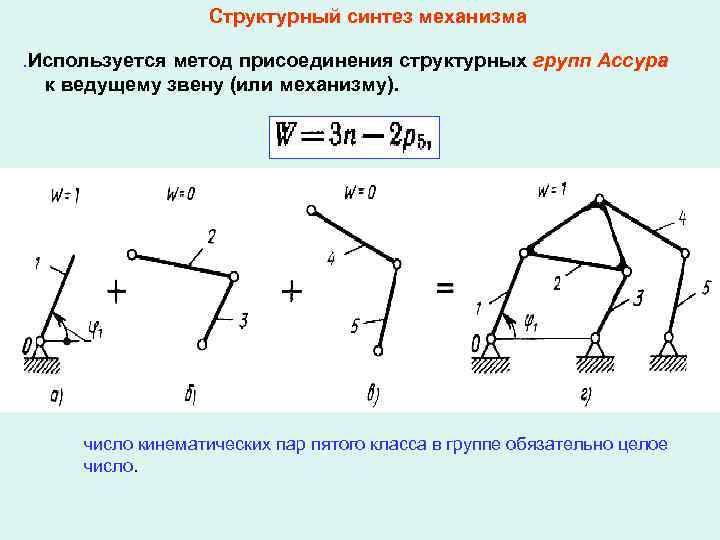
Структурный синтез механизма. Используется метод присоединения структурных групп Ассура к ведущему звену (или механизму). число кинематических пар пятого класса в группе обязательно целое число.
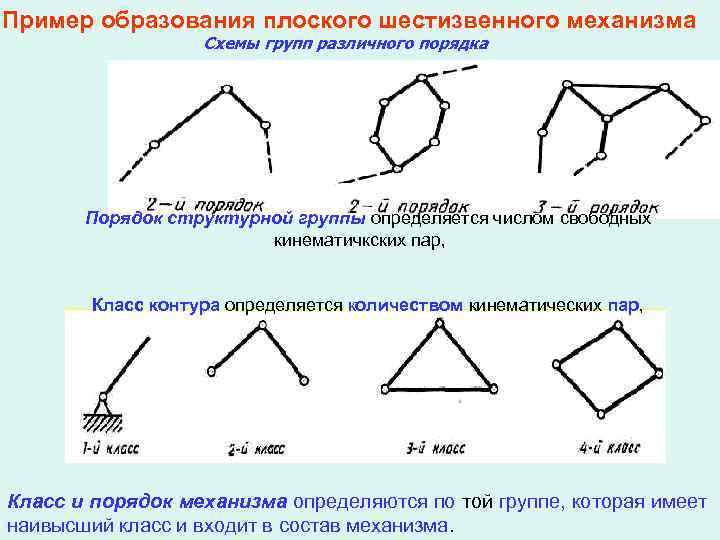
Пример образования плоского шестизвенного механизма Схемы групп различного порядка Порядок структурной группы определяется числом свободных кинематичкских пар, Класс контура определяется количеством кинематических пар, Класс и порядок механизма определяются по той группе, которая имеет наивысший класс и входит в состав механизма.
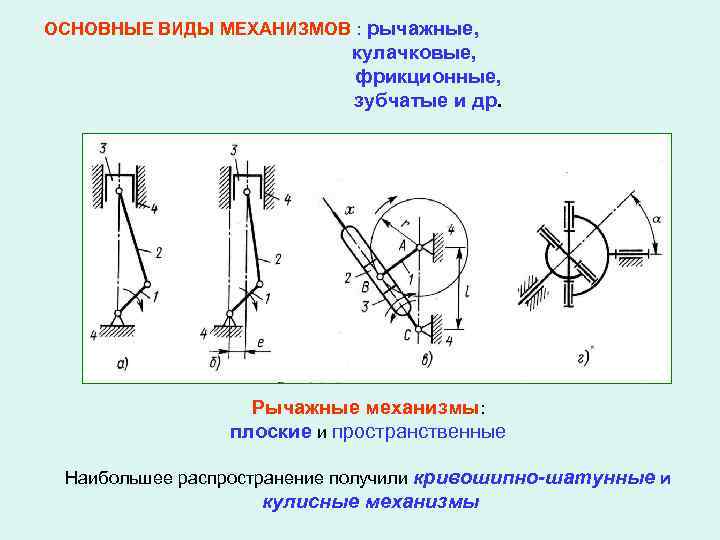
ОСНОВНЫЕ ВИДЫ МЕХАНИЗМОВ : рычажные, кулачковые, фрикционные, зубчатые и др. Рычажные механизмы: плоские и пространственные Наибольшее распространение получили кривошипно-шатунные и кулисные механизмы
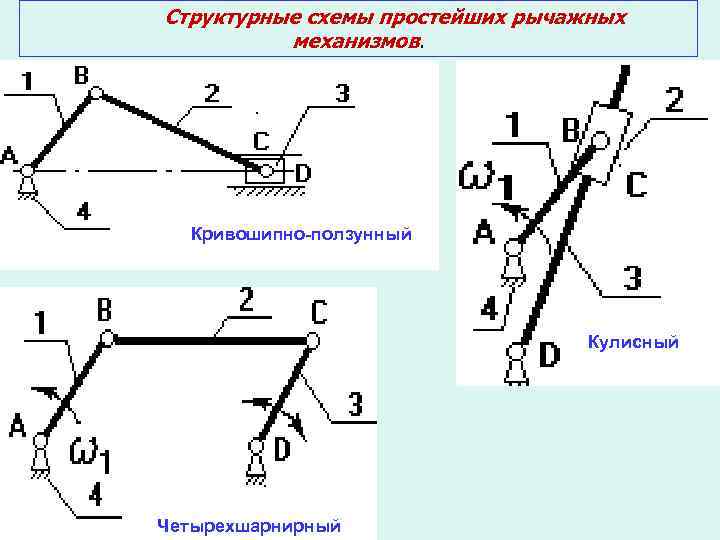
Структурные схемы простейших рычажных механизмов. Кривошипно-ползунный Кулисный Четырехшарнирный
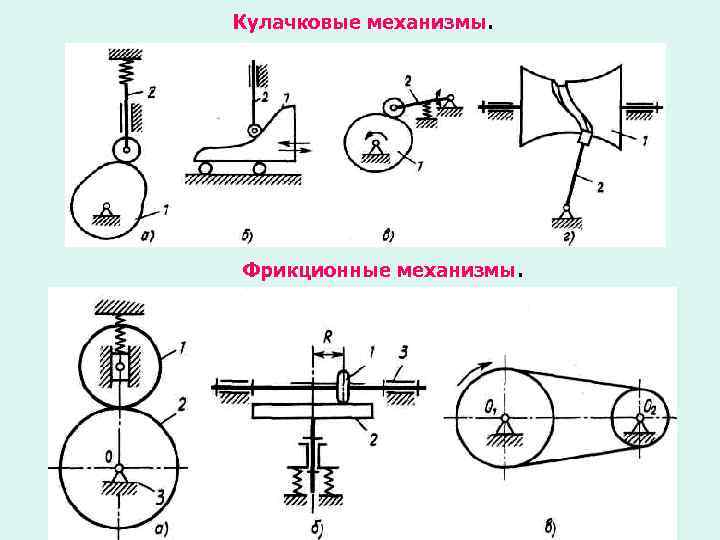
Кулачковые механизмы. Фрикционные механизмы.
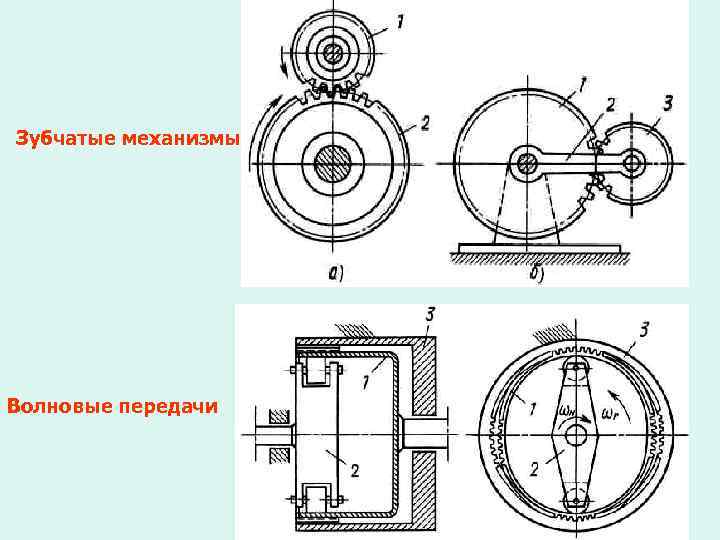
Зубчатые механизмы. Волновые передачи
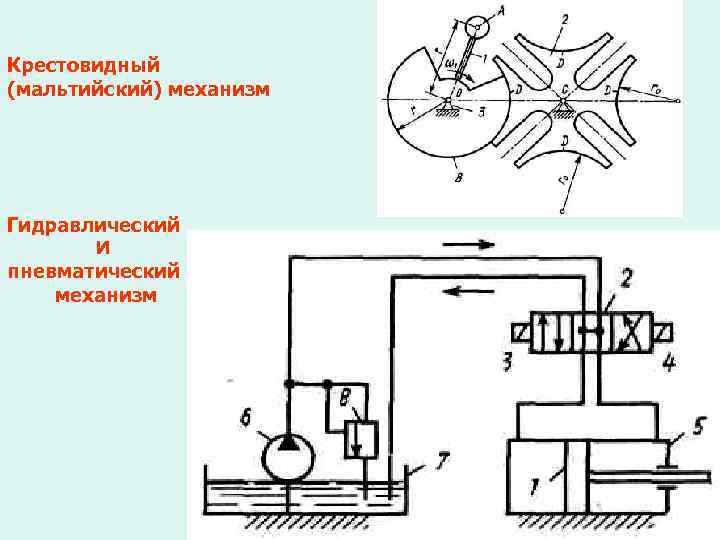
Крестовидный (мальтийский) механизм Гидравлический И пневматический механизм

ПРОЕКТИРОВАНИЕ РЫЧАЖНЫХ МЕХАНИЗМОВ

ВВЕДЕНИЕ Рычажные механизмы широко применяются во многих отраслях машиностроения, в т. ч. в подъемно-транспортных машинах. Постановка задачи оптимизации, кроме установления самого объекта, включает выбор критерия оптимальности и формирование системы ограничений. Известно несколько подходов к выбору критериев оптимальности: один из них – минимум максимального отклонения траектории ведомого звена – рабочего органа, однако для многих производственных задач достаточно требования точности в виде ограничения; для одной группы механизмов – минимум среднего интегрального ускорения ведомого звена или минимум необходимой мощности; для второй группы механизмов – минимальная средняя квадратичная работа сил инерции за цикл движения. Упомянутые выше критерии оптимальности нельзя считать объективными, поскольку затраты на материал звеньев и энергию отражены лишь косвенно, а затраты на изготовление деталей не учтены. Это вносит субъективность в формирование критерия и в результаты оптимизации. Объективным может быть экономический критерий – максимальная производительность труда. Что касается формирования системы ограничений, то обычно не учитывались условия прочности звеньев, хотя без них нельзя обоснованно по- дойти к определению масс и моментов инерции звеньев, а при решении динамических задач массы считались известными. Не учитывались также допустимые углы давления в шарнирах.

Процесс проектирования рычажного механизма включает следующие основные этапы: 1. Производится синтез кинематической схемы (определяются длины звеньев по заданным условиям). 2. Принимается упрощённый закон движения входного звена, определяются скорости и ускорения звеньев, производится приближённый силовой расчёт (определяются реакции в кинематических парах). 3. По найденным усилиям подбираются сечения звеньев и определяются их массы. 4. Производится приведение сил и масс, подбор маховика и определение истинного закона движения звена приведения. 5. При найденном законе движения звена приведения находятся уточнённые значения скоростей и ускорений, определяются более точные величины реакций и производится проверка прочности и жёсткости звеньев. Размеры сечений и массы звеньев последовательно уточняются. Иногда используют более простую последовательность, в которой расчёт ведётся при заданных длинах и массах звеньев, а также при упрощённом законе движения входного звена.

Оптимальный синтез рычажных механизмов Согласно энциклопедическому словарю, задача оптимального проектирования - это экономико-математическая задача, содержащая критерий оптимальности и ограничения и направленная на поиск лучшего в определенных условиях (т. е. оптимального) значения показателя. Оптимизация - отыскание такого решения рассматриваемой задачи, которое дает экстремальное (минимальное или максимальное) значение некоторой функции, называемой целевой [Ю. А. Казик Математический словарь. Таллин. “Валгус” 1985 ]. При оптимальном метрическом синтезе механизма необходимо определить такое сочетание его размеров (внутренние параметры), которое наилучшим образом удовлетворяет требуемым эксплуатационным и качественным показателям (критерии оптимизации и ограничивающие условия). При метрическом синтезе в качественных показателей обычно используются: габариты механизма, точность обеспечения заданных положений или закона движения (функции положения или передаточной функции), условия передачи сил в кинематических парах (углы давления в кинематических парах) и другие показатели. Механизм при оптимальном проектировании характеризуется двумя n-мерными векторами: параметров и качественных показателей. Назначения как параметров, так и качественных показателей могут быть наложены некоторые ограничения в виде равенств или неравенств. Ограничения могут быть: - параметрическими (например, ограничения на длины звеньев механизмов); - дискретизирующими (например, выбор размеров из стандартного ряда); - функциональными (например, условия проворачиваемости звеньев механизма, условия заклинивания кинематических пар). Ограничения формируют область допустимых значений параметров, в пределах которой осуществляется поиск оптимального решения. В пределах этой области могут существовать локальные и глобальный оптимум целевой функции. Целевая функция может быть одномерной или многомерной. При многомерной оптимизации необходимо формирование сложной целевой функции, учитывающей вес каждого из качественных показателей, например, аддитивной
1122767.pptx