Линейно программирование.ppt
- Количество слайдов: 100

ОБЩАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

1. 1 Задачи математического и линейного программирования • Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т. е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих соотношениях выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т. п. ). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» , или «математические методы исследования операций» .

• Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же обычно относят стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие. • Итак, математическое программирование — это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные. • Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразовании, транспортные задачи и т. п. • Построение математической модели экономической задачи включает следующие этапы: 1) выбор переменных задачи; 2) составление системы ограничений; 3) выбор целевой функции.

• Переменными задачи называются величины x 1 , x 2 , . . . , х n , которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора Х= (х1, х2, . . . , хn). • Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физиче скихусловий, например положительности переменных и т. п. • Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

• Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции • F(X) =f (х1, х2, . . . , хn) → max (min) (1. 1) • и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений • (1. 2 ) • Если целевая функция (1. 1) и система ограничений (1. 2) линейны, то задача математического программирования называется задачей линейного программирования.

• В общем случае задача линейного программирования может быть записана в таком виде: • F(Х)=с1 х1+ с2 х2+…+ сn хn → max (min), (1. 3) • • Данная запись означает следующее: найти экстремум целевой функции задачи (1. 3) и соответствующие ему переменные Х = ( х 1 , х 2 , . . . , х n ) при условии, что эти переменные удовлетворяют системе ограничений (1. 4) и условиям неотрицательности (1. 5).

• Допустимым решением (планом) задачи линейного программирования (ЗЛП) называется любой n мерный вектор Х= ( х 1 , х 2 , . . . , х n ) , удовлетворяющий системе ограничений и условиям неотрицательности. • Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР). • Оптимальным решением (планом) ЗЛП называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума. • Так как в данном случае решается задача на экстремум, то возникает вопрос: можно ли использовать классические методы исследования на экстремум функции многих переменных. Применим необходимое условие экстремума функции, которое состоит в том, что частные производные функции многих переменных или равны нулю, или не существуют. В данном случае i=1, 2, …, n. • Но если все с i = 0, то и F = 0, т. е. экстремум функции не обнаруживается. Связано это с тем, что производную можно использовать для определения экстремума только во внутренних точках области решений, а в данном случае экстремум, как будет показано далее, находится на границах области. Отсюда и возникает необходимость разработки специальных методов поиска экстремума.

1. 2 Математические модели простейших экономических задач • Задача использования ресурсов • Для изготовления нескольких видов продукции P 1 , Р 2 , . . . , Р n используют т видов ресурсов S 1 , S 2 , . . . , S m. Это могут быт различные материалы, электроэнергия, полуфабрикаты и т. п. Объем каждого вида ресурсов ограничен и известен (b 1 , b 2 , . . . , bm ). Известно a ij (i = 1, 2, . . . , т; j = 1, 2, . . . , n) — количество каждого i го вида ресурса, расходуемого на производство единицы j - го вида продукции. Кроме того, известна прибыль, получаемая от реализации единицы каждого вида продукции ( с 1 , с 2 , . . . , сп Условия задачи можно представить в виде табл. 1. 1.
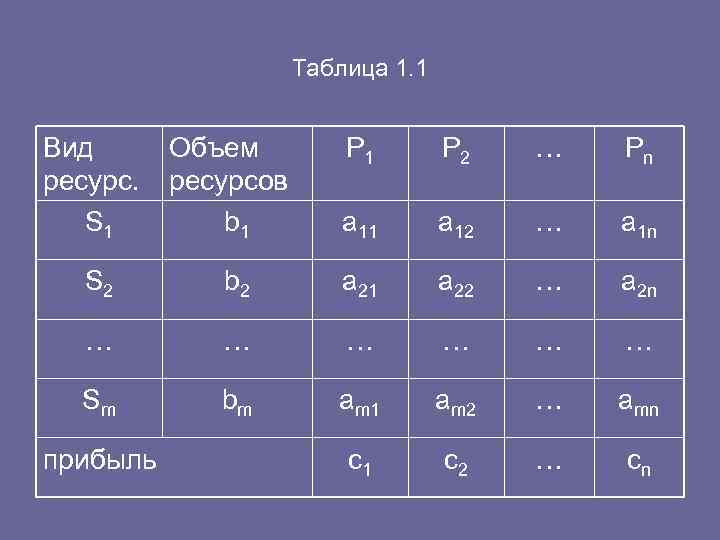
Таблица 1. 1 Вид Объем P 1 P 2 … Pn ресурсов S 1 b 1 a 11 a 12 … a 1 n S 2 b 2 a 21 a 22 … a 2 n … … … … Sm bm am 1 am 2 … amn прибыль c 1 c 2 … cn

• Пусть х j ( j = 1, 2, . . . , n ) — количество каждого вида продукции, ко торое необходимо произвести. Для первого ресурса имеет место неравенство ограничение a 11 x 1+ a 12 x 2+…+ a 1 n xn≤ b 1. • Аналогичные неравенства будут и для остальных видов ресурсов. Сле дует учитывать также, что все значения хj≥ 0, j=1, 2, . . . , n. • Общая прибыль, получаемая от реализации всей продукции, может быть представлена как функция • F(X) = с1 х1 + с2 х2 +. . . + сn хn. • Необходимо эту функцию максимизировать. • Таким образом, математическая модель задачи использования ресурсов запишется в виде • F(X) = с1 х1 + с2 х2 +. . . + сn хn→max, • В более компактной форме целевую функцию и систему ограничений можно записать, используя знак суммирования, • max, • i=1, 2, . . . , m,

• Задача о составлении рациона питания • Требуется составить ежедневный рацион питания животного на основе имеющихся видов кормов так, чтобы общая стоимость использованных кормов была минимальной. При этом животное не должно получать менее определённого количества питательных веществ, например, таких, как жиры, углеводы, белки, витамины и т. п. • Каждый вид корма содержит разную комбинацию этих веществ. Известна цена единицы веса каждого корма. • Пусть имеется п различных кормов (продуктов) Р 1 , Р 2 , . . . , Р n и перечень из т необходимых питательных веществ S 1 , S 2 , . . . , S m. Обозначим через а содержание (в весовых единицах) i го питательного вещества в единице j го корма, а через bi минимальную суточную потребность животного в i м веществе. Через х j обозначим количество каждого вида корма в ежедневном рационе. Очевидно, что х j ≥ 0.
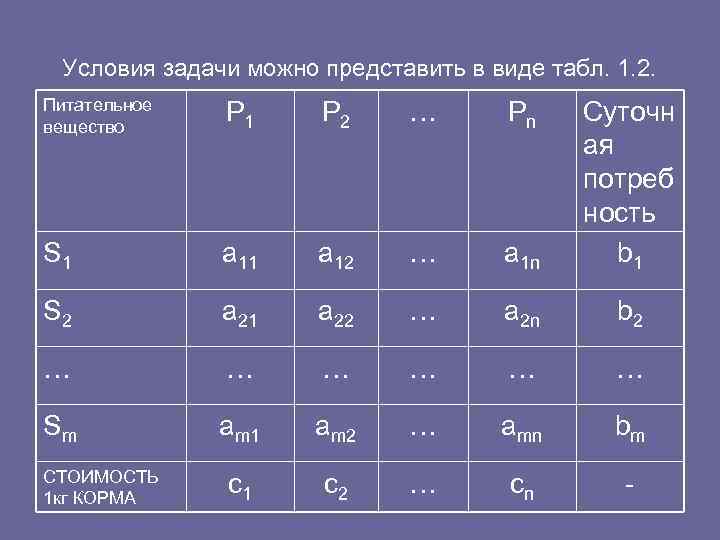
Условия задачи можно представить в виде табл. 1. 2. Питательное вещество P 1 P 2 … Pn Суточн ая потреб ность S 1 a 11 a 12 … a 1 n b 1 S 2 a 21 a 22 … a 2 n b 2 … … … Sm am 1 am 2 … amn bm СТОИМОСТЬ 1 кг КОРМА c 1 c 2 … cn

• Для первого вида питательного вещества неравенство ограничение примет вид a 11 x 1 + a 12 x 2+…+ a 1 n xn≥ b 1. • Аналогичные неравенства будут и для остальных питательных веществ. Следует учитывать также, что все значения хj≥ 0, j=1, 2, . . . , n. • Общие затраты на весь рацион питания животного можно найти на основе линейной функции • F(X) = с1 х1 + с2 х2 +. . . + сn хn. • Необходимо эту функцию минимизировать. • Итак, математическая модель задачи составления рациона питания запишется в виде • F(X) = с1 х1 + с2 х2 +. . . + сn хn→min, • Рассмотрим варианты составления математической модели для следующих задач.

• Задача 1. (Планирование производства. ) • Некоторое предприятие выпускает три типа продукции П 1, П 2, П 3 двумя технологическими способами S 1 и S 2. Количество продукции j-гo вида (j = 1, 2, 3), произведенного i м способом (i = 1, 2) за единицу времени, задано табл. 1. 3. Необходимо так организовывать производство, чтобы получить наибольшую прибыль при реализации продукции по указанной стоимости.
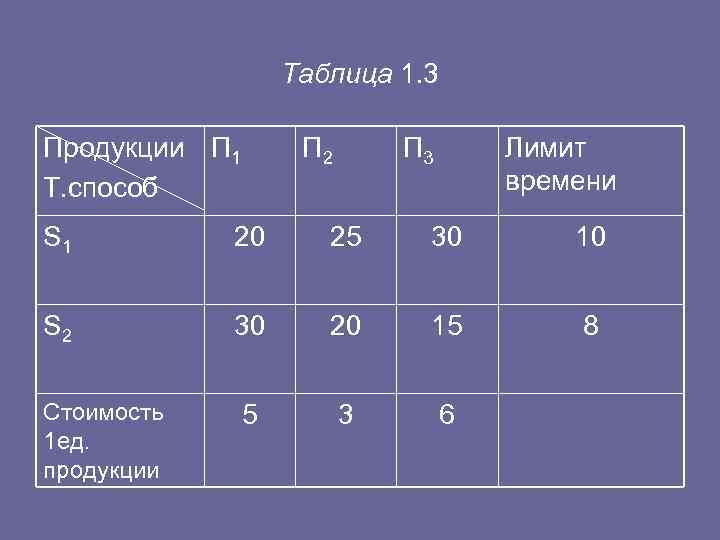
Таблица 1. 3 Продукции П 1 П 2 П 3 Лимит Т. способ времени S 1 20 25 30 10 S 2 30 20 15 8 Стоимость 5 3 6 1 ед. продукции

• Математическая модель задачи • Обозначим через х i j — время, затраченное на изготовление продукции П j ( j = 1, 2, 3) i м способом. Тогда план производства будет иметь вид: • При этом продукции 1 го вида будет выпущено 20 х11+ 30 х 21 , 2 го вида 25 х 12 +20 х 22 , 3 го вида 30 х 13 + 15 х 23. Стоимость всей продукции (обозначим ее за F) равна 5(20 х 11 +30 х 21 )+3(25 х 12 +20 х 22 )+6(30 х 13 +1 должна быть максимальной. Но при этом есть ограничения по времени: х 11 + х 12 + х 13 ≤ 10, х 21 + х 22 + х23 ≤ 8 и очевидно, все хi j ≥ 0. • Окончательно получаем математическую модель задачи • F =5(20 х 11 + 30 х 21 )+3(25 х 12 +20 х 22 )+6(30 х 13 + 15 max, S 1 x 11 x 12 x 13 S 2 x 21 x 22 x 33

• Задача 2. (Задача о смеси. ) • Известно, что при правильном питании человек должен получать в день не менее 20 единиц витамина А, не менее 15 единиц витамина В. Содержание этих витаминов в одной единице каждого из продуктов П 1, П 2, П 3 задано табл. 1. 4. Составить наиболее дешевый рацион питания. Все данные занесены в табл. 1. 4.
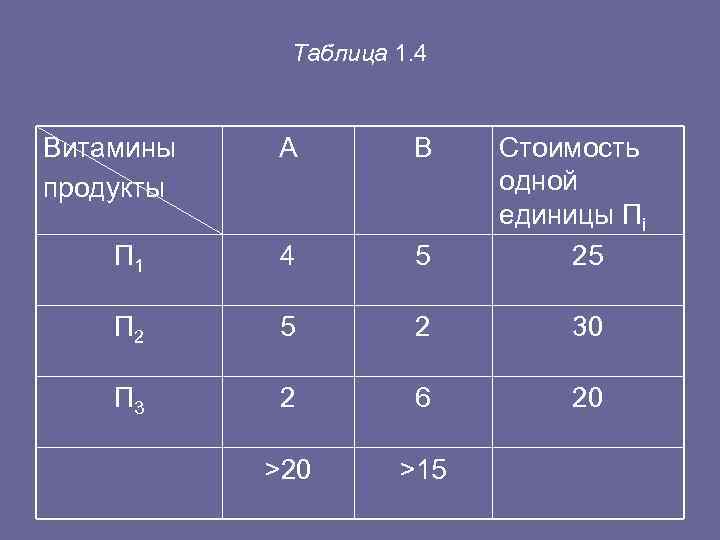
Таблица 1. 4 Витамины А В Стоимость продукты одной единицы Пi П 1 4 5 25 П 2 5 2 30 П 3 2 6 20 >20 >15

• Математическая модель задачи • Пусть хi — количество продукта Пi, потребляемого в день (i=1, 2, 3), тогда стоимость всех продуктов (обозначим F) будет равна F=25 х1 +30 x 2 + +20 х3. При этом количество витамина А равно 4 x 1 + 5 х2 + 2 х3 , витамина В — 5 x 1 + 2 х2 + 6 х3, получаем математическую модель: • F=25 х1 +30 x 2 +20 х3 → min, • Задача 3. (О раскрое материала. ) • Для изготовления некоторого изделия требуется 2 планки по 2 м, 3 — по 2, 5 м и одна трехметровая. Для этого используют 100 досок по 7 м длиной. Как распилить доски, чтобы получить возможно большее число комплектов? • Математическая модель задачи • Рассмотрим возможные варианты распиливания досок. • Таблица 1. 5
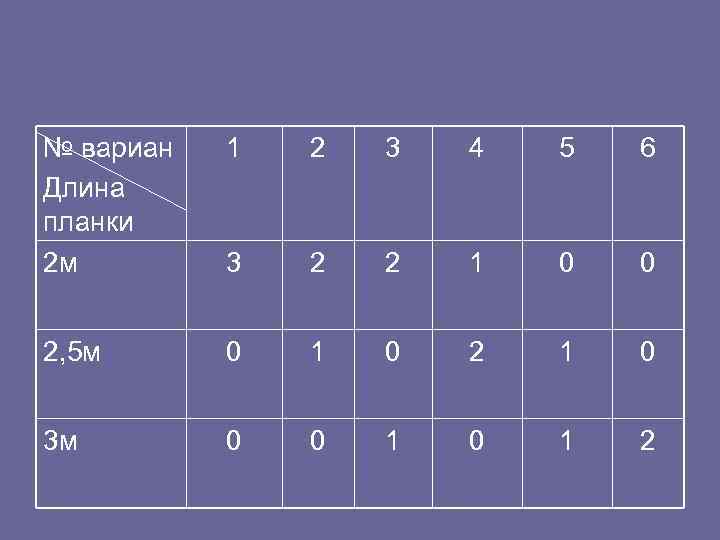
№ вариан 1 2 3 4 5 6 Длина планки 2 м 3 2 2 1 0 0 2, 5 м 0 1 0 2 1 0 3 м 0 0 1 2

• Обозначим через хi— количество досок, распиленных i м способом, тогда заготовок по 2 м получится 3 x 1+ 2 х2 + 2 х3 + х4, по 2, 5 м — x 2 + 2 x 4 + х5; по 3 м — х3 + x 5 + 2 x 6. Обозначим через к — число полученных изделий, тогда • 3 x 1+ 2 х2 + 2 х3 + х4 = или 2(3 x 1+ 2 х2 + 2 х3 + х4 )=к, • x 2 + 2 x 4 + х5 = или 3(x 2 + 2 x 4 + х5 )=к, • х 3 + x 5 + 2 x 6=к. Исключим к. • 2(3 x 1+ 2 х2 + 2 х3 + х4 )= 3(x 2 + 2 x 4 + х5 ) или 6 x 1+ х2 + 4 х3 4 х4 3 х5 =0, • 2(3 x 1+ 2 х2 + 2 х3 + х4 )= х3 + x 5 + 2 x 6 или 6 x 1+ 4 х2 + 3 х3 +2 х4 х5 2 х6=0. • Окончательно получим математическую модель • к=х 3 + x 5 + 2 x 6→ max, • • все хi ≥ 0. • Мы видим, что различные экономические задачи приводят к одному и тому же типу математических задач. Задачи такого типа решаются методами линейного программирования.

1. 3. Каноническая форма задачи линейного программирования • В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В том случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Она может быть представлена в координатной, векторной или матричной форме записи. • 1. Каноническая задача линейного программирования в координатной записи имеет вид

• F(X) = с1 х1 + с2 х2 +. . . + сn хn→max (min), Данную задачу можно записать, используя знак суммирования: max (min), i=1, 2, . . . , m,

• 2. Каноническая задача линейного программирования в векторной записи имеет вид • F(X)=C·X → max (min), • A 1 x 1+ A 2 x 2+…+ An xn=A 0 , • X ≥ θ. • В данном случае введены векторы • Х=(х1, х2, …. , , хn), С=(с1, с2, …. , сn), • θ =(0, 0, …, 0). • Здесь C·X ― скалярное произведение векторов C и X. • 3. Каноническая задача линейного программирования в матричной записи имеет вид • F(X) = CX → max (min), • AX = A 0 , X≥θ, • где Здесь А ― матрица коэффициентов системы уравнений, Х ― матрица столбец переменных задачи, АО — матрица столбец правых частей системы ограничений. • Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной записи имеют вид • F(X) = CX→ max, или F(X) = CX→ min, • AX ≤A 0 , X≥θ AX ≥A 0 , X≥θ.

1. 4. Приведение общей задачи линейного программирования к канонической форме • В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако при со ставлении математических моделей экономических задач ограничения в основном формируются в системы неравенств, поэтому необходимо уметь переходить от системы неравенств к системе уравнений. Это может быть сделано следующим образом. • Возьмем, например, линейное неравенство а 1 х1 + а 2 х2 +. . . + аn хn ≤ b и прибавим к его левой части некоторую величину хn+1, такую, чтобы неравенство превратилось в равенство а 1 х1+ а 2 х2+. . . +аn хn+1 =b, где хn+1 =b-а 1 х1 -а 2 х2 - -. . . - аn хn. Неотрицательная переменная хn+1≥ 0 называется дополнительной переменной. • Следующая теорема дает основание для возможности такого преобразования.

• Теорема 1. 1. Каждому решению β=(β 1, β 2, … βn) неравенства а 1 х1 +а 2 х2 + +. . . + аn хn≤ b соответствует единственное решение =(β 1, β 2, … βn , βn+1) уравнения а 1 х1 + а 2 х2 +. . . + аn хn+1 =b, и неравенства хn+1 ≥ 0, и, наоборот, каждому решению уравнения и неравенства соответствует единственное решение β неравенства. • Доказательство. Пусть β=(β 1, β 2, … βn) — решение неравенства а 1 х1 + а 2 х2 +. . . + аn хn≤ b. Тогда а 1 β 1 + а 2 β 2 +. . . + аn βn≤ b или 0≤ b- (а 1 β 1 + а 2 β 2 +. . . + аn βn)= βn+1. • Подставив в уравнение вместо переменных значения β 1, β 2, … βn , βn+1, получим а 1β 1+а 2β 2+. . . +аn βn+βn+1= а 1β 1+а 2β 2+. . . +аn βn+ b-(а 1 β 1 +а 2 β 2 +. . . +аnβn)= b. • Таким образом, решение удовлетворяет уравнению и неравенству. Значит, доказана первая часть теоремы. Аналогично доказывается обратное.

• Например, если в задаче использования ресурсов в левую часть каждого уравнения системы ограничений добавить положительную переменную хn+1, i=1, 2, . . . , m, то получится система уравнений ограничений В задаче составления рациона питания система ограничений неравенств имеет вид В этом случае система уравнений ограничений получится, если в левой части каждого неравенства вычесть соответствующую неотрицательную дополнительную переменную Полученная таким образом система уравнений ограничений вместе с условиями неотрицательности переменных, т. е. хj ≥ 0, j = 1, 2, . . . , n , и целевой функцией является канонической формой записи задачи линейного программирования. • Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значение.

• Задачи для самостоятельного решения • Записать экономико математические модели следующих задач: • 1. Для выпуска изделий двух типов (А и В) на заводе используется сырье четырех видов (I, III и IV). Расход сырья каждого вида на изготовление единицы продукции задан табл. 1. 6. Запасы сырья составляют: I вида — 21 ед. , II вида — 8 ед. , III вида— 12 ед. , IV вида — 5 ед. Выпуск одного изделия типа А приносит 3 ден. ед. прибыли, одного изделия типа В — 2 ден. ед. Составить план производства, обеспечивающий наибольшую прибыль. • Таблица 1. 6
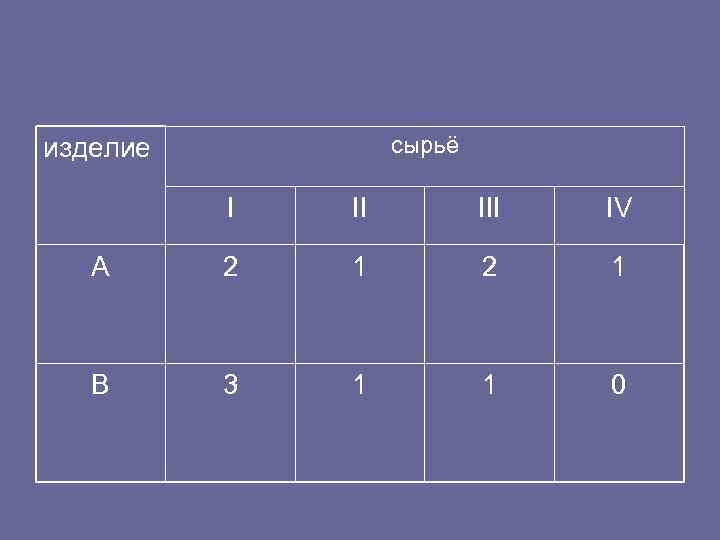
изделие сырьё I III IV А 2 1 2 1 В 3 1 1 0

• 2. На четырех станках (I, III и IV) обрабатываются два вида деталей (А и В), причем каждая деталь проходит обработку на всех станках. Известны время обработки деталей на каждом станке, время работы станков в течение одного цикла производства и прибыль, получаемая от выпуска одной детали каждого вида. Эти данные приведены в табл. 1. 7. Составить план производства, обеспечивающий наибольшую прибыль при условии, что количество деталей вида В не должно быть меньше количества деталей вида А.
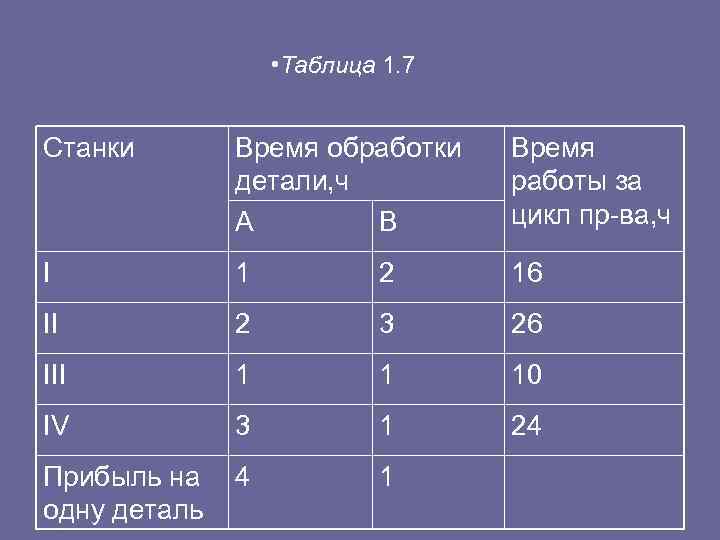
• Таблица 1. 7 Станки Время обработки Время детали, ч работы за А В цикл пр ва, ч I 1 2 16 II 2 3 26 III 1 1 10 IV 3 1 24 Прибыль на 4 1 одну деталь

• 3. Совхоз закупает удобрения двух видов. В единице массы удобрения I вида содержатся 3 усл. ед. химического вещества а, 2— вещества b и 1— вещества с; в единице массы удобрения II вида — 1 усл. ед. вещества а, 1—вещества b и 1— вещества с. На 1 га почвы необходимо внести не менее 9 усл. ед. вещества а, 8 — вещества b, 6 — вещества с. Составить наиболее экономичный план закупки удобрений (в расчете на 1 га), если цены удобрений (на 1 ед. массы) таковы: I вида — 3 ден. ед. , II вида — 4 ден. ед. • 4. Для производства двух видов продукции (А и В) предприятие должно использовать оборудование трех видов (I, III), имеющееся в количествах соответственно 8, 6, 9 ед. По техническим условиям для производства 1 шт. продукции А требуется 2 ед. оборудования I вида, 1 ед.

• оборудования — II вида и 3 ед. оборудования — III вида, а для производства 1 шт. продукции В — 2, 2 и 0 ед. соответствующих видов оборудования. Известно, что от реализации 1 шт. продукции А предприятие получит 1 ден. ед. прибыли, 1 шт. продукции В — 3 ден. ед. Сколько единиц продукции каждого вида должно выпустить предприятие, чтобы получить наибольшую прибыль? • 5. Можно закупить корм двух видов (I и II). В каждой единице корма I вида содержатся 1 ед. витамина А, 2 ед. витамина В и нет витамина С; в каждой единице корма II вида — 2 ед. витамина А, 1 ед. витамина В и 1 ед. витамина С. Животному необходимо дать в сутки не менее 10 ед. витамина А , 10 ед. витамина В и 4 ед. витамина С. Составить наиболее дешевый рацион питания животного, если стоимость единицы корма I вида равна 2 ден. ед. , а стоимость единицы корма II вида — 5 ден. ед.

• 6. Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: мо локо и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в табл. 1. 8. • Таблица 1. 8
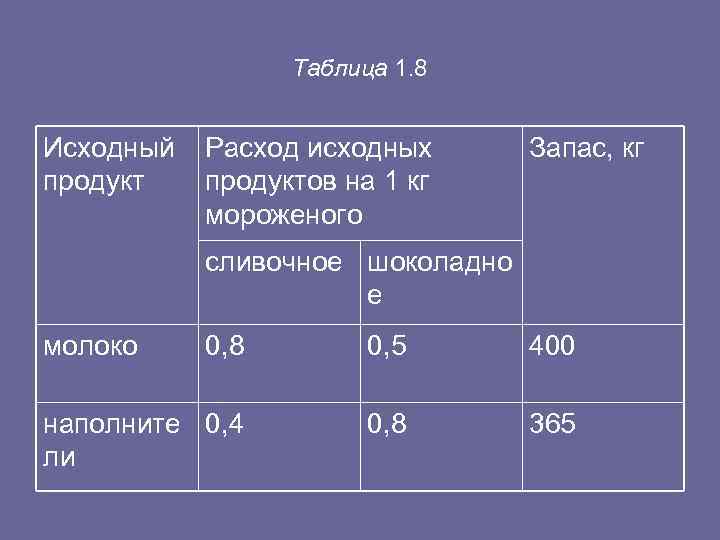
Таблица 1. 8 Исходный Расход исходных Запас, кг продуктов на 1 кг мороженого сливочное шоколадно е молоко 0, 8 0, 5 400 наполните 0, 4 0, 8 365 ли

• Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед. , шоколадного — 14 ден. ед. Определить количество мороженого каждого вида, которое должна производить фирма, чтобы доход от реализации продукции был мак симальным.

2. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ • 2. 1. Задача с двумя переменными • Пусть требуется найти максимальное значение функции • F(X) = с1 х1 + с2 х2 (2. 1) • при ограничениях

• Допустим, что система ограничений (2. 2) совместна, т. е. имеет решение, а многоугольник ее решений (ОДР) ограничен. Каждое из неравенств (2. 2) определяет полуплоскость с границей , i = 1, 2, . . . , т или х1 = 0, х2 = 0. Представим этот многоугольник на плоскости Ох1 х2 (рис. 2. 1). Рис. 2. 1

• Линейная функция (2. 1) при фиксированных значениях F(X) является уравнением прямой линии c 1 x 1+ c 2 x 2=const. • Изобразим прямую, соответствующую линейной функции, при F(X) = 0. Эта прямая пройдет через начало координат. Другим значениям F(X) будут соответствовать прямые, параллельные другу. • Прямая, уравнение которой получено из целевой функции задачи при равенстве ее постоянной величине, называется линией уровня. • Известно, что коэффициенты при переменных в линейном уравнении являются координатами нормального вектора к соответствующей прямой или плоскости.

• Следовательно, нормальный вектор линий уровня и имеет координаты с1 и с2, т. е. = (с1, с2). • Если перемещать линию уровня параллельно ее начальному положению в направлении вектора , то для данного случая (см. рис. 2. 1) последней точкой, в которой линия уровня коснется ОДР, окажется точка С. Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, называется опорной прямой.

• Теорема 2. 1. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали, и убывают при перемещении в противоположном направлении. • Доказательство. Пусть F(X) =c 1 x 1+ c 2 x 2— целевая функция. Изобразим систему координат Ох1 х2 и нормаль = (с1, с2), проведенную из начала координат (рис. 2. 2). Проведем две линии уровня перпендикулярно вектору. Возьмем на первой линии точку Р(х'1, х'2), а на второй линии точку М(х1, х2) так, чтобы вектор РМ был параллелен вектору. Проведем векторы ОМ и ОР. Вектор ОМ имеет координаты х1, х2, т. е. координаты точки М, а вектор ОР ― координаты точки Р.
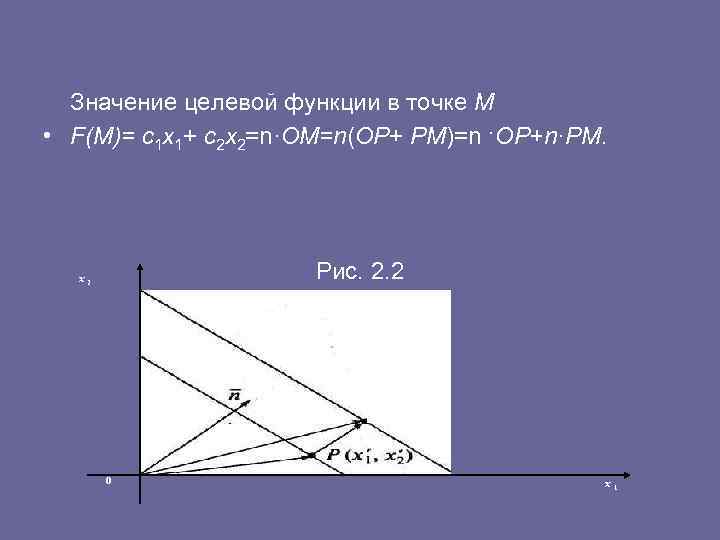
Значение целевой функции в точке М • F(M)= c 1 x 1+ c 2 x 2=n·ОМ=n(ОР+ РМ)=n ·ОР+n·РМ. x 2 Рис. 2. 2 M(x 1 , x 2 ) 0 x 1

• Но n·ОР равно значению целевой функции в точке Р, т. е. F(P). По определению скалярного произведения · РМ= где φ— угол между векторами и РМ. Если и РМ направлены в одну сторону, то φ= 0 и cosφ= 1. Тогда F(M)= F(P)+ F(M)> F(P). Если и РМ направлены в противоположные стороны, то cosφ = 1 и F(M) < F(P). Что и требовалось доказать (Ч. т. д). • Алгоритм решения ЗЛП с двумя переменными графическим методом таков: • Строится область допустимых решений. • Строится вектор = (с1, с2) с точкой приложения в начале координат. • Перпендикулярно вектору проводится одна из линий уровня, например линия уровня, соответствующая уравнению с1 х1 + с2 х2 = 0.

• Линия уровня перемещается до положения опорной прямой. На этой прямой и будет находиться максимум или минимум функции. • В зависимости от вида ОДР и целевой функции F(X) задача может иметь единственное решение (рис. 2. 3, а), бесконечное множество решений (рис. 2. 3, б) или не иметь ни одного оптимального решения (рис. 2. 3, в).
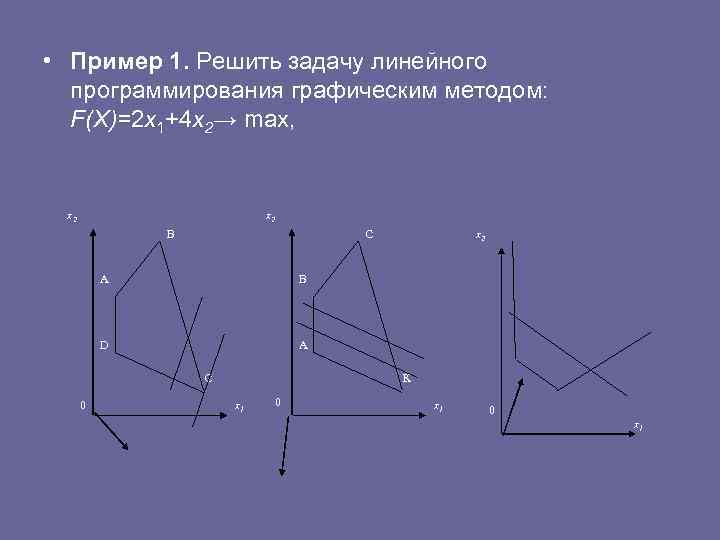
• Пример 1. Решить задачу линейного программирования графическим методом: F(X)=2 x 1+4 x 2→ max, x 2 B С x 2 A В D А C К 0 x 1 0 x 1

• Решение. Изобразим на плоскости систему координат Ох1 х2 и построим


• граничные прямые области допустимых решений (номера прямых соответствуют их порядковому номеру в системе). Область допустимых решений определяется многоугольником OABCD (рис. 2. 4). • Для линий уровня 2 х1 + 4 х2 = с (с = const) строим нормальный вектор = (2, 4). • Рис. 2. 4 • граничные прямые области допустимых решений (номера прямых соответствуют их порядковому номеру в системе). Область допустимых решений определяется многоугольником OABCD (рис. 2. 4). • Для линий уровня 2 х1 + 4 х2 = с (с = const) строим нормальный вектор = (2, 4).

• Рис. 2. 4 • граничные прямые области допустимых решений (номера прямых соответствуют их порядковому номеру в системе). Область допустимых решений определяется многоугольником OABCD (рис. 2. 4). • Для линий уровня 2 х1 + 4 х2 = с (с = const) строим нормальный вектор = (2, 4). • Перпендикулярно вектору построим одну из линий уровня (на рис. 2. 4 она проходит через начало координат). Так как задача на максимум, то перемещаем линию уровня в направлении вектора до опорной прямой. В данном случае опорной прямой является прямая, проходящая через точку пересечения граничных прямых L 1 и L 2, т. е. через точку В = L 1∩L 2. Для определения координат точки В решаем систему уравнений

• Получаем х1 = 3, х2 = 6. Это и будет оптимальное решение данной задачи, которому соответствует максимальное значение целевой функции • max F(X) = 2 · 3 + 4 · 6 = 30. • Пример 2. Найти минимум функции F(X)=2 x 1+x 2→ min при ограничениях

• Отличие этого примера от предыдущего состоит в том, что здесь ищется не максимум, а минимум функции F. Областью решений данной системы ограничений является треугольник АВС (рис. 2. 5). На рисунке изображены также исходная линия уровня и вектор q = (2; 1), показывающий направление движения этой линии для достижения максимума функции F. Так как требуется найти минимум этой функции, то будем передвигать исходную линию уровня в сторону, противоположную вектору q. Как видно из рис. 2. 5, минимум функции F достигается в угловой точке А, координаты которой служат решением системы уравнений
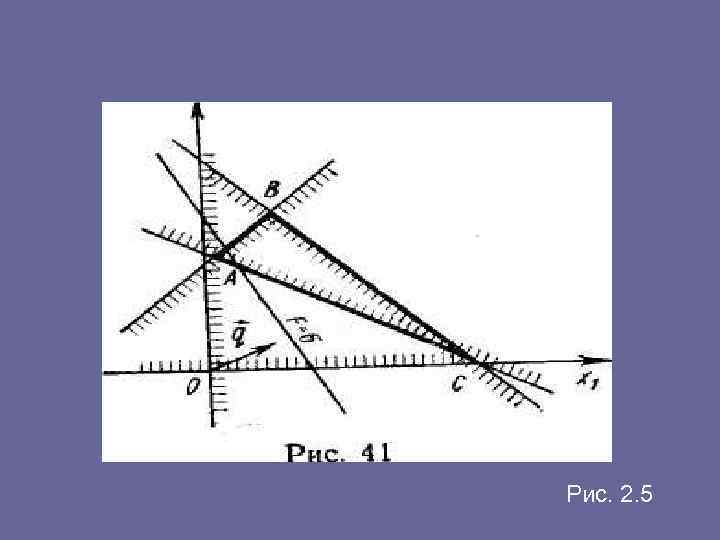
Рис. 2. 5
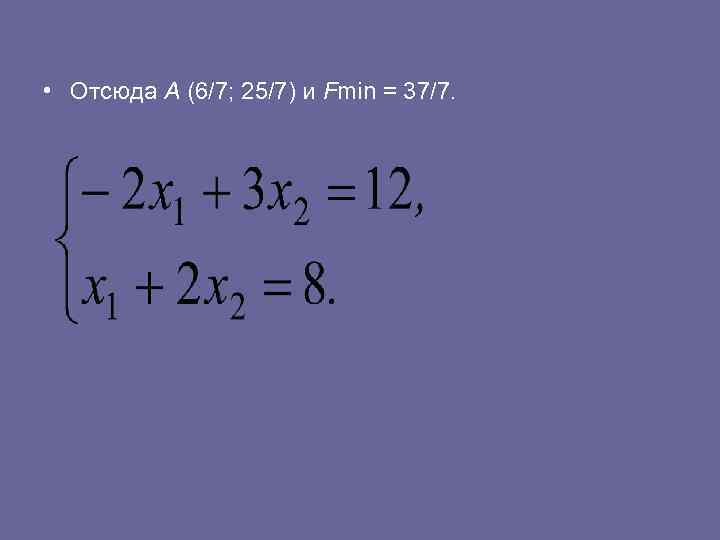
• Отсюда А (6/7; 25/7) и Fmin = 37/7.

2. 2. Графический метод решения задач линейного программирования с п переменными • Графическим методом можно решить задачи линейного программирования, имеющие каноническую форму и удовлетворяющие условию n- r ≤ 2, где n—число неизвестных системы; r — ранг системы векторов условий (число линейно независимых уравнений системы). • Если уравнения системы ограничений линейно независимы, то r = т, где т — число уравнений. • Рассмотрим алгоритм метода на конкретном примере. • Пример. Решить графическим методом задачу • F(X)=x 1+x 2+5 x 3+3 x 4→ max,
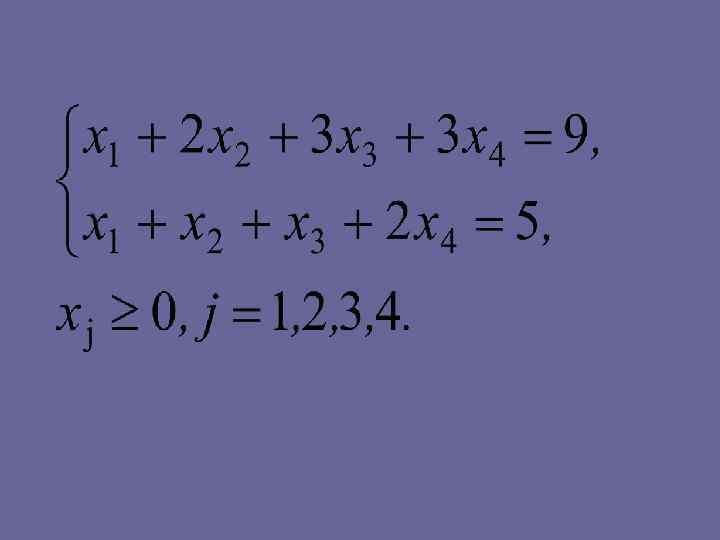

• Решение. Проверяем, применим ли графический метод при решении данной задачи. Нетрудно видеть, что любые два из векторов условий, например линейно независимы, так как их координаты непропорциональны. Поэтому ранг системы векторов условий r=2. Находим n- r= 4 2 = 2 ≤ 2. Следовательно, метод применим. • Приведем систему уравнений ограничений к равносильной, с помощью линейных преобразований, предварительно записав её в матричной форме:

• Таким образом, получили систему: Выразим переменные х1 и х2: х2=4 2 х3 х4 х1=9 2 х2 3 х3 3 х4=9 2(4 2 х3 х4) 3 х3 3 х4=9 8+4 х3+2 х4 3 х3 3 х4=1+х3 х4 Т. к. х1≥ 0 и х2≥ 0, то систему уравнений мы записываем в виде системы неравенств:

• В результате получим эквивалентную задачу линейного программирования с двумя переменными, которая решается графическим методом • F(X)= 1+х3 х4+4 2 х3 х4+5 х3+3 х4=5+4 х3+ х4 → max х3≥ 0, х4≥ 0. Изобразим на плоскости систему координат О х 1 х 2 и построим граничные прямые области допустимых решений. Находим оптимальное решение эквивалентной

• задачи и соответствующее ему максимальное значение целевой функции: С(2, 0), F(C)=5+4· 2+0=13 • Используем систему ограничений исходной задачи, приведенную к каноническому виду, и оптимальное решение задачи с двумя переменными для нахождения оптимального решения исходной задачи: • х2=4 2 х3 х4=4 2· 2 0=0, х1=1+х3 х4=1+2 0=3. • Следовательно, X=(3, 0, 2, 0); F(X)=3+0+5· 2+3· 0=13. • Ответ: max F(X)= 13, при X=(3, 0, 2, 0).

• Задачи для самостоятельного решения • Найти максимум функции F при заданных ограничениях:
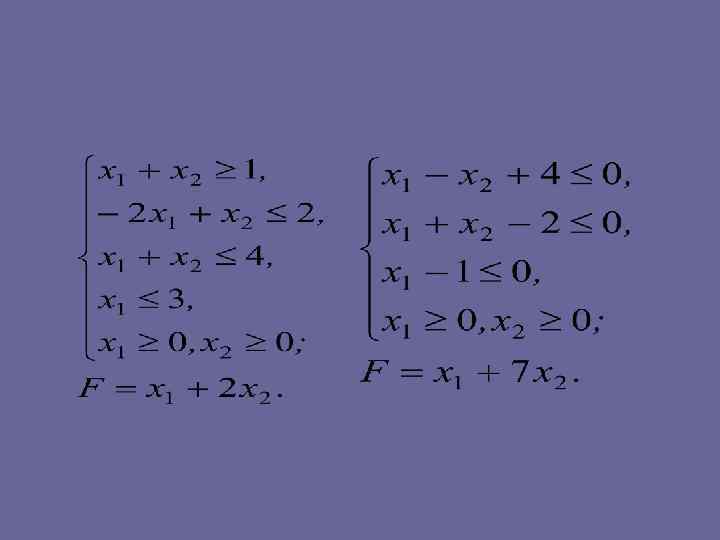
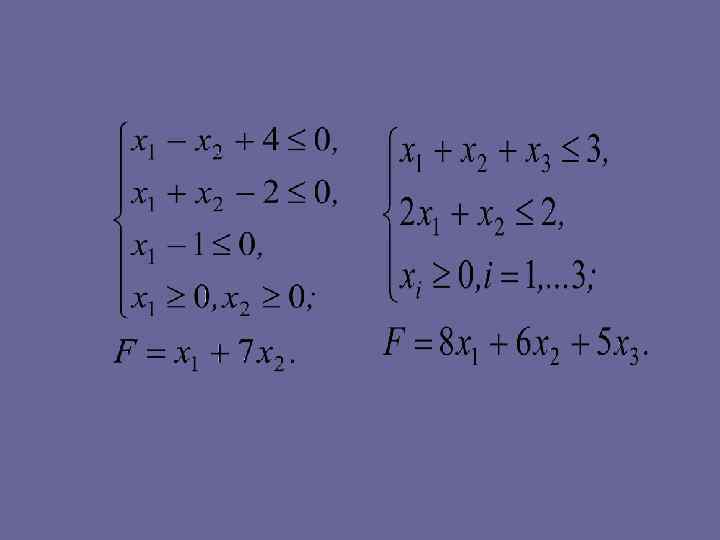
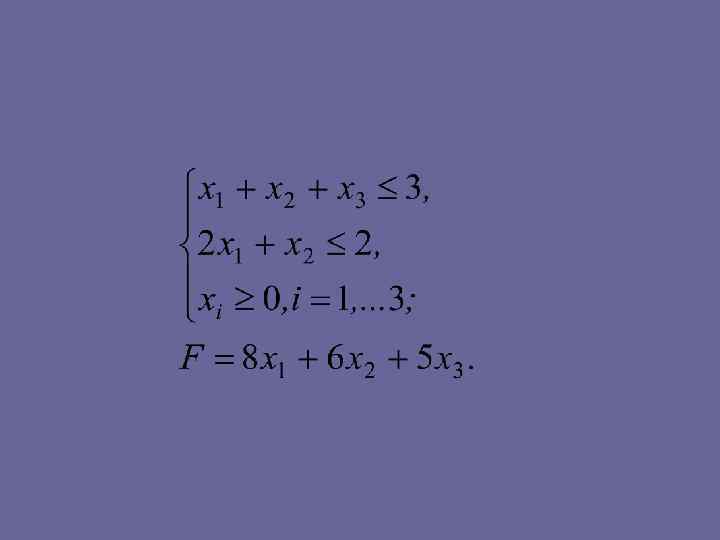

• Найти минимум функции F при заданных ограничениях:
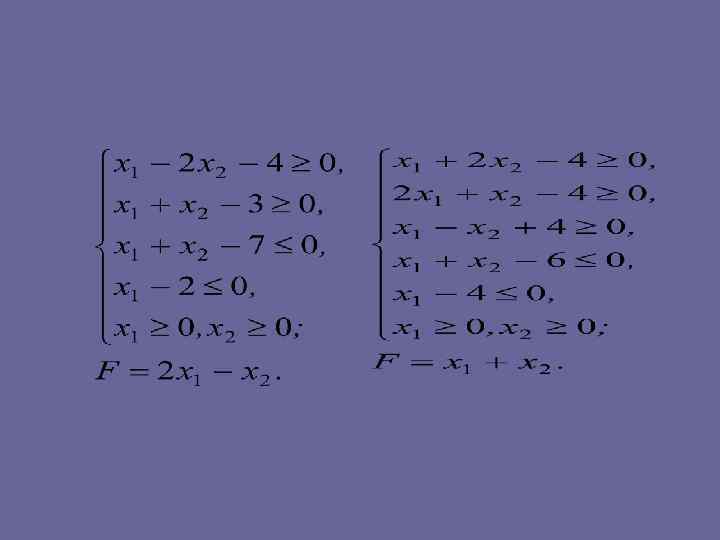
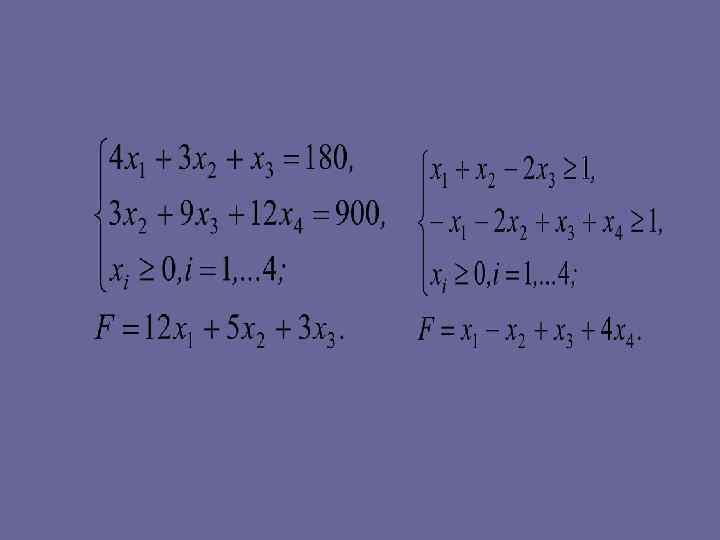
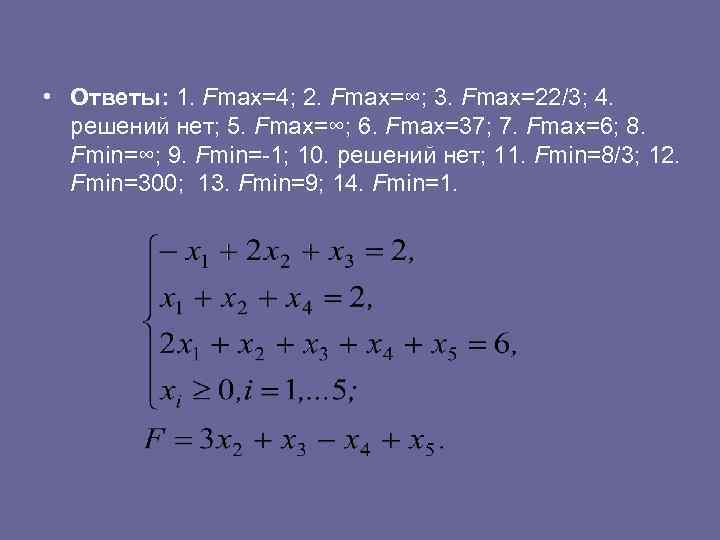
• Ответы: 1. Fmax=4; 2. Fmax=∞; 3. Fmax=22/3; 4. решений нет; 5. Fmax=∞; 6. Fmax=37; 7. Fmax=6; 8. Fmin=∞; 9. Fmin= 1; 10. решений нет; 11. Fmin=8/3; 12. Fmin=300; 13. Fmin=9; 14. Fmin=1.

3. ОСНОВНЫЕ ПОЛОЖЕНИЯ О РЕШЕНИИ ЗЛП • Утверждение 1. Решением системы ограничений ЗЛП (если он совместна) является выпуклый многогранник (на плоскости многоугольник). • Утверждение 2. Целевая функция достигает оптимальное решение хотя бы в одной угловой точке многогранника решений (если он ограниченный). • Утверждение 3. Если многогранник решений неограничен в направлении градиента целевой функции, то fmax = +∞, если в противоположном направлении, то fmin = -∞. • Утверждение 4. Точка X является угловой точкой многогранника тогда и только тогда, когда она является базисным решением системы ограничений ЗЛП.

• Из четвертого утверждения следует, что для решения ЗЛП можно простым перебором из всех базисных решений выбрать то, в котором целевая функция принимает наибольшее или наименьшее значение. Это и будет решением задачи. Любая система уравнений имеет конечное число базисных решений, равное , где n — число неизвестных, r — ранг системы векторов условий, но с ростом n число базисных решений резко растет. Так, например, если n = 8, a r = 3, то число базисных решений N≤ = 56. • Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются так называемыми опорными. Опорным решением задачи линейного программирования называется Х=( х10 , х20 , …, хт0 , 0, …, 0), для которого векторы условий, соответствующие положительным координатам А 1, А 2, . . . , Ат, линейно независимы.

• Число отличных от нуля координат опорного решения не может быть больше ранга r системы векторов условий (т. е. числа линейно независимых уравнений системы ограничений). В дальнейшем будем считать, что система ограничений состоит из линейно независимых уравнений, т. е. т = r. • Если число отличных от нуля координат опорного решения равно т, то оно (решение) называется невырожденным, в противном случае (меньше т) — вырожденным. • Базисом опорного решения называется базис системы векторов условий задачи, в состав которого входят векторы, соответствующие отличным от нуля координатам опорного решения.

Теоремы о взаимосвязи опорных решений и угловых точек области допустимых решений • Теорема 3. 1. Любое опорное решение является точкой области допустимых решений. • Доказательство. Пусть Х=( х10 , х20 , …, хт0 , 0, …, 0)— опорное решение с базисом Б = (A 1, А 2, . . . , Ат ) некоторой задачи с системой ограничений А 1 х1+А 2 х2 +. . . +Аn хn=А 0. Предположим, что X не является угловой точкой, тогда решение представляет собой выпуклую линейную комбинацию каких либо точек области допустимых решений, не совпадающих с X, например X' и X", т. е. Х=λ 1 Х'+λ 2 Х", λ 1 > 0, λ 2 > 0, λ 1 + λ 2= 1.

• Так как последние n - т координат вектора X равны нулю, а λ 1 и λ 2 положительные, то последние n-т координат векторов X' и X" также равны нулю, т. е. Х'= (х'1, х'2 , . . . , х'т, 0, . . . , 0) и Х"= (х"1, х"2, . . . , х"т, 0, . . . , 0). • Подставим X', X" в систему ограничений: • А 1 х´ 1 + А 2 х´ 2 +. . . + Ат хт´ = А 0 , • А 1 х´´ 1 + А 2 х´´ 2 +. . . + Ат хт´´= А 0. • Вычтем из первого равенства второе. Получим • А 1 (х´ 1 х´´ 1 )+ А 2 (х´ 2 х´´ 2) +. . . + Ат (хт´- хт´´)= θ. • Так как векторы А 1, А 2, . . . , Ат образуют базис, то они линейно независимы, а потому данное равенство может выполняться только тогда, когда все коэффициенты при векторах равны нулю, т. е. х´ 1 х´´ 1=0, х´ 2 х´´ 2=0, . . . , хт´- хт´´=0.

• Отсюда получаем, что х´ 1 = х´´ 1, х´ 2 = х´´ 2, . . . , хт´= хт´´. Следовательно, X'=X" и опорное решение X является не выпуклой линейной комбинацией каких либо точек области допустимых решений, а угловой точкой этой области. Ч. т. д. • Теорема 3. 2. Любая угловая точка области допустимых решений является опорным решением. • Доказательство. Пусть Х= (х1, х2, . . . , хт, 0, . . . , 0) угловая точка области допустимых решений, а хj > 0 для любого j = 1, 2, . . . , т. Чтобы доказать, что это решение является опорным, достаточно показать, что векторы А 1 , А 2, . . . , Ат , соответствующие положительным координатам решения, линейно независимы.

• Предположим, что эти векторы линейно зависимы. Тогда существует ненулевой набор чисел l 1, l 2, . . . , lm, такой, что А 1 l 1+ А 2 l 2 +. . . + Am lm =θ. (3. 1) • Так как X ― допустимое решение, то А 1 х1 + А 2 х2 +. . . + Аnхn = А 0. (3. 2) • Умножим соотношение (3. 1) на некоторое число ε и прибавим к равенству (3. 2), получим А 1 (х1 + l 1ε )+ А 2 (х2+ l 2 ε) +. . . + Ат (хт+ lm ε)= А 0 , вектор Х'= (х1 + l 1ε, х2+ l 2ε, …, хт+ l mε, 0, …, 0) является решением системы ограничений задачи. Аналогично можно показать, что решением системы является также вектор X" =( х1 l 1ε, х2 l 2 ε, …, хт- lm ε, 0, . . . , 0). • Для того чтобы векторы X ´ и X" удовлетворяли условиям неотрицательности, выберем достаточно малое число ε так, что х j ± l j ε > 0 при любых j. Эго возможно, так как х j > 0 при любых j = 1, 2, . . . , т.

• При таком выборе числа ε векторы X' и X" являются допустимыми решениями. Нетрудно видеть, что X = =, т. е. X представляет собой выпуклую линейную комбинацию X' и X". Это противоречит тому, что Х является угловой точкой. Следовательно, векторы А 1 , А 2, . . . , Ат линейно независимы и решение Х является опорным. Ч. т. д.

4. СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ • 4. 1. Симплекс-метод • Симплексный метод — это метод целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить, что оптимального решения не существует. • Идея симплексного метода состоит в следующем. Используя систему ограничений, приведенную к общему виду, т. е. к системе т линейных уравнений с n переменными (т < n), находят ее любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению

• Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему (в случае перехода к вырожденному базисному решению значение линейной формы не изменится). С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным. • Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляют переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком то шаге не получится допустимое базисное решение. После этого к нему применяют механизм симплексного метода, изложенный выше.

• Метод называется симплексным, так как области допустимых решений задач, которые рассматривались на начальном этапе развития метода, имели простейший (simple) вид. • Задача 1. Для изготовления шкафов и буфетов деревоотделочный завод применяет древесину четырех видов. Запасы древесины по каждому виду ограничены и составляют соответственно 120, 160, 120, 80 ед. Количество единиц древесины каждого вида, необходимое для изготовления одного шкафа и одного буфета, а также прибыль, получаемая заводом от реализации единицы продукции, даны в табл. 4. 1. • Требуется составить такой план выпуска продукции, который бы обеспечил предприятию наибольшую прибыль от реализации всей продукции.
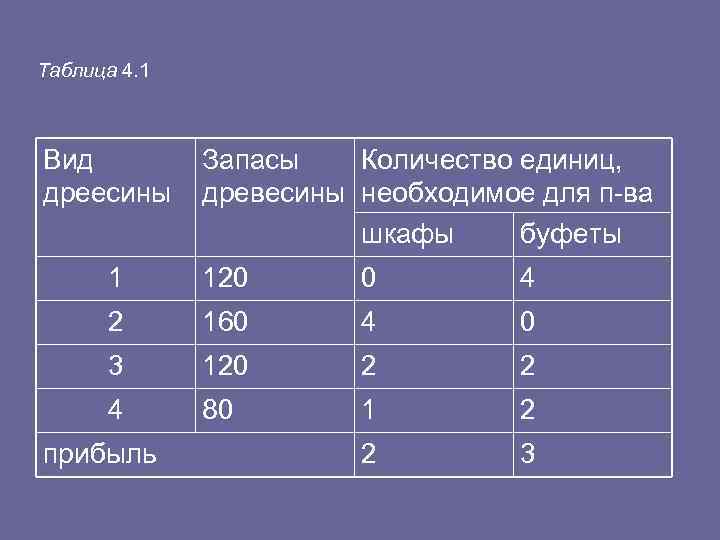
Таблица 4. 1 Вид Запасы Количество единиц, дреесины древесины необходимое для п ва шкафы буфеты 1 120 0 4 2 160 4 0 3 120 2 4 80 1 2 прибыль 2 3

• Решение. Дадим математическую формулировку задачи. Пусть х1 и х2 — количество шкафов и буфетов, запланированных к производству. • Так количество древесины по каждому виду ограничено, то должны выполняться следующие неравенства:

• Эта система неравенств и является системой ограничений данной задачи. Целевая функция (линейная форма), выражающая прибыль предприятия, имеет вид F = 2 х1 + 3 х2. • Итак, задача сводится к нахождению максимума функции F = 2 х1 + 3 х2 при ограничениях

• Для сведения системы ограничений неравенств к системе уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные х3 , х4, х5, х6. В условиях данной задачи они имеют конкретное экономическое содержание, а именно выражают объем остатков древесины каждого вида после выполнения плана по выпуску продукции. После введения добавочных переменных получим систему уравнений

• Нужно найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало линейную форму F = 2 х1 + 3 х2. • Так как система ограничений есть система четырех независимых уравнений с шестью переменными, то число базисных переменных должно равняться четырем, а число свободных — двум. • Для решения задачи симплексным методом прежде всего нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаточно взять в качестве базисных добавочные переменные х3 , х4, х5, х6. Так коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель.

• Считая свободными переменные х1 и х2 равными нулю, получим базисное решение (0; 0; 120; 160; 120; 80), которое к тому же оказалось допустимым. Поэтому здесь отпадает надобность в применении первого этапа симплексного метода. Переходим сразу ко второму этапу, т. е. к поискам оптимального решения. • I ш а г. Базисные переменные: х3 , х4, х5, х6; свободные переменные: х1, х2. В системе (4. 1) базисные переменные выразим через свободные. Для того чтобы судить, оставить ли свободные переменные в числе свободных или их выгоднее с точки зрения приближения к оптимальному решению перевести в базисные, следует выразить через них и линейную форму (в данном случае она уже выражена через переменные х1 и х2).

• Тогда получим F = 2 х1 + 3 х2. При x 1 = х2 = 0 имеем х3 = 120, х4 = 160, x 5 = 120, х6 = 80, что дает базисное решение (0; 0; 120; 160; 120; 80), которое мы приняли за исходное. При этом базисном решении значение линейной формы F =2 х1 + 3 х2 = 0.

• Когда мы полагали x 1 = х2 = 0 (завод ничего не выпускает), была поставлена цель — найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого первоначального решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных х1 и х2. Иными словами, эти переменные невыгодно считать свободными, т. е. равными нулю, их нужно перевести в число базисных. Это и означает переход к новому базисному решению. При симплексном методе на каждом шаге решения предполагается перевод в число базисных только одной из свободных переменных. Переведем в число базисных переменную х2, так как она входит в выражение линейной формы с большим коэффициентом.

• Как только одна из свободных переменных переходит в число базисных, одна из базисных должна быть переведена на ее место в число свободных. Какую же из четырех базисных переменных нужно вывести? Ответить на этот вопрос помогут следующие рассуждения. • Значение х2 необходимо сделать как можно большим, так как это соответствует конечной цели — максимизации F. Однако оказывается, что увеличение х2 может продолжаться только до известных границ, а именно до тех пор, пока не нарушится требование неотрицательности переменных.

• Так, из первого уравнения системы (4. 2) следует, что переменная х2 не должна превышать числа 120/4, т. е. х2 ≤ 30, поскольку только при этих значениях х2 переменная х3 остается положительной (если х2 = 30, то х3 = 0; если же х2 >30, то х3 < 0). Из третьего уравнения системы (4. 2) следует, что х2 ≤ 120/2, т. е. х2 ≤ 60, из четвертого — что х2 ≤ 80/2, т. е. х2 ≤ 40 (во второе уравнение переменная х2 не входит). Всем этим условиям удовлетворяет х2 ≤ 30. • Иными словами, для ответа на вопрос, какую переменную нужно перевести в число свободных, нужно принять х2= min {120/4; 120/2; 80/2} = min {30; 60; 40} = 30. Тогда х3= 0 и х3 переходит в число свободных переменных, a x 4 и х5 останутся положительными.

• II ш а г. Базисные переменные: х2, x 4, х5, х6; свободные переменные: х1 , х3. Выразим базисные переменные и линейную форму через свободные. В системе (4. 2) берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при х2. В данном случае это первое уравнение, которое выделено рамкой. Выразив из этого уравнения х2, имеем х2= 30 — 0, 25 х3. Подставим это выражение х2 во все остальные уравнения системы (4. 2) и в линейную форму F и, приведя подобные члены, получим

• Подставим это выражение х2 во все остальные уравнения системы (4. 2) и в линейную форму F и, приведя подобные члены, получим F = 90+2 х1 0, 75 х3. При x 1 = х3 = 0 имеем F = 90. Это уже лучше, чем на I шаге, но не искомый максимум. Дальнейшее увеличение функции F возможно за счет введения переменной х1 в число базисных; так как эта переменная входит в выражение F с положительным коэффициентом, поэтому ее увеличение приводит к увеличению линейной формы и ее невыгодно считать свободной, т. е. равной нулю.

• Для ответа на вопрос, какую переменную вывести из базисных в свободные, примем х1 = min {160/4; 60/2; 20/1} = 20. Тогда х6 =0 и х6 переходит в число свободных переменных, a x 4 и х5 остаются при этом положительными. • Первое уравнение не используется при нахождении указанного минимума, так как х1 не входит в это уравнение. • III шаг. Базисные переменные: х1, х2, x 4, х5; свободные переменные: x 3, х6. Выразим основные переменные и линейную форму через свободные. Из последнего уравнения системы (4. 3) (выделено) имеем х1= 20 + 0, 5 х3 — х6.

• Подставляя это выражение в остальные уравнения и в линейную форму, получим: F = 130+0, 25 х3 2 х6. Из выражения линейной формы следует, что ее максимальное значение еще не получено, так как возможно увеличение F за счет введения в базисные переменной х3 (она имеет положительный коэффициент). Полагаем х3 = min {∞; 30/0, 25; 80/2; 20/0, 5} = 40.

• Во первых, хотя переменная х3 и входит в выражение для х1 [первое уравнение системы (4. 4)], но имеет положительный коэффициент и при любом возрастании х3 переменная х1 не может стать отрицательной. Иными словами, в первом уравнении никаких ограничений на возрастание переменной х3 не накладывается, поэтому мы условно пишем ∞. Условимся в дальнейшем пользоваться этим же обозначением, если переменная, вновь вводимая в число базисных, не входит в какое либо уравнение системы ограничений. Во вторых, мы получим два одинаковых минимальных значения, равные 40. Если х3 = 40, то х4= 0 и х5 = 0, т. е. напрашивается вывод, что вместо одной переменной нужно перевести в число свободных сразу две: х4 и х5.

• Но число базисных переменных не должно быть меньше четырех. Поэтому одну из переменных (x 4 или х5) оставляют в числе основных, но при этом ее значение считают равным нулю, т. е. полученное на следующем шаге базисное решение оказывается вырожденным. Оставим, например, x 4 в числе базисных переменных, а х5 переведем в число свободных. • IV шаг. Базисные переменные: x 1, x 2, x 3, x 4; свободные переменные: х5, х6. Выразим базисные переменные и линейную форму F через свободные, начав это выражение из четвертого уравнения системы (4. 4).
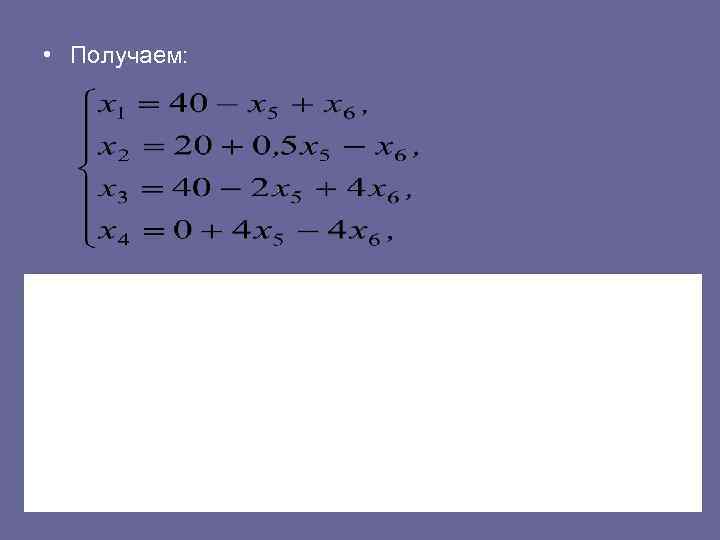
• Получаем: F = 140 0, 5 х5 х6. Так как в выражение линейной формы переменные х5 и х6 входят с отрицательным коэффициентами, то никакое увеличение F за счет этих переменных невозможно. Отсутствие на каком-то шаге симплексного метода в выражении линейной формы F, максимум которой ищется, неосновных переменных с положительными коэффициентами является критерием оптимальности.

• Следовательно, на IV шаге критерий оптимальности достигнут и задача решена. Оптимальным служит решение (40; 20; 40; 0; 0; 0), при котором Fmаx= 140. Таким образом, для получения наибольшей прибыли, равной 140 ден. ед. , из данных запасов древесины завод должен изготовить 40 шкафов и 20 буфетов. При этом древесина II, III и IV видов окажется использованной полностью, а 40 ед. древесины I вида останутся неизрасходованными. • Задача 2. На свиноферме производится откорм свиней. Известно, что каждая свинья должна ежедневно получать не менее 6 ед. вещества К, 8 ед. вещества L и 12 ед. вещества М (вещества К, L, М могут, в частности, означать жиры, белки и углеводы). Для откорма свиней можно закупить три вида кормов: I, II и III (например, картофель, жмых и комбикорм). Содержание каждого вещества в различных видах корма и стоимость единицы каждого корма приведены в табл. 4. 2. Требуется обеспечить наиболее дешевый рацион откорма. •
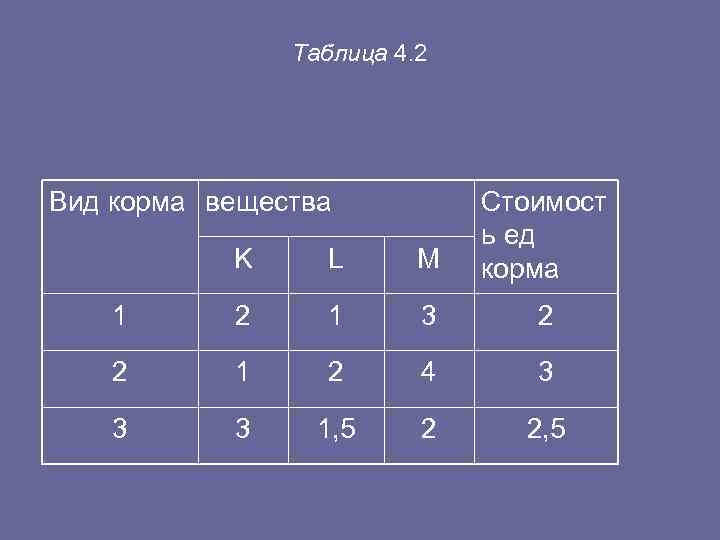
Таблица 4. 2 Вид корма вещества Стоимост ь ед K L M корма 1 2 1 3 2 2 1 2 4 3 3 3 1, 5 2 2, 5

• Решение. Составим экономико математическую модель задачи. Пусть х1, х2 и х3, — количество единиц соответственно I, II и III видов корма. Требуется найти минимум линейной формы F = 2 х1+3 х2+2, 5 х3 при следующих ограничениях:

• Введя добавочные неотрицательные переменные x 1, х2 и х3, сведем систему неравенств к системе уравнений Проще всего получить базисное решение последней системы, если за базисные взять добавочные переменные х 4 , х 5 и x 6. Правда, базисное решение (0, 0; 0; 6; 8; 12), в котором эти переменные являются базисными, — недопустимое.

Поэтому сначала воспользуемся симплексным методом для перехода к какому либо допустимому базисному решению, Переведем в базисные переменную х 1. Для этого положим х 1 = min {3; 8; 4}=3. При х 1 = 3 имеем x 4 =0 и x 4 переходит в свободные переменные.
Линейно программирование.ppt