7 Корреляционно-регрессионный анализ.ppt
- Количество слайдов: 24

ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ ТЕМА: КОРРЕЛЯЦИОННОРЕГРЕССИОННЫЙ АНАЛИЗ

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Корреляционная зависимость это взаимосвязь между признаками, состоящая в том, что в зависимости от изменения факторного признака меняется средняя величина значений результативных признаков В основе корреляционного анализа лежит представление о типе, форме и тесноте (плотности) как свойстве связи

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Классификация корреляционных связей: 1. По типу: 1. 1 прямые 1. 2 обратные 2. По форме: 2. 1 прямолинейные (линейные): yx = a 0+a 1 x 2. 2 криволинейные (нелинейные): 2. 2. 1 параболы второго порядка (или высших порядков): yx = a 0+a 1 x+a 2 x 2 2. 2. 2 гиперболы yx = a 0+a 1/x 2. 2. 3 показательные функции: yx = a 0 a 1 x и т. д.
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Корреляция Парная: выявляет тип, форму и плотность связи между двумя признаками Множественная: выявляет взаимосвязь между несколькими признаками

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Теснота (плотность) связи - это степень сопряженности между двумя явлениями, признаками, величинами Связь считается более тесной в том случае, когда каждому значению одного признака соответствуют близкие другу, тесно расположенные около своей средней величины значения другого признака. Связь считается менее тесной, если эти значения сильно отклоняются от своей средней.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Пример построения корреляционного поля и определения формы связи Исследование зависимости между среднемесячными доходами X на семью (в тыс. у. е. ) и расходами Y на покупку кондитерских изделий (в у. е. ) представлено в таблице: x 4, 8 3, 8 5, 4 4, 2 3, 4 4, 6 3, 4 4, 8 5, 0 3, 8 5, 2 4, 0 3, 8 4, 6 4, 4 y 75 68 78 71 64 73 66 75 75 65 77 69 67 72 70 Построить корреляционное поле и сделать предварительный вывод о форме зависимости случайных величин.
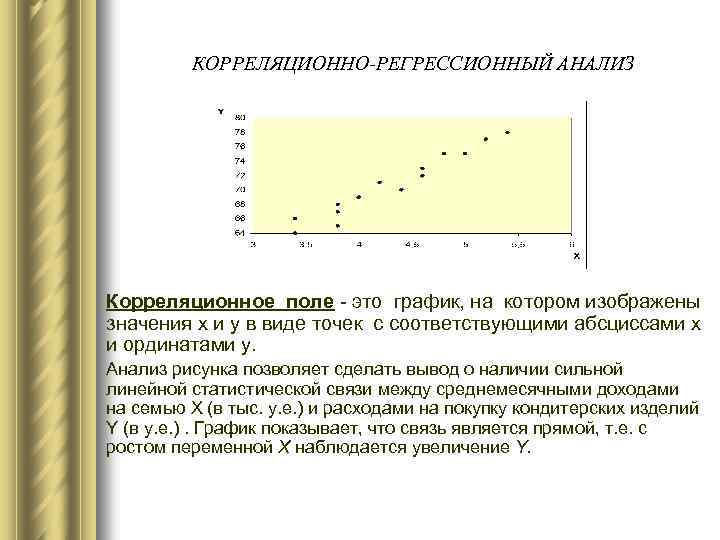
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Корреляционное поле - это график, на котором изображены значения х и у в виде точек с соответствующими абсциссами х и ординатами у. Анализ рисунка позволяет сделать вывод о наличии сильной линейной статистической связи между среднемесячными доходами на семью X (в тыс. у. е. ) и расходами на покупку кондитерских изделий Y (в у. е. ). График показывает, что связь является прямой, т. е. с ростом переменной X наблюдается увеличение Y.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Коэффициент корреляции - мера тесноты связи при линейной корреляции r = (х - х) * (y - у) / n* x * y где (х - х) / x - нормированное отклонение признака x (y - у) / y - нормированное отклонение признака у x и y - средние квадратические отклонения признаков х и у n - число наблюдений -1 <r<1: Знак «+» - прямая зависимость Знак «-» - обратная зависимость r = 0 отсутствие линейной связи

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Шкала Чеддока r 0, 1 -0, 3 -0, 5 -0, 7 -0, 9 Слабая Умеренная Заметная Сильная 0, 9 -0, 99 Очень сильная

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ Если значение коэффициента корреляции близко к 0 возможно между фактором и результативным признаком существует криволинейная форма связи, которая не улавливается коэффициентом корреляции y / x = ( yx ) / y ; x /y = ( xy ) / x ( yx ) – среднее квадратическое отклонение под влиянием только х. Связь считается нелинейной, когда r. Если L= 2_r 2 и L>0, то связь криволинейна. Если L=0, то связь прямолинейна.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Уравнения регрессии – уравнения линии регрессии относительно осей координат Ох и Оу Регрессия – среднее изменение функции (результативного признака у) на единицу изменения аргумента (фактора х) В случае линейной зависимости уравнением парной регрессии является уравнение прямой у = а ± bх Построенный на основе этого уравнения график для конкретных данных называется линией регрессии. Корреляционное поле - это график, на котором изображены значения х и у в виде точек с соответствующими абсциссами х и ординатами у

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Коэффициент регрессии применяется для измерения изменений одной величины в соответствии с изменением другой R x / y = r * ( x / y ) ; R y / x = r * ( y / x ) где R x / y - коэффициент регрессии х на у (х от у); R y / x - коэффициент регрессии у на х (у от х); x - среднее квадратическое отклонение по признаку х; y - среднее квадратическое отклонение по признаку у; r - коэффициент корреляции

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Нахождение параметров уравнения

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Множественная корреляция Множественной называется такая корреляция, при которой результативный признак связан с несколькими факторными признаками Пример: уравнение множественной корреляции при связи результирующего и двух факторных признаков: yxz = a 0 ± a 1 x ± a 2 z Для нахождения неизвестных а 0, а 1, и а 2 способом наименьших квадратов составляется и решается следующая система нормальных уравнений: a 0 n + а 1 х + a 2 z = у; а 0 х + а 1 х2 + а 2 хz = ху; а 0 z + а 1 xz + a 2 z 2 = zу.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Множественная корреляция При линейной форме множественной корреляции теснота связи между результативным (у) и двумя факторными (х и z) признаками измеряется с помощью совокупного (множественного) коэффициента корреляции: R yxz = ( r 2 yx + r 2 yz 2 ryx * ryz * rxz ) / 1 r 2 xz где ryx, ryz и rxz - линейные коэффициенты парной корреляции между соответствующими признаками

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ l

Макроэкономическая модель социально экономического развития Калининградской области GRP = 0, 8429 INV - 0, 0137 REVTAX + 2, 1396 GDP 1, 5703 FTT + 1, 9693 IND + 10, 0619 + error term Где: Валовый региональный продукт (GRP) l Инвестиции в основной капитал (INV). l Доходы регионального бюджета (REVTAX). l Валовой внутренний продукт РФ (GDP). l Внешнеторговый оборот Калининградской области (FTT). l Объем производства промышленной продукции (IND).

Макроэкономическая модель социально экономического развития Калининградской области INV = 0, 9892 INVFED*0, 9971 IND*1, 0022 BAL* 1, 0018 INTRATE * 1, 0119 INVREG*43, 58* error term Где: ИНВЕСТИЦИИ В ОСНОВНОЙ КАПИТАЛ (INV). l Федеральные инвестиции (INVFED). l Объем производства промышленной продукции (IND). l Сальдированный финансовый результат предприятий (BAL). l Процентная ставка кредита (INTRATE). l Инвестиции консолидированного бюджета области (INVREG).

Макроэкономическая модель социально экономического развития Калининградской области REVTAX = -6, 4395 TAXLEV -0, 1815 REVPOP + 0, 3447 BAL+ 0, 2984 UNEMP – 442, 784 OILPR+234, 31 + error term Где: ДОХОДЫ РЕГИОНАЛЬНОГО БЮДЖЕТА (REVTAX) l Уровень налоговых изъятий (TAXLEV). l Общие доходы населения (REVPOP). l Сальдированный финансовый результат предприятий (BAL). l Численность безработных (UNEMP). l Цена нефти Брент средняя, US$ FOB (EIA) (OILPR).
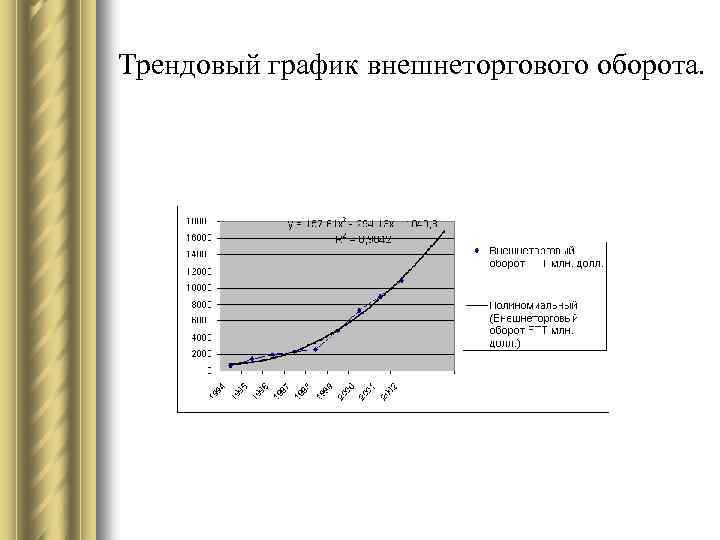
Трендовый график внешнеторгового оборота.
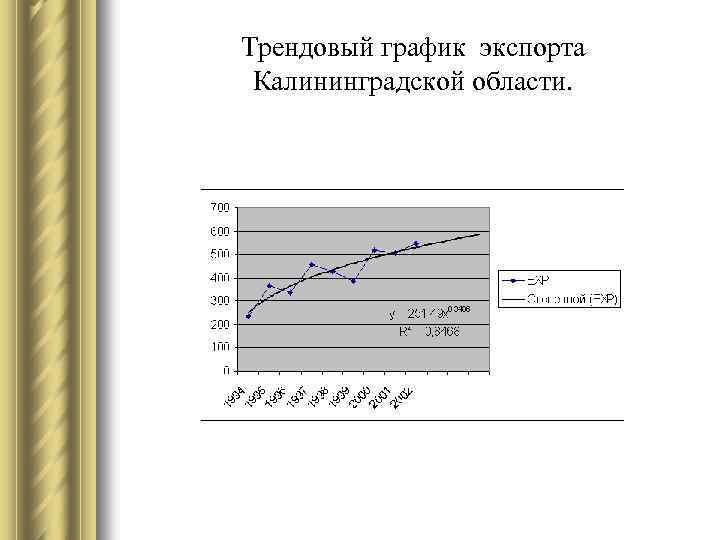
Трендовый график экспорта Калининградской области.
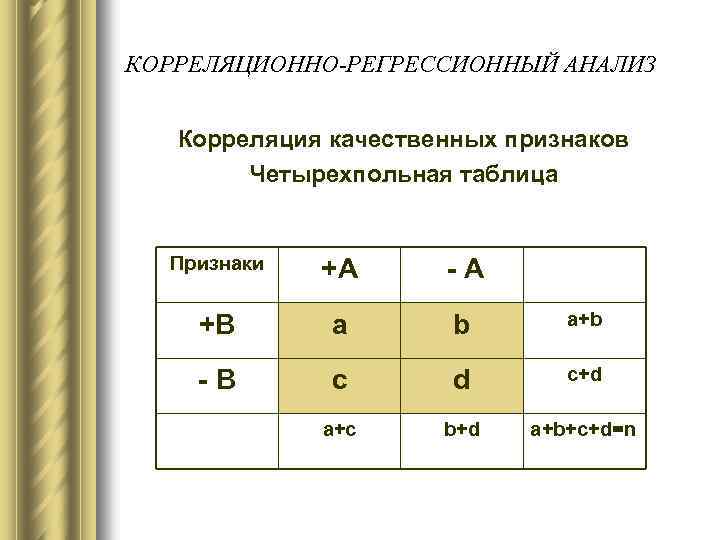
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Корреляция качественных признаков Четырехпольная таблица Признаки +А - А +В a b a+b - В c d c+d a+c b+d a+b+c+d=n

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Коэффициент связи Коэффициент сопряженности
7 Корреляционно-регрессионный анализ.ppt