Общая физика. Раздел «Элементы релятивистской механики» 1 Кафедра

Общая физика. Раздел «Элементы релятивистской механики» 1 Кафедра физики 1. Принцип относительности Галилея в классической механике. 2. Принцип относительности Эйнштейна. 3. Преобразования Лоренца. 4. Некоторые следствия из преобразований Лоренца. Элементы релятивистско й й механики ЛЕКЦИЯ 4 4 , часть 1. План лекции

Общая физика. Раздел «Элементы релятивистской механики» 2 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ ПП ринцип относительности Галилея (сведения из классической механики) Л юбое механическое явление протекает одинаково во всех инерциальных системах отсчета. Никакими механическими опытами, проводимыми в инерциальной системе отсчета, нельзя установить, движется эта ли эта система отсчета прямолинейно и равномерно, или покоится. Принципу относительности Галилея соответствуют преобразования координат Галилея. Преобразования Галилея позволяют по известным координатам и времени некоторого события в одной инерциальной системе отсчета, найти координаты и время этого же события в другой инерциальной системе, движущейся относительно первой с некоторой скоростью . . V

Общая физика. Раздел «Элементы релятивистской механики» 3 Кафедра физики z*Vt*хх * yy * zz * tt 0* 0 z* xy y* x*К К * V Vtх * хy * yz * zt * t Прямые преобразования Галилея : Обратные преобразования Галилея : ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ ПП ринцип относительности Галилея (сведения из классической механики)

Общая физика. Раздел «Элементы релятивистской механики» 4 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ Уравнения классической механики (например законы Ньютона) инвариантны или одинаковы относительно преобразований. Среди основных инвариантов классической механики можно особо выделить пространственный интервал (расстояние между двумя пространственными точками) и временной интервал . 12 l *tt. Физические величины, которые при преобразованиях Галилея остаются неизменными, называются инвариантами Галилея. Принцип относительности и преобразования Галилея отражают представления об абсолютном пространстве и абсолютном времени, которые лежат в основе классической механики. С точки зрения классической механики время абсолютно и во всех системах отсчета течет одинаково. ПП ринцип относительности Галилея (сведения из классической механики)

Общая физика. Раздел «Элементы релятивистской механики» 5 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ ПП ринцип относительности Эйнштейна Главные идеи специальной теории относительности: 1. Все физические явления (не только механические) в инерциальных системах протекают одинаково. Это сформулированный в общем виде принцип относительности Эйнштейна. 2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от источников и приемников света, т. е. является универсальной постоянной. Скорость света в вакууме равна 2, 99793*10 8 м/с

Общая физика. Раздел «Элементы релятивистской механики» 6 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ Скорость света в вакууме не только универсальная постоянная. Это максимально возможная скорость движения в природе. Никакой сигнал, никакое воздействие одного тела на другое не может распространяться со скоростью, большей скорости света в вакууме. Итак, в основе специальной теории относительности лежат два постулата: обобщенный принцип относительности и принцип постоянства скорости света в вакууме. Принцип относительности Эйнштейна

Общая физика. Раздел «Элементы релятивистской механики» 7 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ Найдем преобразования для x и t. Преобразования Лоренца)tvγ(xx * 0 * где — константа. γ t)vγ(xx 0 * Вследствие равноправности систем отсчета величина коэффициент γ не должен изменяться при переходе от К к К * и наоборот. z о* о z* xy y* x*К К * v

Общая физика. Раздел «Элементы релятивистской механики» 8 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ Система К* движется относительно неподвижной системы K со скоростью v 0 . )tvγ(xx * 0 * t)vγ(xx 0 * Пусть в момент времени t * = t =0 начала координат систем К и К* совпадают. ctx В этот момент времени t * = t =0 в направлении осей х * и х направляется световой сигнал, который производит вспышку на экране. Это событие характеризуется в системе К координатой х и моментом времени t , а в системе К * координатой х * и моментом времени t * : ** ctx. Преобразования Лоренца

Общая физика. Раздел «Элементы релятивистской механики» 9 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ 22 0 cv 1 1 γ *2 0 22*2 tt)v(cγttc Подставим в формулы преобразования, получим * 0 * t)vγ(c)tvγ(ctct t)vγ(ctct 00 * Перемножим соотношения )v(cγc 2 0 222 Преобразования Лоренца

Общая физика. Раздел «Элементы релятивистской механики» 10 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ 22 0 * cv 1 tvx x 22 0 * cv 1 x)/c(vt t Подставим соотношение для γ в формулы преобразования 22 0 0* cv 1 tvx x Исключим из полученных соотношений х и разрешим их для t. Преобразования Лоренца

Общая физика. Раздел «Элементы релятивистской механики» 11 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ В итоге имеем совокупность формул, получивших название преобразований Лоренца: 2 ** β 1 tcβx x * yy * zz 2 ** 1 x)c/(t t c v β 0 Обозначим. Преобразования Лоренца

Общая физика. Раздел «Элементы релятивистской механики» 12 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ Обратные преобразования Лоренца: 2 * β 1 tcβx x yy * zz * 2 * 1 x)c/(t t По приведенным формулам производится обратный переход от системы отсчета к системе . * K K ФИЗИЧЕСКИЕ ЗАКОНЫ ИНВАРИАНТНЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА еще одна формулировка принципа относительности. Преобразования Лоренца

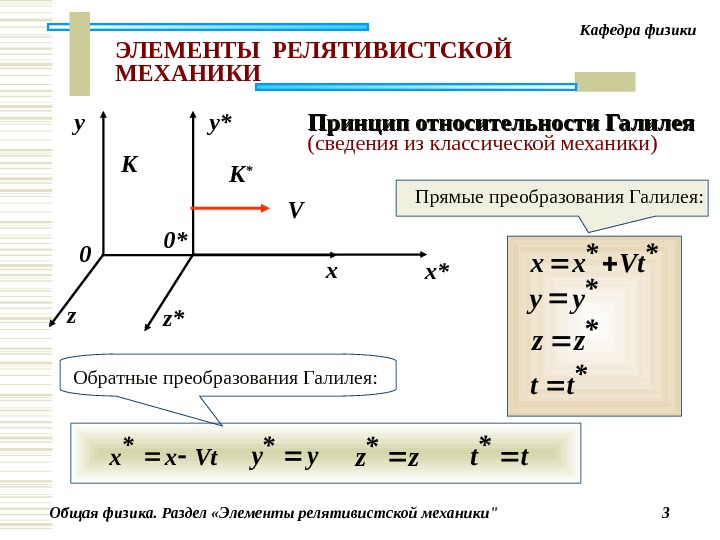
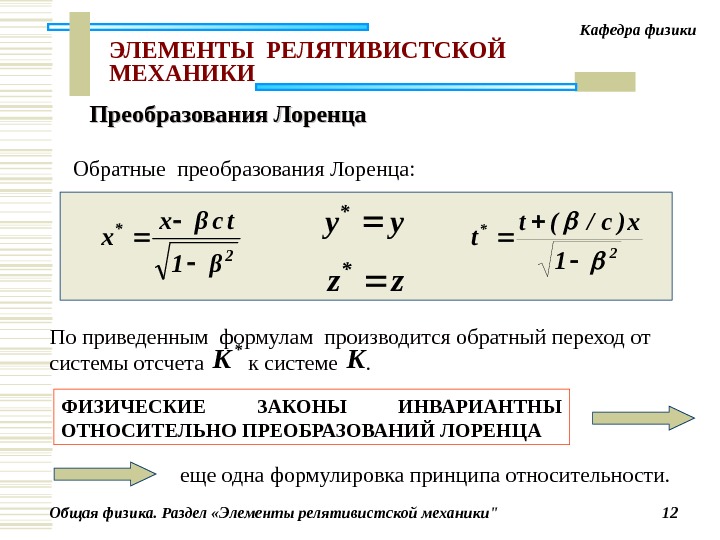
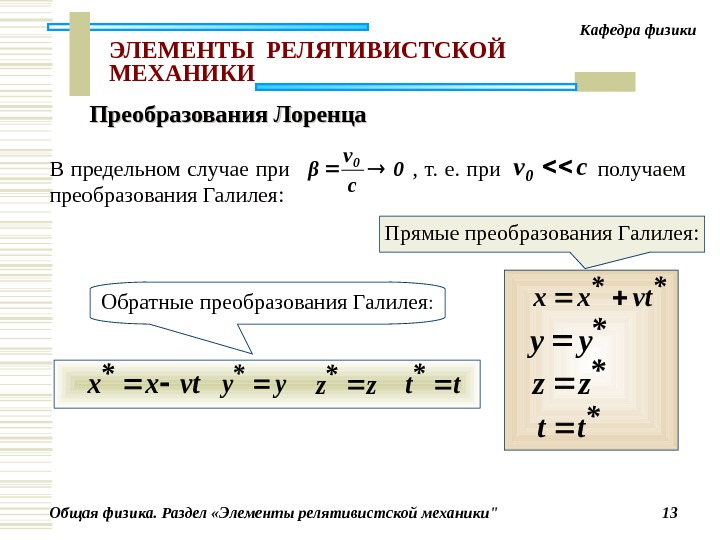
Общая физика. Раздел «Элементы релятивистской механики» 13 Кафедра физики ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКО Й МЕХАНИКИ В предельном случае при , т. е. при получаем преобразования Галилея: 0 c v β 0 cv 0 * vt * хх * yy * zz * tt Прямые преобразования Галилея : vtх * хy * yz * zt * t Обратные преобразования Галилея : Преобразования Лоренца