ОБС 9 ОСНОВЫ БИОСТАТИСТИКИ

ОБС 9 ОСНОВЫ БИОСТАТИСТИКИ СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ http: //www. hydrobiology. spb. ru ОБС 1 ОБС 2 ОБС 3 БИБЛИОТЕКА ОБС 4 ОБС 5 ОБС 6 ОБС 7 ОБС 8 ОБС 9

ОБС 9 ОСНОВЫ БИОСТАТИСТИКИ http: //www. hydrobiology. spb. ru БИБЛИОТЕКА Biostat-1 Biostat-2 Biostat-3 Biostat-4 Biostat-5 Biostat-6 Biostat-7 Biostat-8 Biostat-9 Фото: Risto Vainola

ЭКЗАМЕН Можно: 1. Принести мат- рикул и получить в ? 7 нём оценку предвательного 5 тестирования 8 2. Отдать матрикул 6 старосте группы и мы проставим там оценку предварительного 1 2 3 тестирования До сессии будут организованы два предварительных теста, 3. Сдать тест с итоги которых будут учтены при экзаменационной аттестации обнулением ? итогов предвари- 1 этап. Тест по группам на последнем занятии, или в зачетную тельного неделю ( в часы занятий данной группы) + анкетирование. тестирования 2 этап. Тест для всех студентов курса в зачетную неделю в 4. Попасть на часы лекции. 15 (? ) мая в 9 (? )часов пересдачу в конце 3 этап. Тест по группам в даты, обозначенные в расписании сентября экзаменов группы. Это оффициальный срок сдачи экзамена по биостатистике. Начало в 11 часов.

На практике часто получается, что: - вид распределения не известен или он заведомо отличается от нормального; - использование критерия хи-квадрат ограничено объемом выборки; - данные представляют из себя ранговые показатели. Статистики основанные на ранжированных величинах называют порядковыми. Статистики основанные на рангах называют ранговыми. Xi : 3 5 4 7 10 9 16 14 Ранг: 1 3 2 4 6 5 8 7

СРАВНЕНИЕ ВЫБОРОК (НЕПАРАМЕТРИЧЕСКОЕ ОЦЕНИВАНИЕ) Критерии: U-Вилкоксона Манна-Уитни Вандер Вардена T Уайда Колмогорова- Смирнова λ Лямбда Q Розенбаума КОБЗАРЬ А. И. ПРИКЛАДНАЯ МАТЕМАТИЧЕСКАЯ Серийный СТАТИСТИКА. ДЛЯ ИНЖЕНЕРОВ И Знаков НАУЧНЫХ РАБОТНИКОВ. Физматлит, 2006 г. 816 cтр. Медианы. . . .

Сравнительная мощность критериев при оценке нормальности распределений коэффициент эксцесса

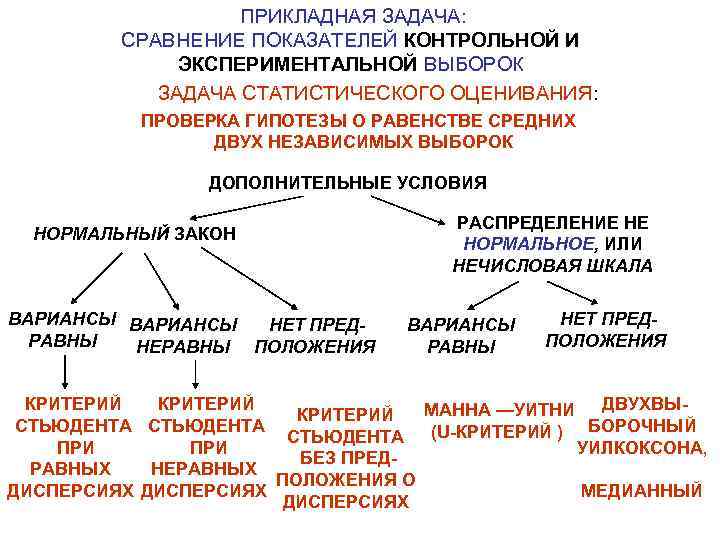
ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ ПОКАЗАТЕЛЕЙ КОНТРОЛЬНОЙ И ЭКСПЕРИМЕНТАЛЬНОЙ ВЫБОРОК ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНЫЙ ЗАКОН НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА ВАРИАНСЫ НЕТ ПРЕД- РАВНЫ НЕРАВНЫ ПОЛОЖЕНИЯ КРИТЕРИЙ МАННА —УИТНИ ДВУХВЫ- КРИТЕРИЙ СТЬЮДЕНТА БОРОЧНЫЙ СТЬЮДЕНТА (U-КРИТЕРИЙ ) ПРИ УИЛКОКСОНА, БЕЗ ПРЕД- РАВНЫХ НЕРАВНЫХ ПОЛОЖЕНИЯ О ДИСПЕРСИЯХ МЕДИАННЫЙ ДИСПЕРСИЯХ

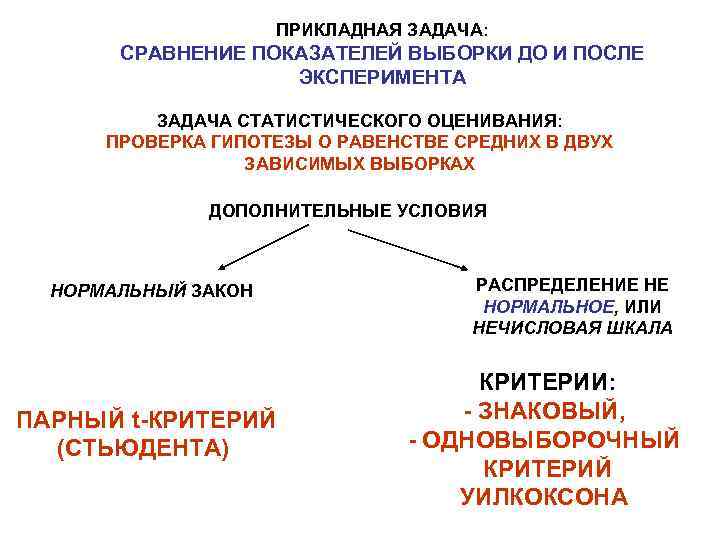
ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ ПОКАЗАТЕЛЕЙ ВЫБОРКИ ДО И ПОСЛЕ ЭКСПЕРИМЕНТА ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ В ДВУХ ЗАВИСИМЫХ ВЫБОРКАХ ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: ПАРНЫЙ t-КРИТЕРИЙ - ЗНАКОВЫЙ, (СТЬЮДЕНТА) - ОДНОВЫБОРОЧНЫЙ КРИТЕРИЙ УИЛКОКСОНА

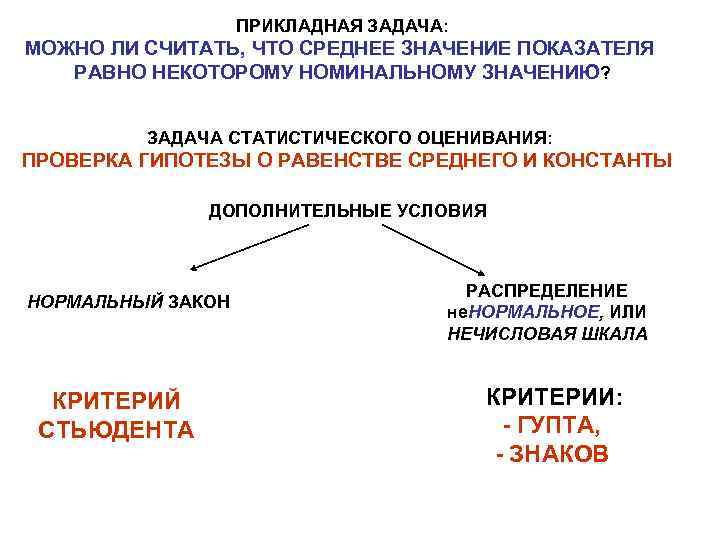
ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЯ РАВНО НЕКОТОРОМУ НОМИНАЛЬНОМУ ЗНАЧЕНИЮ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНЕГО И КОНСТАНТЫ ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ РАСПРЕДЕЛЕНИЕ НОРМАЛЬНЫЙ ЗАКОН не. НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИЙ КРИТЕРИИ: СТЬЮДЕНТА - ГУПТА, - ЗНАКОВ

ДАННЫЕ НЕЧИСЛОВЫЕ – …. широко распространены в социологии. Примеры нечисловых данных: - совокупность величин, полученных по шкалам; - частично упорядоченные множества (т. е. такие совокупности величин, для которых хотя и имеет смысл отношение порядка, но определено это отношение не для всех пар элементов совокупности); - графы (см. теория графов); - результаты ранжировок респондентами предлагаемых им объектов; - результаты попарного сравнения объектов; - разбиение множества объектов (т. е. представление его в виде системы подмножеств, не имеющих попарно общих точек); - и пр. …

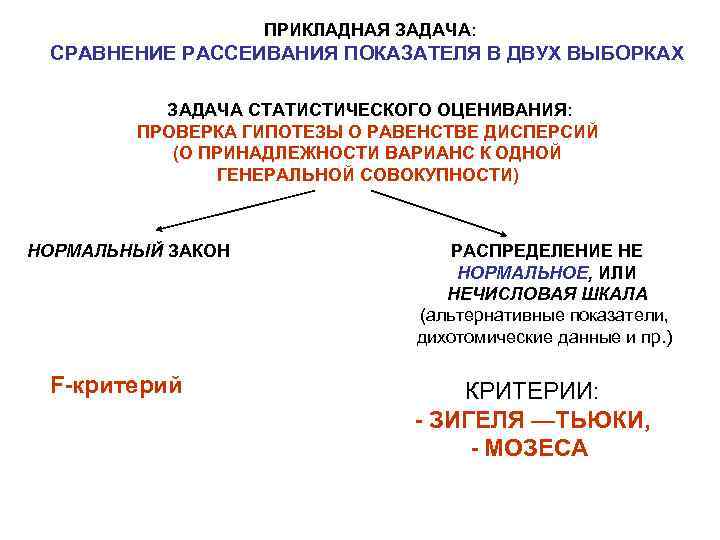
ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ РАССЕИВАНИЯ ПОКАЗАТЕЛЯ В ДВУХ ВЫБОРКАХ ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ (О ПРИНАДЛЕЖНОСТИ ВАРИАНС К ОДНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ) НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА (альтернативные показатели, дихотомические данные и пр. ) F-критерий КРИТЕРИИ: - ЗИГЕЛЯ —ТЬЮКИ, - МОЗЕСА

Работа с многомерными статистическими комплексами ni ni ДИСПЕРСИОННЫЙ АНАЛИЗ ni ni КОРРЕЛЯЦИОННЫЙ АНАЛИЗ способ наиболее эффективного позволяет изучать различия размещения объектов, между двумя и более РЕГРЕССИОННЫЙ АНАЛИЗ приближенно сохраняющий группами объектов по расстояния между ними в нескольким переменным КЛАСТЕРНЫЙ АНАЛИЗ новом пространстве признаков, одновременно метод, позволяющий ряд методов, используемых позволяет исследовать статистический метод размерность которого обнаружить зависимость ФАКТОРНЫЙ АНАЛИЗ для группировки объектов, различие между группами исследования зависимости существенно меньше исходного между несколькими событий или индивидов в данных случайной величины от случайными величинами. классы (кластеры) на основе одной или нескольких МЕТОД ГЛАВНЫХ КОМПОНЕНТ сходства их характерных переменных МЕТОД МНОГОМЕРНОГО признаков. один из основных способов многомерный метод, ШКАЛИРОВАНИЯ применяемый для изучения уменьшить размерность ДИСКРИМИНАНТНЫЙ АНАЛИЗ взаимосвязей между данных, потеряв значениями переменных, наименьшее количество для сокращения их числа. информации

МНОЖЕСТВЕННОЕ (m>2) СРАВНЕНИЕ ВЫБОРОК АНАЛИЗ СТАТИСТИЧЕСКИХ СВЯЗЕЙ ДИСПЕРСИОННЫЙ АНАЛИЗ (ANOVA) Ronald Aylmer Fisher George W. Snedecor 1890 - 1962 1882 -1974

A statistician's wife had twins. He was delighted. He rang the minister who was also delighted: «Bring them to church on Sunday and we'll baptize them» , said the minister. «No» , replied the statistician. «Baptize one. We'll keep the other as a control. »

Дисперсионный анализ основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты. Сравнивая их друг с другом с помощью F-критерия, можно определить, какую долю общей вариации изучаемого признака, обуславливает действие на него организованных и случайных воздействий. Основная идея дисперсионного анализа 1. Есть m- выборок, полученных из одной генеральной по определенному порядку - статистический комплекс. 2. В генеральной совокупности, из которой получены выборки, любое отдельное наблюдение рассматривается как единичная реализация случайной величины

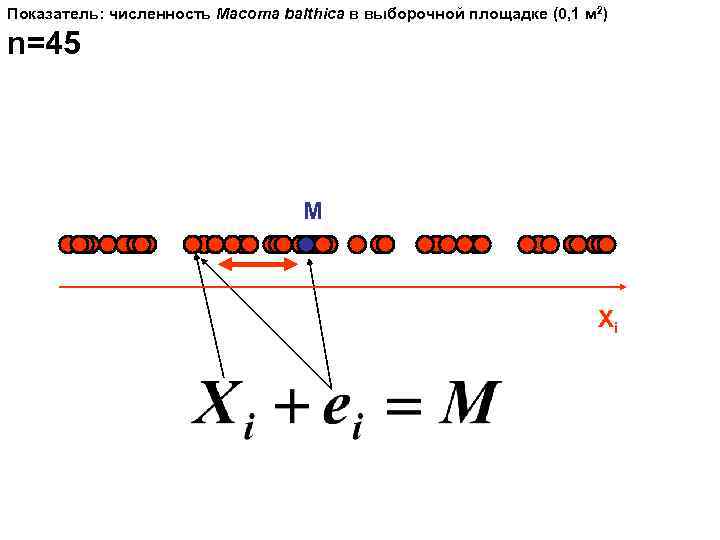
Показатель: численность Macoma balthica в выборочной площадке (0, 1 м 2) n=45 M Xi

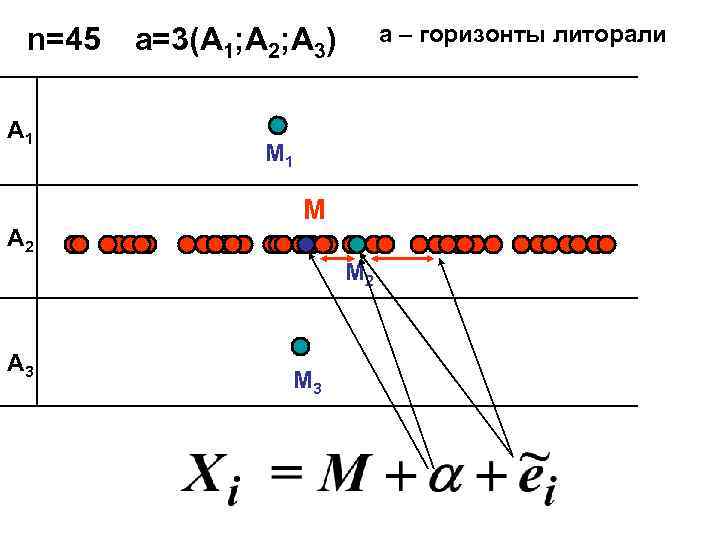
n=45 a=3(A 1; A 2; A 3) a – горизонты литорали A 1 M 1 M A 2 M 2 A 3 M 3

n=45 b=3(B 1; B 2; B 3) b – характер грунта B 1 M 1 M M 2 B 3 M 3

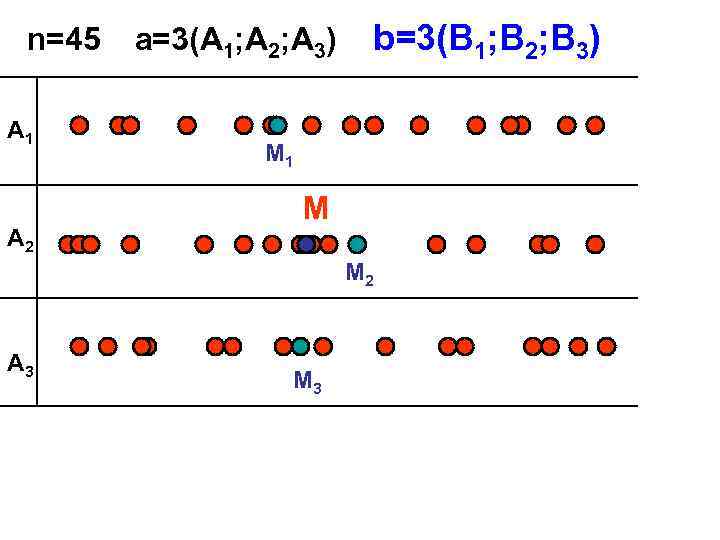
n=45 a=3(A 1; A 2; A 3) b=3(B 1; B 2; B 3) A 1 M 1 M A 2 M 2 A 3 M 3

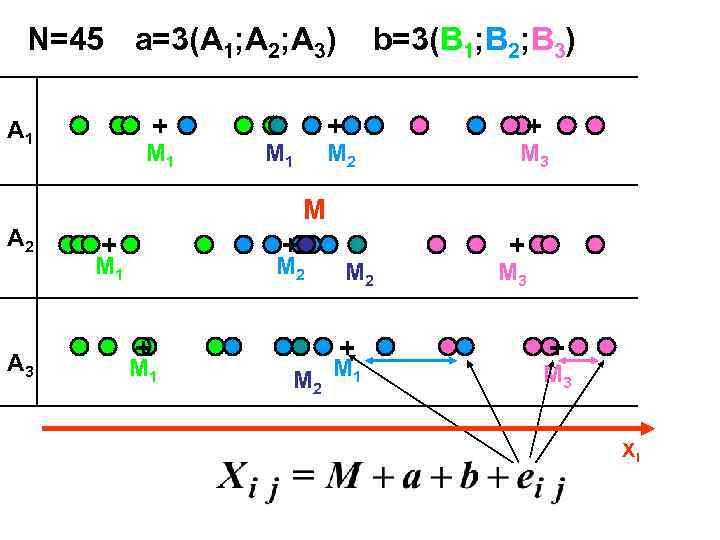
N=45 a=3(A 1; A 2; A 3) b=3(B 1; B 2; B 3) A 1 + + M 1 M 2 M 3 M A 2 + M 1 M 2 M 3 A 3 + M 1 M 2 M 1 M 3 Хi

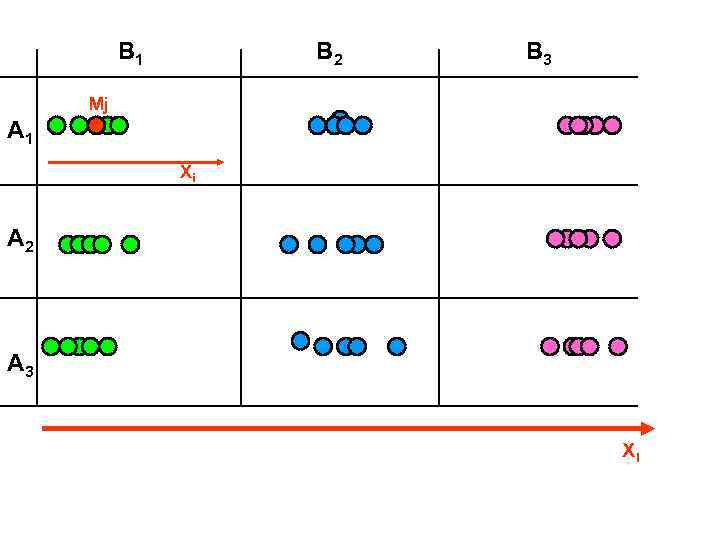
B 1 B 2 B 3 Mj A 1 Xi A 2 A 3 Хi

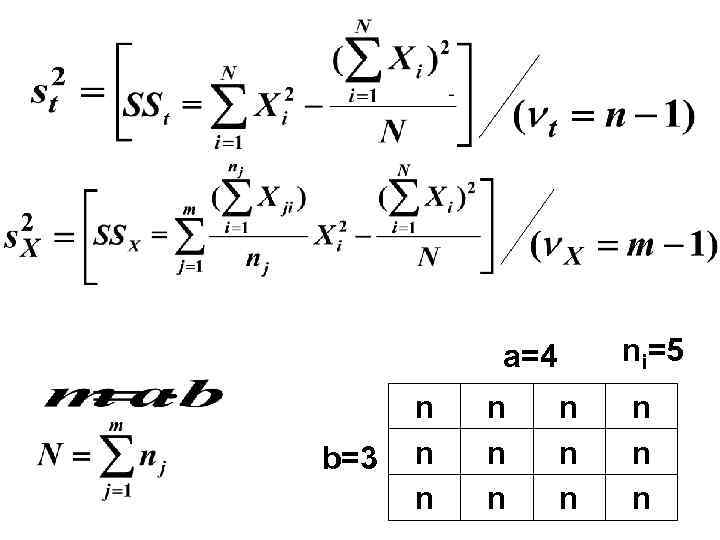
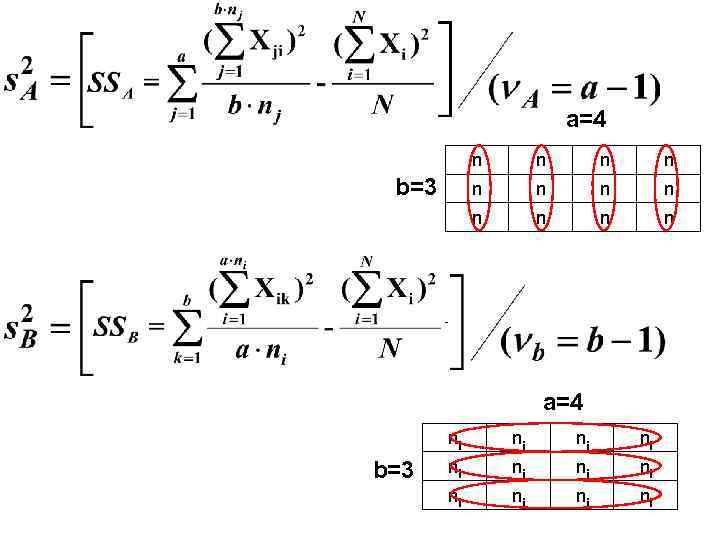
3. В условиях спланированного пробоотбора, варианты выборки образуют комплекс из аналогичных групп (ячеек) Один организованный фактор: (4 градации по фактору А: а =4) А 1 А 2 А 3 А 4 ni ni ni Два организованных фактора: (4 градации по фактору А: а =4; 2 градации по фактору В: b=2) А 1 А 2 А 3 А 4 В 1 ni ni ni В 2 ni ni ni - А и B - градации организованного воздействия на M, связанные с делением всего статистического комплекса на отдельные выборки, e - случайная ошибка.

4. Цель дисперсионного анализа - получение выводов о значимости в варьировании вариант в пределах всего комплекса: - величины е, и - организованных воздействий (А, В и т. д. ). !!! Каждый их частных выводов должен сохранять существенность независимо от других факторов.

ПРЕДПОСЫЛКИ КОРРЕКТНОСТИ ПРОЦЕДУРЫ 1. Случайность выборок (независимость вариант каждой выборки от вариант других выборок; 2. Не скоррелированность эффектов организованных воздействий на поведение вариант в пределах комплекса; 3. Нормальное распределение вариант в каждой из сравниваемых выборок; ПРИ n<30 НЕОБХОДИМО ПРЕОБРАЗОВАНИЕ ВАРИАНТ!!!. 4. Равенство варианс выборок отдельных ячеек.

ПОСТРОЕНИЕ КРИТЕРИЯ БАРТЛЕТА Если вариансы получены из независимых нормальных совокупностей, то величина имеет распределение - варианса объединенных выборок УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ. выборки принадлежат одной генеральной сово- купности, следовательно наблюдаемые различия между выборочными вариансами случайны. общий размах варьирования в дисперсионном комплексе выше, чем в какой либо отдельной ячейке (выборке). . Строим односторонний тест - критерий

ПРОВЕРЯЕТСЯ УСЛОВИЕ: m - количество выборо 5. НЕЗАВИСИМОСТЬ СРЕДНЕЙ ОТ ВАРИАНСЫ В ВЫБОРКАХ УБИРАЕТСЯ ПРИ АДЕКВАТНОМ ПРЕОБРАЗОВАНИИ ВАРИАНТ.

МОДЕЛЬ I - С ПОСТОЯННЫМИ ЭФФЕКТАМИ. 6. АДДИТИВНОСТЬ КОМПОНЕНТ ВАРИАНСЫ КОМПЛЕКСА. АДДИТИВНОСТЬ МОДЕЛИ -слагаемость компонент общей вариансы статистического комплекса, обусловленных главными эффектами воздействий. АДДИТИВНЫЙ ЭФФЕКТ - отсутствие взаимодействия.

A ONE-WAY ANOVA shouted at a TWO-WAY ANOVA: "STOP! Turn around - You are going the wrong way!" The TWO-WAY ANOVA yelled back: "Sorry! I will turn when I see an interaction!"

МОДЕЛЬ II - СО СЛУЧАЙНЫМИ ЭФФЕКТАМИ. АНАЛИЗ ОБЩЕЙ ИЗМЕНЧИВОСТИ ПРИЗНАКА ПОД ВОЗДЕЙСТВИЕМ НЕРАНЖИРОВАННОГО МНОЖЕСТВА УРОВНЕЙ ФАКТОРА. МОДЕЛЬ СО СМЕШАННЫМИ ЭФФЕКТАМИ

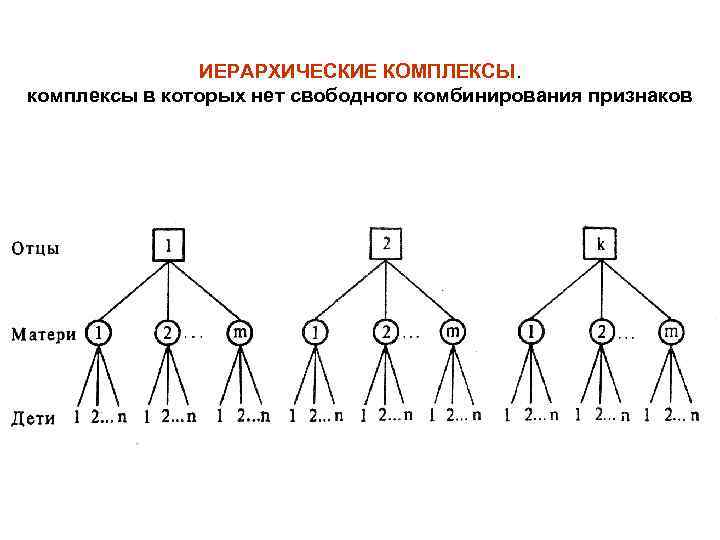
ИЕРАРХИЧЕСКИЕ КОМПЛЕКСЫ. комплексы в которых нет свободного комбинирования признаков

МОДЕЛЬ I - С ПОСТОЯННЫМИ ЭФФЕКТАМИ. ОБЩИЕ УСЛОВИЯ КОРРЕКТНОСТИ ПРОЦЕДУРЫ : - РЕАЛЬНОЕ СУЩЕСТВОВАНИЕ ВСЕХ КОМБИНАЦИЙ ФАКТОРНЫХ ВОЗДЕЙСТВИЙ; - ЗАПОЛНЕНИЕ ВСЕХ ЯЧЕЕК КОМПЛЕКСА ВАРИАНТАМИ; - ЧИСЛО ВАРИАНТ В КАЖДОЙ ЯЧЕЙКЕ НЕ НИЖЕ 2.

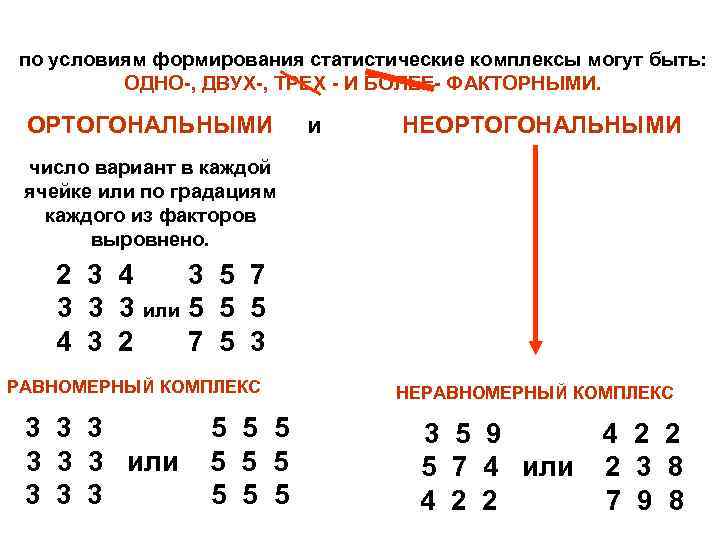
по условиям формирования статистические комплексы могут быть: ОДНО-, ДВУХ-, ТРЕХ - И БОЛЕЕ- ФАКТОРНЫМИ. ОРТОГОНАЛЬНЫМИ и НЕОРТОГОНАЛЬНЫМИ число вариант в каждой ячейке или по градациям каждого из факторов выровнено. 2 3 4 3 5 7 3 3 3 или 5 5 5 4 3 2 7 5 3 РАВНОМЕРНЫЙ КОМПЛЕКС НЕРАВНОМЕРНЫЙ КОМПЛЕКС 3 3 3 5 5 5 3 5 9 4 2 2 3 3 3 или 5 5 5 5 7 4 или 2 3 8 3 3 3 5 5 5 4 2 2 7 9 8

Пример: АНАЛИЗ РАВНОМЕРНОГО КОМПЛЕКСА т. е. различия между выборочными средними случайны средняя выборочная хотя бы ОДНОЙ ВЫБОРКИ отличается от генеральной средней. ОДНОФАКТОРНЫЙ АНАЛИЗ SSA- межгрупповая сумма квадратов (ДЕВИАТА), обусловленная различиями между выборками; SSW - внутригрупповая (остаточная, необъясненная) сумма квадратов, обусловленная варьированием признака внутри выборок.

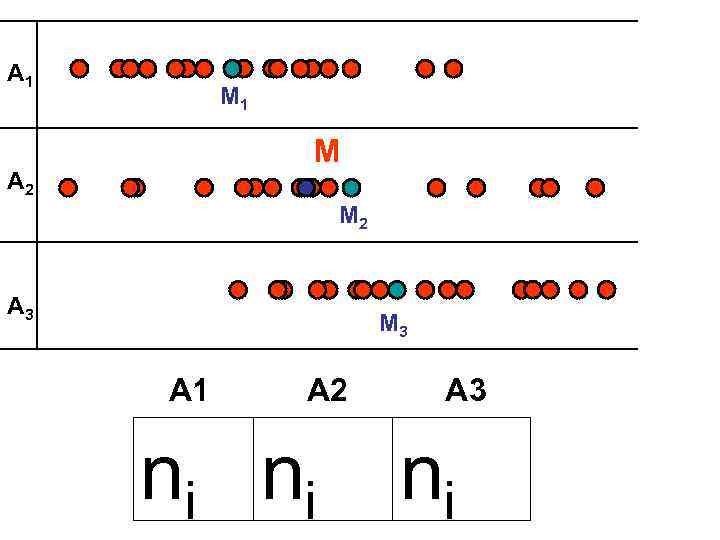
A 1 M 1 M A 2 M 2 A 3 M 3 А 1 А 2 А 3 ni ni ni

ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА:

ДВУХФАКТОРНЫЙ АНАЛИЗ. АДДИТИВНАЯ МОДЕЛЬ: МОДЕЛЬ СО ВЗАИМОДЕЙСТВИЕМ ФАКТОРОВ: SSA- межгрупповая (факториальная) сумма квадратов, обусловленная различиями между выборками градаций фактора А; SSB - межгрупповая (факториальная) сумма квадратов, обусловленная различиями между выборками градаций фактора B; SSАB - сумма квадратов, обусловленная эффектами совместного воздействия факторов; SSW - внутригрупповая (остаточная, необъясненная) сумма квадратов, обусловлена варьированием признака внутри отдельных выборок.

a=4 ni=5 n n b=3 n n

a=4 n n b=3 n n a=4 ni ni b=3 ni ni

Эффект неаддитивности выразится в неравенстве: Отсюда: .

КРИТЕРИЙ СТРОИТСЯ КАК ОДНОСТОРОННИЙ ТЕСТ ПО КАЖДОМУ ИЗ ПРОВЕРЯЕМЫХ ВОЗДЕЙСТВИЙ: .

ОПРЕДЕЛЕНИЕ СИЛЫ ВЛИЯНИЯ ФАКТОРА ПО ПЛОХИНСКОМУ СТАТИСТИКА ПОКАЗАТЕЛЯ ПОДЧИНЯЕТСЯ СИЛЫ ВЛИЯНИЯ ФАКТОРА F-РАСПРЕДЕЛЕНИЮ КРИТЕРИЙ ДОСТОВЕРНОСТИ - ОТНОШЕНИЕ СИЛЫ ВЛИЯНИЯ К ОШИБКЕ: влияние фактора соизмеримо с ошибкой оценки и потому вывод о достоверности силы влияния ненадежен. влияние фактора достоверно. ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА:

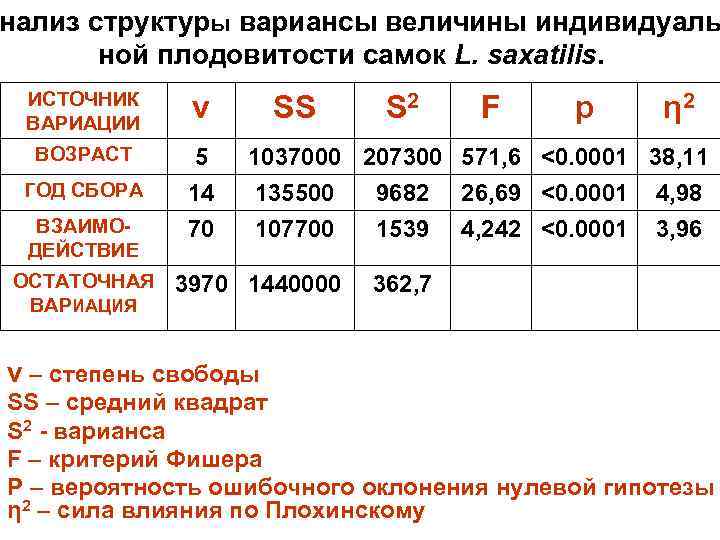
нализ структуры вариансы величины индивидуаль ной плодовитости самок L. saxatilis. ИСТОЧНИК ВАРИАЦИИ ν SS S 2 F р η 2 ВОЗРАСТ 5 1037000 207300 571, 6 <0. 0001 38, 11 ГОД СБОРА 14 135500 9682 26, 69 <0. 0001 4, 98 ВЗАИМО- 70 107700 1539 4, 242 <0. 0001 3, 96 ДЕЙСТВИЕ ОСТАТОЧНАЯ 3970 1440000 362, 7 ВАРИАЦИЯ v – степень свободы SS – средний квадрат S 2 - варианса F – критерий Фишера Р – вероятность ошибочного оклонения нулевой гипотезы η 2 – сила влияния по Плохинскому

Влияние нарушений процедуры анализа на выводы. I - нарушение предположение о случайности вариант в выборках радикально влияет на выводы о средних, полученных с использованием t-статистики и F-критерия. II - нарушение нормальности распределения вариант оказывает слабое действие на выводы о средних, СНИЖАЕТСЯ МОЩНОСТЬ КРИТЕРИЯ ФИШЕРА. ! НО СИЛЬНО ВЛИЯЕТ НА ВЫВОДЫ О ВАРИАНСАХ. Критерий Бартлета при Еs <0 несколько затушевывает отличие варианс, а при Еs >0 - может ошибочно указать на неоднородность варианс в комплексе.

III - нарушение условия равенства варианс мало влияет на выводы о средних, если ОБЪЕМЫ ВЫБОРОК РАВНЫ. IV - аппарат дисперсионного анализа без преобразования вариант можно с успехом применять если их распределение в комплексе куполообразно и не резко асимметрично, а групповые вариансы отличаются друг от друга не более, чем в 2. 5 раза. Большие различия варианс допустимы только в ОРТОГОНАЛЬНЫХ КОМПЛЕКСАХ.

РАБОТА С НЕОРТОГОНАЛЬНЫМИ КОМПЛЕКСАМИ 1. Система расчета по Поморскому. Замена неравномерного комплекса равномерным, с усреднением (выравниваем частот) по градациям. 2. Система расчета по Немчинову. Замена неравномерного комплекса равномерным, с усреднением (выравниваем частот) по по градациям, но другим образом (через среднюю гармоническую). 3. Система расчета по Плохинскому. Определение поправок к факториальным девиатам. Н. А. Плохинский. Дисперсионный анализ. Новосибирск, 1960

Модель II со случайными эффектами

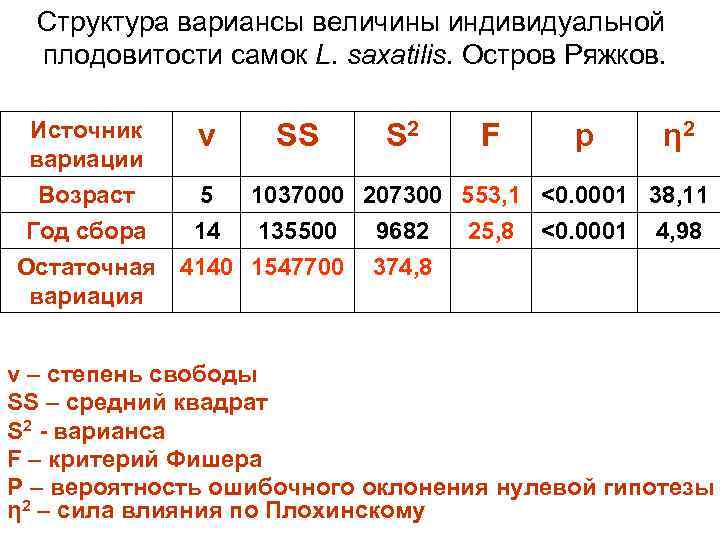
Структура вариансы величины индивидуальной плодовитости самок L. saxatilis. Остров Ряжков. Источник ν SS S 2 F р η 2 вариации Возраст 5 1037000 207300 553, 1 <0. 0001 38, 11 Год сбора 14 135500 9682 25, 8 <0. 0001 4, 98 Остаточная 4140 1547700 374, 8 вариация v – степень свободы SS – средний квадрат S 2 - варианса F – критерий Фишера Р – вероятность ошибочного оклонения нулевой гипотезы η 2 – сила влияния по Плохинскому

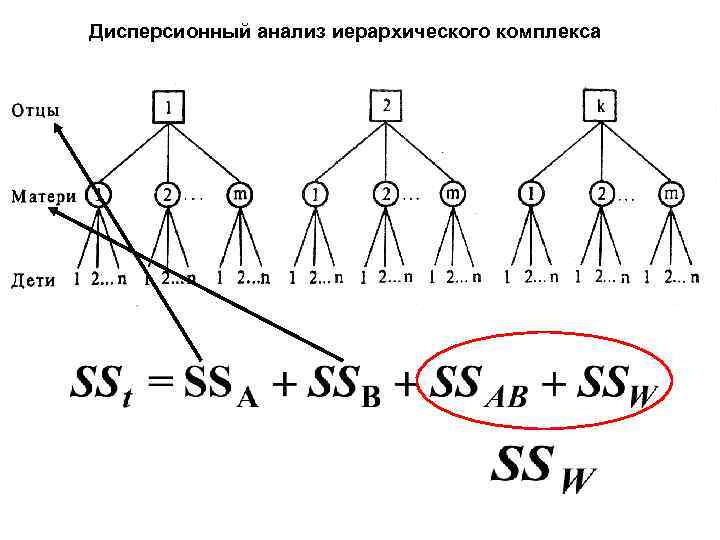
Дисперсионный анализ иерархического комплекса

Непараметрические критерии Критерий Краскела-Уоллиса: ранговый - проверка однородности при одном факторе определение неоднородности нескольких выборок при одном действующем факторе Критерий Джонкхиера для альтернатив с упорядочением вариант критерия Манна-Уитни для случаев нескольких выборок Критерий Фридмана : ранговый - проверка однородности комплекса при двух факторах то же, что и статистика Краскела-Уоллеса, но при двух действующих факторах. Критерий Пейджа для альтернатив с упорядочением Вариант дисперсионного анализа рангов

МЕТОДЫ МНОЖЕСТВЕННОГО СРАВНЕНИЯ КРИТЕРИЙ БОНФЕРОНИ Критерий Стьюдента для множественного сравнений. Метод работает, если число сравнений невелико, обычно не больше 8. Если больше, то КРИТЕРИЙ НЬЮМАНА-КЕУЛСА КРИТЕРИЙ ТЬЮКИ

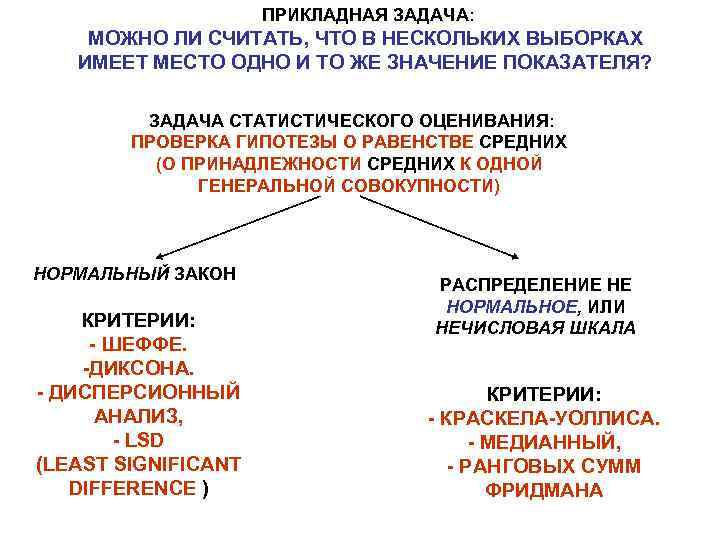
ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЯ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ (О ПРИНАДЛЕЖНОСТИ СРЕДНИХ К ОДНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ) НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ КРИТЕРИИ: НЕЧИСЛОВАЯ ШКАЛА - ШЕФФЕ. -ДИКСОНА. - ДИСПЕРСИОННЫЙ КРИТЕРИИ: АНАЛИЗ, - КРАСКЕЛА-УОЛЛИСА. - LSD - МЕДИАННЫЙ, (LEAST SIGNIFICANT - РАНГОВЫХ СУММ DIFFERENCE ) ФРИДМАНА

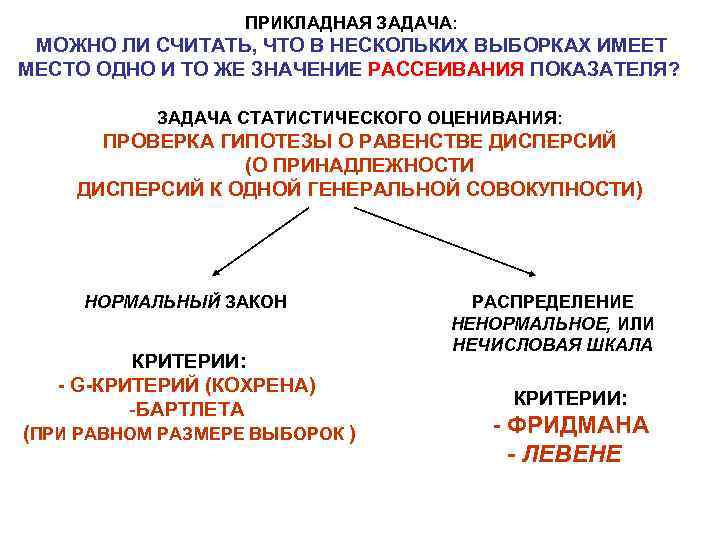
ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ РАССЕИВАНИЯ ПОКАЗАТЕЛЯ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ (О ПРИНАДЛЕЖНОСТИ ДИСПЕРСИЙ К ОДНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ) НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЕ НЕНОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - G-КРИТЕРИЙ (КОХРЕНА) КРИТЕРИИ: -БАРТЛЕТА (ПРИ РАВНОМ РАЗМЕРЕ ВЫБОРОК ) - ФРИДМАНА - ЛЕВЕНЕ

Градиентные построения по итогам дисперсионного анализа t Поведение средних величин годового прироста L. saxatilis на станции у о. Ряжков при изменении возраста и места сбора (А – верхний, В – средний и С – нижний горизонты литорали) моллюсков. По оси ординат – годовой прирост, мм; по оси абсцисс – возраст моллюсков (годы)