ОБС_05_2015.ppt
- Количество слайдов: 54

ОБС 5 ОСНОВЫ БИОСТАТИСТИКИ http: //www. hydrobiology. spb. ru БИБЛИОТЕКА Biostat-1 Biostat-2 Biostat-3 Biostat-4 Biostat-5 Фото: Risto Vainola
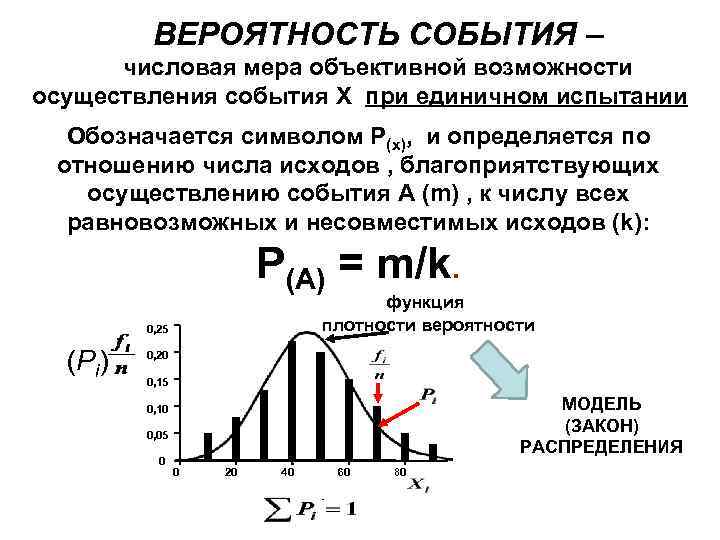
ВЕРОЯТНОСТЬ СОБЫТИЯ – числовая мера объективной возможности осуществления события X при единичном испытании Обозначается символом Р(x), и определяется по отношению числа исходов , благоприятствующих осуществлению события A (m) , к числу всех равновозможных и несовместимых исходов (k): Р(A) = m/k. функция плотности вероятности 0, 25 (Рi) 0, 20 0, 15 МОДЕЛЬ (ЗАКОН) РАСПРЕДЕЛЕНИЯ 0, 10 0, 05 0 0 20 40 60 X i 80 i

Модели распределений дискретных случайных величин. БИНОМИАЛЬНЫЙ ЗАКОН Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при k независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие А’ с вероятностью Р(A’) = 1 - р = q. Вероятности появления событий m в k независимых испытаний соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний: Jakob Bernoulli 1654 -1705 Sir Isaac Newton (1642 - 1727) http: //igriki. narod. ru/binom_raspr 1. htm

БИНОМИАЛЬНЫЙ ЗАКОН Свойства биномиального распределения ∑Pk(m) = (p+q)k = 1 Формула бинома Ньютона (р+q)k - Частота m появления ожидаемого события А в k независимых испытаний определяется его вероятностью р , постоянной в каждом испытании. - Характер биномиальной кривой определяется двумя величинами: числом испытаний (k) и вероятностью р ожидаемого результата. p=q ПРИ БИНОМИАЛЬНАЯ КРИВАЯ СТРОГО СИММЕТРИЧНА ОТНОСИТЕЛЬНО МАКСИМАЛЬНОЙ ОРДИНАТЫ, ЯВЛЯЮЩЕЙСЯ ЦЕНТРОМ РАСПРЕДЕЛЕНИЯ. ПРИ р<>q БИНОМИАЛЬНАЯ КРИВАЯ АСИММЕТРИЧНА.

БИНОМИАЛЬНЫЙ ЗАКОН ФОРМУЛА БЕРНУЛИ - случайное событие А - k независимых испытаний - в каждом испытании вероятность p (А) постоянна. - два исхода: появление события А или события А*. - Вероятность события А* равна q. р+q=1 - если в k испытаниях событие А появится m раз, то событие А* появится k-m раз. - вероятность появление события А в k испытаниях m раз (pk(m)) выражается произведением рmqk-m, умноженным на биномиальный коэффициент , P(A)=Сkm рmqk-m
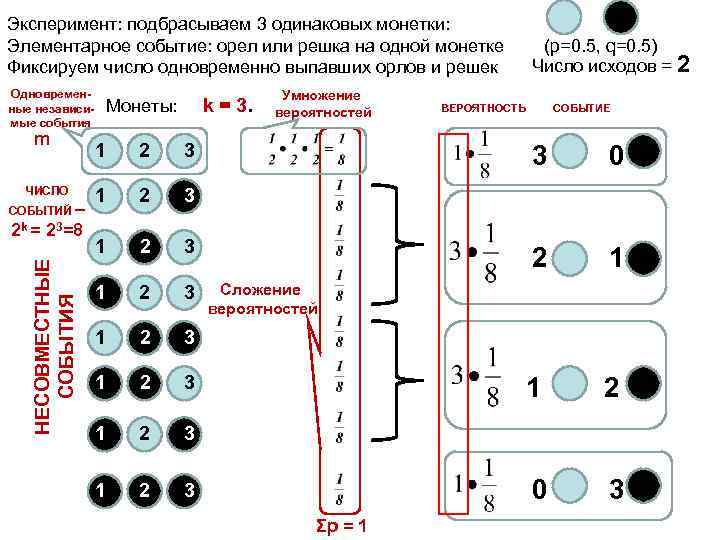
Эксперимент: подбрасываем 3 одинаковых монетки: Элементарное событие: орел или решка на одной монетке Фиксируем число одновременно выпавших орлов и решек Одновременные независимые события m ЧИСЛО НЕСОВМЕСТНЫЕ СОБЫТИЯ СОБЫТИЙ – 2 k = 23=8 Монеты: Умножение k = 3. вероятностей 1 2 3 (р=0. 5, q=0. 5) Число исходов = 2 ВЕРОЯТНОСТЬ СОБЫТИЕ 3 0 1 2 3 2 1 Сложение вероятностей 1 2 3 1 2 1 2 3 0 3 1 2 3 Σp = 1

Число независимых испытаний (k) Треугольник Паскаля Б. Паскаль «Трактат об арифметическом треугольнике» (1655).

БИНОМИАЛЬНЫЙ ЗАКОН Пример 2 : Какова вероятность появления 0, 1, 2, 4 или 5 особей мужского пола в числе 5 новорожденных? Событие А (рождение мальчика) – m меняется от 0 до 5 случаев k = 5 Событие А* (рождение девочки) m меняется от 0 до 5 случаев В каждом наблюдении p(А) = q(А*) = 0, 5. m=0 Р(0) = 0, 03125; Р(1) = 0, 15625; m=1 Р(2) = 0, 3125; Р(3) = 0, 3125; , m=2 P(A)=С 0, 15625 Р(4) = km рmqk-m Р(5) = 0, 03125.

Число независимых испытаний (k) Треугольник Паскаля Б. Паскаль «Трактат об арифметическом треугольнике» (1655).
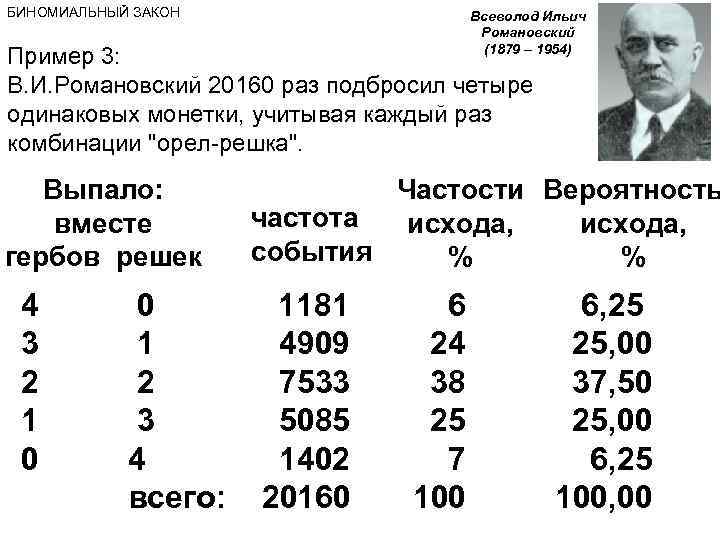
БИНОМИАЛЬНЫЙ ЗАКОН Всеволод Ильич Романовский (1879 – 1954) Пример 3: В. И. Романовский 20160 раз подбросил четыре одинаковых монетки, учитывая каждый раз комбинации "орел-решка". Выпало: вместе гербов решек Частости Вероятность частота исхода, события % % 4 0 1181 6 6, 25 3 1 4909 24 25, 00 2 2 7533 38 37, 50 1 3 5085 25, 00 0 4 1402 7 6, 25 всего: 20160 100, 00
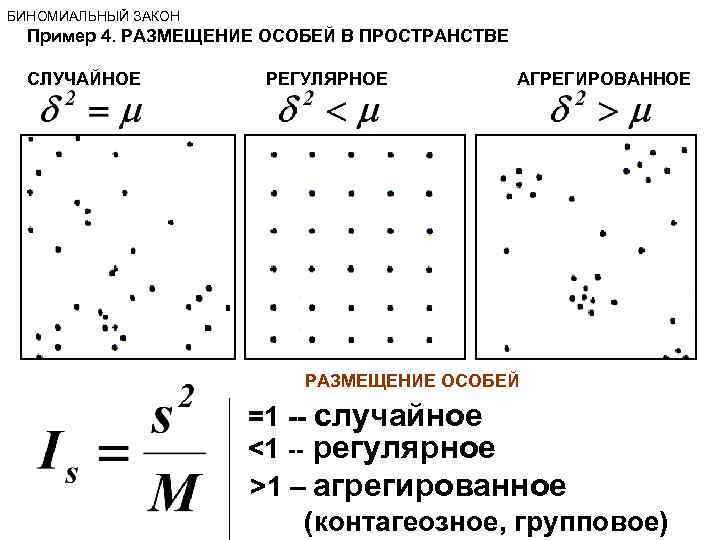
БИНОМИАЛЬНЫЙ ЗАКОН Пример 4. РАЗМЕЩЕНИЕ ОСОБЕЙ В ПРОСТРАНСТВЕ СЛУЧАЙНОЕ РЕГУЛЯРНОЕ АГРЕГИРОВАННОЕ РАЗМЕЩЕНИЕ ОСОБЕЙ =1 -- случайное <1 -- регулярное >1 – агрегированное (контагеозное, групповое)
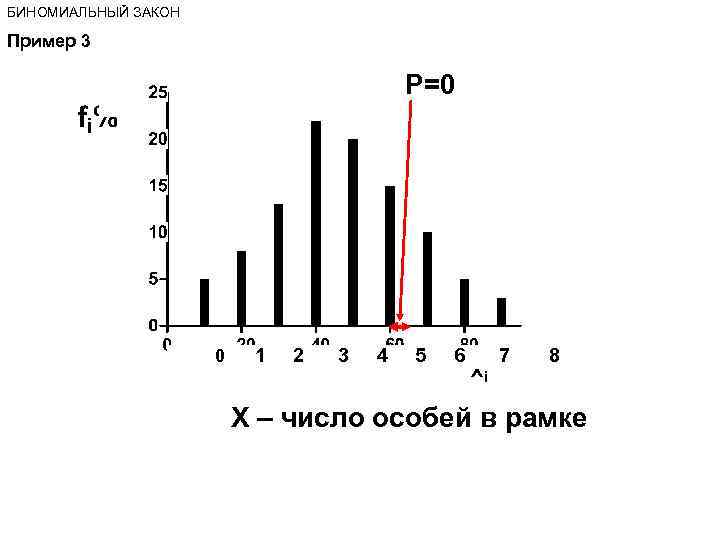
БИНОМИАЛЬНЫЙ ЗАКОН Пример 3 P=0 0 1 2 3 4 5 6 7 8 Х – число особей в рамке

БИНОМИАЛЬНЫЙ ЗАКОН РЕГУЛЯРНОЕ РАЗМЕЩЕНИЕ ОСОБЕЙ модель ПОЛОЖИТЕЛЬНОЕ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (q+p)k p - вероятность попадания одной особи в выборочную площадку; q - вероятность того, что в выборочную площадку не попадет ни одна особь; k - максимально возможное число особей в выборочной площадке. . k ~ M 2/(M - s 2); p ~ M/k; M ~ kp; s 2 ~ kpq; p+q = 1;

СЛУЧАЙНОЕ РАЗМЕЩЕНИЕ ОСОБЕЙ В МЕСТООБИТАНИИ модель РАСПРЕДЕЛЕНИЕ ПУАССОНА Теорема. Если вероятность р наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний k достаточно велико, произведение kp = λ, то вероятность Рk(m) того, что в k независимых испытаниях события А наступит m раз, приближенно равна Siméon-Denis Poisson (1781 - 1840) Закон Пуассона – это закон распределения редких событий. Классический пример – попадание бомб в разные кварталы Лондона. Примеры из биологии: - нарушение хромосомного аппарата на каждую тысячу митозов; - встречаемость семян сорняка в большой серии навесок семян культурного растения; - число повторных попаданий животных в ловушки; - распределение редких форм в местообитаниях; - отловы животных в отдельные промежутки времени при длительных наблюдениях.

СЛУЧАЙНОЕ РАЗМЕЩЕНИЕ ОСОБЕЙ в местообитаниях Вероятность того, что в рамке окажется Х особей вычисляется по формуле: Р(X)= e- ( Х/X!) m=s 2=M p - вероятность попадания одной особи в выборочную площадку; q - вероятность того, что в выборочную площадку не попадет ни одна особь; Распределение Пуассона это частный (предельный) случай биномиального распределения при р -->0 и k-->. Тогда: р =М/k и q-->1 по мере того как s 2 -->M. М, или s 2 – соответствует наивероятнейшей частоте ожидаемого события (мода).

Распределение Пуассона Условия коректности описания эмпирического распределения моделью Пуассона 1. Вероятность оккупирования одной особью выбранной площадки мала и постоянна. 2. M < Xmax 3. Присутствие особи в выборочной площадке не должно влиять на вероятность попадания особи в соседнюю площадку. 4. n<<<N 5. При (s 2, M) >10 распределение Пуассона асимптотически приближается к нормальному

БИНОМИАЛЬНЫЙ ЗАКОН Агрегированное размещения особей модель ОТРИЦАТЕЛЬНОЕ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (q-p)-k p - вероятность попадания одной особи в выборочную площадку; q - вероятность того, что в выборочную площадку не попадет ни одна особь; к - степень агрегации k ~ (M 2 -S 2/n)/(s 2 -M); p ~ 1/(1 -M/k); 2 ~ kpq M ~ kq/p; s

СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ

A Physicist, a Biologist, and a Statistician see two people enter a house, and then after some time, they see three people leave the house. The Physicist concludes, "My initial observation must have been incorrect. " The Biologist concludes, "Clearly, the two reproduced. . . " The Statistician concludes, "Well, if one more person enters the house, then there will be no one in the house!"

Условия корректности процедур в биометрии 1. - независимость вариант друг от друга (случайность наблюдений); 2. - “нормальность” или возможность нормализации вариационных рядов; 3. - независимостью выборочных показателей распределения друг от друга; 4. - аддитивностью компонентов вариансы, т. е. сложимости эффектов основных воздействий на изучаемый признак в статистическом комплексе; 5. - равенство варианс выборок.

Pierre-Simon Laplace (1749 -1827) Siméon Denis Poisson (1781 – 1840) Чебышёв Пафну тий Льво вич (1821 – 1894) Марков Андрей Андреевич (1856 – 1922) Ляпуно в Алекса ндр Миха йлович (1857 – 1918) ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ: 1 -я группа теорем составляет "закон больших чисел". Закон больших чисел формулирует условия, при которых совокупное действие большого числа случайных факторов приводит к результату почти не зависящему от случая (т. е. практически постоянный результат) 2 -я группа теорем связана с выяснением вопроса о распределении сумм большого числа случайных величин. В этих теоремах выясняется, какие законы распределения может иметь сумма случайных величин, если число слагаемых неограниченно увеличивается.

МЕСТО НОРМАЛЬНОГО ЗАКОНА В БИОСТАТИСТИКЕ ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА (Лаплас, 1813 г. ) Интегральная предельная теорема Муавра-Лапласа является частным случаем общей и универсальной центральной предельной теоремы. Pierre-Simon Laplace (1749 — 1827) Она утверждает, что число успехов при многократном повторении одного и того же случайного эксперимента с двумя возможными исходами приблизительно имеет нормальное распределение. Обобщение ЦПТ на случай, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, имеющих разные распределения, дисперсии которых малы по сравнению с дисперсией суммы. Закон распределения такой случайной величины оказывается практически нормальным законом. Ляпуно в Алекса ндр Миха йлович (1857 – 1918)

МЕСТО НОРМАЛЬНОГО ЗАКОНА В БИОСТАТИСТИКЕ Ляпуно в Алекса ндр Миха йлович (1857 – 1918) Один из основных постулатов ЦПТ : …. закон распределения суммы большого числа нормированных случайных слагаемых (=распределений) практически вне зависимости от типа распределения самих слагаемых стремится по мере роста числа слагаемых к нормальному (гауссовскому) распределению Именно теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования
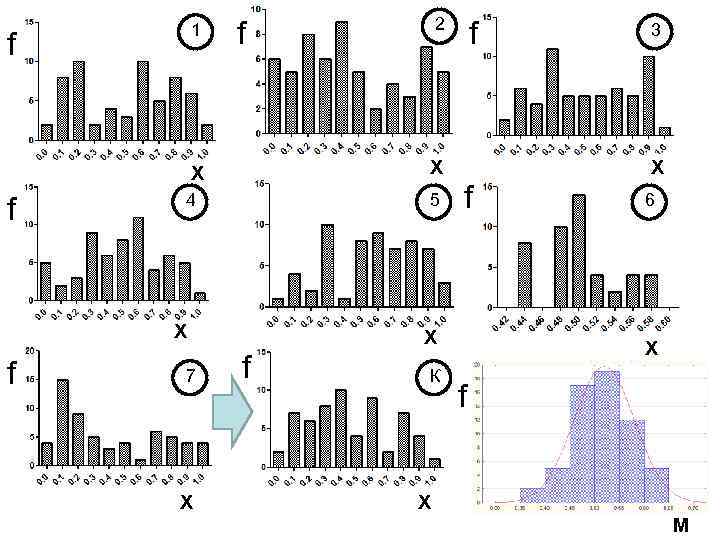
1 f 4 5 X f 7 X f X X f 2 f X f К 3 6 X f X M

Итак. . . … средние больших случайных выборок, полученных из одной генеральной совокупности, будут распределены нормально, и независимо от типа распределения вариант в каждой выборке. . . очень часто вероятность Pi “Каждый уверен в любого значения Xi справедливости непрерывно меняющейся нормального закона: случайной величины X, экспериментаторы – находящегося в интервале от потому, что они думают, X до Х+d. Х, выражается что это математическая теорема; математики Формулой: потому, что они думают, что это Jules Henri экспериментальный Gabriel Lipman Poincaré факт” 1854 - 1912 ? 1845 - 1921

ОДНО ИЗ ГЛАВНЫХ УСЛОВИЙ КОРРЕКТНОСТИ ПРОЦЕДУР В МАТСТАТИСТИКЕ . . “НОРМАЛЬНОСТЬ” ИЛИ ВОЗМОЖНОСТЬ НОРМАЛИЗАЦИИ ИСХОДНЫХ ВАРИАЦИОННЫХ РЯДОВ. . . МОЖНО ВЫПОЛНИТЬ ВСПОМНИВ, ЧТО. . А) существуют прямые и косвенные оценки, позволяющие обойти сложные процедуры, предписанные для включения «ненормальных» данных в статистический анализ. Б) даже в случае доказанного отклонения исследуемых экспериментальных распределений от нормального закона есть по крайней мере два пути его целесообразной эксплуатации: 1. - использование нормального закона в качестве первого правдоподобного приближения. 2. - подбор такого преобразования исследуемой случайной величины, которое превращает исходный “ненормальный” ряд распределения в «нормальный» . .

«Есть просто ложь, есть большая ложь и есть статистика» «Есть просто ложь, наглая ложь и статистика» . . . имеется три вида лжи: . . . ложь вынужденная, которая извинительна, во-вторых, ложь низкая – ей нет никакого извинения, и в третьих, - статистика. . . ? Бенджамин Дизраэли Benjamin Disraeli, lord Beaconsfield, 1804— 1881 Марк Твен Samuel Langhorne Clemens (1835 -1910)

НОРМАЛЬНЫЙ ЗАКОН И БИНОМИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ Регулярное размещение особей (модель - положительный бином) примерно соответствует нормальному закону, если выборка велика (n >30) и варианса (S 2 = Kpq) не меньше 3. Нормальная аппроксимация такого вариационного ряда возможна: При k от 10 до 30, а p от 0. 4 до 0. 6 , При k > 30, p может принимать значения от 0. 1 до 0. 9.
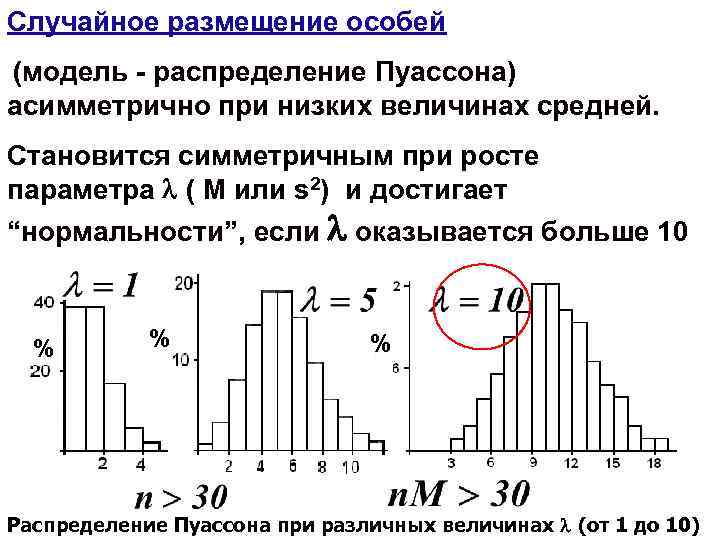
Случайное размещение особей (модель - распределение Пуассона) асимметрично при низких величинах средней. Становится симметричным при росте параметра ( М или s 2) и достигает “нормальности”, если оказывается больше 10 % % % Распределение Пуассона при различных величинах (от 1 до 10)
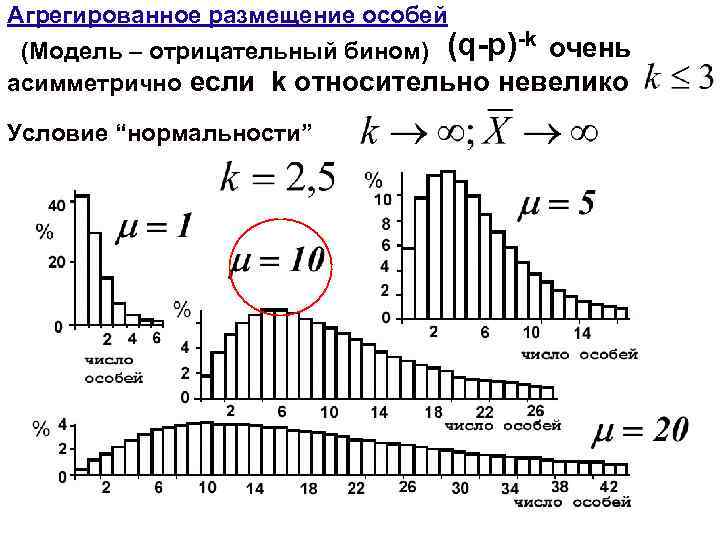
Агрегированное размещение особей -k (Модель – отрицательный бином) (q-p) очень асимметрично если k относительно невелико Условие “нормальности”
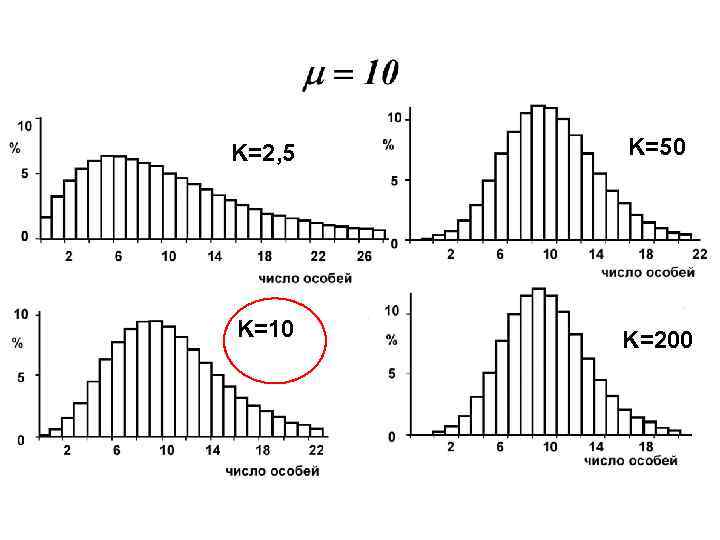
K=2, 5 K=50 K=10 K=200
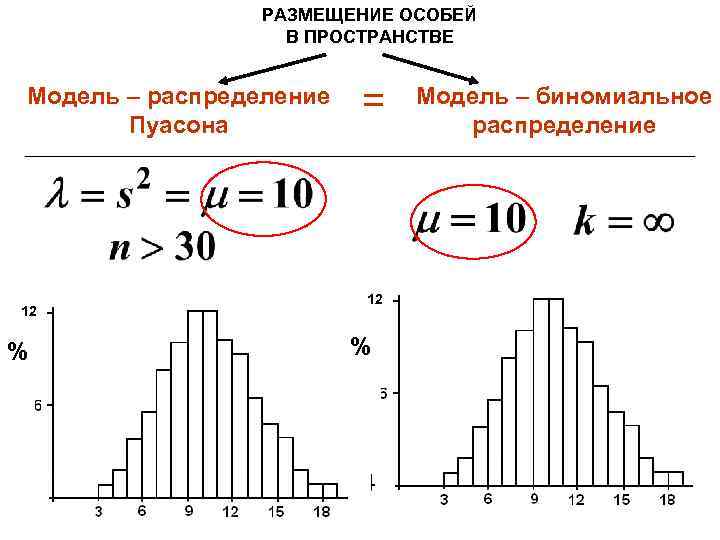
РАЗМЕЩЕНИЕ ОСОБЕЙ В ПРОСТРАНСТВЕ Модель – распределение Пуасона 12 % = 12 % Модель – биномиальное распределение

практическое правило - в популяционных исследованиях следует выбирать такой режим пробоотбора, что бы в учетной площадке в среднем оказывалось не менее 10 особей.
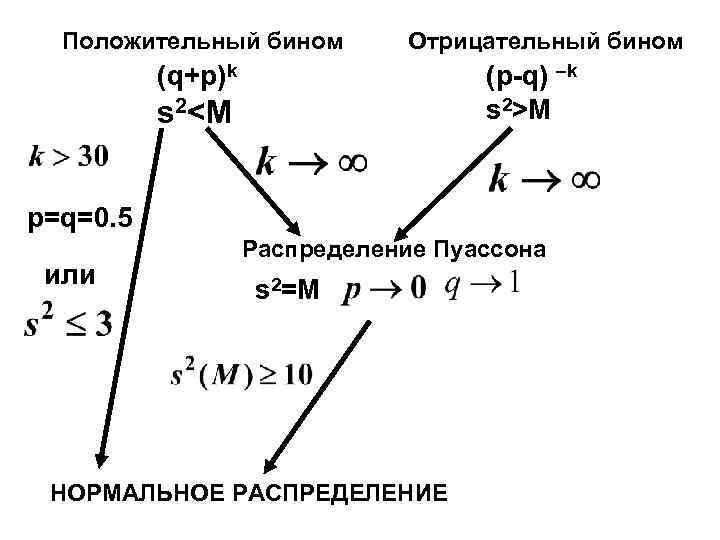
Положительный бином Отрицательный бином (q+p)k (p-q) –k s 2>M s 2<M p=q=0. 5 или Распределение Пуассона s 2=M НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
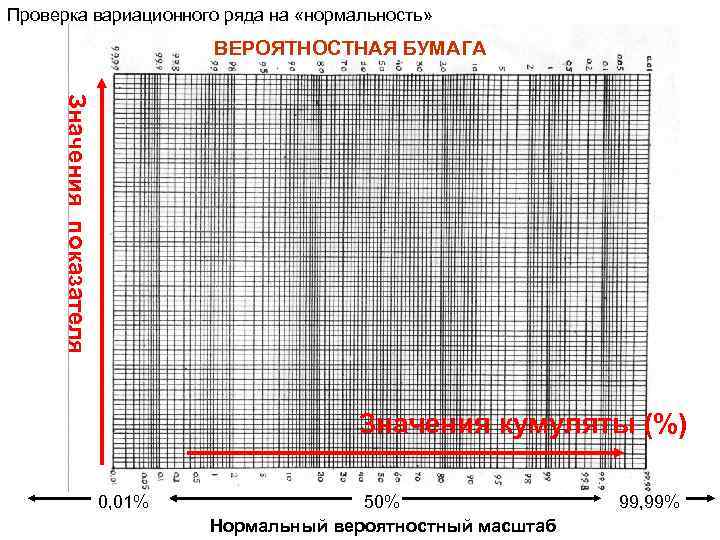
Проверка вариационного ряда на «нормальность» ВЕРОЯТНОСТНАЯ БУМАГА Значения показателя Значения кумуляты (%) 0, 01% 50% Нормальный вероятностный масштаб 99, 99%
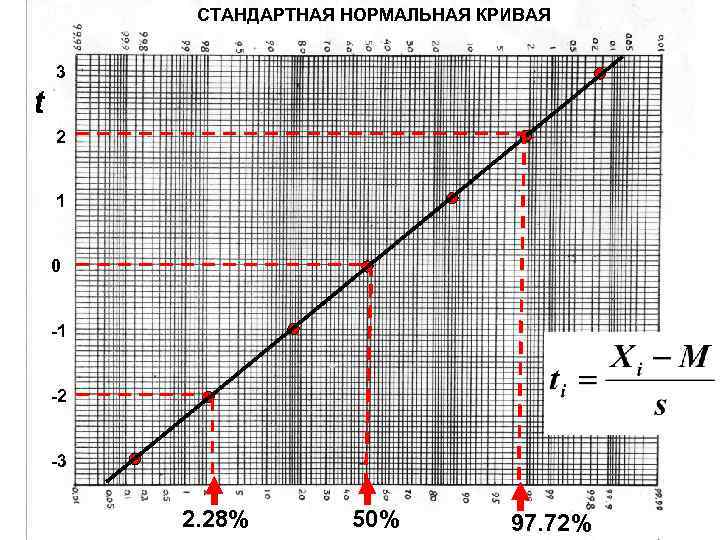
СТАНДАРТНАЯ НОРМАЛЬНАЯ КРИВАЯ 3 t 2 1 0 -1 -2 -3 2. 28% 50% 97. 72%
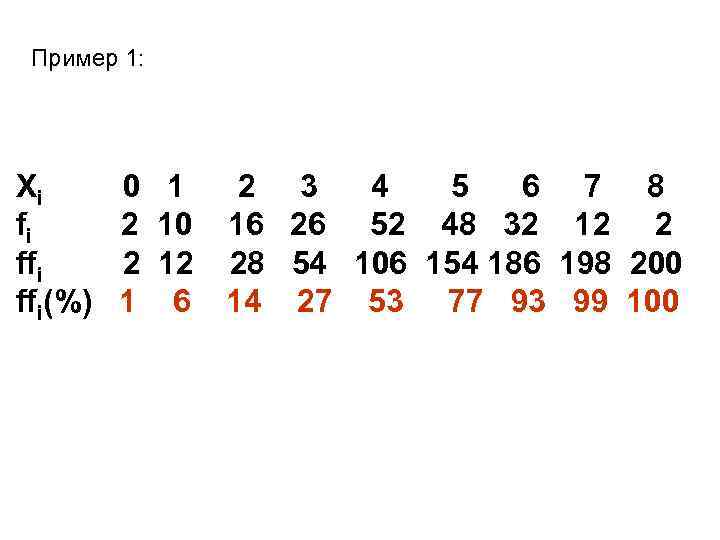
Пример 1: Хi 0 1 2 3 4 5 6 7 8 fi 2 10 16 26 52 48 32 12 2 ffi 2 12 28 54 106 154 186 198 200 ffi(%) 1 6 14 27 53 77 93 99 100
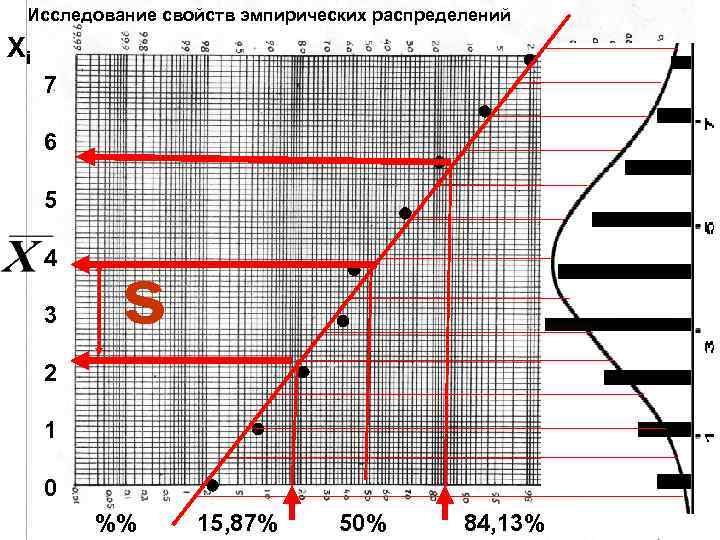
Исследование свойств эмпирических распределений Xi 7 6 5 4 3 s 2 1 0 %% 15, 87% 50% 84, 13%
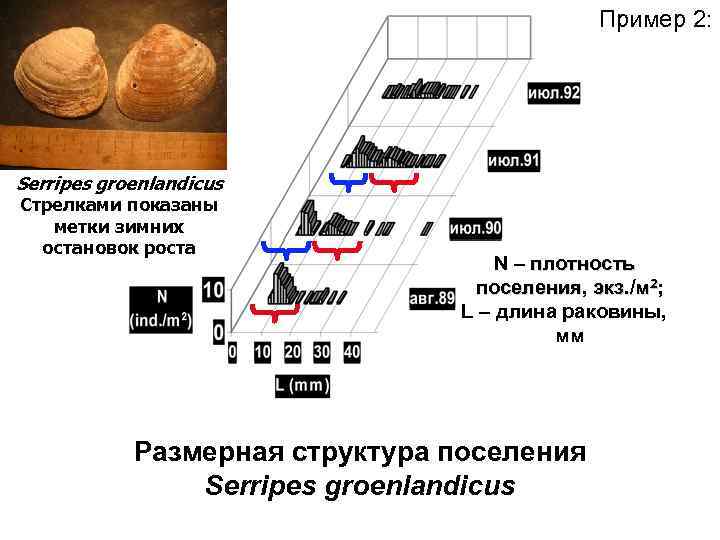
Пример 2: Serripes groenlandicus Стрелками показаны метки зимних остановок роста N – плотность поселения, экз. /м 2; L – длина раковины, мм Размерная структура поселения Serripes groenlandicus
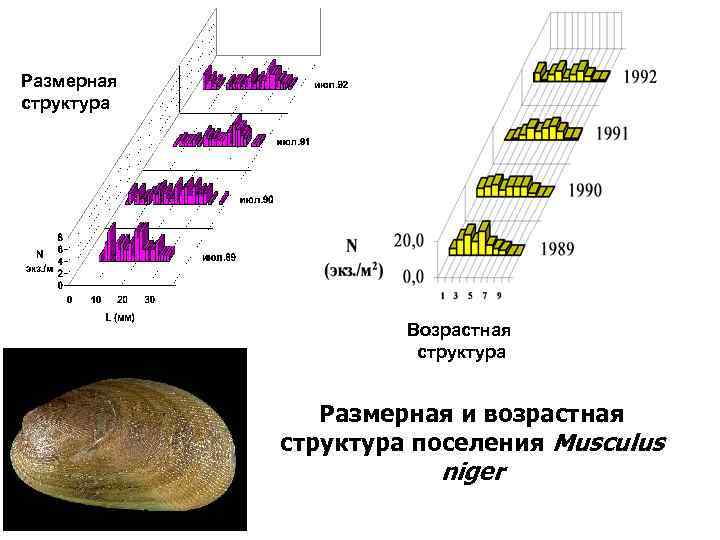
Размерная структура Возрастная структура Размерная и возрастная структура поселения Musculus niger
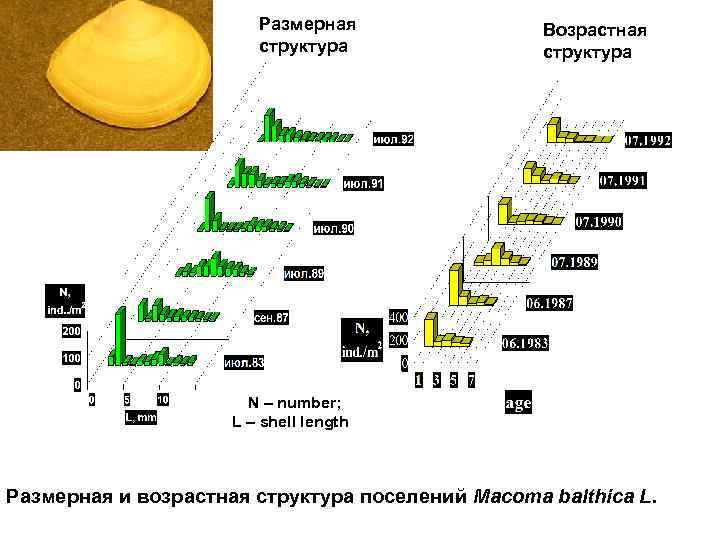
Размерная структура Возрастная структура N – number; L – shell length Размерная и возрастная структура поселений Macoma balthica L.
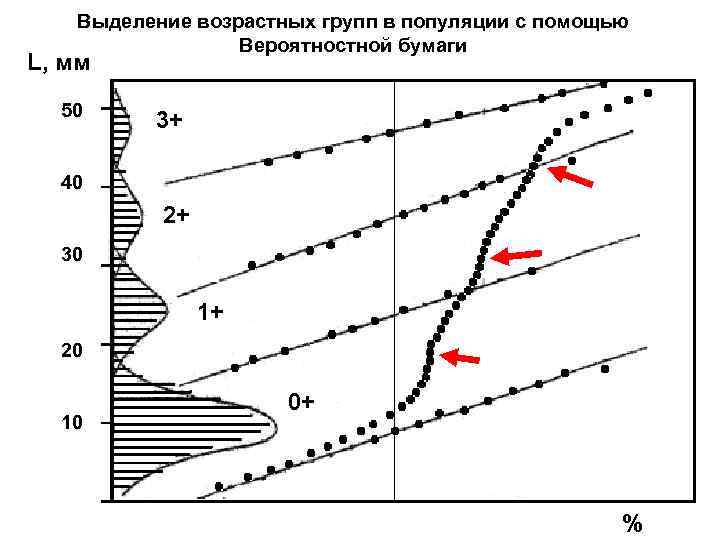
Выделение возрастных групп в популяции с помощью Вероятностной бумаги L, мм 50 3+ 40 2+ 30 1+ 20 10 0+ %

1986
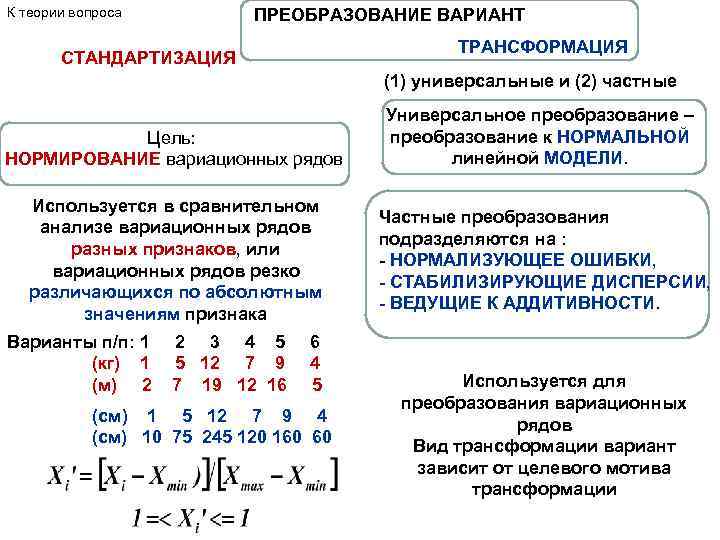
К теории вопроса ПРЕОБРАЗОВАНИЕ ВАРИАНТ СТАНДАРТИЗАЦИЯ ТРАНСФОРМАЦИЯ (1) универсальные и (2) частные Цель: НОРМИРОВАНИЕ вариационных рядов Используется в сравнительном анализе вариационных рядов разных признаков, или вариационных рядов резко различающихся по абсолютным значениям признака Варианты п/п: 1 2 3 4 5 6 (кг) 1 5 12 7 9 4 (м) 2 7 19 12 16 5 (см) 1 5 12 7 9 4 (см) 10 75 245 120 160 60 Универсальное преобразование – преобразование к НОРМАЛЬНОЙ линейной МОДЕЛИ. Частные преобразования подразделяются на : - НОРМАЛИЗУЮЩЕЕ ОШИБКИ, - СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИИ, - ВЕДУЩИЕ К АДДИТИВНОСТИ. Используется для преобразования вариационных рядов Вид трансформации вариант зависит от целевого мотива трансформации
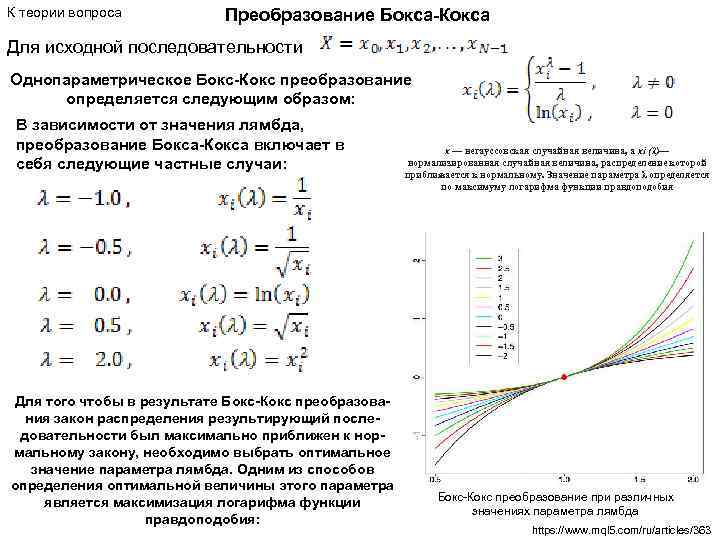
К теории вопроса Преобразование Бокса-Кокса Для исходной последовательности Однопараметрическое Бокс-Кокс преобразование определяется следующим образом: В зависимости от значения лямбда, преобразование Бокса-Кокса включает в себя следующие частные случаи: Для того чтобы в результате Бокс-Кокс преобразования закон распределения результирующий последовательности был максимально приближен к нормальному закону, необходимо выбрать оптимальное значение параметра лямбда. Одним из способов определения оптимальной величины этого параметра является максимизация логарифма функции правдоподобия: x — негауссовская случайная величина, а xi (λ)— нормализированная случайная величина, распределение которой приближается к нормальному. Значение параметра λ определяется по максимуму логарифма функции правдоподобия Бокс-Кокс преобразование при различных значениях параметра лямбда https: //www. mql 5. com/ru/articles/363

ПРЕОБРАЗОВАНИЕ (ТРАНСФОРМАЦИЯ) ВАРИАНТ 1 –устранение «ненормальности» ; 2 - устранение эффекта шкалы - связи между статистиками вариационного ряда; 3 - устранение неравенства варианс, или неаддитивности варианс статистических комплексов.
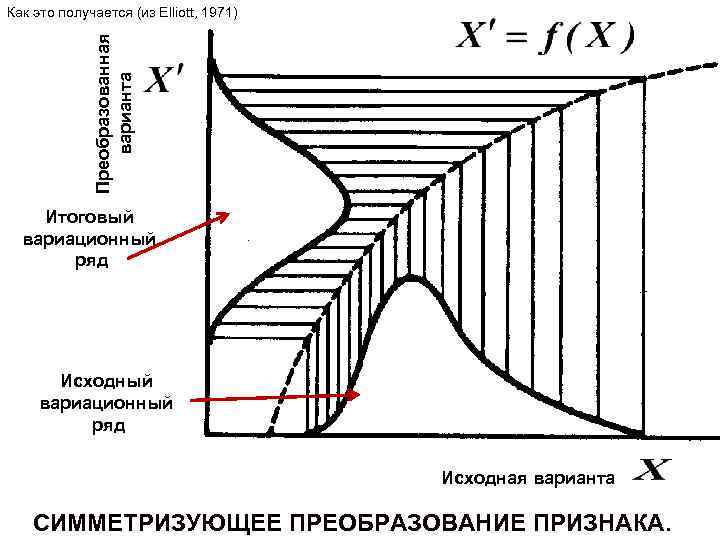
Преобразованная варианта Как это получается (из Elliott, 1971) Итоговый вариационный ряд Исходная варианта СИММЕТРИЗУЮЩЕЕ ПРЕОБРАЗОВАНИЕ ПРИЗНАКА.
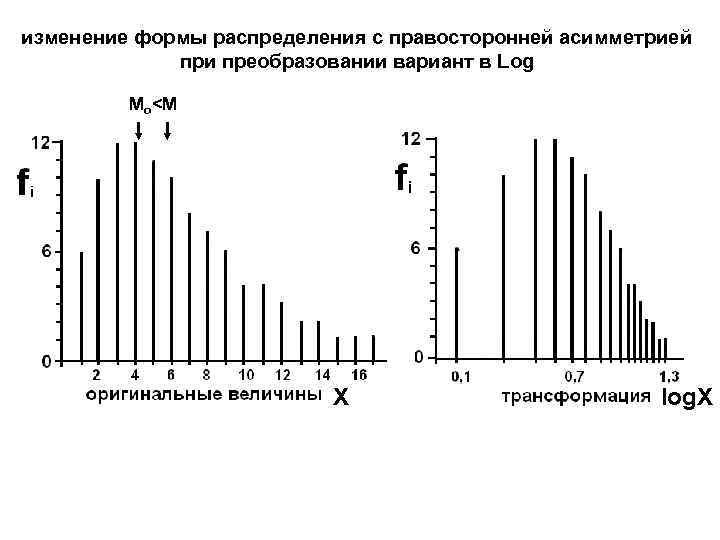
изменение формы распределения с правосторонней асимметрией при преобразовании вариант в Log Мо<М X log. X

нормализующее преобразование - преобразование, в результате которого получается переменная, распределение которой более похоже на нормальное, чем исходное. Если распределение имеет правостороннюю асимметрию, то рекомендуются преобразования вариант в…. При левосторонней асимметрии следует выбирать функции растущие быстрее линейной.

Распределение Пуассона, или s 2 = M: Исходные Трансформация Особые параметры условия s 2=M s все Xi > 10 есть Xi < 10

Модель: отрицательный бином Исходные Трансформация параметры Модель - Бином Особые условия k > 5 Модель - Бином x’ = log(x+k/2) 2<k<5 s 2>M x’ = log(x) x’ = log(x+1) все Xi>0 есть Xi=0
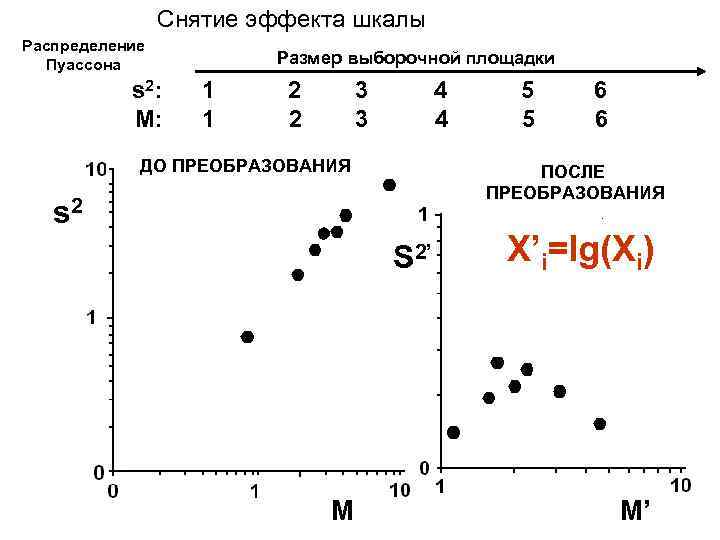
Снятие эффекта шкалы Распределение Размер выборочной площадки Пуассона s 2: 1 2 3 4 5 6 М: 1 2 3 4 5 6 ДО ПРЕОБРАЗОВАНИЯ 2 s ПОСЛЕ ПРЕОБРАЗОВАНИЯ S 2’ s 2 M М X’i=lg(Xi) M’ М

СТАБИЛИЗАЦИЯ ВАРИАНСЫ ДЛЯ СТАБИЛИЗАЦИИ ВАРИАНСЫ Р. А. ФИШЕР ПРЕДЛОЖИЛ ТРАНСФОРМАЦИЮ ВИДА . Это и есть фи-преобразование Фишера.

***методы оценивания, связанные с соблюдением нормальности распределения вариант и требующие аддитивности варианс сравниваемых совокупностей, не могут быть применены к небольшим выборкам (n<30), но приложимы к трансформированным вариантам. ***
ОБС_05_2015.ppt