ОБС 2 ОСНОВЫ БИОСТАТИСТИКИ http www hydrobiology spb

ОБС 2 ОСНОВЫ БИОСТАТИСТИКИ http: //www. hydrobiology. spb. ru БИБЛИОТЕКА Biostat-1 Biostat-2 Фото: Risto Vainola

A statistician is a professional Статистик - это профессионал, который старательно собирает who dilegently collects facts and факты и данные, а затем data and then carefully draws тщательно запутывает их них confusions about them Предмет лекции - ВЫБОРКА

ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ - бесконечно большая совокупность признаков, из которой выбирают часть для совместного изучения. ВЫБОРКА - ЧАСТЬ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ, ОТОБРАННАЯ ОПРЕДЕЛЕННЫМ СПОСОБОМ ДЛЯ ИЗУЧЕНИЯ ВАРИАЦИОННЫЙ РЯД - двойной ряд чисел, показывающий, каким образам числовые значения признака (варианты) связаны с их повторяемостью (частотой) в выборке или иной статистической совокупности (комплексе). Ранжированный вариационный ряд - это РЯД РАСПРЕДЕЛЕНИЯ.

РАСПРЕДЕЛЕНИЕ (признака) - соотношение между ранжированными значениями признака и их частотой. - соотношение между значениями признака, ранжированными в порядке возрастания величин, и частотой их встречаемости в выборке. Выборку характеризуют ВЫБОРОЧНЫЕ ПОКАЗАТЕЛИ. Генеральную совокупность характеризуют ПАРАМЕТРЫ.

- всякое общее лишь приблизительно охватывает отдельные элементы; - всякое отдельное неполно входит в общее. При создании выборки необходимо учитывать: - задачу исследования; - свойства изучаемого явления; - наши возможности по сбору и обработке данных; - специфику процедуры статистического оценивания ПРИЗНАК – свойство (показатель) , проявлением которого одна единица описания биосистемы отличается от другой, аналогичной. однородные признаки образуют ВЫБОРКУ (СТАТИСТИЧЕСКУЮ СОВОКУПНОСТЬ, СТАТИСТИЧЕСКИЙ КОМПЛЕКС).

Об. ЪЕКТЫ, ПРЕДМЕТ И ЗАДАЧИ БИОСТАТИСТИКИ ОБЪЕКТЫ – БИОСИСТЕМЫ ПРЕДМЕТ - ВАРИАЦИЯ ПРИЗНАКОВ БИОСИСТЕМ: - межгрупповая и внутригрупповая изменчивость; - морфологическая пластичность организмов, структурные и функциональные характеристики биосистем; - результаты экспериментов и приборных измерений; ……………. ЗАДАЧИ БИОСТАТИСТИКИ: - количественное описание (моделирование) биологических явлений; - исследование структуры биологических явлений; - доказательство неоднородности биологических явлений; - сжатие информации.

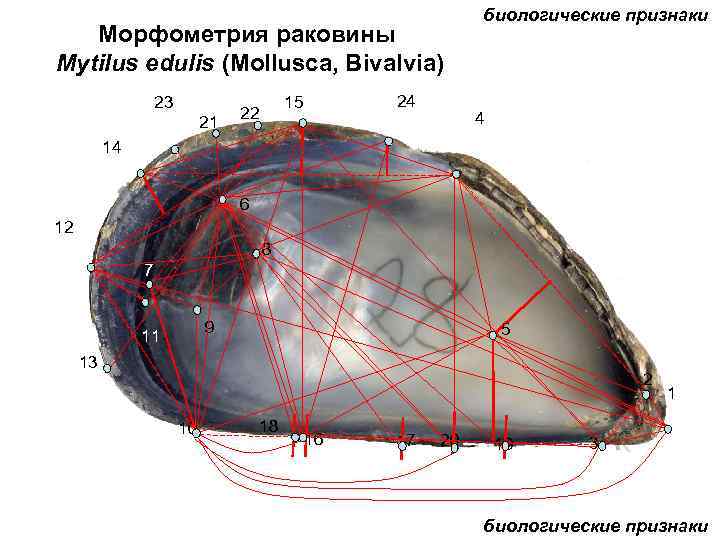
Морфометрия раковины Mytilus edulis (Mollusca, Bivalvia) 23 21 24 15 22 биологические признаки 4 14 6 12 8 7 9 11 5 13 2 10 18 16 17 20 19 1 3 биологические признаки

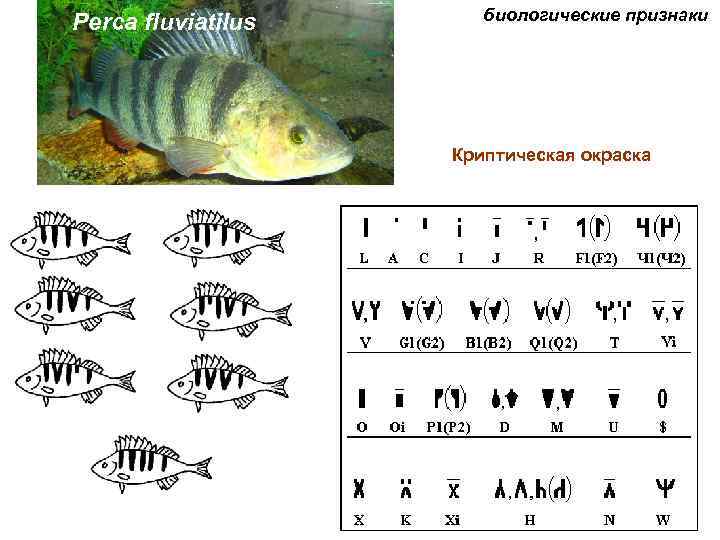
Perca fluviatilus биологические признаки Криптическая окраска

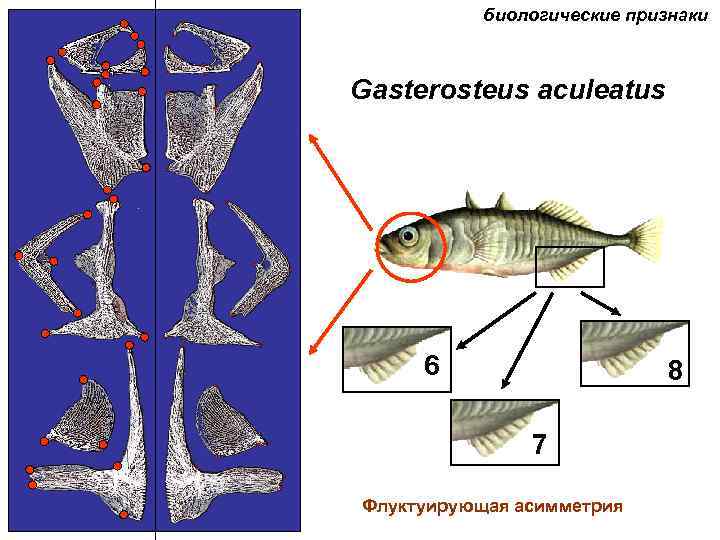
биологические признаки Gasterosteus aculeatus 6 8 7 Флуктуирующая асимметрия

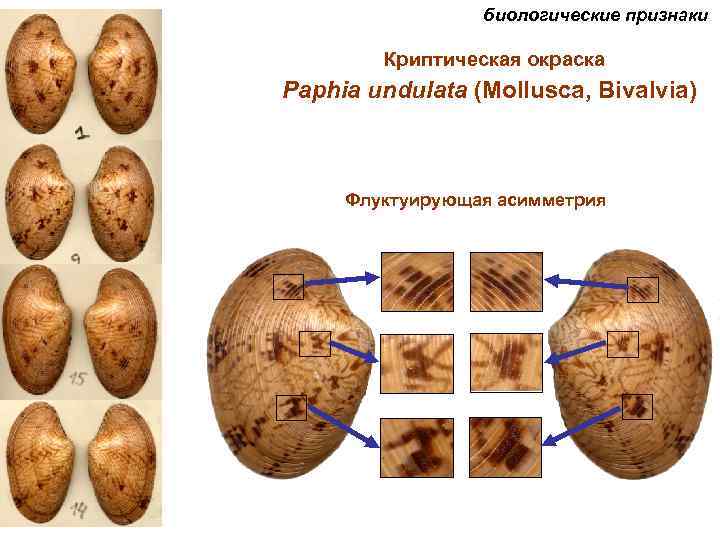
биологические признаки Криптическая окраска Paphia undulata (Mollusca, Bivalvia) Флуктуирующая асимметрия

биологические признаки Полиморфизм окраски Macoma balthica (Mollusca, Bivalvia) Фото: Сергей Добрецов Фото: Risto Vainola Luttikhuizen et all. , 2008

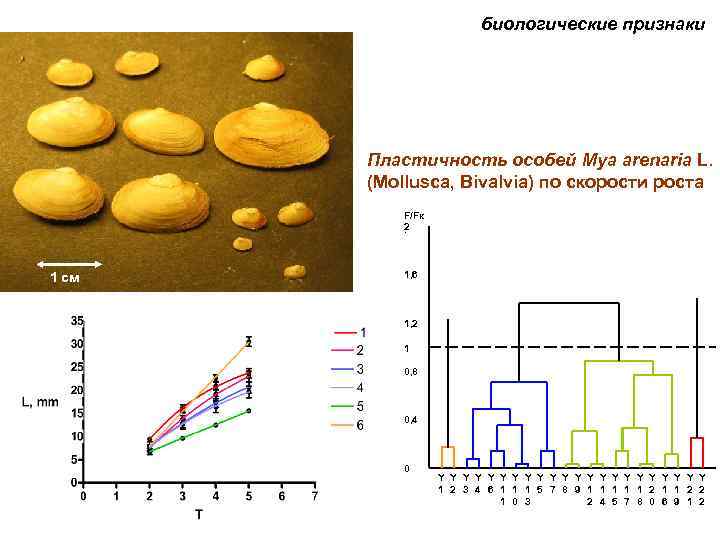
биологические признаки Пластичность особей Mya arenaria L. (Mollusca, Bivalvia) по скорости роста F/Fк 2 р 1 см 1, 6 1, 2 1 0, 8 0, 4 0 Y Y Y Y Y Y 1 2 3 4 6 1 1 1 5 7 8 9 1 1 1 2 2 1 0 3 2 4 5 7 8 0 6 9 1 2

Внутривидовая генетическая изменчивость узоров надкрылий у божьей коровки.

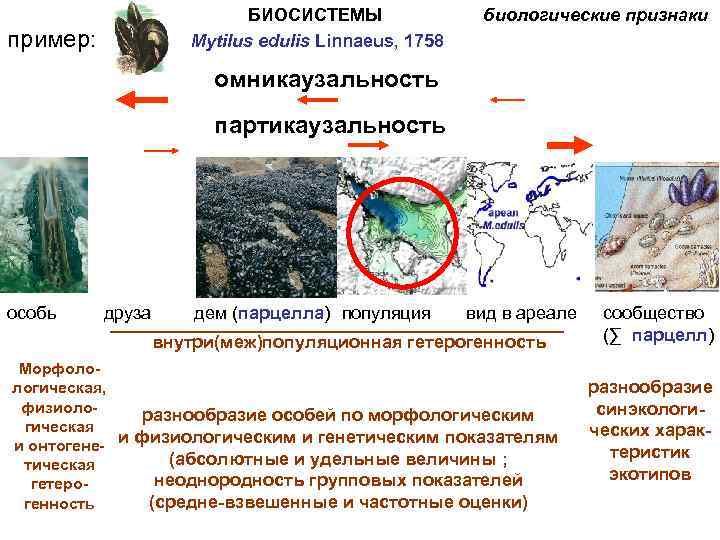
БИОСИСТЕМЫ Mytilus edulis Linnaeus, 1758 пример: биологические признаки омникаузальность партикаузальность особь друза дем (парцелла) популяция вид в ареале внутри(меж)популяционная гетерогенность Морфолологическая, физиолоразнообразие особей по морфологическим гическая и онтогене- и физиологическим и генетическим показателям (абсолютные и удельные величины ; тическая неоднородность групповых показателей гетеро(средне-взвешенные и частотные оценки) генность сообщество (∑ парцелл) разнообразие синэкологических характеристик экотипов

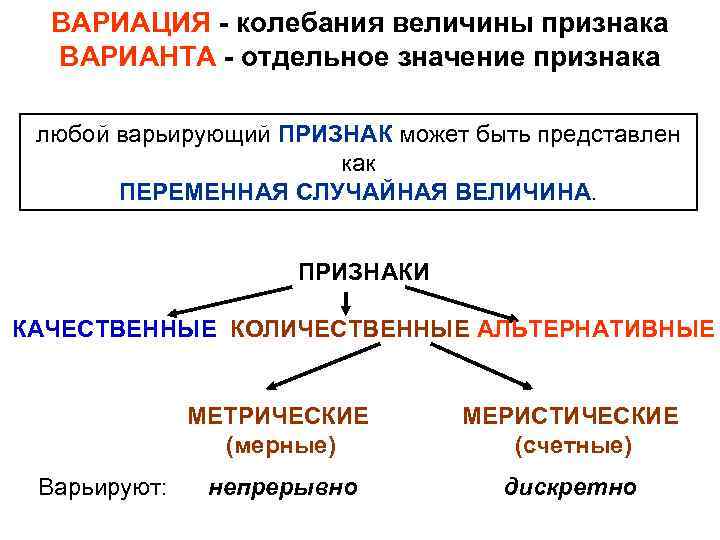
ВАРИАЦИЯ - колебания величины признака ВАРИАНТА - отдельное значение признака любой варьирующий ПРИЗНАК может быть представлен как ПЕРЕМЕННАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА. ПРИЗНАКИ КАЧЕСТВЕННЫЕ КОЛИЧЕСТВЕННЫЕ АЛЬТЕРНАТИВНЫЕ МЕТРИЧЕСКИЕ (мерные) Варьируют: непрерывно МЕРИСТИЧЕСКИЕ (счетные) дискретно

ВЫБОРОЧНЫЙ МЕТОД – статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов. Первые характеристики выборки: Хi – ВАРИАНТА (значение признака) n - ОБЪЕМ ВЫБОРКИ (число вариант) (R = Хmax - Хmin) - РАЗМАХ ВАРИАЦИИ

ВЫБОРКА ИЗ ЧЕГО? N – объем генеральной совокупности n – объем выборки

ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ (N) – бесконечное множество однородных, но индивидуально различимых объектов (показателей) ВЫБОРКА (n)– часть генеральной совокупности, отобранная определенным способом для изучения. Объем генеральной совокупности (N) по определению много больше объема выборки (n), следовательно: А) - ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ НЕ МЕНЯЕТ СВОИХ СВОЙСТВ ПРИ ИЗЪЯТИИ ВЫБОРКИ Б) - ВЫБОРКА НЕ ПОЛНОСТЬЮ ОТРАЖАЕТ ГЕНЕРАЛЬНУЮ СОВОКУПНОСТЬ И ДЛЯ ЦЕЛЕЙ БИОСТАТИСТИКИ ДОЛЖНА БЫТЬ РЕПРЕЗЕНТАТИВНОЙ, Т. Е. ПРЕДСТАВИТЕЛЬНОЙ

В РЕПРЕЗЕНТАТИВНОЙ ВЫБОРКЕ разные значения вариант представлены приблизительно с той же частотой что и в генеральной совокупности. Следовательно, выводы, основанные на изучении репрезентативной выборки, можно считать применимыми к изучаемому явлению. Такое распространение результатов анализа выборочной совокупности на все изучаемое явление называют ГЕНЕРАЛИЗУЕМОСТЬЮ.

Наше отношение к размеру выборки антропоморфно The secretary of defense gave the president his daily briefing. He concluded by saying: "Yesterday, 3 Brazilian soldiers were killed. " "Oh No!" the president exclaimed. "That's Terrible!" His staff was stunned at this display of emotion, nervously watching as the president sat, his head in his hands. Finally, the president looked up and asked, "Just how much is a brazillion? " (how many brazillians there are? )

A statistics professor was describing sampling theory to his class, explaining how a sample can be studied and used to generalize to a population. One of the students in the back of the room kept shaking his head. "What's the matter? " asked the professor. "I don't believe it, " said the student, "why not study the whole population in the first place? " The professor continued explaining the ideas of random and representative samples. The student still shook his head. The professor launched into the mechanics of proportional stratified samples, randomized cluster sampling, the standard error of the mean, and the central limit theorem. The student remained unconvinced saying, "Too much theory, too risky, I couldn't trust just a few numbers in place of ALL of them. " Attempting a more practical example, the professor then explained the scientific rigor and meticulous sample selection of the Nielsen television ratings which are used to determine how multiple millions of advertising dollars are spent. The student remained unimpressed saying, "You mean that just a sample of a few thousand can tell us exactly what over 250 MILLION people are doing? " Finally, the professor, somewhat disgruntled with the scepticism, replied, "Well, the next time you go to the campus clinic and they want to do a blood test. . . tell them that's not good enough. . . tell them to TAKE IT ALL!!"

Как организовать выборку? СХЕМЫ ОТБОРА ПОКАЗАТЕЛЕЙ (ПРОБ) (наиболее распространенная классификация) 1. ПРОСТОЙ СЛУЧАЙНЫЙ; 2. ТИПИЧЕСКИЙ (СТРАТИФИЦИРОВАННЫЙ) 3. СЕРИЙНЫЙ 4. МЕХАНИЧЕСКИЙ 5. РАЗЛИЧНЫЕ СОЧЕТАНИЯ ИЗ 1, 2, 3 и 4

Как организовать выборку? Пример классификации выборок на одном из сайтов ПРОСТАЯ СЛУЧАЙНАЯ ВЫБОРКА ТИПИЧЕСКАЯ (СТРАТИФИЦИРОВАННАЯ) ВЫБОРКА СЕРИЙНАЯ (ГНЕЗДОВАЯ) ВЫБОРКА МЕХАНИЧЕСКАЯ ВЫБОРКА КОМБИНИРОВАННАЯ ВЫБОРКА МНОГОСТУПЕНЧАТАЯ ВЫБОРКА . . .

Как организовать выборку? Ситуация 1. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ (ИЗУЧАЕМОЕ ЯВЛЕНИЕ) a priori НЕ МОЖЕТ БЫТЬ ДИФФЕРЕНЦИРОВАНА ПО КАЧЕСТВЕННЫМ ПРИЗНАКАМ 1. ПРОСТАЯ ВЫБОРКА

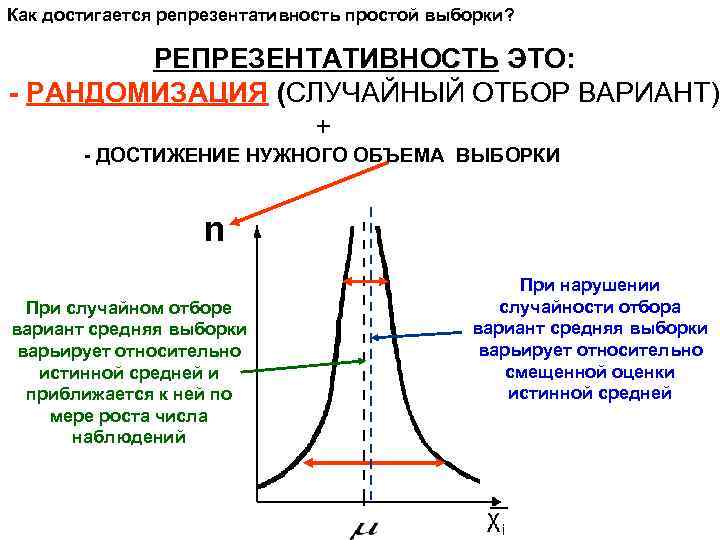
Как достигается репрезентативность простой выборки? РЕПРЕЗЕНТАТИВНОСТЬ ЭТО: - РАНДОМИЗАЦИЯ (СЛУЧАЙНЫЙ ОТБОР ВАРИАНТ) + - ДОСТИЖЕНИЕ НУЖНОГО ОБЪЕМА ВЫБОРКИ n При случайном отборе вариант средняя выборки варьирует относительно истинной средней и приближается к ней по мере роста числа наблюдений При нарушении случайности отбора вариант средняя выборки варьирует относительно смещенной оценки истинной средней

Как достигается репрезентативность простой случайной выборки? Выборка называется СЛУЧАЙНОЙ, если она: 1. Построена таким образом, что каждое значение признака в пределах совокупности имеет равные возможности быть отобранным для анализа. 2. Сформирована так, что любое сочетание из значений изучаемого признака имеет равные возможности быть отобранным для анализа.

Как достигается репрезентативность простой случайной выборки? СПОСОБЫ ОТБОРА ВАРИАНТ (ПРОБ): ПОВТОРНЫЙ и БЕСПОВТОРНЫЙ 1. - ПОЛНОСТЬЮ СЛУЧАЙНЫЙ (МЕТОД ЖЕРЕБЬЁВКИ) 2. - РЕГУЛЯРНЫЙ (МЕХАНИЧЕСКИЙ)

ПРИМЕР Задача: Изучение поселения Mya arenaria БЕСПОВТОРНЫЙ ПОЛНОСТЬЮ СЛУЧАЙНЫЙ ОТБОР ПРОБ n = 10 0. 25 м 2

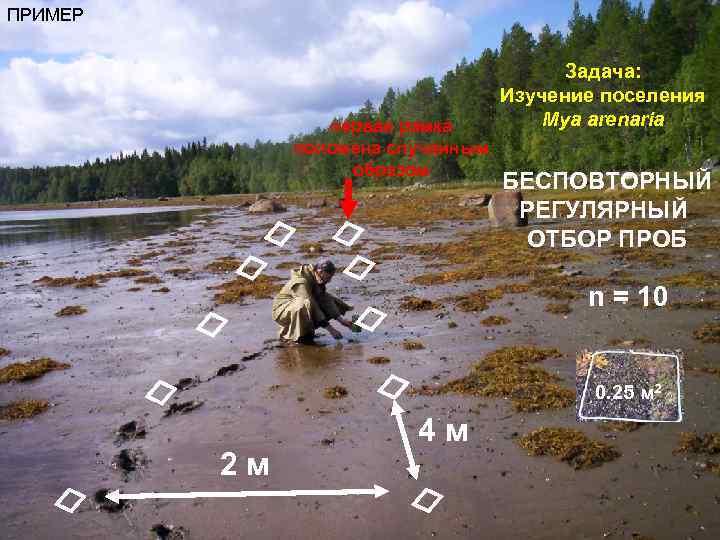
ПРИМЕР первая рамка положена случайным образом Задача: Изучение поселения Mya arenaria БЕСПОВТОРНЫЙ РЕГУЛЯРНЫЙ ОТБОР ПРОБ n = 10 0. 25 м 2 2 м 4 м

2. МЕХАНИЧЕСКИЙ ОТБОР ПРОБ показатели для статистического анализа собираются производится через равномерные промежутки (алфавит, временная шкала, пространственная шкакла. . . ), так что генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице. ПРОСТАЯ СЛУЧАЙНАЯ ВЫБОРКА

ПРИМЕР Задача: Изучение поселения Mya arenaria БЕСПОВТОРНЫЙ РЕГУЛЯРНЫЙ (механический) ОТБОР ПРОБ n = 10 0. 25 м 2

Как организовать выборку? Ситуация 2. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ (ИЗУЧАЕМОЕ ЯВЛЕНИЕ) АПРИОРИ МОЖЕТ БЫТЬ ДИФФЕРЕНЦИРОВАНА ПО КАЧЕСТВЕННЫМ ПРИЗНАКАМ Гетеротопность местообитания вида, характер распределения фонообразующих видов, изменения рельефа, градации пременных среды, градации условий эксперимента (опыта), структура биосистем (возрастная структура популяции) и тп.

Как организовать выборку? Пример: ОТБОР ПРОБ ПО СХЕМЕ (ЭКСПЕРИМЕНТ) 3. ТИПИЧЕСКИЙ (СТРАТИФИЦИРОВАННЫЙ) предполагает разделение очевидно неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному качественному признаку, после чего из каждой выделенной части берут ПРОСТУЮ СЛУЧАЙНУЮ ВЫБОРКУ. СТАТИСТИЧЕСКИЙ КОМПЛЕКС

4. СЕРИЙНЫЙ (ГНЕЗДОВОЙ) генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение. СТАТИСТИЧЕСКИЙ КОМПЛЕКС

ПРОБА - единичное испытание; - единичное измерение; - значение показателя. - плотность поселения; - половой состав; - биомасса; - число видов и др. ВЫБОРКА - показателей морфометрии особей вида. 0. 25 м 2

О необходимой точности измерений ACCURACY - ТОЧНОСТЬ, В СМЫСЛЕ ПОЛНОЕ СООТВЕТСТВИЕ ПОКАЗАТЕЛЯ ДАННОМУ ОБРАЗЦУ PRECISION (ПРЕЦИЗИОННОСТЬ) ВАРИАНТ БЛИЗОСТЬ ЗНАЧЕНИЙ ВАРИАНТ ВЫБОРКИ ДРУГУ правило округления: 6, 285 --> 6, 29 6, 275 --> 6, 27. Адекватность (validity) процедуры измерения Мы называем процедуру измерения адекватной, если она измеряет именно то, что мы собираемся измерять.

ТРЕБОВАНИЯ К КАЧЕСТВУ СТАТИСТИЧЕСКИХ НАБЛЮДЕНИЙ И ОЦЕНОК 1. Размерность статистических оценок должна соответствовать размерности вариант. Телефонный звонок: - Алло, это квартира Сидорова Ивана Петровича? - Нет, это квартира Каца Абрама Самуиловича. - Извините, это 22 -38 -89? - Нет, это 22 -38 -88. - Надо же! Ошибка в шестом знаке, а такой эффект

ТРЕБОВАНИЯ К КАЧЕСТВУ СТАТИСТИЧЕСКИХ НАБЛЮДЕНИЙ И ОЦЕНОК 2. Каждое наблюдение (измерение) должно быть однозначным (чистым), т. е. объективным, свободным от домыслов. A politician travelling in Scotland looked out of the window and saw a number of black sheep. «That’s Interesting» he said, «all Scottish sheep are black» . «No, no, » warned his agent. «Don’t make positive statements like that. Best just say ‘Some Scottish sheep are black’. Isn’t that right, Jan? » Jan, a statistician, replied, «Well, on the evidence so far, the only thing you can say is: Some Scottish sheep are black on one side»

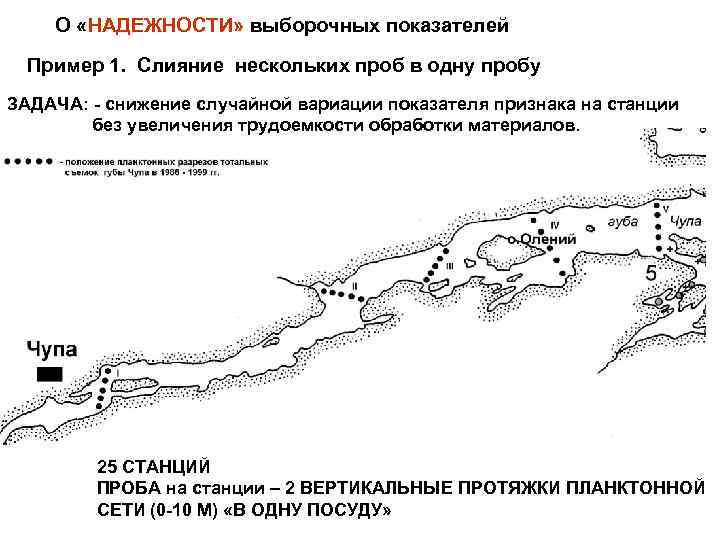
О «НАДЕЖНОСТИ» выборочных показателей Пример 1. Слияние нескольких проб в одну пробу ЗАДАЧА: - снижение случайной вариации показателя признака на станции без увеличения трудоемкости обработки материалов. 25 СТАНЦИЙ ПРОБА на станции – 2 ВЕРТИКАЛЬНЫЕ ПРОТЯЖКИ ПЛАНКТОННОЙ СЕТИ (0 -10 М) «В ОДНУ ПОСУДУ»

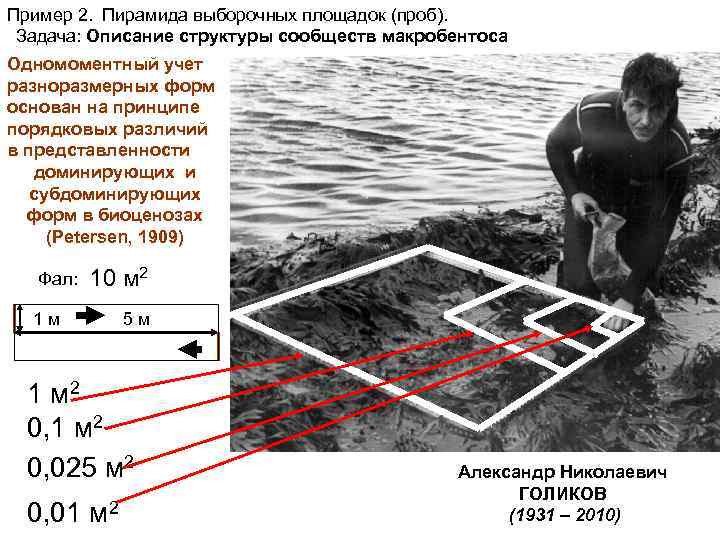
Пример 2. Пирамида выборочных площадок (проб). Задача: Описание структуры сообществ макробентоса Одномоментный учет разноразмерных форм основан на принципе порядковых различий в представленности доминирующих и субдоминирующих форм в биоценозах (Petersen, 1909) Фал: 10 м 2 1 м 5 м 1 м 2 0, 025 м 2 0, 01 м 2 Александр Николаевич ГОЛИКОВ (1931 – 2010)

Забегая вперед ПРИНЦИПЫ ПЛАНИРОВАНИЯ ПРОБООТБОРА ПРИ СОЗДАНИИ ВЫБОРОЧНЫХ КОМПЛЕКСОВ: 1 - ОБЪЕМЫ СРАВНИВАЕМЫХ ВЫБОРОК ДОЛЖНЫ БЫТЬ ОДИНАКОВЫМИ; 2 - ПРИ УЧЕТЕ ОРГАНИЗМОВ В УЧЕТНОЙ ПЛОЩАДКЕ В СРЕДНЕМ ДОЛЖНО ОКАЗАТЬСЯ НЕ МЕНЕЕ 10 ОСОБЕЙ ИЗУЧАЕМОГО ВИДА; 3 - СЛЕДУЕТ СТРЕМИТЬСЯ К МИНИМИЗАЦИИ ВАРИАНСЫ И (ИЛИ) ВЫРАВНИВАНИЯ ЕЁ ЗНАЧЕНИЙ ПО ВСЕМ СРАВНИВАЕМЫМ ВЫБОРКАМ

Лирическое отступление Понятие «КОНЕЧНАЯ ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ» Используется в экономике, социологии и тп. Пример: Имеем: мастерская – шесть станков – один обслуживающий инженер. Интересует: вероятность поломки одного станка за время t. После поломки 1, 2 или более станков этот показатель будет меняться (уменьшаться).

СПОСОБЫ ПРЕДСТАВЛЕНИЯ ДАННЫХ ДЛЯ СТАТ. АНАЛИЗА ЧЕТЫРЕХПОЛЬНАЯ ТАБЛИЦА. ------------------- Курс Обнаружено: ВСЕГО: больных здоровых 1 40 65 105 2 35 71 106 ВСЕГО: 75 136 211 -------------------

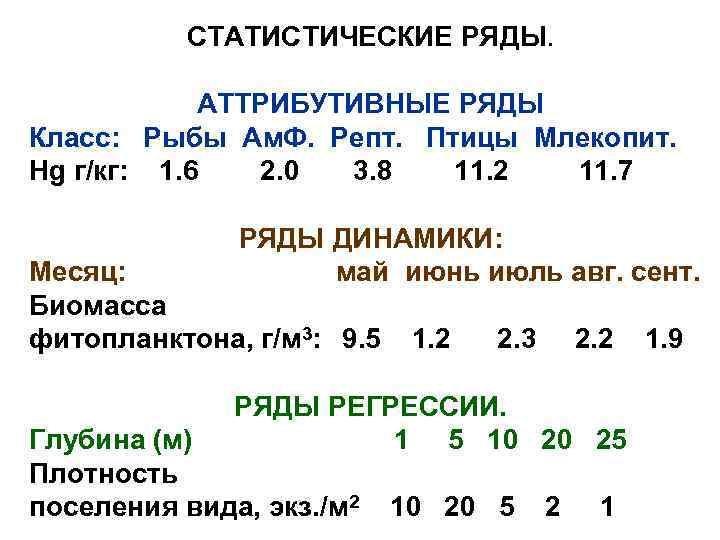
СТАТИСТИЧЕСКИЕ РЯДЫ. АТТРИБУТИВНЫЕ РЯДЫ Класс: Рыбы Ам. Ф. Репт. Птицы Млекопит. Нg г/кг: 1. 6 2. 0 3. 8 11. 2 11. 7 РЯДЫ ДИНАМИКИ: Месяц: май июнь июль авг. сент. Биомасса фитопланктона, г/м 3: 9. 5 1. 2 2. 3 2. 2 1. 9 РЯДЫ РЕГРЕССИИ. 1 5 10 20 25 Глубина (м) Плотность поселения вида, экз. /м 2 10 20 5 2 1

ВАРИАЦИОННЫЙ РЯД МЕТРИЧЕСКИЕ (мерные) признаки - основа для построения НЕПРЕРЫВНЫХ ВАРИАЦИОННЫХ РЯДОВ, а МЕРИСТИЧЕСКИЕ – используются для построения ДИСКРЕТНЫХ ВАРИАЦИОННЫХ РЯДОВ. 1. Дискретный вариационный ряд - это вариационный ряд, построенный с использованием признака, принимающего только конечное число определенных значений. Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака.

Построение дискретного вариационного ряда ВЫБОРКА 4 6 10 7 7 5 9 8 4 6 6 5 7 9 8 6 7 7 5 8 6 7 5 7 ВЗВЕШЕННЫЙ РЯД: варианты Xi. . . 4 6 10 7 5 9 8 частота (вес) вариант. . 2 5 1 8 4 2 3 относительные частоты (%)- 8 28 4 32 16 8 12 ВЗВЕШЕННЫЙ РАНЖИРОВАННЫЙ РЯД РАСПРЕДЕЛЕНИЯ Xi (варианты). . . 4 5 6 7 8 9 10 Fi (частоты)…. . . 2 4 5 8 3 2 1

Построение непрерывного вариационного ряда КЛАССЫ (КЛАССОВЫЕ ИНТЕРВАЛЫ) РАВНОИНТЕРВАЛЬНЫЕ или НЕРАВНОИНТЕРВАЛЬНЫЕ - ширина К - число классов = (Хmax - Хmin)/К. 1. К = 12 3. 2. Правило Старджеса: n = 2(k+1). К = 1 + 3. 32 lg(n) 3. (Доерфель, 1969). 4. При n>100 К 5. К = 5*lg(n) (Шторм, 1979). = 0, 6 s, где s – среднее квадратическое отклонение.

Построение непрерывного вариационного ряда ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ К ОПРЕДЕЛЕНИЮ ОПТИМАЛЬНОГО ДЛЯ СТАТИСТИЧЕСКОГО АНАЛИЗА ЧИСЛА КЛАССОВ n k 40– 100 7– 9 100– 500 8– 12 500– 1000 10– 16 1000– 10000 12– 22 (ВНИИ Метрологии )

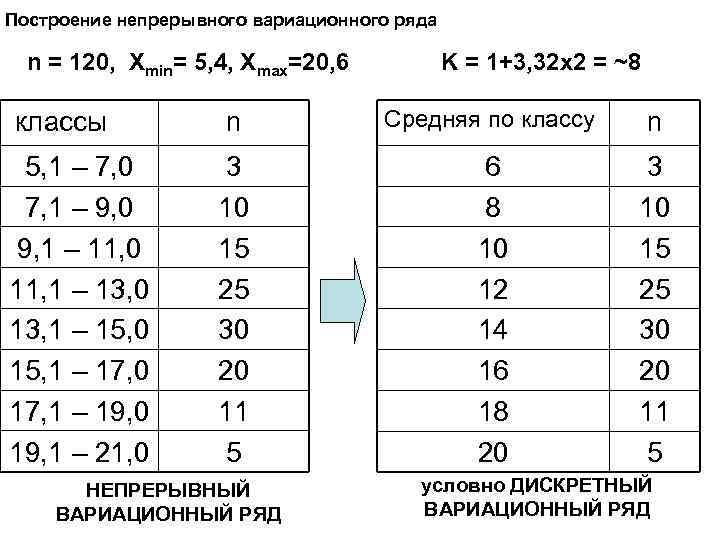
Построение непрерывного вариационного ряда n = 120, Xmin= 5, 4, Xmax=20, 6 K = 1+3, 32 x 2 = ~8 классы n Средняя по классу n 5, 1 – 7, 0 7, 1 – 9, 0 9, 1 – 11, 0 11, 1 – 13, 0 13, 1 – 15, 0 15, 1 – 17, 0 17, 1 – 19, 0 19, 1 – 21, 0 3 10 15 25 30 20 11 5 6 8 10 12 14 16 18 20 3 10 15 25 30 20 11 5 НЕПРЕРЫВНЫЙ ВАРИАЦИОННЫЙ РЯД условно ДИСКРЕТНЫЙ ВАРИАЦИОННЫЙ РЯД

Пример вопроса из анкеты: Чем достигается репрезентативность выборки? : - увеличением V объема выборки - случайным пробоотбором - увеличением размера выборочной площадки