Обратные тригонометрические функции
Содержание: 1. Обратные тригонометрические функции, свойства, графики. 2. Преобразование выражений, содержащих обратные тригонометрические функции.
Arcsin х Арксинусом числа m называется такой угол x, для которого sinx=m, π/2≤X≤π/2, |m|≤ 1 Функция y = sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей. График обратной функции симметричен с графиком основной функции относительно биссектрисы I - III координатных углов.
![Свойства функции y = arcsin x 1)Область определения: отрезок [ -1; 1]; 2)Область изменения:](https://present5.com/presentation/169287036_227497290/image-4.jpg "Свойства функции y = arcsin x 1)Область определения: отрезок [ -1; 1]; 2)Область изменения:")
Свойства функции y = arcsin x 1)Область определения: отрезок [ -1; 1]; 2)Область изменения: отрезок [-π/2, π/2]; 3)Функция y = arcsin x нечетная: arcsin (-x) = - arcsin x; 4)Функция y = arcsin x монотонновозрастающая; 5)График пересекает оси Ох, Оу в начале координат.
Arccos х Арккосинусом числа m называется такой угол x, для которого: cos x = m 0≤x≤π |m|≤ 1
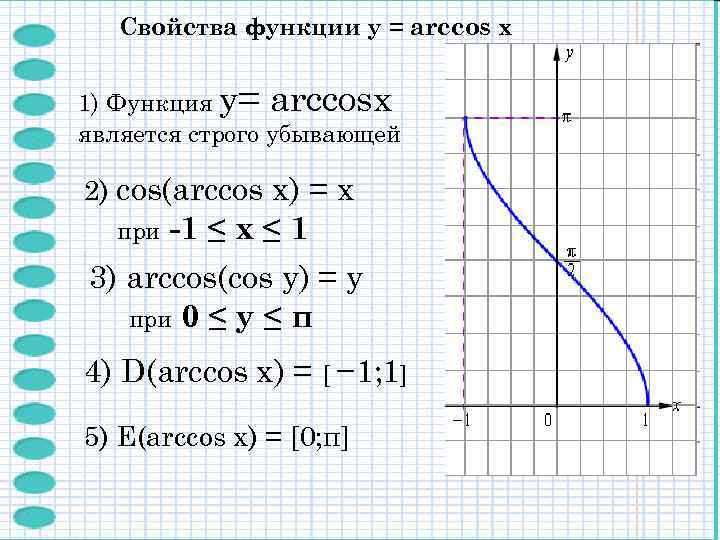
Свойства функции y = arccos x 1) Функция y= arccosx является строго убывающей 2) cos(arccos x) = x при -1 ≤ х ≤ 1 3) arccos(cos y) = y при 0 ≤ y ≤ π 4) D(arccos x) = [ − 1; 1] 5) E(arccos x) = [0; π]
Arctgх Арктангенсом числа m называется такой угол x, для которого tgx=m, -π/2<X<π/2. График функции y=arctgx получается из графика Функции y=tgx, симметрией относительно прямой y=x.
![y=arctgх 1) Область определения: х є R 2) Область значения: отрезок [-π/2, π/2]; 3)](https://present5.com/presentation/169287036_227497290/image-8.jpg "y=arctgх 1) Область определения: х є R 2) Область значения: отрезок [-π/2, π/2]; 3)")
y=arctgх 1) Область определения: х є R 2) Область значения: отрезок [-π/2, π/2]; 3) Функция y = arctg x - нечетная: arctg (-x) = - arctg x; 4) Функция y = arctg x монотонно-возрастающая; 5) График пересекает оси Ох, Оу в начале координат. y yx
Arcctgх Арккотангенсом числа m называется такой угол x, для которого ctgx = a, 0<x<π
Arcctgх 1) Функция y = arcctg x непрерывна и ограничена на всей своей числовой прямой. 2) Функция y = arcctg x является строго убывающей. 3) ctg(arcctg x) = x, при xєR 4) arcctg(ctg y) = y, при 0 < y < π 5) D(arcctg x) = (-∞; ∞) 6) E(arcctg x) = (0; π)
Скачать презентацию Обратные тригонометрические функции Содержание 1 Обратные тригонометрические
198586.ppt