Обработка результатов наблюдений Лямин Андрей Владимирович
Определения Множество возможных значений случайной величины X называется генеральной совокупностью или пространством выборки. Множество измеренных значений (x 1, x 2, …xn) случайной величины называется выборкой, где n – объем выборки. Любая функция зависящая от наблюдений называется статистикой.
Вариационный ряд Вариационным рядом называется последовательность элементов выборки, расположенных в неубывающем порядке. Минимальный xmin и максимальный xmax элементы выборки называются крайними. Разность R= xmax- xmin называется размахом.
Пример 1: • {0, -2, 3, -1, -4, 0, 1, 2, -2} • {-4, -2, -1, 0, 0, 1, 2, 2, 3, 3} • xmin=-4, xmax=3, R=7
Точечные оценки Точечной оценкой числовой характеристики генеральной совокупности называется статистика приближенно равная . Оценка называется состоятельной, если для любого >0 Оценка называется несмещенной, если
Оценки средних значений, дисперсии, корреляции
Пример 2: Последовательность случайных чисел: {0. 42, 0. 52, 0. 33, 0. 43, 0. 23, 0. 58, 0. 76, 0. 53, 0. 64, 0. 21} Оценка математического ожидания: 0. 48. Оценка дисперсии: 0. 07.
Математическое ожидание оценки дисперсии
Принцип максимального правдоподобия
Пример 3:
Интервальные оценки Доверительным интервалом числовой характеристики генеральной совокупности с доверительной вероятностью называется интервал ( 1, 2) со случайными границами 1= = 1(x 1, x 2, …xn), 2= 2(x 1, x 2, …xn), который накрывает с вероятностью : P( 1< < 2)= , где =1 - – уровень значимости.
Построение интервальной оценки для среднего значения
Построение интервальной оценки для среднего значения
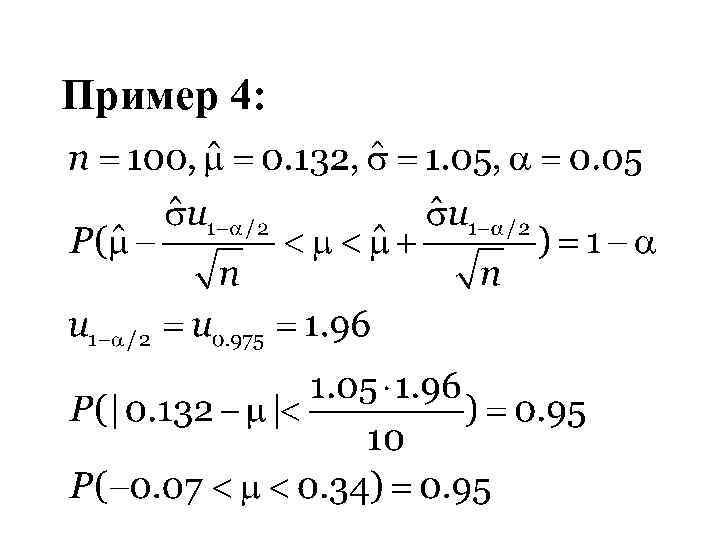
Пример 4:
Пример 5:
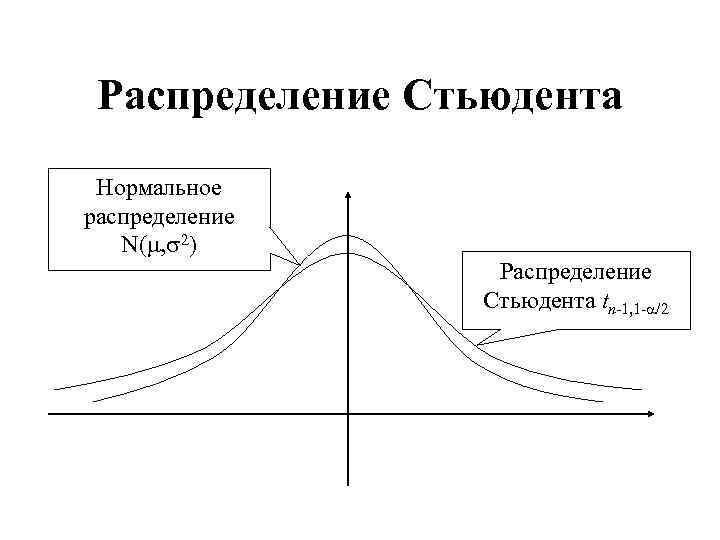
Распределение Стьюдента Нормальное распределение N( , 2) Распределение Стьюдента tn-1, 1 - /2
Статистические гипотезы Статистической гипотезой называется предположение о виде и свойствах генерального и выборочного распределений. Критерием значимости называется правило проверки статистической гипотезы. Статистикой критерия значимости Z называется функция наблюдений, по значениям которой судят о справедливости гипотезы.
Статистические гипотезы Критической областью критерия называется подмножество Vk множества V значений статистки Z, вероятность попадания в которое при условии истинности гипотезы равна уровню значимости 0, т. е. P(Z Vk)=. Множество VVk называется областью допустимых значений статистики критерия.
Схема проверки гипотез 1. Выдвигается проверяемая гипотеза H 0 и ей альтернативная H 1. 2. Выбирается уровень значимости (0. 1, 0. 05, 0. 01, 0. 001). 3. Выбирается статистика Z, строится критическая область Vk и область допустимых значений VVk. 4. Вычисляется выборочное значение статистики. 5. Если Z Vk, гипотеза H 0 отвергается, иначе – принимается.
Мощность критерия • Мощностью критерия называется вероятность отклонения гипотезы H 0, когда она ложна. • Ошибка первого рода – отклонение гипотезы H 0, когда она верна. • Ошибка второго рода – принятие гипотезы H 0, когда она ложна.
Проверка гипотез с помощью доверительных интервалов Гипотеза H 0: = 0 принимается, если построенный доверительный интервал покрывает 0, и отвергается в противном случае.
Пример 6:
Метод гистограмм
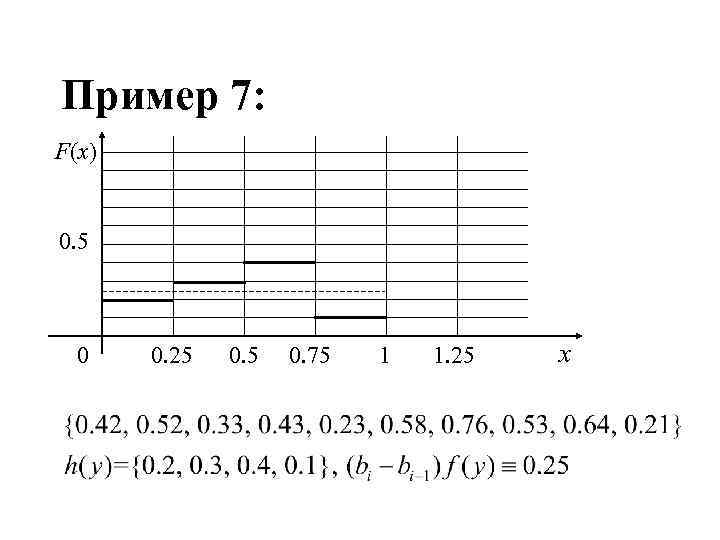
Пример 7: F(x) 0. 5 0 0. 25 0. 75 1 1. 25 x
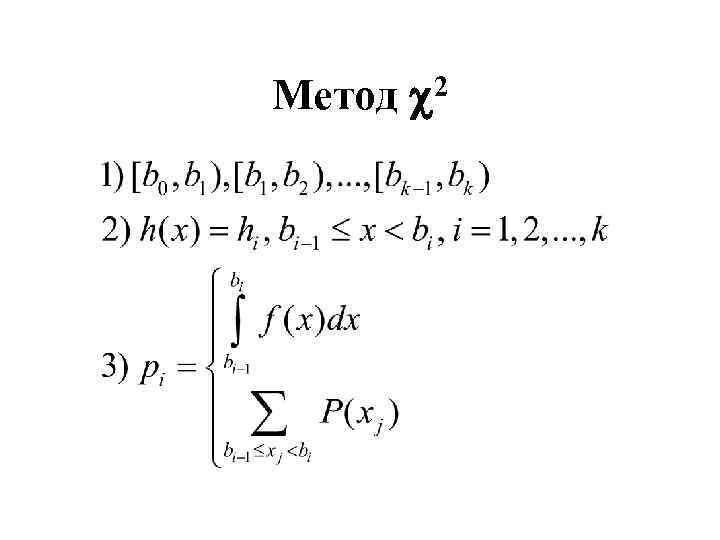
Метод 2
Метод 2
Пример 8:
Скачать презентацию Обработка результатов наблюдений Лямин Андрей Владимирович Определения
lect_03_01.ppt