2.3 Системы счисления 2011.pptx
- Количество слайдов: 33

ОБРАБОТКА ИНФОРМАЦИИ • Источниками и носителями информации могут быть сигналы любой природы: речь, музыка, текст, показания приборов и т. д. Однако хранение, передача и переработка информации в ее естественном физическом виде большей частью неудобна, а иногда и просто невозможна. В таких случаях применяется кодирование.

Кодирование • Кодирование - это процесс установления взаимно однозначного соответствия элементам и словам одного алфавита элементов и слов другого алфавита. • Кодом называется правило, по которому сопоставляются различные алфавиты и слова.

Системы счисления • Системой счисления называется способ записи чисел при помощи ограниченного числа символов (цифр). • Позиционной системой счисления называется система счисления, при которой число, связанное с цифрой, зависит от места, которое она занимает.

Позиционные системы счисления-1 • Позиционные системы счисления — это те системы счисления, в которых значение цифры напрямую зависит от её положения в числе. • Они позволяют легко производить арифметические расчёты

Позиционные системы счисления-2 • Количество цифр используемых в системе счисления называется «основанием» . • В десятичной системе основание равно десяти, в двоичной системе основание равно двум, в восьмеричной и шестнадцатеричной соответственно восьми и шестнадцати. • То есть в b-ичной системе счисления количество цифр равно b и используются цифры от 0 до b -1.

Позиционные системы счисления-3 • В общем случае в позиционной системе счисления числа представляются следующим образом: • (anan − 1. . . a 0)f, где a 0, a 1, . . . , an — цифры, а f — основание системы счисления. Если используется десятичная система, то f — можно опустить

Позиционные системы счисления-3 • Под позиционной системой счисления обычно понимается b-ичная система счисления, которая определяется целым числом b > 1, называемым основанием системы счисления.

. Целое число x в b-ичной системе счисления представляется в виде конечной линейной комбинации степеней числа b: где ak — это целые числа, называемые цифрами, удовлетворяющие неравенству

Пример • Примером позиционной формы записи чисел является та, которой мы пользуемся (так называемая арабская форма чисел). • Так, в числах 123 и 321 значения цифры 3, например, определяются ее положением в числе: в первом случае она обозначает три единицы (т. е. просто три), а во втором – три сотни (т. е. триста)

• Число x записывают в виде последовательности его b-ичных цифр, перечисляемых по убыванию старшинства разрядов слева направо: • Например, число сто три представляется в десятичной системе счисления в виде:
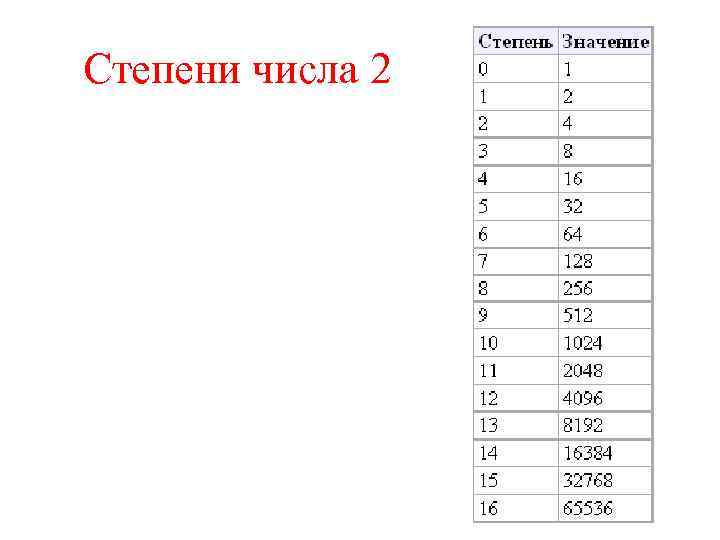
Степени числа 2

Непозиционные системы счисления • Римские числа являются примером полупозиционной системы образования числа: так, в числах IX и XI знак I обозначает в обоих случаях единицу, но, будучи расположенным слева от знака X (обозначающего десять), вычитается из десяти, а при расположении справа – прибавляется к десяти. В первом случае полное значение числа равно 9, во втором – 11.

Полное число В современной информатике используются в основном три системы счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная. где l – количество разрядов числа, i – порядок разряда, m – основание системы счисления, ai – множитель, принимающий любые целочисленные значения от 0 до m-1, и соответствующий цифре i-го порядка числа.

Примеры чисел • 110012 — число в двоичной системе счисления, a 0 = 1, a 1 = 0, a 2 = 0, a 3 = 1, a 4 = 1; • 2213 — число в троичной системе счисления, a 0 = 1, a 1 = 2, a 2 = 2; • 318 — число в восьмеричной системе счисления, a 0 = 1, a 1 = 3; • 2510 — число в десятичной системе счисления, a 0 = 5, a 1 = 2;

Преобразование чисел • Чему равны числа из примеров. Используем приведённую формулу:

Пример • Представление чисел с помощью арабских цифр — самая распространённая позиционная система счисления, она называется «десятичной системой счисления» . • Десятичной системой она называется потому, что использует десять цифр. Эти цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Как получить число? • У нас есть некоторое число A, и мы хотим получить его представление в системе по основанию f. Как нам это сделать? • Число A можно представить в виде (anan − 1. . . a 0)f, и остаток от деления a 0.

Почему a 0? • Все члены суммы делятся на f без остатка, а последний член a 0 в результате деления даёт 0 и a 0 в остатке, так как максимальное значение цифры всегда на единичку меньше основания системы. • Мы получили самую правую цифру a 0 как остаток от деления и число (anan − 1. . . a 1)f как результат деления числа A на f. • Если мы так будем продолжать делить, то получим все остальные цифры a 1, a 2. . . an.

Пример • Получим число 25 в двоичной системе счисления: • 25 / 2 = 12, остаток 1 – а 0; • 12 / 2 = 6, остаток 0 –а 1; • 6 / 2 = 3, остаток 0 -а 2; • 3 / 2 = 1, остаток 1 -а 3; • 1 / 2 = 0, остаток 1 -а 4. • Получили: 110012.

Пример • Представим число 25 в троичной системе счисления: • 25 / 3 = 8, остаток 1; • 8 / 3 = 2, остаток 2; • 2 / 3 = 0, остаток 2. • Получили число: 2213

Пример • . Для восьмеричной и десятичной систем счисления Десятичная система Восьмеричная счисления: система счисления: • 25 / 10 = 2, 25 / 8 = 3, остаток 1; остаток 5; 3 / 8 = 0, остаток 3. • 2 / 10 = 0, остаток 2. Результат: 318. Результат: 2510.

Пример • Чтобы лучше понять перевод в различные системы счислений, посмотрим, какие трансформации происходят внутри числа 456710. • Представим это число в виде • . • • • Последовательно разделим на 10: делим на 10, получаем и 7 в остатке; делим ещё раз на 10, получаем и 6 в остатке; и ещё раз делим на 10, получаем 4 и 5 в остатке; делим в последний раз на 10, получаем 0 и 4 в остатке.

Шестнадцатеричная система • Шестнадцатеричная система счисления используется для кодирования дискретного сигнала. Используемые знаки для представления числа – десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F. • для обозначения шестнадцатеричных чисел вводят нижний индекс справа от числа в виде числа 16 или букв H либо h (hexadecimal – шестнадцатеричный), либо знак H или h справа от числа. • Например, 3 AB 16 = 3 ABH = 3 ABh

Восьмеричная и шестнадцатеричная системы счислений • Компьютерам очень удобно оперировать двоичными числами, но люди не привыкли работать с большим количеством цифр. Например, чтобы представить в двоичном виде число 1234 потребуется больше 10 двоичных цифр (10011010010). • Поэтому были придуманы восьмеричная и шестнадцатеричная системы счислений. Они удобны как и десятичные числа тем, что для представления числа требуется меньшее количество разрядов. А по сравнению с десятичными числами, перевод в двоичное представление очень простой. Это как будто мы двоичное число разбили на группы по три или четыре разряда и каждой двоичной комбинации придумали значок.

Таблицы 8 -ричных и 16 -ричных цифр

Таблица перевода трех систем счисления

Перевод чисел из одной системы счисления в другую • Для перевода чисел из одной системы счисления в другую существуют определенные правила. Они различаются в зависимости от формата числа – целое или правильная дробь. • Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби.

Алгоритм перевода • При переводе чисел из десятичной системы счисления в систему с основанием P > 1 обычно используют следующий алгоритм: • 1) если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;

Алгоритм перевода (продолжение) • 2) если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т. д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после запятой в порядке их получения.

Алгоритм перевода (продолжение) • Результатом может быть либо конечная, либо периодическая дробь в системе счисления с основанием P. • Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P.

Примеры • 1. Перевести данное число из десятичной системы счисления в двоичную: а) 464(10); б) 380, 1875(10); в) 115, 94(10) (получить пять знаков после запятой в двоичном представлении). • Решение. • 464 | 0 380 | 0 |1875 115 | 1 |94 • 232 | 0 190 | 0 0|375 57 | 1 1|88 • 116 | 0 95 | 1 0|75 28 | 0 1|76 • 58 | 0 47 | 1 1|5 14 | 0 1|52 • а) 29 | 1 б) 23 | 1 1|0 в) 7 | 1 1|04 • 14 | 0 11 | 1 3 | 1 0|08 • 7 | 1 5 | 1 1 | 1 0|16 • 3 | 1 2 | 0 • 1 | 1 а) 464(10) = 111010000(2); б) 380, 1875(10) = 101111100, 0011(2); в) 115, 94(10) » 1110011, 11110(2)

Перевод числа 10011010010 (1234) 2 • Разбиваем его на группы по три цифры: • 010 011 010. • И по таблице переводим: 23228. • Чтобы перевести число в шестнадцатеричное представление разбиваем двоичное число на группы по четыре цифры: • 0100 1101 0010. • И по таблице переводим: 4 D 216.

Шестидесятеричная система счисления • Время на часах – это пример шестидесятеричной позиционной системы счисления. • В представлении времени используется три позиции: для часов, минут и секунд • h: m: s • Чтобы получить время в секундах мы должны посчитать по формуле: • h 602 + m 601 + s 600 = h 3600 + m 60 + s
2.3 Системы счисления 2011.pptx