Лк_2 Обраб_эксп.pptx
- Количество слайдов: 19

Обработка экспериментальных данных

Компьютерная интерполяция Интерполяцией называется представление функции y=f(x), заданной аналитически или в виде таблицы функцией y=φ(x), идентичной исходной в некоторой области аргумента. Основные этапы компьютерной интерполяции: 1. Выбор вида функции интерполяции, 2. Определение коэффициентов функции интерполяции, 3. Оценка адекватности функции интерполяции.
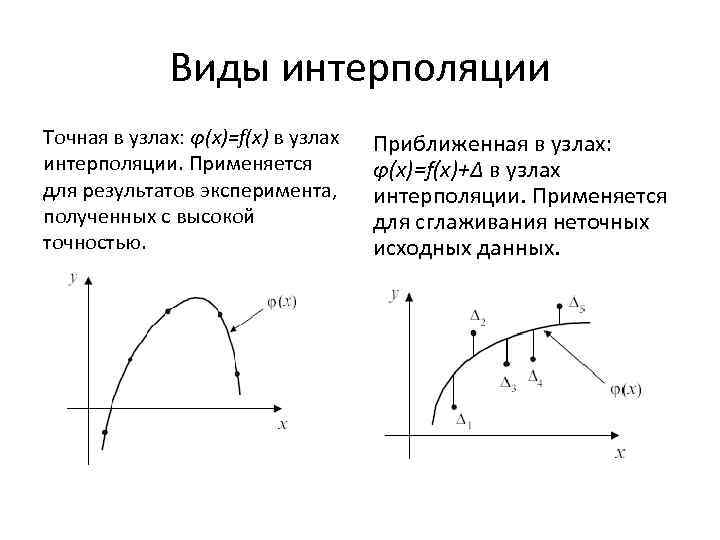
Виды интерполяции Точная в узлах: φ(x)=f(x) в узлах интерполяции. Применяется для результатов эксперимента, полученных с высокой точностью. Приближенная в узлах: φ(x)=f(x)+Δ в узлах интерполяции. Применяется для сглаживания неточных исходных данных.

Критерии близости исходной и интерполирующей функций • Равенство нулю алгебраической суммы уклонений, • Минимальна сумма квадратов уклонений, • Минимально среднее значение уклонений.

Способы выбора функции интерполяции Функция интерполяции φ(x) определяет математическую модель изучаемого объекта или явления. Способы выбора: 1. Графо-аналитический метод, 2. Метод линеаризации нелинейных функций, 3. Метод табличных разностей, 4. Обращение к специальным программам автоматизации выбора.
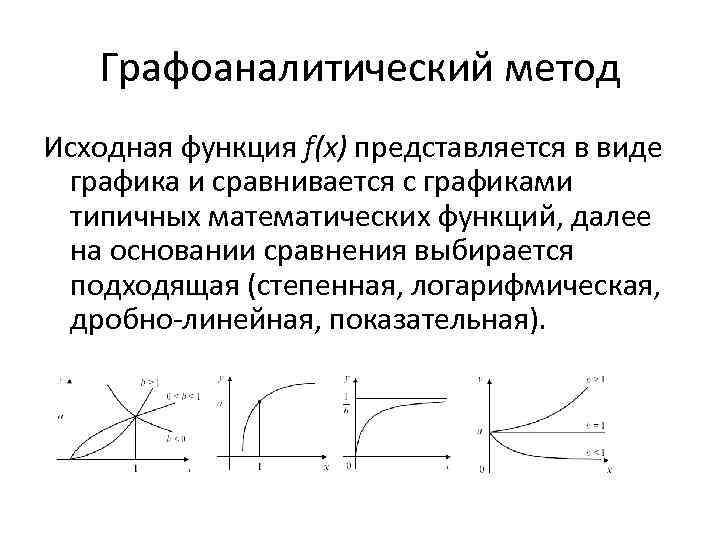
Графоаналитический метод Исходная функция f(x) представляется в виде графика и сравнивается с графиками типичных математических функций, далее на основании сравнения выбирается подходящая (степенная, логарифмическая, дробно-линейная, показательная).

Линеаризация нелинейных функций Осуществляется путем представления их в иной системе координат методом замены переменных х и у. Например, степенная функция представляется в виде , где Y=lny, X=lnx. После такой подстановки определение коэффициентов для функции φ(x) производится с помощью методов, применяемых для линейных функций.

Анализ табличных разностей Способ позволяет определить степень интерполирующего полинома. Если n-е табличные разности функции y=f(x) одинаковы, то степень полинома будет не выше n.

Обращение к специальным программам автоматизации выбора Существуют программные средства, позволяющие выбрать функцию интерполяции для исходной, заданной в табличной форме. Например, SIMPLE FORMULA, Table. Curve, Curve Expert. Результат их использования – тысячи функций с указанной погрешностью.

Определение коэффициентов функции интерполяции. Выбор метода определения коэффициентов зависит от типа функции, требуемой точности и возможностей используемого программного пакета. Особенности применения системы Mathcad 1. При использовании некоторых методов откликом является не искомая функция, а ее численные значения для заданных значений аргумента. 2. Результатом решения задачи интерполяции является массив коэффициентов функции, а не ее аналитическое выражение.

Определение адекватности интерполирующей функции • Табулирование функции: вычисление значений функций φ(x) в узлах интерполяции; • Графическое сравнение функций φ(x) и f(x), выполненных в одной координатной системе; • Определение погрешности или показателя корреляции.

Критерии адекватности интерполирующей функции Критерием близости функций φ(x) и f(x) может быть: 1. Абсолютная среднеквадратичная погрешность (ε); 2. Относительная среднеквадратичная погрешность (δ); Полученная функция φ(x) считается адекватной, если расчетная погрешность меньше допустимой. 3. Коэффициент корреляции для линейной интерполяции (r), 4. Индекс корреляции для нелинейных зависимостей (γ). Чем ближе показатель корреляции к единице, тем ближе экспериментальные точки располагаются к линии y=φ(x)

Линейная интерполяция Функция φ(x)=ax+b Функция f(x) задана двумя векторами Vx и Vy. Определение значений коэффициентов c помощью стандартных функций: intercept (Vx, Vy) =a slope (Vx, Vy) =b line (Vx, Vy) = Функция для расчета коэффициента корреляции: corr(Vx, Vy) = r

Полиномиальная интерполяция Функция f(x) задана двумя векторами Vx и Vy. Для определения коэффициентов функции φ(x) используется команда regress (Vx, Vy, k), где k степень искомого полинома. Для вычисления значения функции φ(x) в некоторой точке t используется команда interp (s, Vx, Vy, t), где s – вектор коэффициентов, найденный с помощью команды regress. Стандартная функция для вычисления индекса корреляции отсутствует.

Интерполяция одной из стандартных функций Функция f(x) задана двумя векторами Vx и Vy. Можно подобрать φ(x) в виде одной из стандартных функций: expfit(Vx, Vy, Vg) – lgsfit(Vx, Vy, Vg) – sinfit(Vx, Vy, Vg) – pwrfit(Vx, Vy, Vg) – logfit(Vx, Vy, Vg) – lnfit(Vx, Vy, Vg) – Vg – вектор, задающий начальное приближение параметров а, b, c.

Интерполяция линейной комбинацией функций Функция f(x) задана двумя векторами Vx и Vy Для определения коэффициентов φ(x) используется стандартная функция linfit(Vx, Vy, F), где F – вектор функций в символьном виде.

Интерполяция произвольной нелинейной функцией Функция f(x) задана двумя векторами Vx и Vy. Можно подобрать φ(x) в виде одной произвольной функции с помощью команды: genfit(Vx, Vy, Vg, F), где Vg – вектор начальных приближений для всех неизвестных, F – вектор предлагаемой функции и ее частных производных по всем неизвестным.

Методы интерполяции точной в узлах • Решение системы линейных уравнений относительно искомых коэффициентов с помощью команд lsolve и Find. Число уравнений должно обеспечивать нахождение единственного решения. Для решения системы с помощью команды lsolve необходимо записать матрицу значений и матрицу-вектор значений Vy. Для решения системы с помощью команды Find необходимо задать начальное приближение искомых коэффициентов и записать соответствующие уравнения.

Интерполяция сплайном • Сплайном степени n называется функция вида • Для вычисления коэффициентов сплайнов используются следующие функции: lspline (Vx, Vy) – для линейного сплайна pspline (Vx, Vy) – для квадратичного сплайна cspline (Vx, Vy) – для кубического сплайна. • После нахождения коэффициентов можно определить значения в любой точке сплайна, используя функцию interp. • Позволяет получить полное совпадение в узлах интерполяции. Результатом сплайн-интерполяции является таблица, а не модель. Не обеспечивает сглаживание ошибок измерения.
Лк_2 Обраб_эксп.pptx