Журов_Лекция_12_2012.ppt
- Количество слайдов: 35

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ • интерполяция • регрессия или сглаживание • сглаживание с фильтрацией данных 1

Линейная интерполяция Функция linterp Обращение к функции linterp(x, y, t), где x - вектор опытных значения аргумента, y - вектор опытных значений функции, t - значение аргумента, при котором вычисляется интерполирующее значение функции. 2

Линейная интерполяция экспериментальных данных 3

Линейная интерполяция экспериментальных данных 4
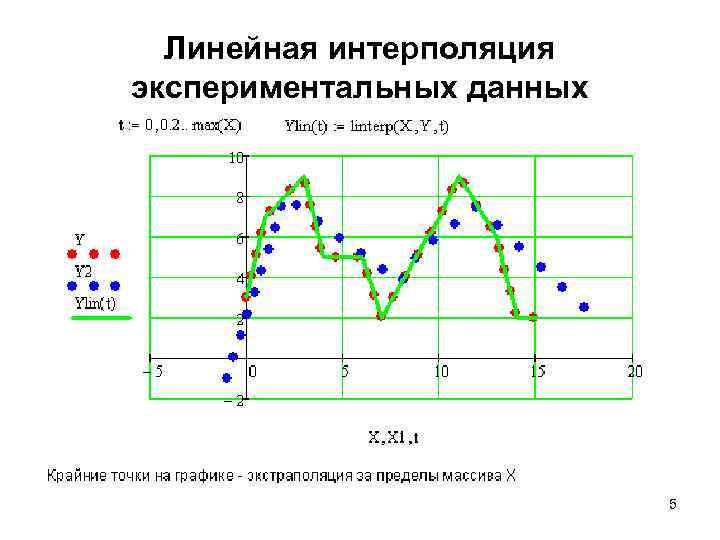
Линейная интерполяция экспериментальных данных 5
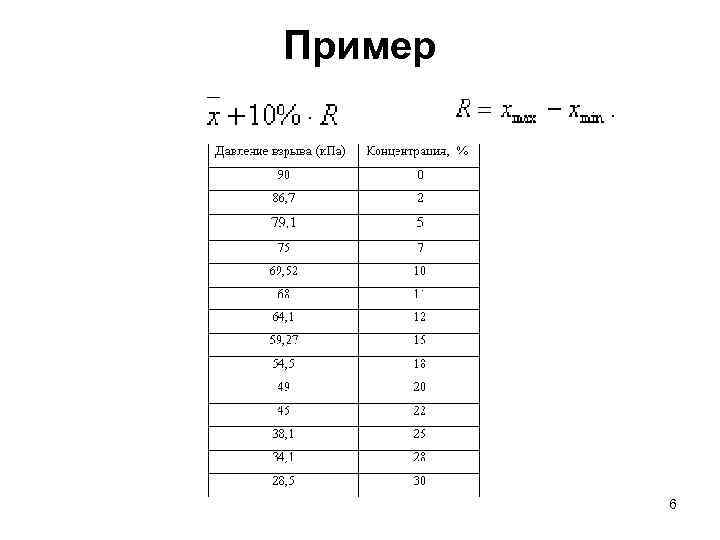
Пример 6

7
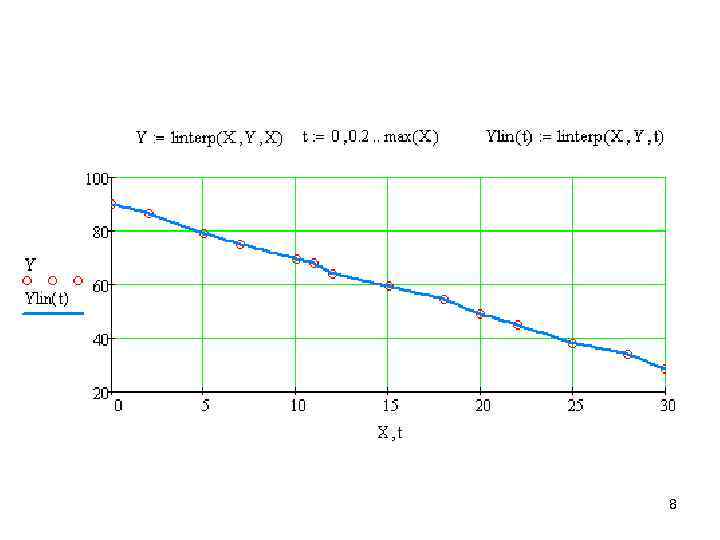
8

Кубическая сплайн-интерполяция Функция interp Обращение к функции interp(vs, X, Y, t) , где vs - вектор вторых производных, созданный одной из трех функций: lspline(X, Y), pspline(X, Y), cspline(X, Y) X - вектор опытных значений аргумента, расположенных в порядке возрастания, Y - вектор опытных значений функции, t - значение аргумента, при котором вычисляется интерполирующее значение функции. 9

Сравнение различных видов интерполяции 10
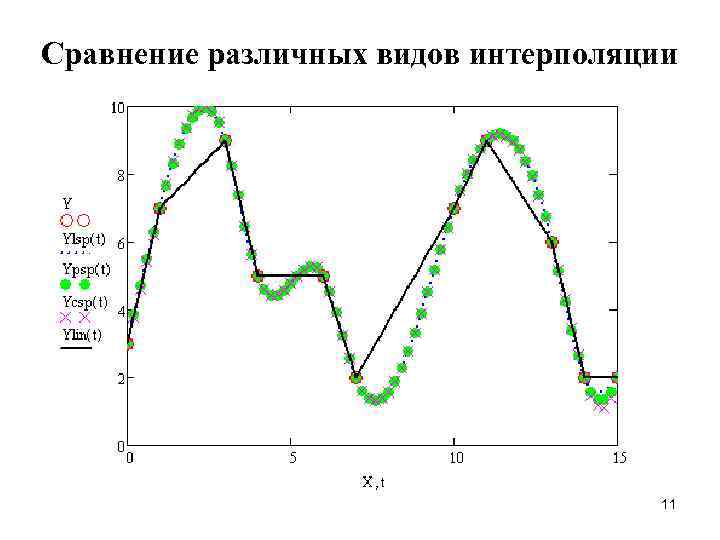
Сравнение различных видов интерполяции 11

Интерполяция В-сплайнами Функция bspline Обращение к функции bspline(X, Y, XX, n), где X - вектор опытных значений аргумента, расположенных в порядке возрастания, Y - вектор опытных значений функции, XX - вектор значений аргумента, при которых вычисляются интерполирующие значения функции, n - порядок полиномов сплайнинтерполяции (1, 2 или 3). 12
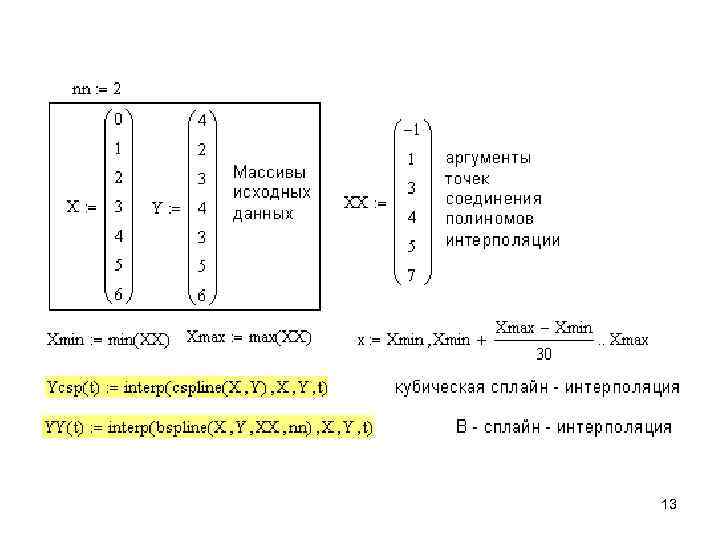
13
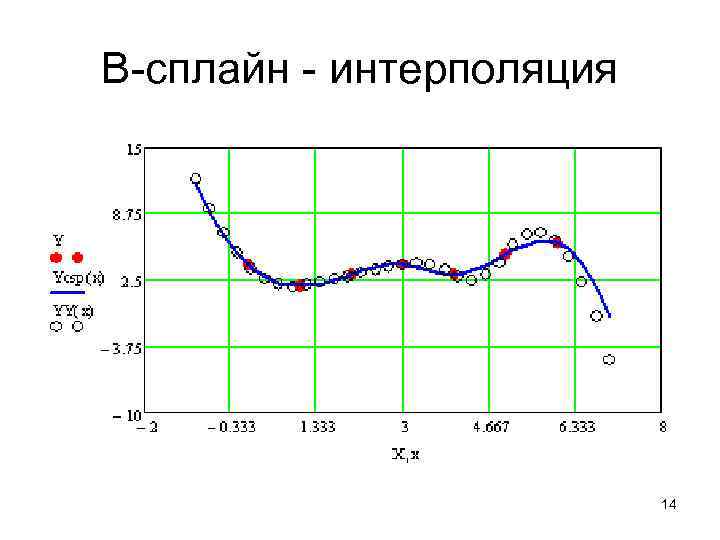
B-сплайн - интерполяция 14

Полиномиальная регрессия Функция regress В Mathcad регрессия с использованием одного полинома реализуется комбинацией встроенных функций регрессии и интерполяции interp(s, x, y, t) и regress(x, y, n), Обращение к указанным функциям: s=regress(X, Y, n) YY(t)=interp(s, X, Y, t) или YY(t)=interp(regress(X, Y, n), X, Y, t) где x - вектор значений аргумента, элементы которого расположены в порядке возрастания, y - вектор значений функции того же размера, s - вектор коэффициентов для построения апроксимирующего полинома, создаваемый функцией regress, t - значение аргумента, при котором вычисляется интерполирующая функция, n - степень аппроксимирующего полинома. 15

Полиномиальная регрессия Функция loess Регрессия с использованием нескольких отрезков полинома реализуется комбинацией встроенных функций регрессии и интерполяции interp(s, X, Y, t) и loess(X, Y, L), где s=loess(X, Y, L) - вектор коэффициентов для построения апроксимирующего полинома второй степени, требуемый функцией interp, L>0 - параметр, определяющий размер отрезков полиномов. 16
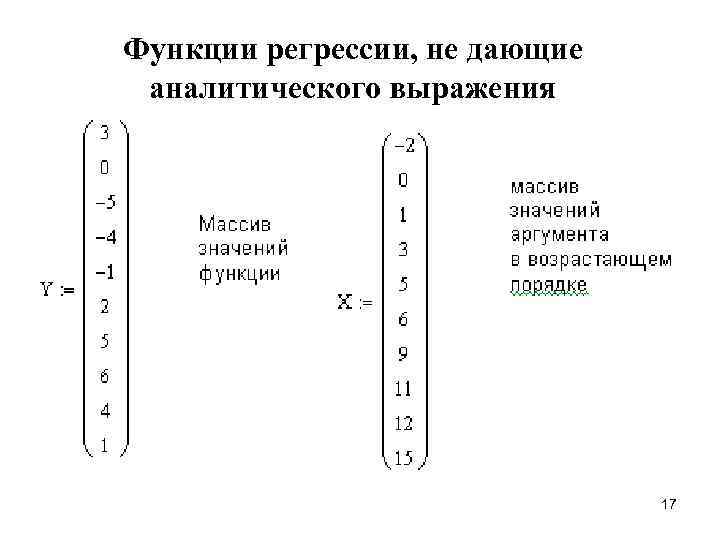
Функции регрессии, не дающие аналитического выражения 17

Функции регрессии, не дающие аналитического выражения 18
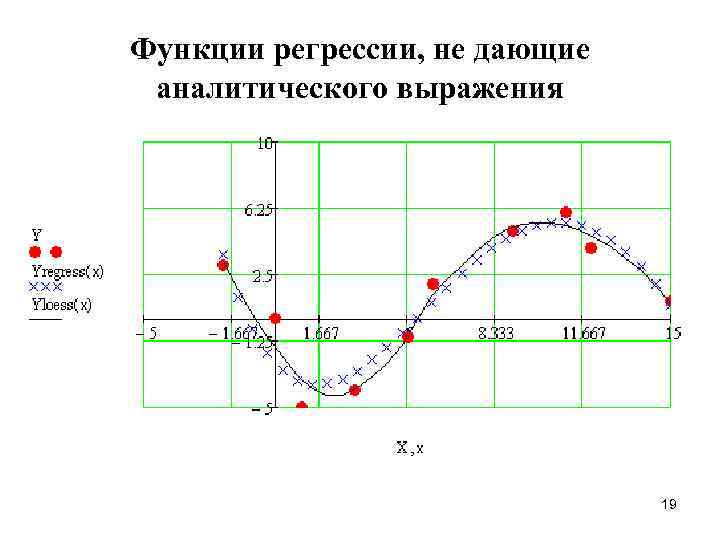
Функции регрессии, не дающие аналитического выражения 19

Функции регрессии, дающие аналитические выражения • expfit(X, Y, g) – • sinfit(X, Y, g) • pwrfit(X, Y, g) – • lgsfit(X, Y, g) – • logfit(X, Y, g) – 20
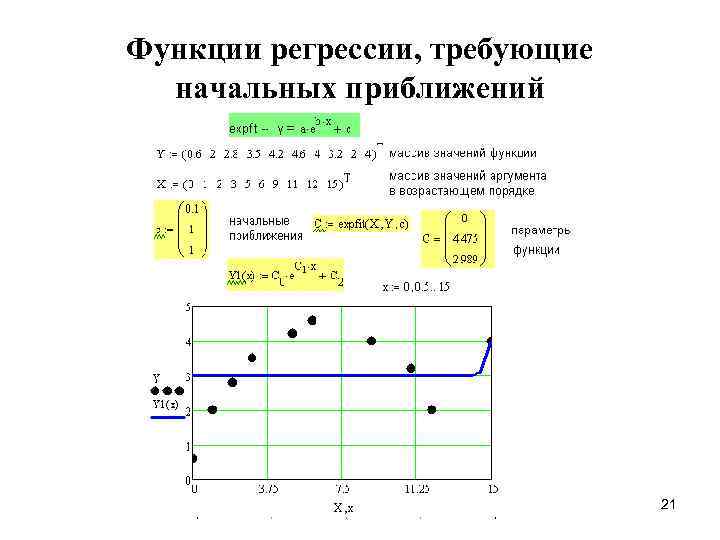
Функции регрессии, требующие начальных приближений 21
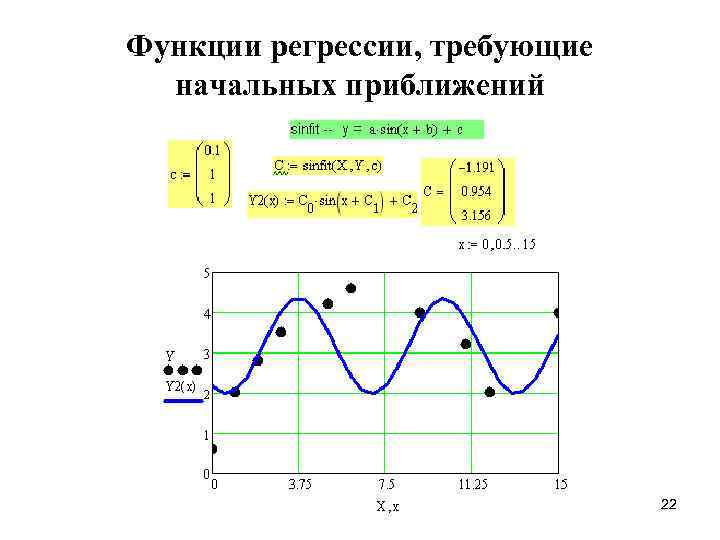
Функции регрессии, требующие начальных приближений 22
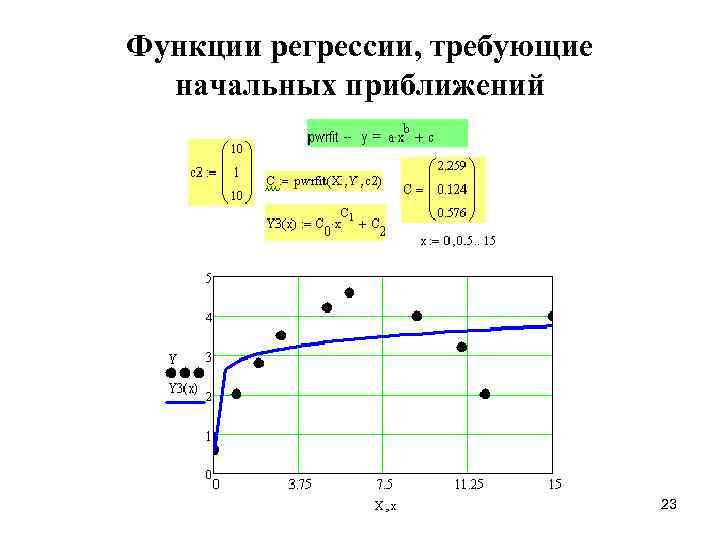
Функции регрессии, требующие начальных приближений 23
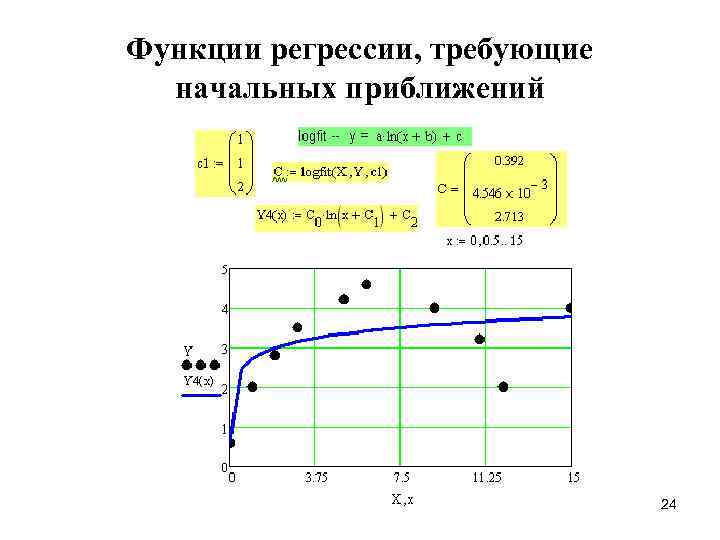
Функции регрессии, требующие начальных приближений 24
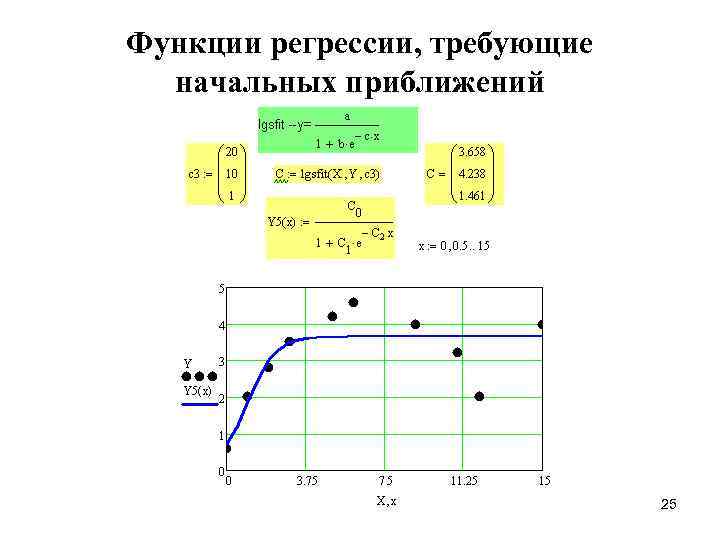
Функции регрессии, требующие начальных приближений 25
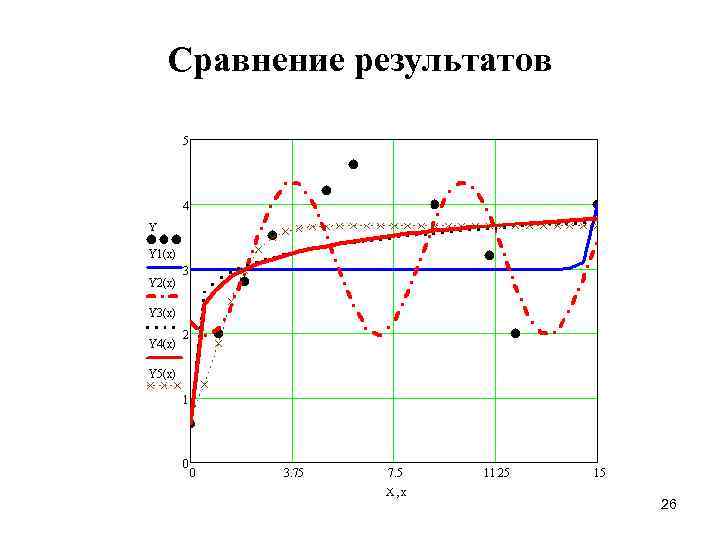
Сравнение результатов 26

Функции регрессии, не требующие начальных приближений • line(X, Y) – • medfit(X, Y) – • lnfit(X, Y) – 27

Функции регрессии, не требующие начальных приближений 28
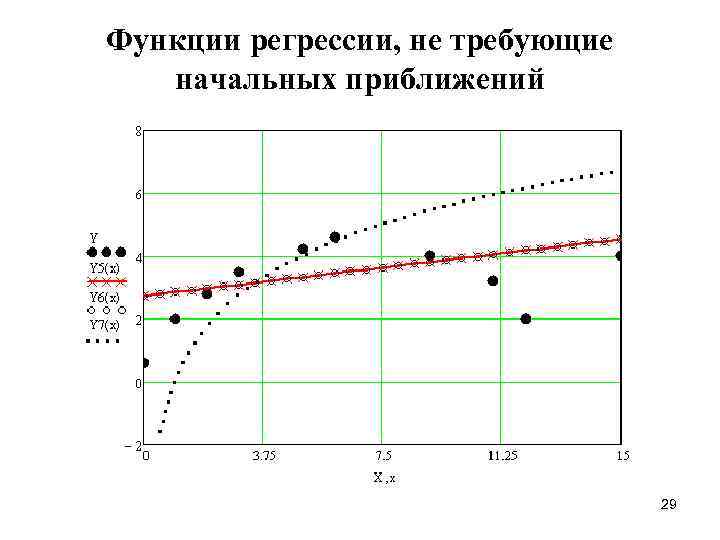
Функции регрессии, не требующие начальных приближений 29

Обобщенная регрессия • linfit(x, y, F) • genfit(x, y, C, F) 30

31

32
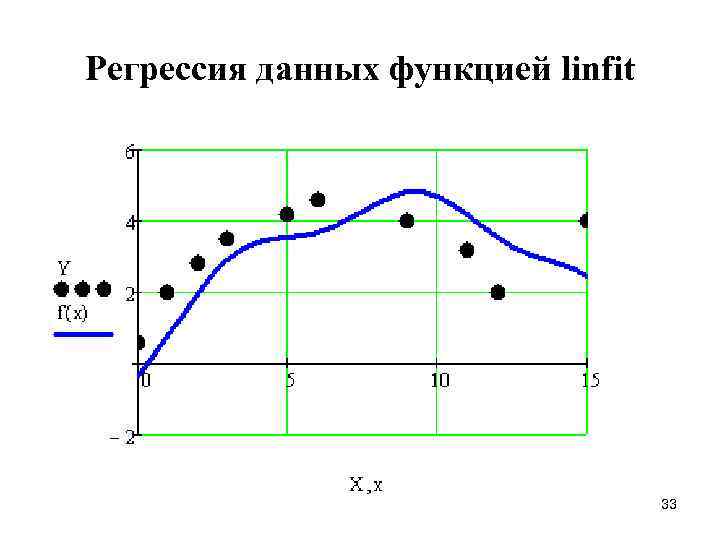
Регрессия данных функцией linfit 33

Нелинейная регрессия общего вида с помощью функции genfit(X, Y, C, F) 34
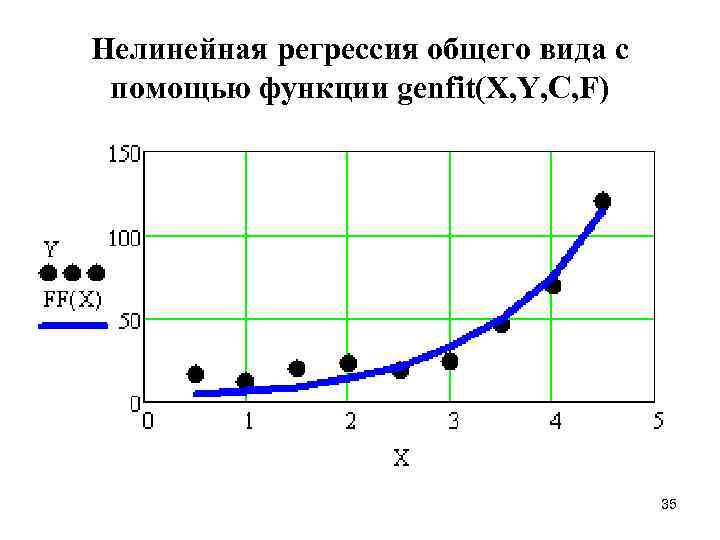
Нелинейная регрессия общего вида с помощью функции genfit(X, Y, C, F) 35
Журов_Лекция_12_2012.ppt