Обозначается: Определитель – это число, характеризующее квадратную






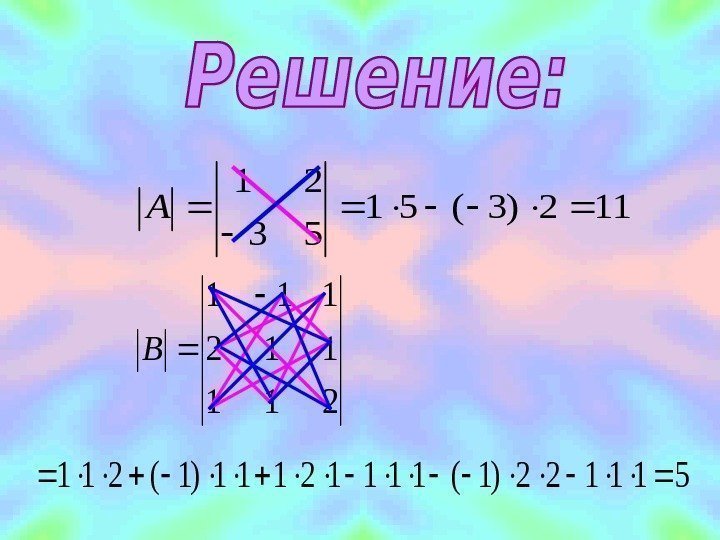







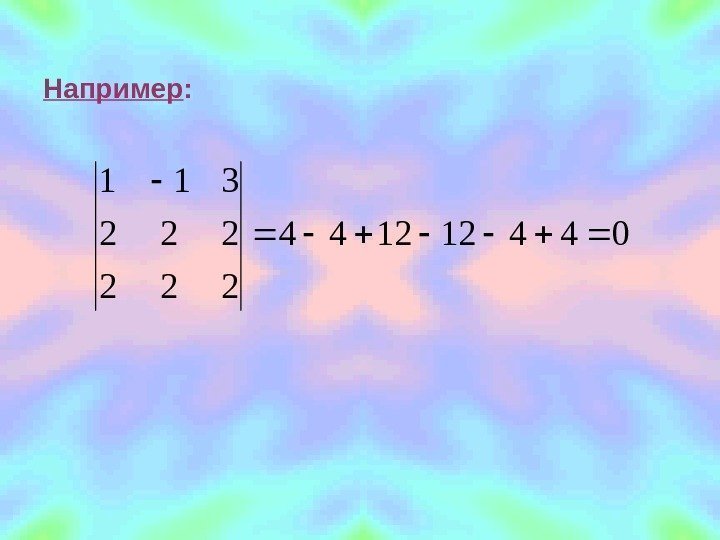








1.2.ppt
- Размер: 323.0 Кб
- Автор: Шамиль Имамов
- Количество слайдов: 24
Описание презентации Обозначается: Определитель – это число, характеризующее квадратную по слайдам
 Обозначается: Определитель – это число, характеризующее квадратную матрицу. A Adet
Обозначается: Определитель – это число, характеризующее квадратную матрицу. A Adet
 Определителем первого порядка матрицы)( 11 a. A называется число 11 a То есть: 1111 aa.
Определителем первого порядка матрицы)( 11 a. A называется число 11 a То есть: 1111 aa.
 Определителем второго порядка называется число, которое определяется по правилу: 21122211 2221 1211 aaaa aa aa
Определителем второго порядка называется число, которое определяется по правилу: 21122211 2221 1211 aaaa aa aa
 Определителем третьего порядка называется число, которое определяется по правилу: 322311332112312213 322113312312332211 333231 232221 131211 aaaaaaaaa aaa aaa
Определителем третьего порядка называется число, которое определяется по правилу: 322311332112312213 322113312312332211 333231 232221 131211 aaaaaaaaa aaa aaa
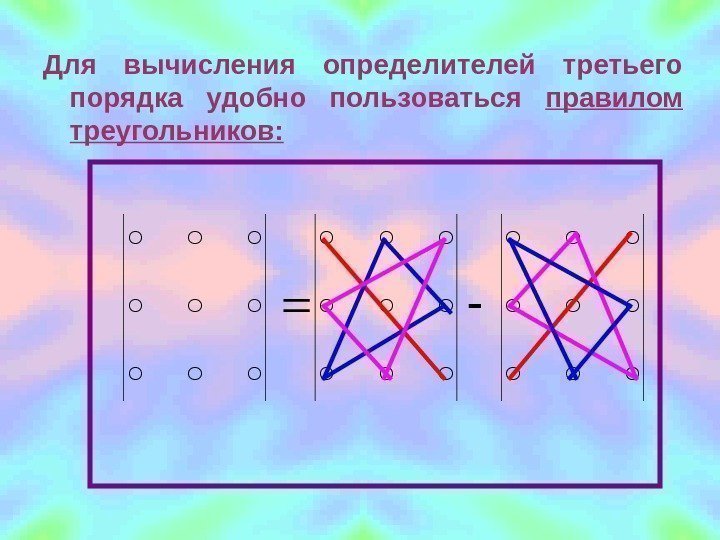
 Для вычисления определителей третьего порядка удобно пользоваться правилом треугольников:
Для вычисления определителей третьего порядка удобно пользоваться правилом треугольников:
 211 112 111 53 21 BAВычислить определители матриц :
211 112 111 53 21 BAВычислить определители матриц :
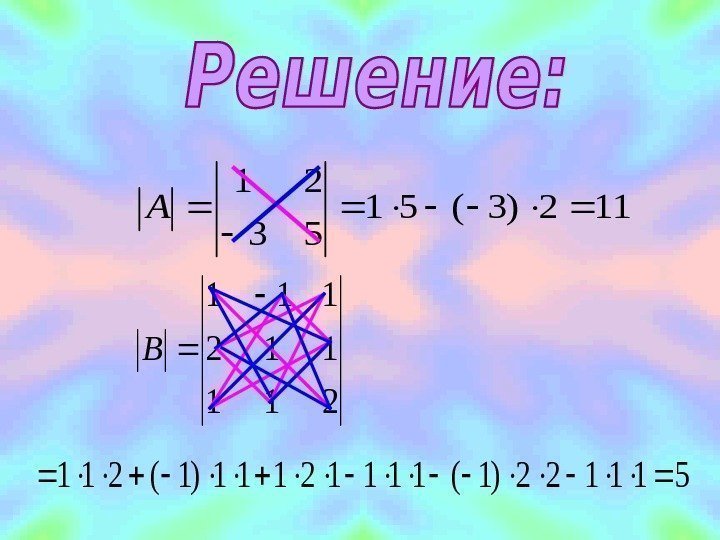 112)3(51 53 21 A 211 112 111 B 511122)1(11112111)1(
112)3(51 53 21 A 211 112 111 B 511122)1(11112111)1(
 Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Минор элемента определителя ija обозначается как ij M
Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Минор элемента определителя ija обозначается как ij M
 Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на (-1 ) S , где S – сумма номеров строки и столбца, на пересечении которых стоит данный элемент. ij S ij MA )1( ji. S
Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на (-1 ) S , где S – сумма номеров строки и столбца, на пересечении которых стоит данный элемент. ij S ij MA )1( ji. S
 В частности, минор элемента 11 a 333231 232221 131211 aaa aaa 3332 2322 11 aa aa Mопределителя третьего порядка найдется по правилу: Его алгебраическое дополнение: 111111 11 )1( MM
В частности, минор элемента 11 a 333231 232221 131211 aaa aaa 3332 2322 11 aa aa Mопределителя третьего порядка найдется по правилу: Его алгебраическое дополнение: 111111 11 )1( MM
 1 Определитель транспонированной матрицы равен определителю исходной матрицы. T
1 Определитель транспонированной матрицы равен определителю исходной матрицы. T
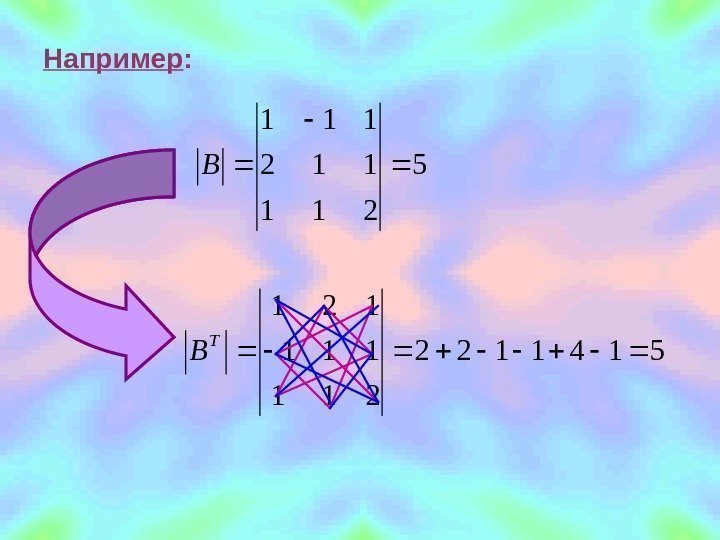
 Например : 5 211 112 111 B 5141122 211 121 T
Например : 5 211 112 111 B 5141122 211 121 T
 2 Перестановка двух строк или столбцов определителя эквивалентна умножению его на (-1).
2 Перестановка двух строк или столбцов определителя эквивалентна умножению его на (-1).
 Например : 5 211 112 111 B 5221114 211 112 Меняем местами первую и вторую строки:
Например : 5 211 112 111 B 5221114 211 112 Меняем местами первую и вторую строки:
 3 Если определитель имеет две одинаковые строки или столбца, то он равен нулю.
3 Если определитель имеет две одинаковые строки или столбца, то он равен нулю.
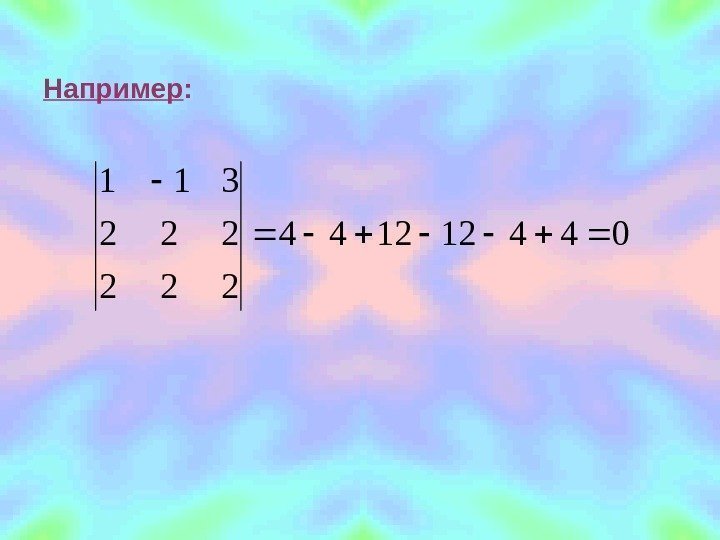 Например :
Например :
 4 Общий множитель строки или столбца можно выносить за знак определителя.
4 Общий множитель строки или столбца можно выносить за знак определителя.
 Например : Выносим из второй строки множитель 2: 4242224 211 222 111 422)121112(
Например : Выносим из второй строки множитель 2: 4242224 211 222 111 422)121112(
 5 Определитель не изменится, если к элементам одной строки или столбца прибавить соответственные элементы другой строки или столбца, умноженные на одно и то же число.
5 Определитель не изменится, если к элементам одной строки или столбца прибавить соответственные элементы другой строки или столбца, умноженные на одно и то же число.
 Например : 5 211 112 111 B Первую строку умножаем на 2 и складываем со второй:
Например : 5 211 112 111 B Первую строку умножаем на 2 и складываем со второй:
 6 Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения: n k ikikininiiii. Aa. Aa. A 1 2211. . .
6 Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения: n k ikikininiiii. Aa. Aa. A 1 2211. . .
 Вычислить определитель :
Вычислить определитель :
 Раскладываем определитель по третьей строке: 3332343332310110 1432 0110 1321 4321 AAAAAA = Находим алгебраические дополнения:
Раскладываем определитель по третьей строке: 3332343332310110 1432 0110 1321 4321 AAAAAA = Находим алгебраические дополнения:
 332161242 132 121 421 )1(3333 33 MA Подставляем полученный результат: 6)43241663( 142 131 431 )1( 3223 32 MA 3)3(6 =
332161242 132 121 421 )1(3333 33 MA Подставляем полученный результат: 6)43241663( 142 131 431 )1( 3223 32 MA 3)3(6 =

