Обоснование задачи


Обоснование задачи сопоставления и сравнения Очень часто перед исследователем в психологии стоит задача выявления различий между двумя, тремя и более выборками испытуемых. Это может быть, например, задача определения психологических особенностей юных правонарушителей по сравнению с законопослушными сверстниками или различий между работниками государственных предприятий и частных фирм, между людьми разной национальности или разной культуры и, наконец, между людьми разного возраста в методе "поперечных срезов". В предыдущих лекциях нам стало известно, что по наблюдениям случайной выборки на основе свойств распределения признака можно оценить некоторые неизвестные параметры интересующего исследователя случайного признака для всей генеральной совокупности. Однако важными вопросами для нас оказываются следующие: Ø Насколько значимы полученные на уровне сравнения средних значений и мер изменчивости различия? Можно ли перенести сделанные выводы на всю генеральную совокупность? Ø Если мы располагаем некоторыми предварительными (априорными) догадками или предположениями относительно численной величины этих параметров или о законе распределения вероятностей признака, как в таком случае можно проверить гипотезу о том, что наша догадка действительно верна? 2

Суходольский Геннадий Владимирович Вся профессиональная жизнь Г. В. Суходольского прошла в (1934 -2008) стенах Ленинградского—Санкт Петербургского университета: со времени окончания отделения психологии философского факультета ЛГУ в 1962 г. и до последних дней жизни. Им пройден путь от лаборанта первой в СССР лаборатории индустриальной психологии, где он работал под непосредственным руководством основателя инженерной психологии академика Б. Ф. Ломова, до заведующего кафедрой эргономики и инженерной психологии. Профессор Г. В. Суходольский стал одним из ведущих специалистов России в области психологии труда, инженерной психологии и математической психологии, имел огромный опыт научной, прикладной и педагогической деятельности. Написанные им монографии и учебники позволяют по праву назвать его одним из основателей ленинградской, затем петербургской школы инженерной психологии. Участвовал в организации и проведении в период с 1964 по 1990 г. всех всесоюзных конференций по инженерной психологии. Г. В. Суходольский многие годы занимался проблемами математической психологии. К числу разработанных им оригинальных методов относятся: метод многомерных помеченных стохастических матриц для пор третирования сложных объектов; метод визуализации конечномерных объектов в виде профиля в параллельных координатах; метод использования мультимножеств, операции обобщения, смешанного умножения и деления мультимножеств и матриц данных; новый метод оценки значимости коэффициентов корреляции с помощью F критерия Снедекора—Фишера и значимости сходства — различия корреляционных матриц по G критерию Кохрена; метод нормализации распределений через 3 интегральную функцию.

Особенности формулировки гипотез (по Г. В. Суходольскому) Решение любой статистической задачи начинается с постановки гипотез. Формулирование гипотез систематизирует предположения исследователя и представляет их в четком и лаконичном виде. Благодаря гипотезам исследователь не теряет путеводной нити в процессе расчетов и ему легко понять после их окончания, что собственно он обнаружил. Слово " гипотеза " в переводе с греческого означает основание, или предположение, которое предваряет тезис - определенное утверждение либо положение в рассуждении, высказываемое оратором. Не всякое предположение считается научным. К числу научных гипотез относят лишь такие, которые хотя бы в принципе, в будущем могут быть проверены. Эмпирическая проверка гипотезы называется верификацией. По научной принадлежности , т. е. по имени той науки, в которой гипотезы высказываются, формулируются и проверяются, можно различать физические, математические, психологические и другие гипотезы. Они различаются объектами , в отношении которых выдвигаются, языковыми средствами , с помощью которых формулируются, и способами верификации , используемыми в конкретной науке. Например , математические гипотезы выдвигаются по поводу математических объектов, формулируются на математическом языке и проверяются математическими доказательствами или расчетом. Точно так же психологические гипотезы выдвигаются в отношении психологических объектов, формулируются на языке психологии и верифицируются результатами наблюдения и психологического эксперимента. 4

Примеры гипотез (по Г. В. Суходольскому) Особый интерес для психологии представляют статистические гипотезы, которые выдвигаются по поводу массовых, случайных явлений, формулируются на теоретико вероятностном языке и проверяются математико статистическими методиками. В психологии объекты изучения обладают всеми формальными свойствами случайных явлений случайных событий, случайных величин и функций. Человек или социальная общность, психические свойства которых изучаются психологами, формируется, живет и функционирует в стохастической среде, влияние которой тоже подчиняется стохастическим закономерностям. Все это приводит к тому, что психологические гипотезы оказываются в то же время гипотезами статистическими. Можно сказать, что психологические гипотезы скрывают под собой статистическую сущность, которая должна быть выявлена и корректно использована для статистической проверки психологических гипотез. Речь, следовательно, идет о прямой и обратной, психолого статистической, интерпретации: психологическую гипотезу нужно сначала адекватным образом переформулировать в гипотезу статистическую, имея в виду подходящий способ статистической проверки; затем эту проверку надо осуществить, а результаты обратно переформулировать в статистически 5 обоснованный психологический вывод.

Пример № 1 (по Г. В. Суходольскому) Предполагается, что несколько признаков поведения человека в определенной ситуации образуют устойчивый синдром. Но синдром из качественных признаков интерпретируется в теоретико вероятностном смысле как сложное случайное событие, вероятность которого должна быть значительно больше, чем вероятность составляющих его простых событий; а синдром из количественных признаков интерпретируется как матрица высокозначимых корреляций между симптомами. Поэтому для проверки гипотезу о синдроме нужно переформулировать в статистическую гипотезу о значимости различий между совместной и частными вероятностями симптомов либо о значимости корреляций между симптомами. Значимость корреляций практически проверяется их сравнением с критическим, для определенного числа наблюдений, значением коэффициента корреляции. Статистические гипотезы вообще принимаются или отклоняются в зависимости от числа наблюдений, причем одна и та же гипотеза может быть отклонена при малом числе наблюдений, но принята, если наблюдений станет достаточно много. Только статистически проверив, значимы или не значимы корреляции симптомов или различия вероятностей синдрома и образующих его симптомов, можно затем психологически 6 интерпретировать эти результаты в терминах психодиагностики.

Пример № 2 (по Г. В. Суходольскому) В психологии труда существенное значение имеют оценки времени реакции людей водительских профессий: от времени реакции во многом зависит безопасность участников движения транспорта. Известно, что время реакции увеличивается при утомлении водителя, и требуется проверить, увеличивается ли время реакции, скажем, шофера при длительном вождении автомобиля. Для адекватной статистической переформулировки этой гипотезы следует вспомнить, что время реакции человека является случайной величиной, которая полностью характеризуется распределением вероятностей своих значений и теоретически аппроксимируется нормальным или гамма распределением. У этих распределений есть два формообразующих параметра математическое ожидание и дисперсия. Следовательно, объектами наблюдения должны быть либо распределения, либо их параметры средние времени реакции и дисперсии этого времени. Далее нужно вспомнить, что зависимость определяется как изменение наблюдений при изменении условий. Следовательно, в гипотезе о зависимости времени реакции должна идти речь об условных распределениях, либо их параметрах условных средних и дисперсиях. Для того чтобы установить сам факт влияния длительности вождения на время реакции, достаточно сравнить два условных распределения до и после вождения, либо конъюнкцию условных средних и дисперсий до вождения сравнить с конъюнкцией этих параметров после вождения. Но чтобы выявить саму зависимость и представить ее в виде прогнозной модели, необходимо в ходе наблюдения получить несколько условных распределений времени реакции, при условии увеличивающихся длительностей вождения, либо получить соответствующие векторы условных средних и условных дисперсий. При этом, конечно, усложняются сами гипотезы и способы их проверки, а экспериментальное исследование должно быть спланировано и проведено по плану. 7

Определение Под статистической гипотезой обычно понимают формальное предположение о том, что сходство (или различие) некоторых характеристик случайно или, наоборот, неслучайно. Статистической гипотезой (в дальнейшем для краткости будем говорить просто «гипотезой» ) называется любое предположение о модели закона распределения вероятностей исследуемого случайного признака, о числовых значениях параметров этого закона распределения, о модели зависимости между анализируемыми признаками. Например, статистическими гипотезами будут: а) гипотеза о том, что исследуемая случайная величина подчиняется нормальному закону распределения вероятностей, б) гипотеза о том, что математическое ожидание исследуемой случайной величины равно заданному числу, в) гипотеза о том, что дисперсии двух исследуемых случайных величин равны между собой, г) гипотеза о том, что две исследуемые случайные величины являются корреляционно зависимыми. Гипотеза «на Луне имеется вода» не является статистической гипотезой, поскольку в ней не идет речь о случайном признаке. 8

Виды гипотез: простые и сложные В науке различают простые и сложные, отдельные, альтернативные и множественные гипотезы. Ø Гипотезу, которая однозначно определяет все параметры распределения, называют простой. Ø Гипотезу, состоящую из конечного или бесконечного числа простых гипотез, называют сложной. Сложные гипотезы строятся из простых с помощью логических композиций. В качестве средств композиции обычно принимаются нормальные конъюнктивно дизъюнктивные формы типа: А и В, или А и не В, или не А и В, или не А и не В. Например: гипотеза о том, что исследуемый нормально распределенный признак имеет параметр а = 2 и параметр σ 2 = 9, является простой, гипотеза о том, что исследуемый нормально распределенный признак имеет параметр а >2 и параметр σ 2 =9, является сложной, так как она состоит из бесконечного числа простых гипотез о числовом значении параметра а > 2. 9

Виды гипотез: нулевая и альтернативная Отдельная гипотеза представляет собой то предположение, которое интересует исследователя. Но, как и случайные события, гипотезы образуют множества. Простейшее из них множество альтернативных гипотез: Н 0 так называемая нулевая или «основная» гипотеза, Н 1 противоположная ей, альтернативная, или «экспериментальная» , или «конкурирующая» гипотеза. Альтернативные гипотезы по смыслу тождественны противоположным событиям: если принимается одна, то отклоняется другая. Нулевая гипотеза (Н 0 ) – гипотеза о сходстве, т. е. об отсутствии различий, то, что мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий. Она называется нулевой, т. к. содержит число 0, то есть: Х 1 – Х 2 = 0, где Х 1 и Х 2 – сопоставляемые значения признаков. Альтернативная гипотеза (Н 1 ) – гипотеза о различии, то, что мы хотим доказать, поэтому ее так же называют экспериментальной гипотезой. Это гипотеза о наличии значимых различий между показателями или о достоверности связи между ними. 10

Пример гипотез: нулевая и альтернативная Например, необходимо выяснить, одинаков ли умственный уровень у учеников школ № 1 и № 2. Перед началом проведения исследования необходимо сформулировать соответствующие гипотезы. В нашем случае нулевая и альтернативная гипотезы будут выглядеть следующим образом: Н 0: уровни умственного развития учеников школ № 1 и № 2 не отличаются друг от друга. Н 1: уровни умственного уровня учеников школ № 1 и № 2 значимо различны. Следует иметь в виду, что речь идет не об арифметических (то есть числовых) различиях, а о статистически значимых различиях. При этом возникает вопрос о том, какие различия можно считать статистически значимыми. 11
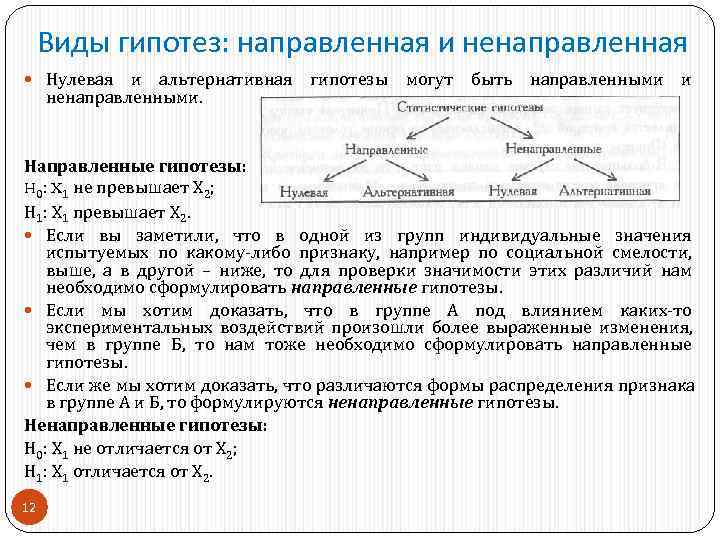
Виды гипотез: направленная и ненаправленная Нулевая и альтернативная гипотезы могут быть направленными и ненаправленными. Направленные гипотезы: H 0: X 1 не превышает Х 2; H 1: X 1 превышает Х 2. Если вы заметили, что в одной из групп индивидуальные значения испытуемых по какому либо признаку, например по социальной смелости, выше, а в другой – ниже, то для проверки значимости этих различий нам необходимо сформулировать направленные гипотезы. Если мы хотим доказать, что в группе А под влиянием каких то экспериментальных воздействий произошли более выраженные изменения, чем в группе Б, то нам тоже необходимо сформулировать направленные гипотезы. Если же мы хотим доказать, что различаются формы распределения признака в группе А и Б, то формулируются ненаправленные гипотезы. Ненаправленные гипотезы: H 0: X 1 не отличается от Х 2; Н 1: Х 1 отличается от Х 2. 12

Пример гипотез: направленная и ненаправленная Приведенный в предыдущем примере (слайд 11)набор гипотез — это ненаправленные гипотезы. В Н 1 указывается, что показатели различны, однако не говорится о том, какой показатель больше другого (умственный уровень различен, но нет гипотезы относительно того, в какой школе ученики умнее, а в какой наоборот). Направленные гипотезы не только говорят о наличии либо отсутствии различий, но и указывают направление различий. Таким образом, направленных гипотез можно выдвинуть в два раза больше (две нулевые и две альтернативные), чем ненаправленных. Применительно к нашему примеру они будут выглядеть следующим образом: Н 0 : уровень умственного развития учеников школы № 1 не превосходит 1 показатель умственного развития учеников школы № 2. Н 1 : умственный уровень учеников школы № 1 превосходит умственный 1 уровень учеников школы № 2. Н 0 : уровень умственного развития учеников школы №. 2 не превосходит 2 показатель умственного развития учеников школы № 1. Н 1 : умственный уровень учеников школы № 2 превосходит умственный 2 уровень учеников школы № 1. 13

Ошибки первого и второго рода Статистическая проверка гипотез, основанная на экспериментальных выборочных данных, всегда вероятностна, т. е. связана с риском (вероятностью) принятия ложного решения. При этом возможны ошибки двух родов. Ошибка первого рода (вероятность ошибки первого рода – р или α) произойдет, когда будет принято решение отклонить гипотезу Н 0 , хотя в действительности она была верной. Г. Суходольский: Ошибка первого рода имеет разные содержательные интерпретации. Так, в теории наблюдателя эту ошибку называют пропуском цели, в маркетинге риском заказчика: он пропускает некондиционный товар, а в психологии ее можно интерпретировать как проявление невнимательности человека Ошибка второго рода (вероятность ошибки второго рода – β ) произойдет, когда будет принято решение не отклонять гипотезу Н 0, хотя в действительности она будет неверной Г. Суходольский: Эта ошибка тоже имеет интерпретации ложная тревога у наблюдателя, риск поставщика в маркетинге: у него ошибочно отказываются брать кондиционный товар, а в психологии за ошибками второго рода скрывается личностная тревожность человека. Верным решением при ложности гипотезы должно быть ее отклонение. Вероятность ошибки 1 го рода называется также уровнем значимости (критерия и др. ). Вероятность ошибки 2 го рода называют также мощностью критерия. 14

Вероятность ошибки Проверяемая гипотеза объективно может быть истинной либо ложной. Истинность гипотезы означает, что предполагаемые свойства объекта существуют в действительности, а ее ложность означает реальное отсутствие гипотетических свойств. Субъект, который проверяет гипотезу, заранее не может знать о том, истинная она или ложная. Он пытается установить это в ходе проверки и в результате принимает гипотезу за истинную либо отклоняет как ложную. При этом он, естественно, делает ошибки, принимая ложную гипотезу за истинную или отклоняя истинную гипотезу как ложную. Эти ошибки имеют важное значение для математической статистики и математической психологии, потому что они характеризуют качество прогноза и определенные психологические свойства человека или группы экспертов, исполняющих функции лица, принимающего решения. 15

Взаимодействие ошибок первого и второго рода При фиксированном объеме выборочных данных уровень значимости р заранее задается. Наиболее распространенными на практике значениями р являются 0, 01; 0, 05; 0, 1, что соответственно указывает на вероятность получения достоверного вывода (1 р), равную 0, 99; 0, 95; 0, 90. Например, задание уровня значимости р = 0, 05 означает, что при многократном использовании данного статистического критерия в пяти случаях из ста будет ошибочно отвергаться гипотеза Н 0. Ошибки 1 го и 2 го родов зависят друг от друга. Если объем выборки фиксирован, то чем меньше будет р, тем больше будет β, и наоборот. Другими словами, чем меньше а, тем меньше мощ ность 1 ( - β), и наоборот. При слишком малом объеме выборки п при заданном уровне значимости р мощность (1 β) может оказаться слишком маленькой. В таком случае либо увеличивают объем выборки, либо увеличивают уровень значимости р, что позволит увеличить мощность. 16

Возникает вопрос: какая из этих ошибок более важна для исследователя, какую из них важнее не допустить? Ответ на этот вопрос неоднозначен и зависит от ряда обстоятельств: 1. от целей, которые преследуются в эксперименте; 2. от предмета изучения и характера задачи исследования; 3. от схемы построения исследования. Например, присяжные, определяя виновность или невинов ность одсудимого, п должны решить, что более значимо: признать невиновного виновным или наоборот. Установка на гуманность диктует правило: пусть будут оправданы десять преступников, чем пострадает один невиновный. Репрессивная же установка предполагает другое правило: пусть пострадают десять невиновных, лишь бы один виновный не ушел от наказания. Ошибка первого рода существенна в конфирматорном (уточняющем) эксперименте, а также тогда, когда непринятие верной гипотезы об отсутствии различий имеет практическую значимость: так, принятие ложной гипотезы об интеллектуальных различиях представителей разных социальных страт или этнических групп может иметь серьезные социально политические последствия. Ошибка второго рода существенна в эксплораторном (разведочном) эксперименте. Отклонение гипотезы о различиях на на чальной тадии может с 17 надолго дезориентировать исследователя в отношении изучаемых закономерностей.

Поэтому уровень статистической достоверности проведении эксплораторного эксперимента стремятся понизить, применяя два способа: 1. проведение эксплораторного эксперимента на малых выбор ках, т. е. уменьшение количества наблюдений; 2. задание невысокого уровня значимости (р=0, 1 или 0, 05). Субъективно исследователю приятнее получить подтверждение своих гипотез, чем их опровержение, поэтому у начинающих психологов вероятность ошибок первого рода значительно выше, чем ошибок второго рода. Следовательно, важно стремиться обезопасить себя, в первую очередь, от ошибок первого рода. Стратегия экспериментального исследования в любой области психологической науки может быть представлена следующей схемой, включающей ряд возможных переходов: 1. от эксплораторного эксперимента к конфирматорному; 2. от низких уровней достоверности к высоким; 3. от исследований на малых выборках к большим. 18

Уровень статистической значимости Каким же образом можно судить о принятом решении: насколько оно верно и с какой вероятностью? Вероятность ошибки базируется на понятии уровня значимости. Уровень статистической значимости ( Significant level ), или р уровень значимости ( p level ), – основной результат проверки статистической гипотезы. Это вероятность того, что мы сочли различия существенными, а они на самом деле случайны (вероятность отклонения нулевой гипотезы, в то время как она верна – ошибка первого рода). Чем меньше эта вероятность, тем надёжнее результат. Полезно знать, что влияет на уровень значимости: уровень значимости выше (значение р уровня меньше), если: 1. величина связи (или различия) больше; 2. изменчивость признака (признаков) меньше; 3. объём выборки (выборок) больше; При этом, чем больше гипотез проверяется, тем выше шанс получить случайный результат. Возможность проверить результаты – провести параллельное исследование на идентичной выборке. 19

Оценка уровня и степени свободы Исторически сложилось так, что в прикладных науках, использующих статистику, и в частности в психологии, низшим считается уровень статистической значимости, равный 0, 05, достаточным – уровень, равный 0, 01, и высшим – 0, 001. То есть, например, если уровень значимости равен 0, 05, это значит, что в выборе из 100 элементов (случаев, испытуемых) допускается 5 ошибок, другими словами, это 5 процентная вероятность того, что мы ошиблись. Аналогично рассчитываются уровни 0, 01 и 0, 001. В таблицах критических значений приводятся или показатели объема выборки, или показатели степеней свободы. Степень свободы (обозначается как df или v ) — это величина, зависимая от объема выборки. Если мы не определили степень свободы, то мы не сможем пользоваться статистическими таблицами. Число степеней свободы — это число данных из выборки, значения которых могут быть случайными. В любом случае при объеме выборки п мы будем иметь число степеней свободы равным п — 1. Если у нас имеются две независимые выборки, то число степеней свободы для первой из них составляет п 1 1, а для второй — п 2 1. Таким образом, число степеней свободы для этих независимых выборок будет составлять (п 1 + п 2) - 2. В случае зависимых выборок число степеней свободы равно п 1. 20
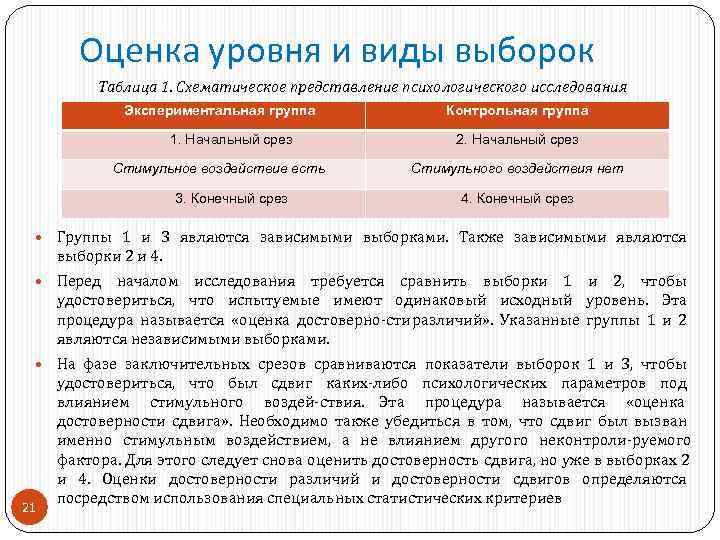
Оценка уровня и виды выборок Таблица 1. Схематическое представление психологического исследования Экспериментальная группа Контрольная группа 1. Начальный срез 2. Начальный срез Стимульное воздействие есть Стимульного воздействия нет 3. Конечный срез 4. Конечный срез Группы 1 и 3 являются зависимыми выборками. Также зависимыми являются выборки 2 и 4. Перед началом исследования требуется сравнить выборки 1 и 2, чтобы удостовериться, что испытуемые имеют одинаковый исходный уровень. Эта процедура называется «оценка достоверно сти различий» . Указанные группы 1 и 2 являются независимыми выборками. На фазе заключительных срезов сравниваются показатели выборок 1 и 3, чтобы удостовериться, что был сдвиг каких либо психологических параметров под влиянием стимульного воздей ствия. Эта процедура называется «оценка достоверности сдвига» . Необходимо также убедиться в том, что сдвиг был вызван именно стимульным воздействием, а не влиянием другого неконтроли руемого фактора. Для этого следует снова оценить достоверность сдвига, но уже в выборках 2 и 4. Оценки достоверности различий и достоверности сдвигов определяются посредством использования специальных статистических критериев 21

Для каждого статистического критерия задается некоторая функция S от результатов наблюдения S = S ( x v х 2 , . . . , х п ), которая называетс статистикой критерия. Статистика критерия может обозначаться и по другому. Эта функция S, как и всякая функция от результатов наблюдения, сама является случайной величиной. В предположе нии праведливости гипотезы Н 0 с статистика критерия S подчинена хорошо изученному и затабулированному закону распределения. Множество всех значений статистики S разбивается при заданном уровне значимости р на два непересекающихся подмножества. 1. Одно подмножество содержит все те значения S , при которых гипотеза Н 0 принимается, и называется областью принятия гипотезы Н 0. 2. Другое подмножество содержит все те значения S, при которых гипотеза Н 0 отвергается, и называется критической областью. Область принятия гипотезы Я и критическая область являются 0 интервалами, а точки, которые разделяют эти интервалы, называют критическими значениями статистики S. Различают три типа критических областей: левостороннюю критическую область, правостороннюю критическую область и двустороннюю критическую область. В зависимости от типа критической области статистические критерии подразделяют на левосторонние, правосторонние и двусторонние. 22
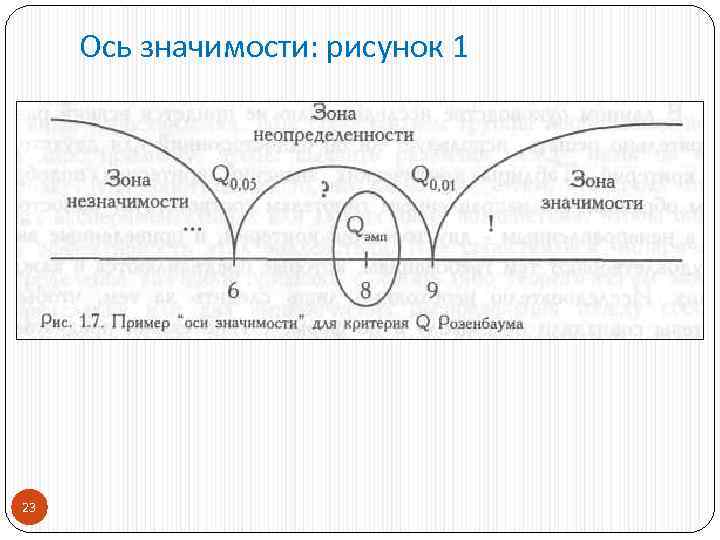
Ось значимости: рисунок 1 23

Ось значимости: рисунок 2 Замечания К сожалению, специалисты, применяющие статистические методы, часто вместо того, чтобы отметить, что уровень значимости их данных лежит между 2, 5 и 5%, сообщают лишь о том, что он менее 5%. Для этого используется выражение «данные значимы на уровне 5%» (аналогично и для других уровней). Подчеркнем, что в такой формулировке оно означает следующее: уровень значимости данных не более чем 0, 05. 24

Таблицы критических значений Для определения по статистическим таблицам критических значений необходимо знать: v определение уровня значимости, v число степеней свободы (degrees of freedom, сокращенно df) для данной выборки. Как правило, оно равно N 1, где N – количество измерений, исключения оговариваются в алгоритме расчёта критерия. v В таблицах критических значений не всегда указано число степеней свободы, соответствующее конкретному исследованию. Предпочтение необходимо отдавать меньшему значению степеней свободы. Число, превышающее число степеней свободы, полученное в исследовании, в таблице выбирать нельзя. 25

Вопросы для самостоятельной работы: Допустим, требуется сравнить уровень интеллекта мужчин и женщин. Как будут выглядеть нулевая и альтернативная гипотезы данного исследования? Привести собственные примеры зависимой и независимой выборок. Чему равна степень свободы для двух зависимых выборок объемом п = 6? Чему равна степень свободы для двух независимых выборок при п 1 = 10 и п 2 = 12? 26
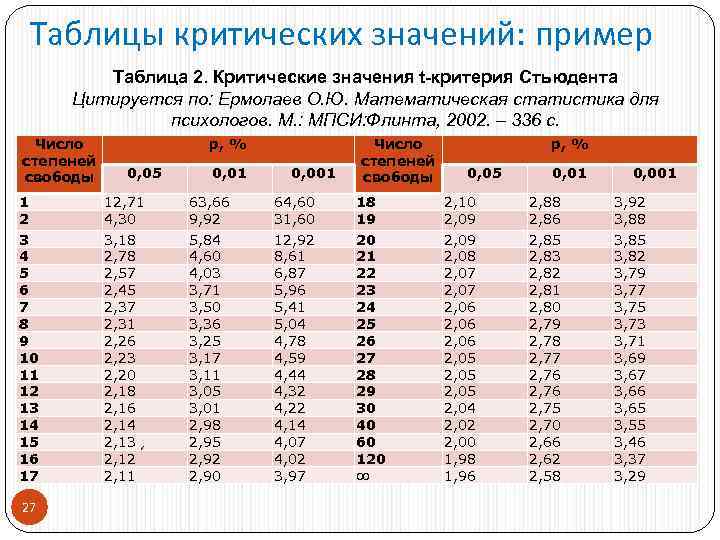
Таблицы критических значений: пример Таблица 2. Критические значения t-критерия Стьюдента Цитируется по: Ермолаев О. Ю. Математическая статистика для психологов. М. : МПСИ: Флинта, 2002. – 336 с. Число р, % степеней степеней свободы 0, 05 0, 01 0, 001 свободы 0, 05 0, 01 0, 001 1 12, 71 63, 66 64, 60 18 2, 10 2, 88 3, 92 2 4, 30 9, 92 31, 60 19 2, 09 2, 86 3, 88 3 3, 18 5, 84 12, 92 20 2, 09 2, 85 3, 85 4 2, 78 4, 60 8, 61 21 2, 08 2, 83 3, 82 5 2, 57 4, 03 6, 87 22 2, 07 2, 82 3, 79 6 2, 45 3, 71 5, 96 23 2, 07 2, 81 3, 77 7 2, 37 3, 50 5, 41 24 2, 06 2, 80 3, 75 8 2, 31 3, 36 5, 04 25 2, 06 2, 79 3, 73 9 2, 26 3, 25 4, 78 26 2, 06 2, 78 3, 71 10 2, 23 3, 17 4, 59 27 2, 05 2, 77 3, 69 11 2, 20 3, 11 4, 44 28 2, 05 2, 76 3, 67 12 2, 18 3, 05 4, 32 29 2, 05 2, 76 3, 66 13 2, 16 3, 01 4, 22 30 2, 04 2, 75 3, 65 14 2, 14 2, 98 4, 14 40 2, 02 2, 70 3, 55 15 2, 13 , 2, 95 4, 07 60 2, 00 2, 66 3, 46 16 2, 12 2, 92 4, 02 120 1, 98 2, 62 3, 37 17 2, 11 2, 90 3, 97 ∞ 1, 96 2, 58 3, 29 27

Правила принятия гипотезы В общем виде правила отклонения Н 0 и принятия Н 1 (Рунион Р. , 1982): 1. Если эмпирическое значение критерия равняется критическому значению, соответствующему уровню значимости 0, 05, или превышает его, то Н 0 отклоняется, но мы еще не можем определенно принять Н 1. 2. Если эмпирическое значение критерия равняется критическому значению, соответствующему уровню значимости 0, 01, или превышает его, то Н 0 отклоняется и принимается Н 1. 3. Существуют исключения: критерий знаков G , критерий T Вилкоксона и критерий U Манна – Уитни. Для них установлены обратные соотношения. Практически принимается p<0, 05. 4. Существуют таблицы критических значений для каждого критерия. 28

Определение статистического критерия Статистический критерий ( Statistical Test ) – решающее правило, обеспечивающее принятие истиной и отклонение ложной гипотезы с высокой вероятностью (Суходольский Г. В. , 1972). В качестве основы для применения критериев используют теоретические распределения для условия, когда верна гипотеза. Критерий подразумевает формулу, применяя которую исследователь получает эмпирическое значение критерия. Таким образом, статистический критерий – это одновременно и метод расчета определенного числа, и само это число. 29

Мощность критерия Главной характеристикой критерия является его мощность. Это способность критерия выявлять различия, если они есть. Иными словами, это его способность отклонить нулевую гипотезу, если она неверна. Таким образом, мощность критерия работает с ошибкой второго рода. Т. е. мощность критерия характеризует его способность избегать ошибки второго рода. 30

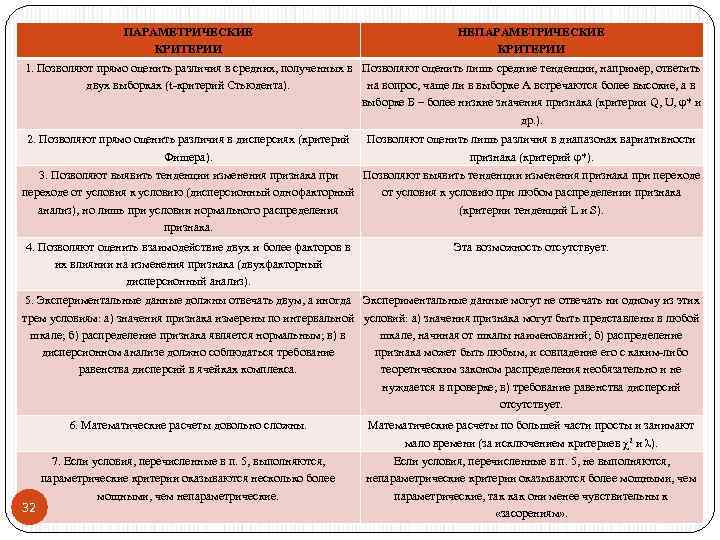
Виды статистических критериев Параметрические критерии основаны на конкретном типе распределения генеральной совокупности (как правило, нормальном) и используют параметры этой совокупности (средние, дисперсии и проч. ). Непараметрические критерии не базируются на предположении о типе распределении признака и не используют параметры этой совокупности, основываются на оперировании частотами или рангами. Параметрические критерии считаются более мощными ( при условии нормальности распределения ). Поэтому им следует отдавать предпочтение, если распределение признака близко к нормальному. Однако большинство данных, получаемых в ходе психологических исследований, не распределены нормально. В этом случае оказываются более мощными непараметрические критерии. И те, и другие критерии имеют свои преимущества и недостатки. На основании нескольких руководств можно составить таблицу, позволяющую оценить возможности и ограничения тех и других : 31
ПАРАМЕТРИЧЕСКИЕ НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 1. Позволяют прямо оценить различия в средних, полученных в Позволяют оценить лишь средние тенденции, например, ответить двух выборках (t-критерий Стьюдента). на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б – более низкие значения признака (критерии Q, U, φ* и др. ). 2. Позволяют прямо оценить различия в дисперсиях (критерий Позволяют оценить лишь различия в диапазонах вариативности Фишера). признака (критерий φ*). 3. Позволяют выявить тенденции изменения признака при переходе от условия к условию (дисперсионный однофакторный от условия к условию при любом распределении признака анализ), но лишь при условии нормального распределения (критерии тенденций L и S). признака. 4. Позволяют оценить взаимодействие двух и более факторов в Эта возможность отсутствует. их влиянии на изменения признака (двухфакторный дисперсионный анализ). 5. Экспериментальные данные должны отвечать двум, а иногда Экспериментальные данные могут не отвечать ни одному из этих трем условиям: а) значения признака измерены по интервальной условий: а) значения признака могут быть представлены в любой шкале; б) распределение признака является нормальным; в) в шкале, начиная от шкалы наименований; б) распределение дисперсионном анализе должно соблюдаться требование признака может быть любым, и совпадение его с каким-либо равенства дисперсий в ячейках комплекса. теоретическим законом распределения необязательно и не нуждается в проверке; в) требование равенства дисперсий отсутствует. 6. Математические расчеты довольно сложны. Математические расчеты по большей части просты и занимают мало времени (за исключением критериев χ 2 и λ). 7. Если условия, перечисленные в п. 5, выполняются, Если условия, перечисленные в п. 5, не выполняются, параметрические критерии оказываются несколько более непараметрические критерии оказываются более мощными, чем непараметрические. параметрические, так как они менее чувствительны к 32 «засорениям» .
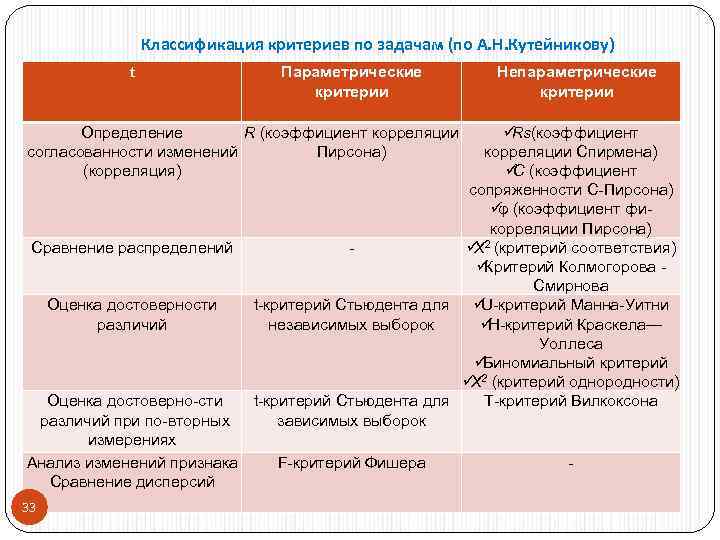
Классификация критериев по задачам (по А. Н. Кутейникову) t Параметрические Непараметрические критерии Определение R (коэффициент корреляции üRs(коэффициент согласованности изменений Пирсона) корреляции Спирмена) (корреляция) ü (коэффициент С сопряженности С Пирсона) ü (коэффициент фи φ корреляции Пирсона) Сравнение распределений - üΧ 2 (критерий соответствия) üКритерий Колмогорова Смирнова Оценка достоверности t критерий Стьюдента для ü U критерий Манна Уитни различий независимых выборок ü Н критерий Краскела— Уоллеса ü Биномиальный критерий ü 2 (критерий однородности) X Оценка достоверно сти t критерий Стьюдента для T критерий Вилкоксона различий при по вторных зависимых выборок измерениях Анализ изменений признака F критерий Фишера - Сравнение дисперсий 33

Сравнительный анализ измерительных возможностей статистических критериев Из таблицы мы видим, что параметрические критерии могут оказаться несколько более мощными, чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. Однако лишь с некоторой натяжкой мы можем считать данные, представленные не в стандартизованных оценках, интервальными. Кроме того, проверка распределения «на нормальность» требует достаточно сложных расчетов, результат которых заранее неизвестен. Может оказаться, что распределение признака отличается от нормального и нам так или иначе все равно придется обратиться к непараметрическим критериям. Непараметрические критерии лишены всех этих ограничений и не требуют таких длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены лишь в одном: с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака. Эту задачу может решить только дисперсионный двухфакторный анализ 34

Этапы принятия статистического решения (по Е. В. Сидоренко): 1. Формулировка нулевой и альтернативной гипотез. 2. Определение объема выборки N. 3. Выбор соответствующего уровня значимости в зависимости от важности исследования – 0, 05; 0, 01; 0, 001. 4. Выбор статистического метода, который зависит от типа решаемой психологической задачи. 5. Вычисление соответствующего эмпирического значения по экспериментальным данным согласно выбранному статистическому методу. 6. Нахождение по таблицам критических значений для выбранного статистического метода соответствующих уровней значимости. 7. Построение оси значимости и нанесение на нее табличных критических значений и эмпирического значения. 8. Формулировка принятия решения (выбор Н 0 или Н 1). 9. На этом заканчивается принятие статистического решения. Но его необходимо перевести на психологический язык с помощью статистического вывода. 35

Место статистического вывода в общей последовательности проверки содержательной гипотезы (А. Д. Наследов): 1. Формулировка содержательной гипотезы. 2. Планирование исследования (выборка, процедура, инструментарий и т. д. ), в том числе предварительная формулировка доступной проверке статистической гипотезы. 3. Проведение измерений и накопление исходных данных. 4. Окончательная формулировка статистической гипотезы, выбор статистического критерия, установление величины α – допустимой вероятности ошибки I рода. 5. Определение р уровня статистической значимости в результате применения статистического критерия. 6. Статистический вывод: статистическое решение о принятии или отклонении Н 0. 7. Формулировка содержательного вывода. 36

Примечания Для каждого критерия разработан свой алгоритм расчетов. Современные статистические пакеты, такие как Statistica 6. 0, SPSS и др. , позволяют сделать расчёты быстро с применением графических средств представления результатов анализа. А. Д. Наследов отмечает, что при оформлении исследовательского отчета (курсовой или дипломной работы, публикации) статистические гипотезы и статистические решения, как правило, не приводятся. Обычно при описании результата указывают критерий, приводят необходимые описательные статистики (средние, сигмы, корреляции и т. д. ), эмпирические значения критериев, степени свободы и обязательно – р уровень значимости. Затем формулируют содержательный вывод в отношении проверяемой гипотезы с указанием (обычно в виде неравенства, например: р<0, 05) достигнутого или не достигнутого уровня значимости. 37

Пример возможного оформления: Формулировка статистической гипотезы о различиях. Выбор метода анализа (критерия различий). Статистическая гипотеза Н 0: Уровень выраженности признака в группе 1 не отличается от уровня выраженности признака в группе 2 Н 1: Уровень выраженности признака в группе 1 отличается от уровня выраженности признака в группе 2. Статистический метод Для проверки гипотезы можно выбрать Параметрический критерий для независимых выборок (т. к. проверка распределения показала соответствие нормальному): критерий Стьюдента для независимых выборок. Непараметрический критерий для независимых выборок (в случае если: нет возможности проверить распределение на соответствие нормальному такое соответствие установлено не для всех шкал все шкалы представлены в различных измерительных единицах) 38

