ОБОБЩЕНИЕ ВАРИАЦИОНН ЫХ РЯДОВ Абсолютные величины всегда

ОБОБЩЕНИЕ ВАРИАЦИОНН ЫХ РЯДОВ

Абсолютные величины всегда имеют свою единицу измерения (размерность), присущую изучаемому явлению. Широко распространены следующие виды единиц измерения: 1. натуральные, подразделяющиеся на простые (например, штуки, тонны, метры) и сложные (составные), представляющие собой комбинацию двух разноименных величин (например, киловаттчас) 2. усповно-натурапьные (например, алкогольные напитки учитываются в дкл 100% спирта, а различные виды топлива соизмеряют по условному топливу с теплотворной способностью 7000 ккал/кг или 29, 3 МДж/кг 1) 3. стоимостные, позволяющие соизмерить в денежной форме товары, которые нельзя соизмерить

Абсолютные величины Количество единиц с одинаковым значением признака обозначается f и называется частота. Очевидно, что, суммируя число всех единиц с одинаковыми значениями признака, получаем N

Относительные величины Относительная величина - это результат деления (сравнения) двух абсолютных величин. В числителе дроби стоит величина, которую сравнивают, а в знаменателе - величина, с которой сравнивают (база сравнения). Например, если сопоставить величины экспорта США и России, которые в 2005 году составили 904, 383 и 243, 569 млрд. долл. , соответственно, то относительная величина покажет, что величина экспорта США в 3, 71 раза (904, 383/243, 569) больше экспорта России, при этом базой сравнения является величина экспорта России.

Относительные величины Полученная относительная величина выражена в виде коэффициента, который показывает, во сколько раз сравниваемая абсолютная величина больше базисной. В данном примере база сравнения принята за единицу. В случае если основание принимается за 100, относительная величина выражается в процентах (%), а если за 1000 - в промилле (‰) Выбор той или иной формы относительной величины зависит от ее абсолютного значения

В средних величинах погашаются индивидуальные отклонения, соответствующие отдельным единицам совокупности. Чтобы средняя величина имела смысл, она должна рассчитываться для однородной совокупности

Исходное соотношение средней A/B • где А – объем изучаемого события в совокупности: это суммарная абсолютная величина; • В – объем совокупности: это число единиц совокупности. • ИСС дает нам уровень изучаемого события в расчете на единицу совокупности

Примеры средних • Средняя зарплата показывает, сколько получает один работник. Что же мы возьмем в числителе и знаменателе ИСС? А – сумма начисленных средств всем работникам = фонд зарплаты; В – численность работников

Примеры средних • Зарплата индивидуального работника – это индивидуальная величина. Фонд зарплаты – суммарная величина, а средняя зарплата – средняя величина

Примеры средних • Средняя цена показывает, сколько в среднем стоит данный товар. Что же мы возьмем в числителе и знаменателе ИСС? А – выручка от реализации всего товара = товарооборот; В – сколько единиц товара продано всего = количество проданного товара

Примеры средних • Средняя себестоимость показывает, сколько в среднем стоит производство единицы продукции. Что же мы возьмем в числителе и знаменателе ИСС? А – затраты на производство продукции = в экономической теории это называется издержками производства; В – выпуск продукции = количество произведенной продукции

Примеры средних • Средний возраст показывает, сколько в среднем лет исследуемой совокупности единиц, не обязательно одушевленных - это может быть средний возраст автомобилей, студентов, зданий, куриц. Что же мы возьмем в числителе и знаменателе ИСС? А – суммарное количество лет; В – количество обследуемых единиц

Примеры средних • Средняя продолжительность жизни, или средний срок службы показывает, сколько в среднем лет живет одушевленная единица совокупности и служит неодушевленная. Что же мы возьмем в числителе и знаменателе ИСС? А – суммарное количество лет жизни (службы); В – количество обследуемых единиц

Виды средних величин Математикой доказано, что большую часть средних, которыми мы пользуемся, можно выразить в общем виде формулой средней степенной

Средние величины, применяемые в статистике, относятся к классу степенных средних. Общая формула степенной средней имеет следующий вид: где _ x k – степенная средняя k-ого порядка; k – показатель степени, определяющий форму средней; х – варианты; n – количество вариант

Если k =1, получается средняя арифметическая:

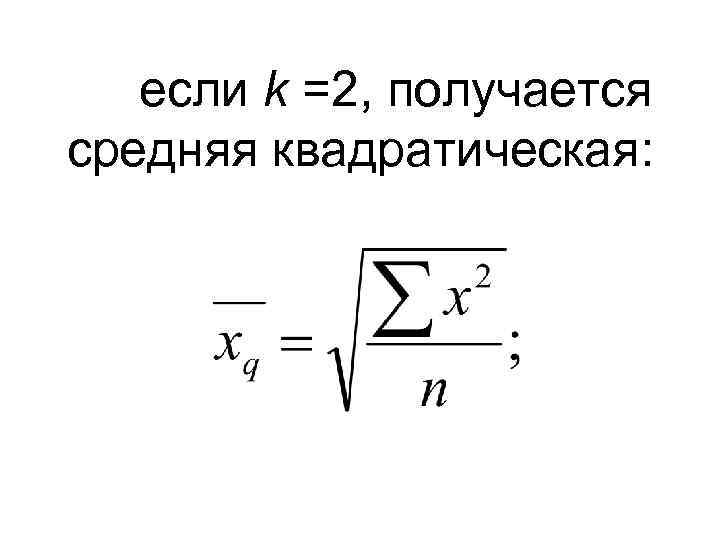
если k =2, получается средняя квадратическая:

если k =0, получается средняя геометрическая:

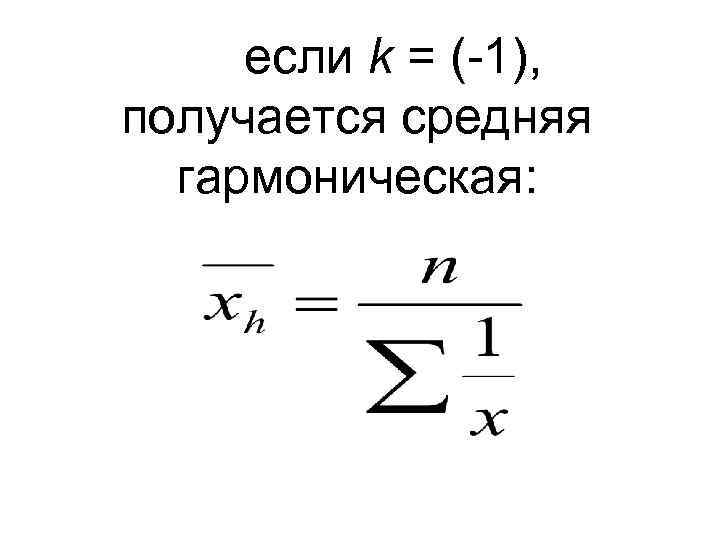
если k = (-1), получается средняя гармоническая:

Правило мажорантности Чем выше показатель степени в формуле степенной средней, тем больше значение средней

Средняя арифметическая

Существуют две формулы средней арифметической: где f - веса

Средняя арифметическая простая • Средняя арифметическая простая применяется, когда есть перечисление вариант и нет никаких группировок. В числителе мы собираем сумму вариант, в знаменателе – количество вариант

Производительность труда 5 -и рабочих составляет: 58, 50, 46, 44, 42 изделий за смену. Определить среднюю производительность труда 5 -и рабочих. В этом случае решение имеет следующий вид:

Средняя арифметическая взвешенная • Средняя арифметическая взвешенная используется при появлении группировок. Это самая распространенная степенная средняя

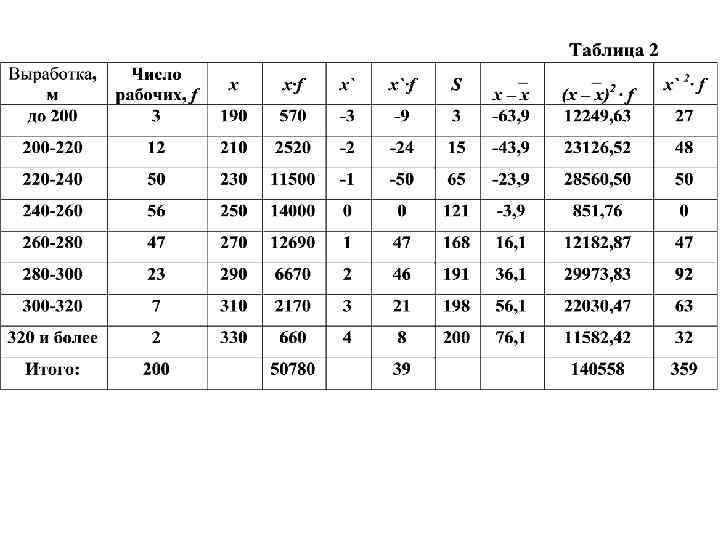
Расчет средней арифметической для вариационного ряда

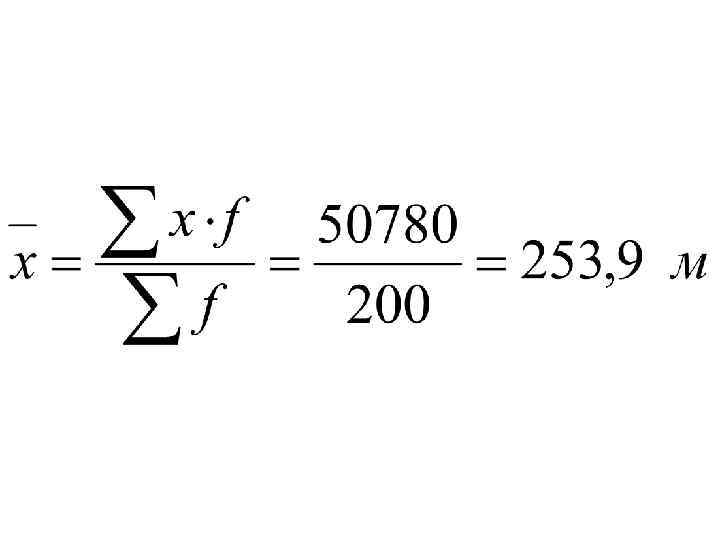
Свойства средней арифметической

1. Произведение средней арифметической и суммы частот равно общему объему изучаемого события в совокупности (см. формулу ИСС):

2. Сумма отклонений всех вариант от средней величины всегда равна 0:

2. Сумма отклонений всех вариант от средней величины всегда равна 0. Это значит, что в средней арифметической взаимопогашаются отклонения от средней

3. Если каждую варианту уменьшить на постоянную величину а, расчет средней возможен, но полученная средняя будет меньше на а:

4. Если все варианты уменьшить в одно и то же число раз, то средняя арифметическая уменьшится в то же число раз:

5. Если все веса разделить на какуюлибо константу а, то новая средняя от этого не изменится:

Средняя гармоническая

Средняя гармоническая • СГ- это обратная величина средней арифметической. Бывает простая и взвешенная СГ. Чаще используется взвешенная формула

Существуют две формулы для расчета средней гармонической величины: где W- сложный вес, объем события по группе, по конкретному значению

Сложный (мнимый) вес:

Средняя гармоническая применяется в том случае, когда в качестве весов выступают объемы изучаемого признака. Иногда возникает проблема: какую формулу использовать – среднюю гармоническую или среднюю арифметическую? Подходит та формула, у которой и в числителе и знаменателе будут величины, обладающие смыслом

Арифметическая или гармоническая? • Подсказка: • Если по исходной информации дается осредняемая величина (варианта) и знаменатель логической формулы, то используется САВ. • Если дается варианта и числитель логической формулы, то используется СГВ

Арифметическая или гармоническая? • Иными словами: • Если в ИСС неизвестен числитель, то используется САВ. • Если в ИСС неизвестен знаменатель, то используется СГВ

Структурные средние Обычно средней степенной для анализа распределения недостаточно. Структурные средние применяются для первоначального анализа распределения признаков в совокупности

Структурные средние Из многочисленного множества структурных средних мы рассмотрим моду, медиану, квартиль, дециль и перцентиль

Мода

Мода – значение признака, встречающееся в совокупности наибольшее число раз. В быту слово «мода» фактически имеет обратный смысл

Мода – это наиболее часто встречающаяся варианта вариационного ряда. Для дискретного ряда это та варианта, которой соответствует наибольшая частота

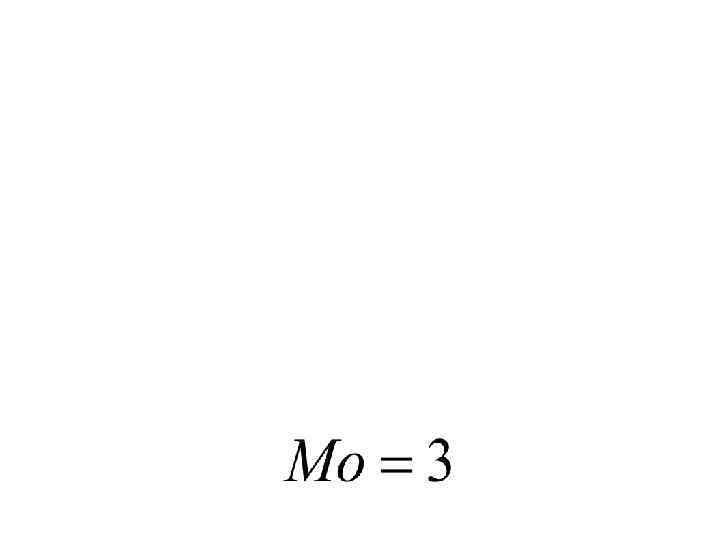
Для интервального ряда с равными интервалами мода определяется при помощи следующей формулы: где x. Mо - начало модального интервала; h. Мо - величина модального интервала; f 2 - частота модального интервала; f 1 - частота предмодального интервала; f 3 - частота послемодального интервала

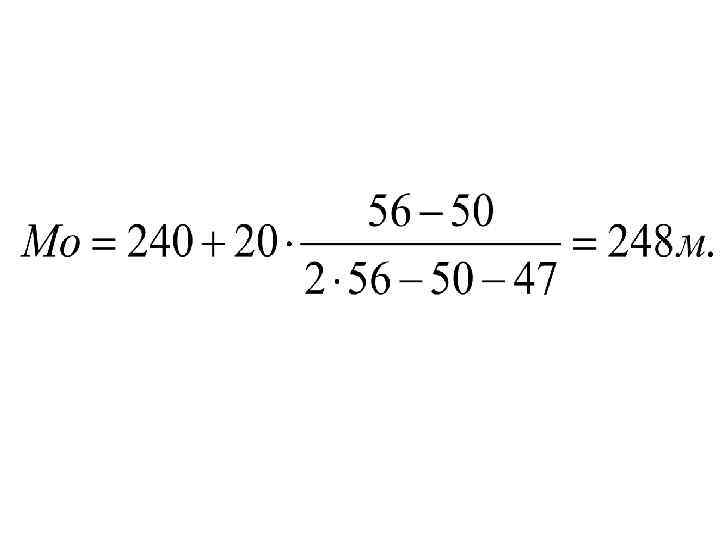
Мода • Если модальный интервал первый или последний, то недостающая частота (предмодальная или послемодальная) берется равной нулю

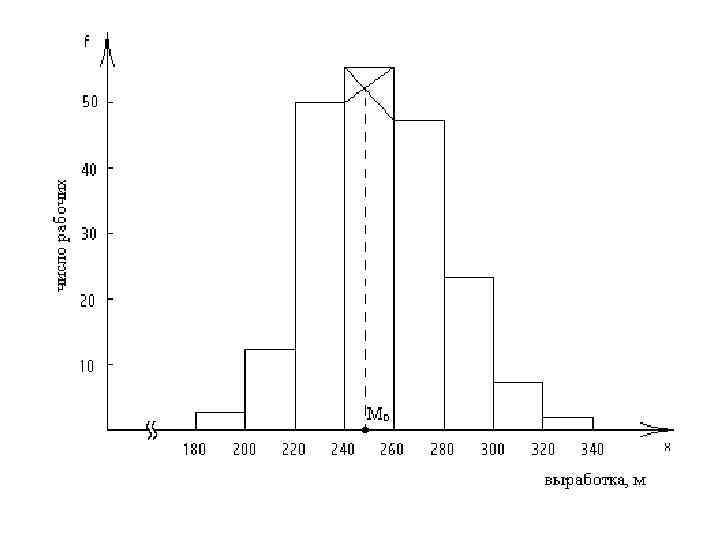
Мода • Для определения моды дискретного ряда строится полигон распределения. Расстояние от оси ординат до наивысшей точки графика есть мода

Мода • Если в дискретном ряду несколько вариант имеют наибольшую частоту (что встречается достаточно редко), то мода определяется как средняя арифметическая из всех модальных вариант

Медиана

Медиана • Это центральное, серединное значение ряда. Ме - значение признака у единицы, находящейся в середине ранжированной (упорядоченной) совокупности

Это варианта, лежащая в середине вариационного ряда и делящая его на две равные части

Медиана • В дискретном ряду Ме находится по определению, а в интервальном ряду – по формуле

Медиана • Если дискретный ряд содержит нечетное количество вариант, то находится та единственная варианта, справа и слева от которой находится одинаковое число вариант:

Для дискретного ряда медианой является та варианта, для которой накопленная частота впервые превышает половину от суммы частот

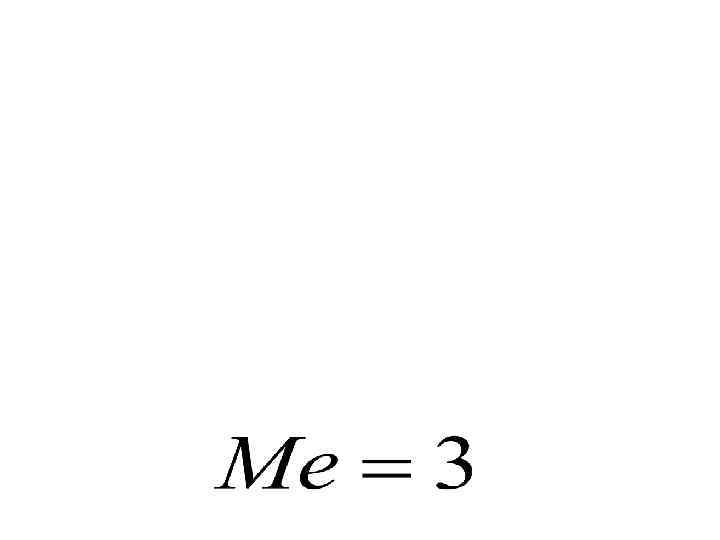
Для интервального ряда медиана определяется по следующей формуле: где x. Ме - начало медианного интервала; h. Ме - величина медианного интервала; f. Ме - частота медианного интервала; SМе-1 - накопленная частота предмедианного интервала

Это означает, что у половины рабочих производительность труда меньше 252. 5 м, а у другой половины больше

Для графического определения медианы последнюю ординату кумуляты делят пополам. Через полученную точку проводят прямую, параллельную оси x до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой представленного на графике распределения

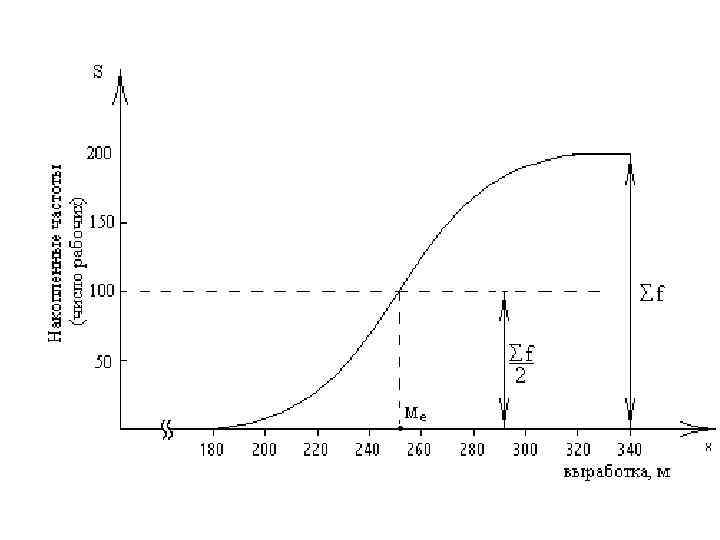
Для графического определения медианы по огиве выполняют обратные действия, поскольку в огиве накопленные частоты помещают на оси абсцисс, а значения признака – на оси ординат

Мо и Ме • В практических расчетах Мо и Ме могут быть величинами, далеко отстоящими друг от друга. Для более четкой фиксации характера распределения используют другие структурные средние

Квартили

Это варианты, которые делят ранжированную совокупность на четыре равные части: Q 1 Q 2 Q 3 1: 3; 2: 2 (Q 2=Ме); 3: 1

Квартили • Первый (нижний) квартиль отсекает от совокупности ¼ часть единиц с минимальными значениями, а третий (верхний) отсекает ¼ часть единиц с максимальными значениями

Квартили • Мы как бы отбрасываем нетипичные, случайные значения признака. С помощью квартилей мы определяем границы, где находятся 50% единиц, наиболее характерные для этой совокупности

Для расчета Q 1 (первого квартиля) используется следующая формула: где x. Q h. Q 1 1 SQ f. Q 1 -1 1 - начало интервала, содержащего 1 -й квартиль; - величина интервала, содержащего 1 -й квартиль; - накопленная частота предшествующего интервала; - частота интервала, содержащего Q 1

Интервалом, содержащим Q 1, является тот интервал, для которого накопленная частота впервые превышает ¼ от суммы частот

Это означает, что ¼ рабочих имеет производительность труда меньше, чем 234 м. , а ¾ имеет производительность труда больше

Для расчета Q 3 используется формула: Все обозначения аналогичны Q 1. Интервалом, содержащим Q 3 , является тот интервал, для которого накопленная частота впервые превышает ¾ от суммы частот

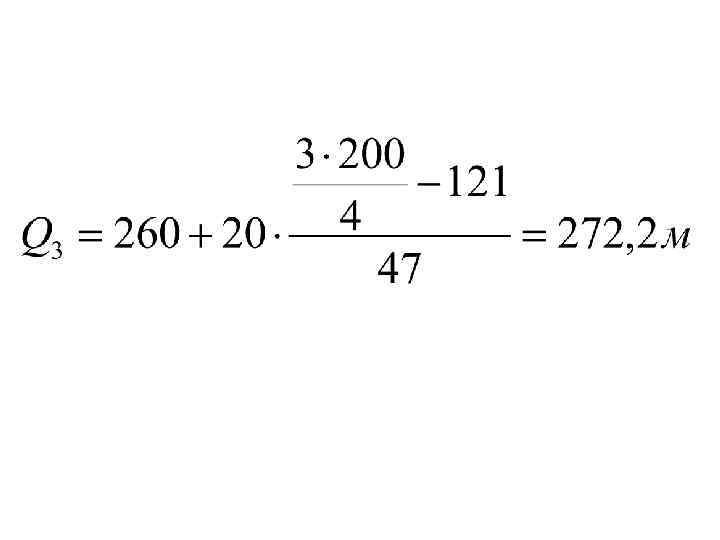
Децили

Децили это варианты, которые делят ранжированную совокупность на 10 равных частей

Общая формула для расчета децилей: где x. Di - начало интервала, содержащего i-й дециль; h Di - величина интервала, содержащего i-й дециль; f. Di - частота интервала, содержащего Di; SDi-1 - накопленная частота предшествующего интервала

Интервалом, содержащим Di , является тот интервал, для которого накопленная частота впервые превышает i/10 от суммы частот

Пример: Это означает что, 60% рабочих имеют производительность труда меньше 259, 6 м, а 40% больше

Применение децилей • Пример - децильный коэффициент дифференциации населения. Население делится на 10 частей по уровню дохода. Берут первые 10% и последние 10%. Считают, что средний доход последней группы не должен быть больше, чем в 10 раз среднего дохода первой группы. В России официально это превышение составляет 1416 раз, неофициально – 20 и более раз

Перцентиль • П делит ранжированную совокупность на 100 равных частей. Формулы аналогичны формулам медианы, квартиля и дециля

Показатели вариации

Определение вариации • Вариацией называется изменчивость значений признака у единиц статистической совокупности

Необходимость измерения вариации • При значительном рассеивании индивидуальных значений необходимо рассчитать специальную систему показателей, характеризующих средний размер отклонений индивидуальных значений от средней величины и степень колеблемости признака в совокупности, т. е. показателей вариации

Показатели вариации • Используются две группы показателей вариации: - абсолютные: размах вариации, среднее линейное отклонение, дисперсия, среднеквадратическое отклонение - относительные: коэффициент осцилляции, линейный коэффициент и коэффициент вариации

Ряды • • Простой ряд X 1 X 2 X 3 • • Взвешенный ряд X 1 f 1 X 2 f 2 X 3 f 3 • …. . • Xn • Xk fk » ------- » n

1. Размах вариации • РВ – разность между экстремальными значениями признака в совокупности. РВ имеет единицу измерения, совпадающую с единицей измерения признака у единиц совокупности

Размах вариации Недостаток РВ: он учитывает только крайние значения и не учитывает промежуточные значения

2. Среднее линейное отклонение Недостаток РВ устраняет показатель СЛО. Он рассчитывается по двум формулам: а) для несгруппированных данных (по формуле средней арифметической простой) б) для сгруппированных данных (по формуле средней арифметической взвешенной)

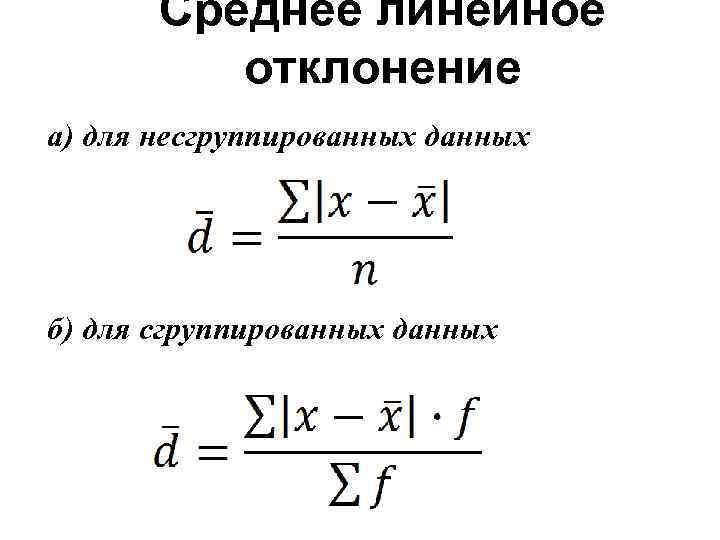
Среднее линейное отклонение а) для несгруппированных данных б) для сгруппированных данных

3. Дисперсия средний квадрат отклонений индивидуальных значений от средней величины. Это средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней. Она рассчитывается по простой и взвешенной формулам. Для ее обозначения используется греческая буква сигма.

Дисперсия а) для несгруппированных данных б) для сгруппированных данных

Расчет дисперсии для вариационного ряда

Осуществляется при помощи взвешенной формулы:

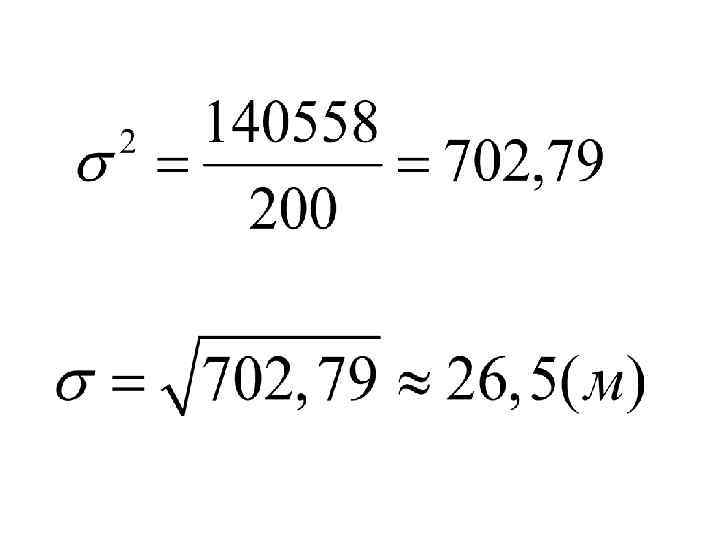
Свойства дисперсии

Свойства дисперсии • 1. Если все варианты увеличить на 2, то дисперсия…………………. • 2. Если все варианты увеличить в 2 раза, то дисперсия ………………. . • 3. Если все веса увеличить в 5 раз, то дисперсия………………….

1. Если из всех вариант вычесть какую-либо константу, то дисперсия от этого не изменится:

2. Если все варианты разделить на константу А, то дисперсия уменьшится от этого в А² раз:

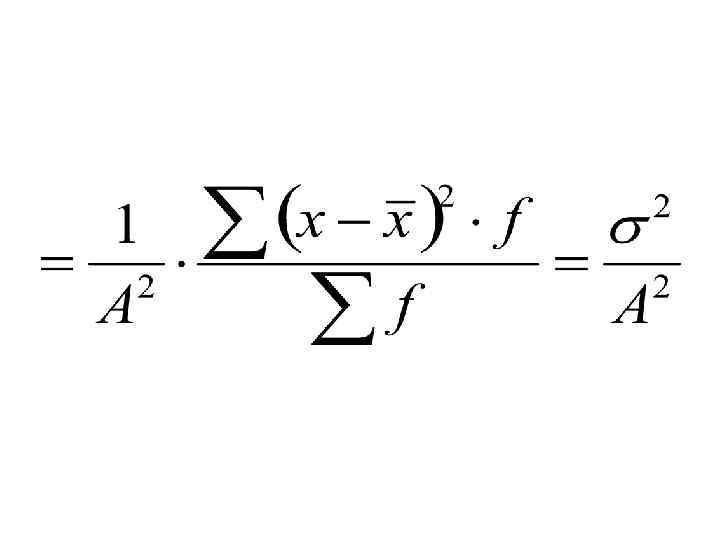
3. Дисперсия равна разности среднего квадрата вариант и квадрата их средней:

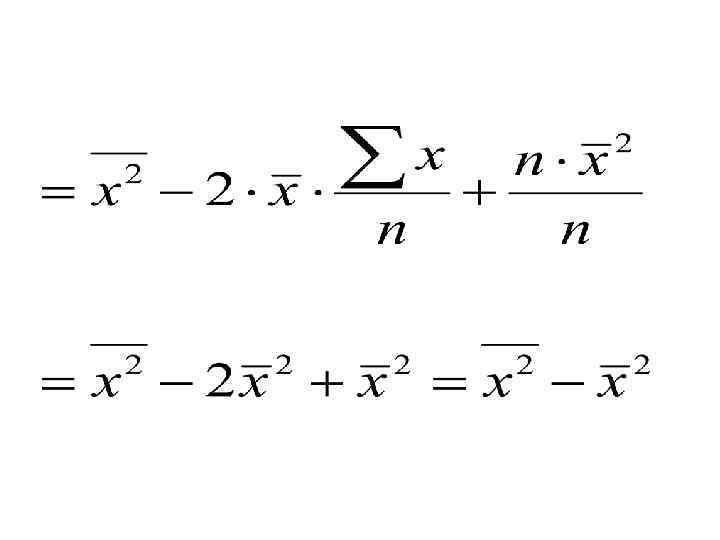
4. Если рассчитать среднее квадратическое отклонение от любой константы А, отличной от средней арифметической, то оно всегда будет больше дисперсии на квадрат разности между средней и данной константой А: , где

Недостаток дисперсии состоит в том, что она имеет размерность вариант, возведенную в квадрат (рублей в квадрате, человек в квадрате) Чтобы устранить этот недостаток, используется среднее квадратическое отклонение

4. Среднее квадратическое отклонение а) для несгруппированных данных

б) для сгруппированных данных σ представляет собой среднее квадратическое отклонение вариант ряда от средней величины

Среднее квадратическое отклонение имеет единицы измерения , а также может принимать положительные и отрицательные значения, поскольку получается в результате извлечения квадратного корня. С помощью СКО можно утверждать, что i-тое значение признака в совокупности находится в пределах:

Относительные показатели вариации

Относительные показатели вариации применяются для решения следующих задач: - сравнение степени вариации различных вариационных рядов - характеристика степени однородности совокупности

Коэффициент осцилляции где R - размах вариации - среднее значение

Коэффициент осцилляции отражает относительную колеблемость крайних значений признака относительно среднего значения

Линейный коэффициент вариации (относительное линейное отклонение) где - среднее линейное отклонение

Коэффициент вариации Характеризует долю усредненного значения отклонений от средней величины. При этом совокупность считается однородной, если V не превышает 33%

При V > 33% совокупность неоднородна, для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы. Требование к однородности данных присутствует практически во всех видах статистического анализа

Правило трех сигм

В условиях нормального распределения существует зависимость между величиной количеством наблюдений: в пределах σ и располагается 68, 3 % наблюдений; в пределах располагается 94, 5 % наблюдений в пределах располагается 99, 7 % наблюдений

На практике почти не встречаются отклонения, . которые превышают 3σ Отклонение в 3σ может считаться максимальным При помощи этого правила можно получить примерную оценку σ:

Дисперсия альтернативного признака

Признаки, которыми обладают одни единицы совокупности и не обладают другие, называются альтернативными. Количественно вариация альтернативного признака проявляется в значении 0 у единиц, которые им не обладают, или в значении 1 у единиц, которые им обладают

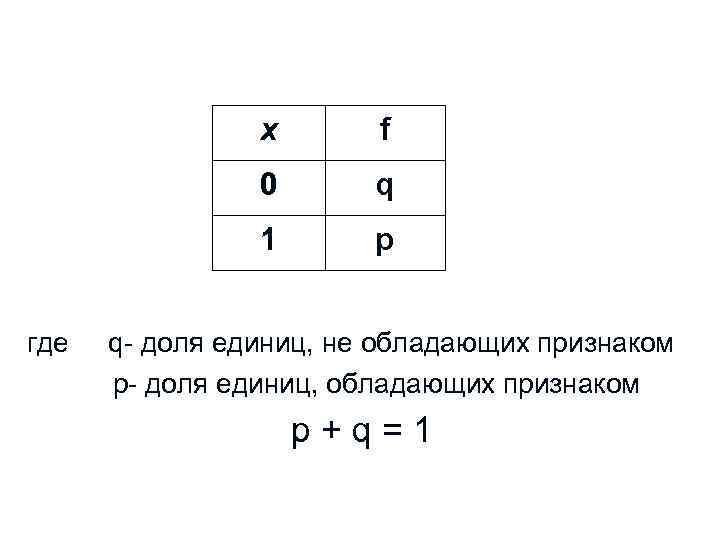
x 0 q 1 где f p q- доля единиц, не обладающих признаком p- доля единиц, обладающих признаком p+q=1

Среднее значение альтернативного признака

Дисперсия альтернативного признака : Максимальное значение дисперсии альтернативного признака 0, 25

Среднее квадратическое отклонение альтернативного признака : Коэффициент вариации альтернативного признака:

Правило сложения дисперсий

Выделяют дисперсии: 1) общую 2) межгрупповую 3) внутригрупповую

Величина общей дисперсии характеризует вариацию признака под воздействием всех факторов, вызывающих эту вариацию: где j – номер варианты

Межгрупповая дисперсия (дисперсия групповых средних или факторная дисперсия) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием одного фактора, положенного в основание группировки

гд е – среднее значение изучаемого признака для i –й группы – общая средняя для всей совокупности - номер группы – количество единиц в i – й группе

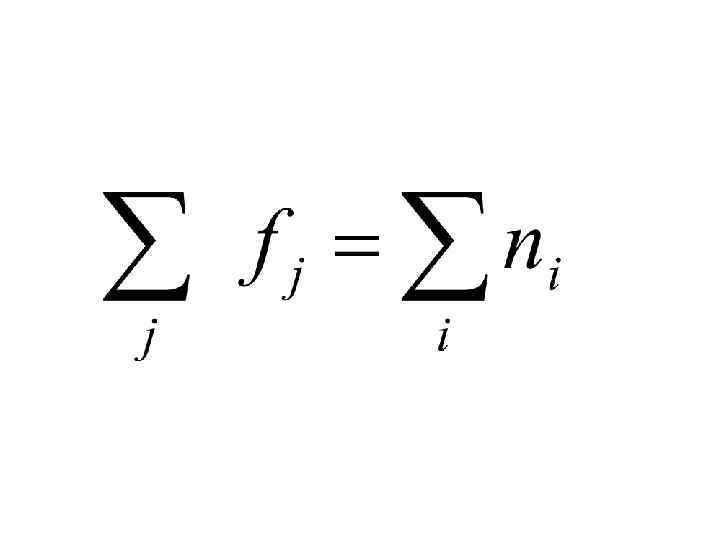
Внутригрупповая (средняя из групповых или остаточная) дисперсия характеризует случайную вариацию, т. е. ту часть вариации, которая вызвана действием других неучтённых факторов, и не зависящую от фактора, положенного в основании группировки:

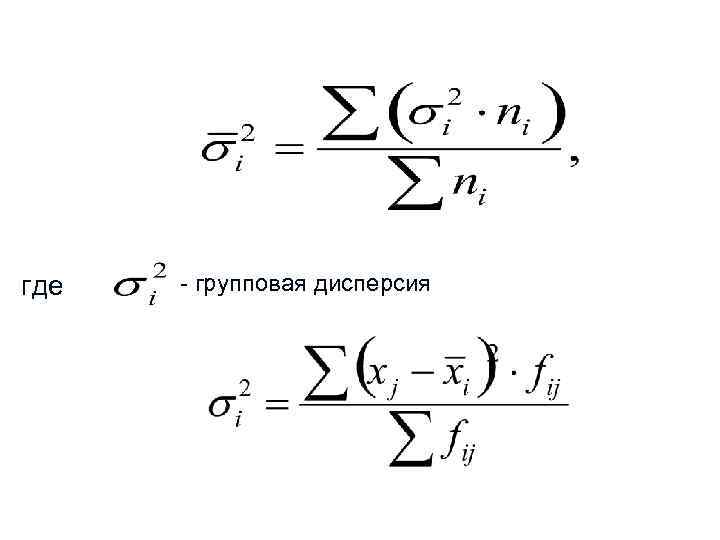
где - групповая дисперсия

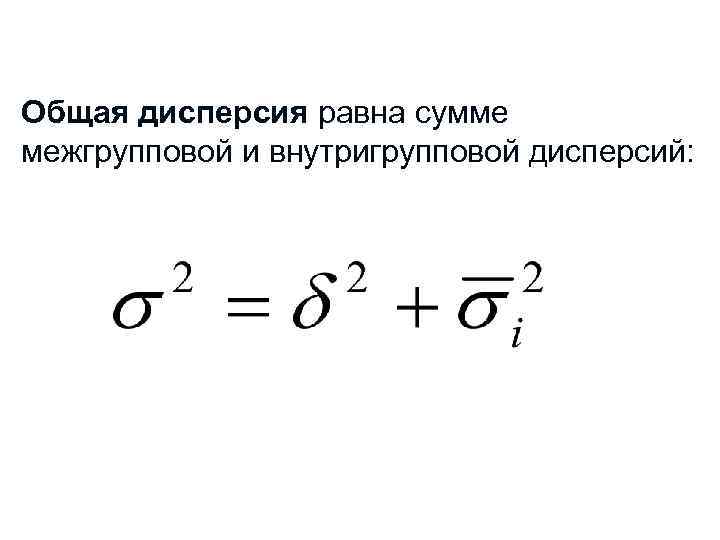
Общая дисперсия равна сумме межгрупповой и внутригрупповой дисперсий:

Эмпирический коэффициент детерминации: Эмпирический коэффициент детерминации показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака (факторного)

Эмпирическое корреляционное отношение : Эмпирическое корреляционное отношение характеризует степень влияния группировочного признака на результативный показатель. Эмпирическое корреляционное отношение изменяется в пределах от -1 до 1. Чем ближе IηI к единице, тем степень влияния больше -1 ≤ η ≤ 1

Моменты распределения

Обобщающие характеристики вариационного ряда могут быть представлены системой величин, носящих название моментов распределения

Формула момента k-го порядка: где: x – варианты k – показатель степени f – частоты А – const

1. При А = 0 получаем систему начальных моментов. Начальный момент k-го порядка выражается формулой: Начальный момент первого порядка равен

2. При А = получаем систему центральных момент Центральный момент k-го порядка выражается формулой: Центральный момент первого порядка равен 0 Центральный момент второго порядка равен σ²

При А = где: получаем систему условных моментов: – некоторый вариант ряда, обычно близкий к его середине

Нормированный момент представляет собой отношение центрального момента k-го порядка к kой степени среднего квадратического отклонения:

Нормированный момент - первого порядка равен 0 - второго порядка равен 1 - третьего и четвертого порядков используется для характеристики асимметрии и эксцессов

Показатели асимметрии и эксцесса

Симметричным называется такое распределение, при котором варианты, равноотстоящие от средней, имеют равные частоты. Если распределение асимметрично, частоты вариантов, равноотстоящих от средней, не равны между собой

Для характеристики асимметрии используется нормированный момент третьего порядка: Если А = 0 распределение симметрично Если А > 0 имеет место правосторонняя асимметрия Если А < 0 имеет место левосторонняя асимметрия

Под эксцессом понимается степень островершинности распределения, при этом в качестве эталона берется нормальное распределение. Характеристикой эксцесса является нормированный момент четвертого порядка

Формула коэффициента эксцесса:

Для нормального распределения Е = 0. Для более островершинных распределений, чем нормальное, Е > 0, для более плосковершинных Е < 0

Свойства выборочных оценок • Несмещенность – математическое ожидание равно истинному значению • Эффективность – наименьшая дисперсия • Состоятельность – стремление по вероятности к истинному значению

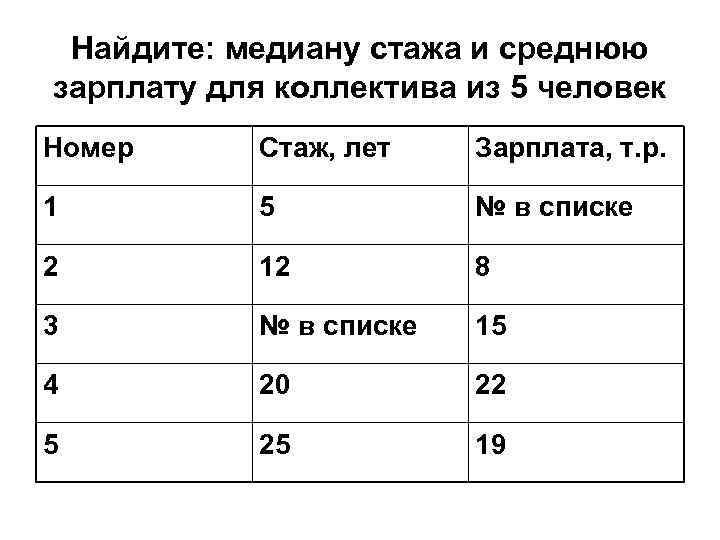
Найдите: медиану стажа и среднюю зарплату для коллектива из 5 человек Номер Стаж, лет Зарплата, т. р. 1 5 № в списке 2 12 8 3 № в списке 15 4 20 22 5 25 19

• Спасибо за внимание