Обмінна взаємодія Обмінна взаємодія є результатом кулонівської

Обмінна взаємодія

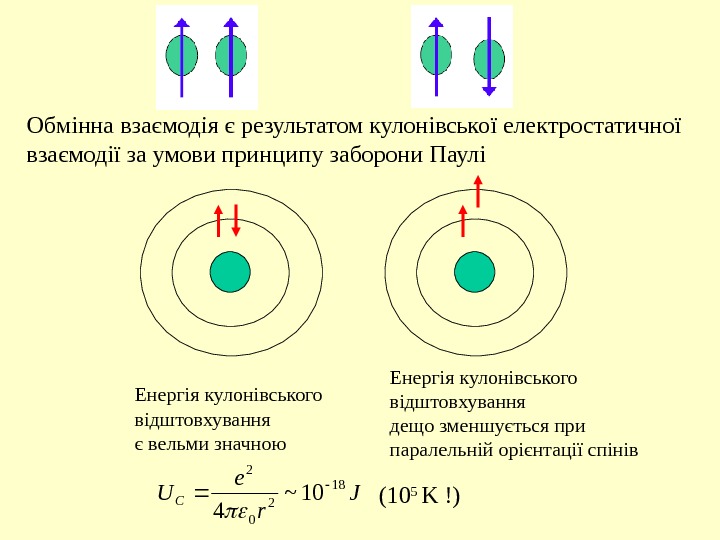
Обмінна взаємодія є результатом кулонівської електростатичної взаємодії за умови принципу заборони Паулі Енергія кулонівського відштовхування є вельми значною. J r e U C 18 2 0210~ 4 (10 5 K !)Енергія кулонівського відштовхування дещо зменшується при паралельній орієнтації спінів

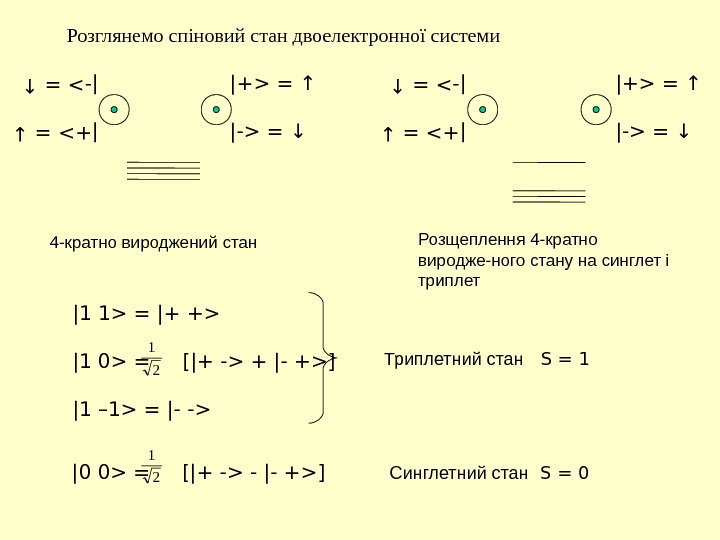
|+> = ↓ |-> = ↑Розглянемо спіновий стан двоелектронної системи 4 -кратно вироджений стан |+> = ↓ |-> = ↑ |+> = ↑ |-> = ↓ Розщеплення 4 — кратно виродже-ного стану на синглет і триплет |1 1> = |+ +> |1 0> = [|+ -> + |- +>] |1 – 1> = |- -> Триплетний стан S = 1 |0 0> = [|+ -> — |- +>] Синглетний стан S = 0 2 1|+> = ↑ |-> = ↓

Розглянемо рух двох електронів у атомі : +r 1 r 21 2 Zee — e -r 12 1202 20 2 22 10 2 12 1221 4 42 42 re r. Ze m ee 12 21 HHHH Гамільтоніан : 22 22 22 jjjj zyx

Застосування одноелектронного наближення : )()()()( )1(2 1 ), ( 21122211 221 rrrr srr As синглет триплет21 , — нормалізовані просторові одноелектронні хвильові функції )()( )1(2 1 ), (211221 rrrr s rrs )()( 1211 rrs інтеграл перекривання

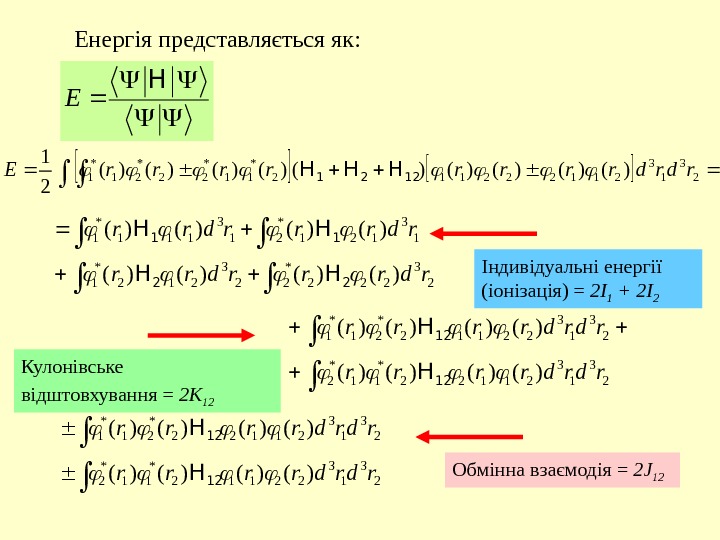
H E 23 13 211222112* 11* 22* 21* 1 )()()()()( 21 rdrdrrrr. E 1221 HHHЕнергія представляється як : 23 222* 223 212* 1 13 121* 213 111* 1 )()()()( rdrrrdrr 22 11 HH HH 23 13 21122* 11* 2 23 13 22112* 21* 1 )()()()( rdrdrrrr 1212 HH 23 13 22112* 11* 2 23 13 21122* 21* 1 )()()()( rdrdrrrr 1212 HH Індивідуальні енергії ( іонізація ) = 2 I 1 + 2 I 2 Кулонівське відштовхування = 2 K 12 Обмінна взаємодія = 2 J

121221 JKIIEМожна представити енергію як : Найнижчий енергетичний стан для триплету: 121221 JKIIE При паралельній орієнтації спінів енергія зменшується на : 2 3 1 3 2112 21 2 * 21 * 1 0 2 12)()( 1 )()( 4 rdrdrr rr rr e J ( якщо J 12 додатній)

Можна підставити спінову хвильову функцію у явному вигляді у попередній вираз : )2()1( )1()2()2()1( )()( 21 ), ( )1()2()2()1()()( 21 ), ( 2112221121 rrrrrr As ( синглет ) ( триплет ) 1 0 01 Спін +1/2 Спін -1/

12 4 22 )1( )(2 )0()1(J s Qs. K SESE Різниця енергій триплетного і синглетного станів : )()( 1211 rrs )()( 2211122211 rr. Hrr. Q )()( 2112122211 rr. Hrr. K інтеграл перекривання кулонівський інтеграл обмінний інтеграл Якщо s = 0 , тоді 12 JK

, 2, S Спін-гамільтоніан Гейзенберга-Дірака-Ван Флека ( HDVV): jiex. SSJ 2 H( спінова матриця Паулі )Модель Гейзенберга J – параметр обмінної взаємодії ( обмінний інтеграл )Гейзенберг та Дірак продемонстрували, що 4 вищерозглянутих спінових стани є власними значеннями оператора 21 SS

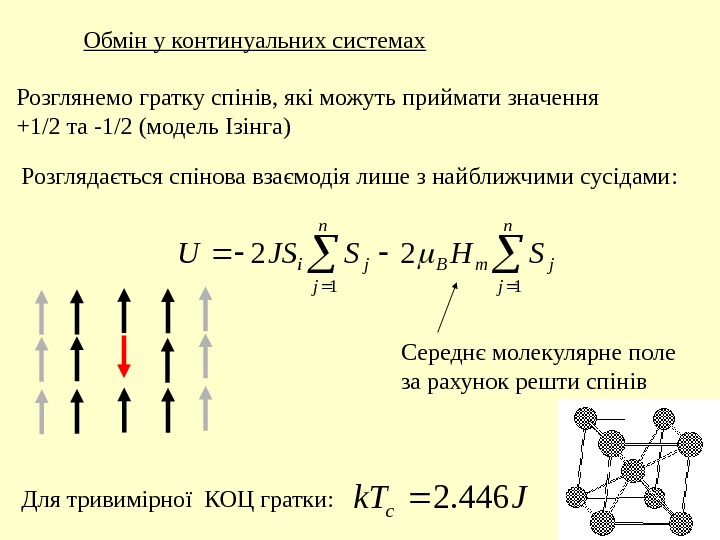
Розглянемо гратку спінів, які можуть приймати значення +1/2 та -1/2 ( модель Ізінга ) Розглядається спінова взаємодія лише з найближчими сусідами : n j jm. Bji SHSJSU 11 22 Середнє молекулярне поле за рахунок решти спінів Для тривимірної КОЦ гратки : Jk. T c 446. 2 Обмін у континуальних системах

Оцінка величини параметру обмінної взаємодії J r a : радіус атому r 3 d : радіус 3 d комірки Крива Бете-Слейтера Співвідношення r a /r 3 d визначає обмінний інтеграл Mn +3 : антиферомагнітна Приклади: Mn. Bi, Cu 2 Mn. Sn, Cu 2 Mn. Al ( сплави Гойслера )

Обмінна взаємодія у молекулярних системах Димери Молекулярна будова моногідрату ацетату міді(ІІ) Cu 2 (CH 3 COO) 4 · 2 H 2 O Експериментальні та розраховані значення магнітної сприйнятливості моногідрату ацетату міді(ІІ)

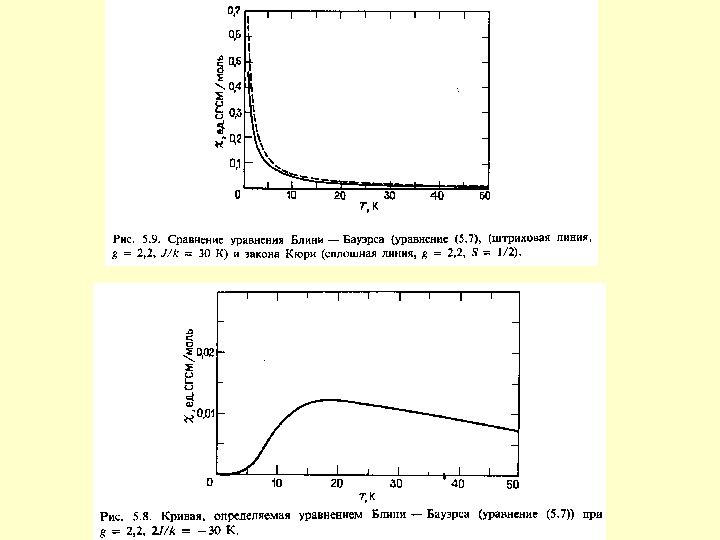
Рівняння Бліні-Бауерса n nn nnn k. TEEk. TEN )/exp(]2/)[( 0 0)2(2)1( E 1 = 0 E 2 = g B H E 3 = 2 J E 4 = -g B H

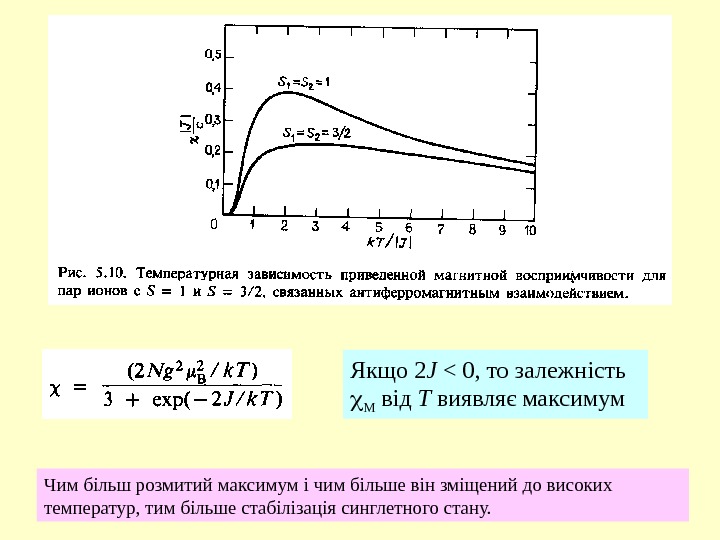
Якщо 2 J < 0, то залежність M від T виявляє максимум Чим більш розмитий максимум і чим більше він зміщений до високих температур, тим більше стабілізація синглетного стану.

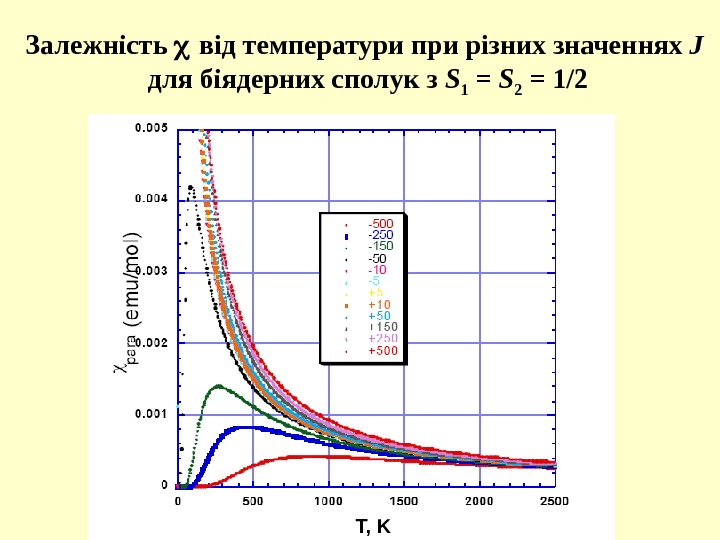
Залежність від температури при різних значеннях J для біядерних сполук з S 1 = S 2 = 1/2 T, K

Залежність добутку Т від температури при різних значеннях J T, K

Залежність від температури при різних значеннях J (антиферомагнітна взаємодія) 1. При проведенні апроксимації експериментальних даних необхідно використовувати залежність від Т, оскільки наявність максимуму робить цю залежність дуже чутливою до зміни величини J при невеликих та помірних значеннях J. 2. При великих абсолютних значеннях J його розрахунок завжди є приблизним і з досить великою похибкою. T, K

Залежність добутку Т від температури при різних значеннях J (антиферомагнітна взаємодія) 1. Чим більше за абсолютним значенням J , тим нижче лежить крива і тим більше її нахил. 2. Відсутність максимуму унеможливлює точну апроксимацію експериментальних даних. 3. Оскільки при температурах, близьких до нуля, добуток Т фактично дорівнює нулю, експериментально виміряна сприйнятливість зразка має бути дуже чутливою до присутності домішок. T, K

Залежність від температури при різних значеннях J (феромагнітна взаємодія) J = 0, +10, +20, +50, +200 см -1 Для різних J графіки практично не відрізняються. T, K

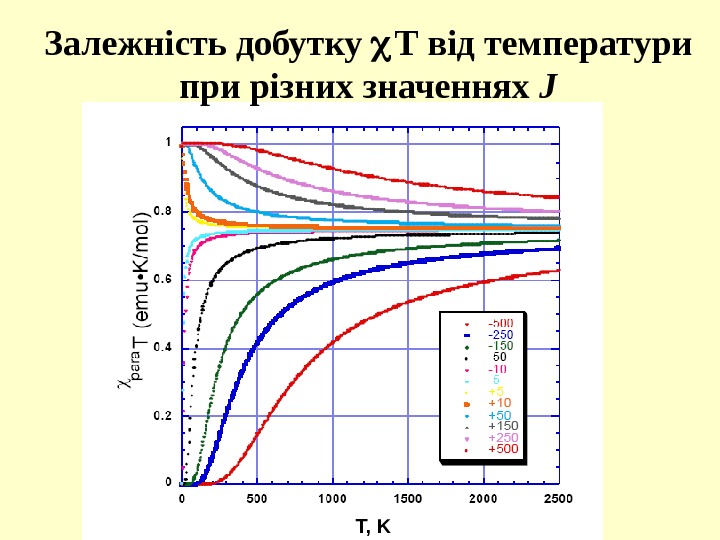
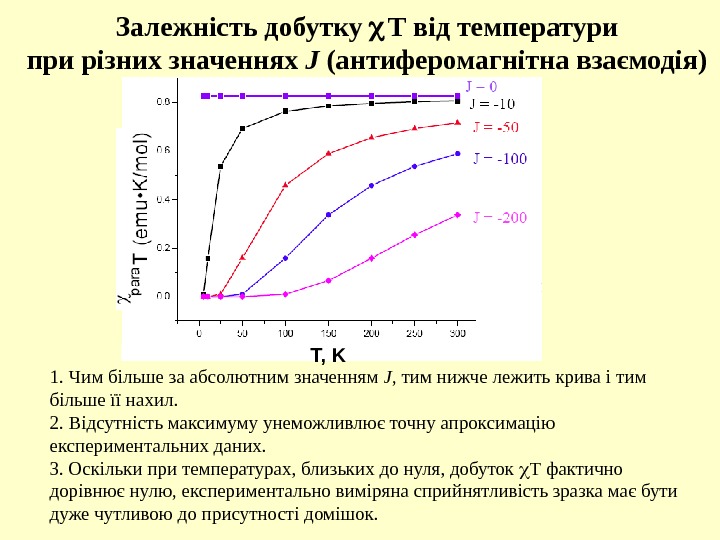
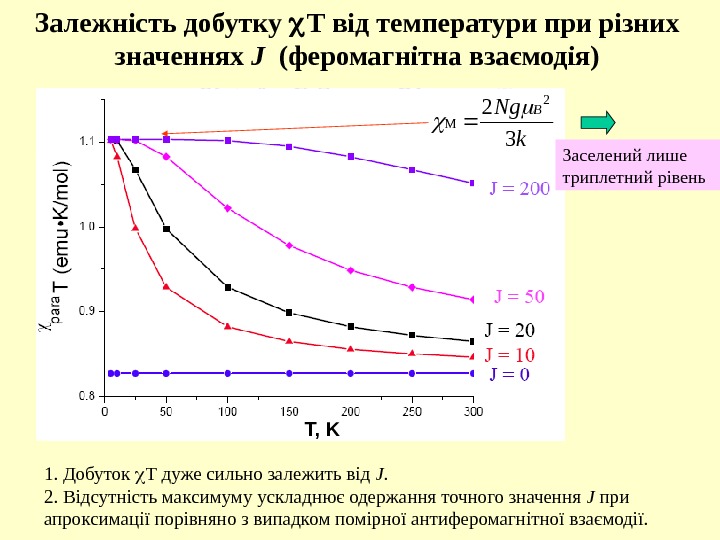
Залежність добутку Т від температури при різних значеннях J (феромагнітна взаємодія) 1. Добуток Т дуже сильно залежить від J. 2. Відсутність максимуму ускладнює одержання точного значення J при апроксимації порівняно з випадком помірної антиферомагнітної взаємодії. T, K k. Ng B 32 2 M Заселений лише триплетний рівень

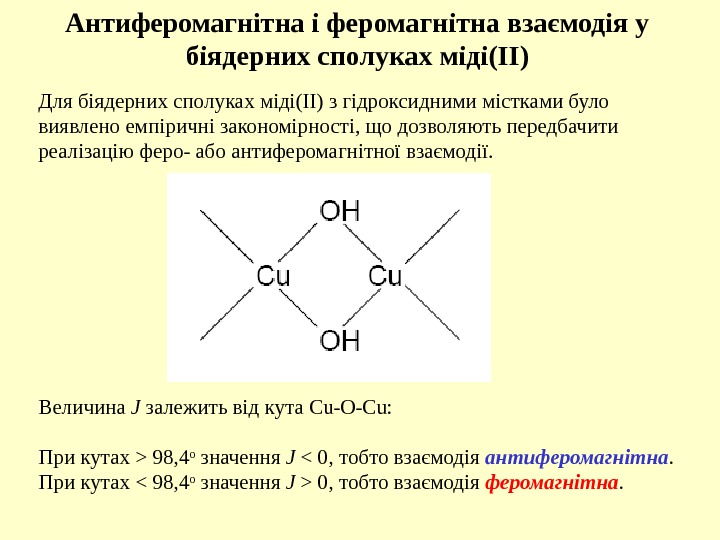
Антиферомагнітна і феромагнітна взаємодія у біядерних сполуках міді(ІІ) Для біядерних сполуках міді(ІІ) з гідроксидними містками було виявлено емпіричні закономірності, що дозволяють передбачити реалізацію феро- або антиферомагнітної взаємодії. Величина J залежить від кута Cu-O-Cu: При кутах > 98, 4 o значення J < 0, тобто взаємодія антиферомагнітна. При кутах 0, тобто взаємодія феромагнітна.

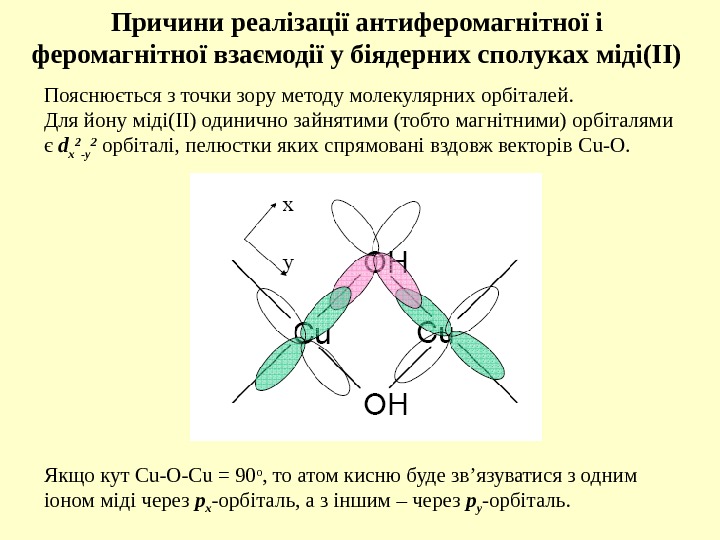
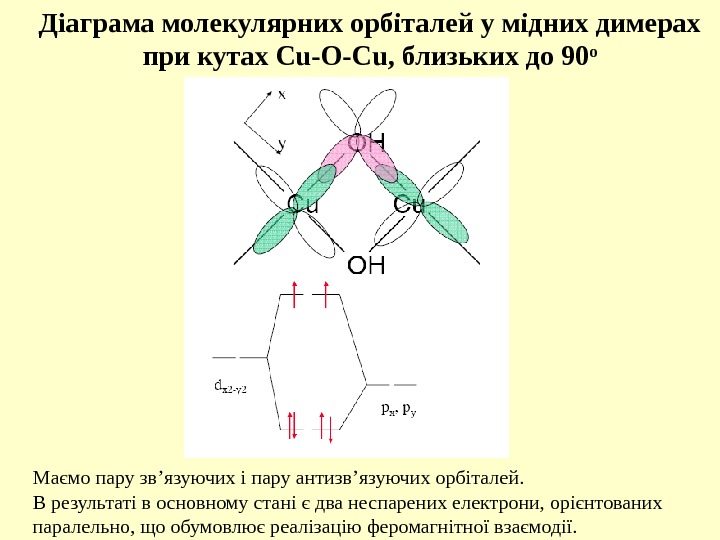
Якщо кут Cu-O-Cu = 90 o , то атом кисню буде зв ’ язуватися з одним іоном міді через p x — орбіталь, а з іншим – через p y -орбіталь. Причини реалізації антиферомагнітної і феромагнітної взаємодії у біядерних сполуках міді(ІІ) Пояснюється з точки зору методу молекулярних орбіталей. Для йону міді(ІІ) одинично зайнятими (тобто магнітними) орбіталями є d x 2 -y 2 орбіталі, пелюстки яких спрямовані вздовж векторів Cu-O.

Діаграма молекулярних орбіталей у мідних димерах при кутах Cu-O-Cu, близьких до 90 о Маємо пару зв ’ язуючих і пару антизв ’ язуючих орбіталей. В результаті в основному стані є два неспарених електрони, орієнтованих паралельно, що обумовлює реалізацію феромагнітної взаємодії.

Діаграма молекулярних орбіталей у мідних димерах при кутах Cu-O-Cu, близьких до 180 о В даному випадку атоми кисню використовую лише одну орбіталь Оскільки у взаємодії приймають участь лише по одній орбіталі від атомів міді та кисню, маємо пару орбіталей (зв ’ язуючу і антизв ’ язуючу), на якій розміщуються чотири електрони. В результаті в основному стані усі електрони є спареними, що обумовлює реалізацію антиферомагнітної взаємодії.

Причини реалізації антиферомагнітної і феромагнітної взаємодії у мідних димерах Наведені приклади демонструють граничні випадки (для кутів Cu-O-Cu = 90 o і 180 o. Перший випадок (феромагнітна взаємодія при куті 90 о ) є специфічним випадком реалізації принципу ортогональності орбіталей : якщо неспарені електрони знаходяться на ортогональних орбіталях (або, іншими словами, якщо магнітні орбіталі розташовані перпендикулярно), тоді взаємодія буде феромагнітною. Кут 98, 4 о є граничною величиною лише для площинних гідроксидних містків в димерних сполуках міді(ІІ). Для інших систем з одноатомними містками справедливою є загальна закономірність: чим більш тупий кут на містковому атомі, тим сильніше антиферомагнітна взаємодія.

Чим визначається знак J ? J F пропорційний обмінному інтегралу між 1 та 2 ( J 12 ) J AF пропорційний квадрату інтегралу перекривання між 1 та 2 ( s 12 ) J 12 залежить від ступеня (площі) перекривання, незалежно від знаку перекривання s 12 залежить від балансу між областями позитивного і негативного перекривання Якщо “+” = “-”, тоді s 12 = 0. У цьому випадку молекулярні орбіталі розташовані ортогонально, і взаємодія феромагнтіна. При цьому чим більше ступінь перекривання, тим більше стабілізація триплетного стану.

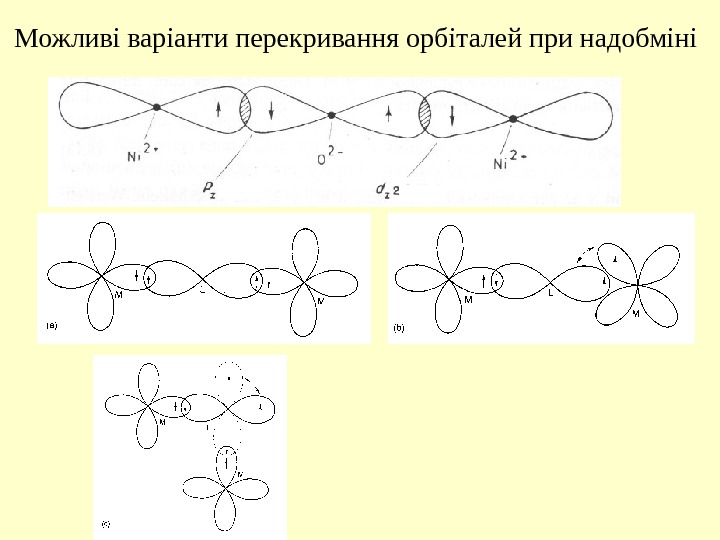
Можливі варіанти перекривання орбіталей при надобміні

Принцип ортогональності магнітних орбіталей антиферомагнітна взаємодія: t 2 g — t 2 g феромагнітна взаємодія: t 2 g — e g антиферомагнітна взаємодія: t 2 g — t 2 g та t 2 g — e g

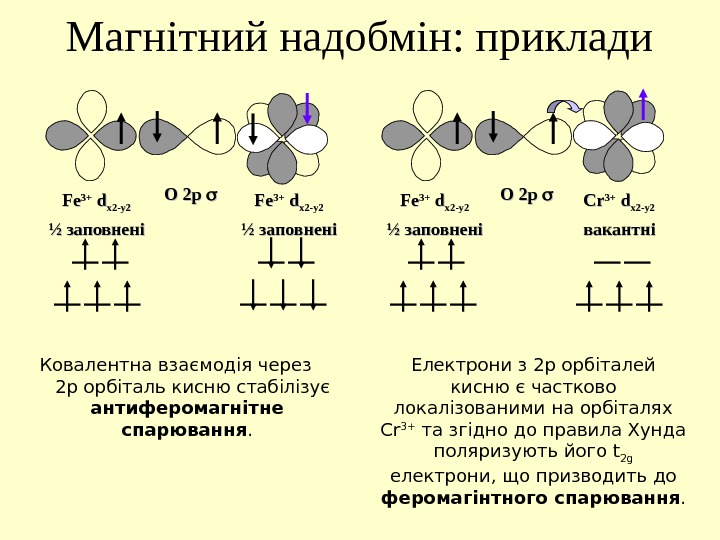
Магнітний надобмін: приклади Fe. Fe 3+3+ d d x 2 -y 2 x 2 -y 2 ½ ½ заповненізаповненіO 2 p Ковалентна взаємодія через 2 p орбіталь кисню стабілізує антиферомагнітне спарювання. Fe 3+3+ d d x 2 -y 2 ½ ½ заповнені Cr. Cr 3+3+ d d x 2 -y 2 вакантніO 2 p Електрони з 2 p орбіталей кисню є частково локалізованими на орбіталях Cr 3+ та згідно до правила Хунда поляризують його t 2 g електрони, що призводить до феромагінтного спарювання.

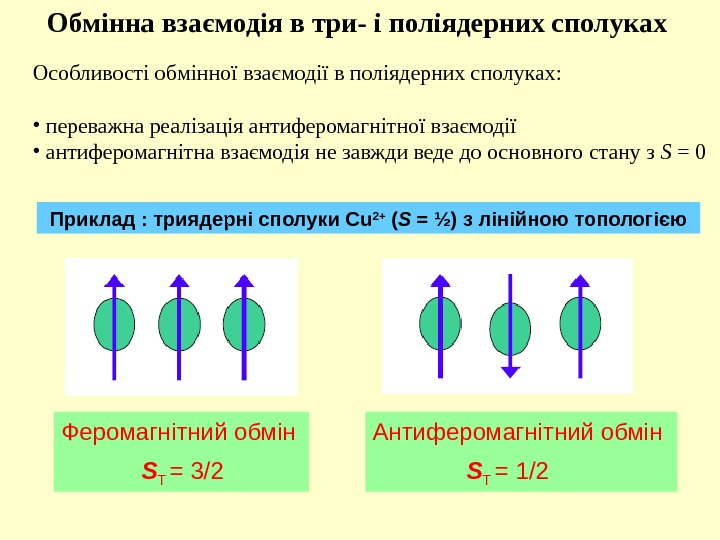
Обмінна взаємодія в три- і поліядерних сполуках Особливості обмінної взаємодії в поліядерних сполуках: • переважна реалізація антиферомагнітної взаємодії • антиферомагнітна взаємодія не завжди веде до основного стану з S = 0 Феромагнітний обмін S T = 3/2 Антиферомагнітний обмін S T = 1 /2 Приклад : триядерні сполуки Cu 2+ ( S = ½) з лінійною топологією

• феромагнітний обмін завжди веде до більшого значення S T , але антиферомагнітний обмін може призводити до досить великого S T ( за умови належного розташування магнітних орбіталей) Обмінна взаємодія в три- і поліядерних сполуках Приклад : триядерні сполуки Mn 2+ Cu 2+ Mn 2+ з лінійною топологією Mn 2+ ( S = 5/2)Cu 2+ ( S = 1/2) Сумарний спін S T = 9/

Обмінна взаємодія в три- і поліядерних сполуках • для сполук з непарною кількістю парамагнітних частинок за умов кутової топології можливий прояв спінової фрустрації ( невизначеності ) Приклад : триядерні сполуки Cu 2+ ( S = ½) з топологією плоского трикутника (симетрія С 3 і вище) і антиферомагнітною взаємодією між сусідніми іонами міді S T = 1 /2 Таким чином, обмінна взаємодія в одній з трьох пар іонів міді буде вимушено феромагнітною , але залишається невизначеним, в якій саме парі.

Обмінна взаємодія у високоядерних обмінних кластерах • в більшості відомих високоспінових обмінних кластерів спостерігається переважна реалізація антиферомагнітного обміну • можлива реалізація як тотальної феромагнітної взаємодії, так і антиферомагнітної взаємодії з високим сумарним спіном. Приклад : усі похідні кластерів Mn 12 , Fe 14 , Fe 19 , Cr 12 Приклад : 7 — ядерний обмінний кластер міді(ІІ) Феромагнітний обмін S T = 7 /2 Антиферомагнітний обмін S T = 5 /

Обмінна взаємодія у високоядерних обмінних кластерах • можлива реалізація більш ніж одного шляху надобміну, наслідком чого стає необхідність введення більш ніж одного параметру обмінної взаємодії ( J ) J 1 J 2 Приклад : 7 — ядерний кластер з топологію правильного шестикутника, в середині якого розташований сьомий парамагнітний центр Два параметри обмінної взаємодії: J 1 – обмін між термінальними йонами J 2 – обмін між центральним і термінальними йонами

Обмінна взаємодія у високоядерних обмінних кластерах • розділення внесків від різних параметрів обмінної взаємодії може бути досить важкою задачею. Якщо один з параметрів значно переважає інші за абсолютною величиною, то внесок інших може бути практично знівельованим. Приклад: J 1 – слабко антиферомагнітна взаємодія J 2 – сильно антиферомагнітна взаємодія Результат : S T = 5/2 Таким чином, J 1 долає J 2 , що спіни термінальних іонів розташовуватися паралельно. При цьому не має значення, чи буде взаємодія між термінальними центрами ( J 2 ) феро- або антиферомагнітною. J 1 J

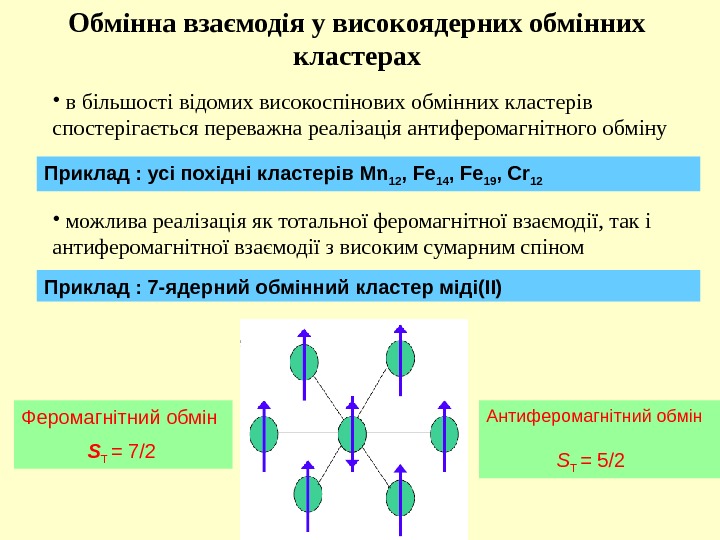
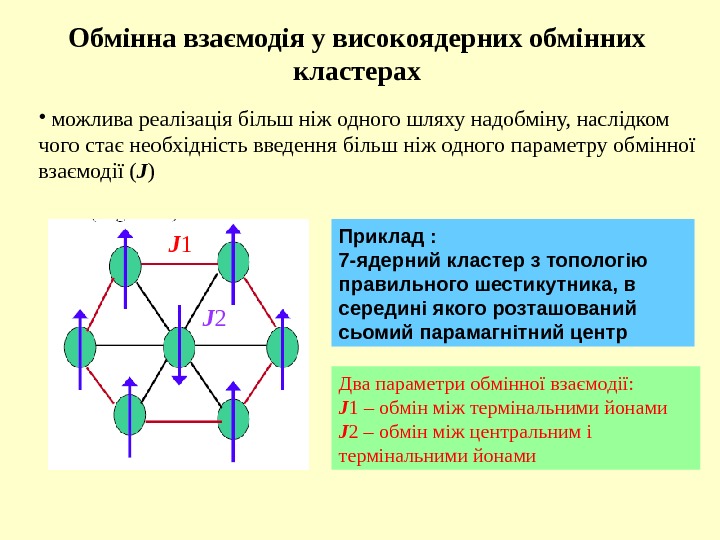
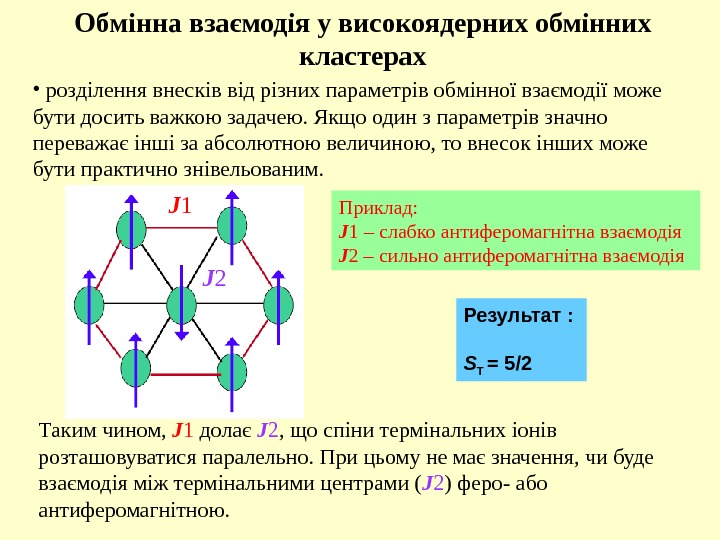
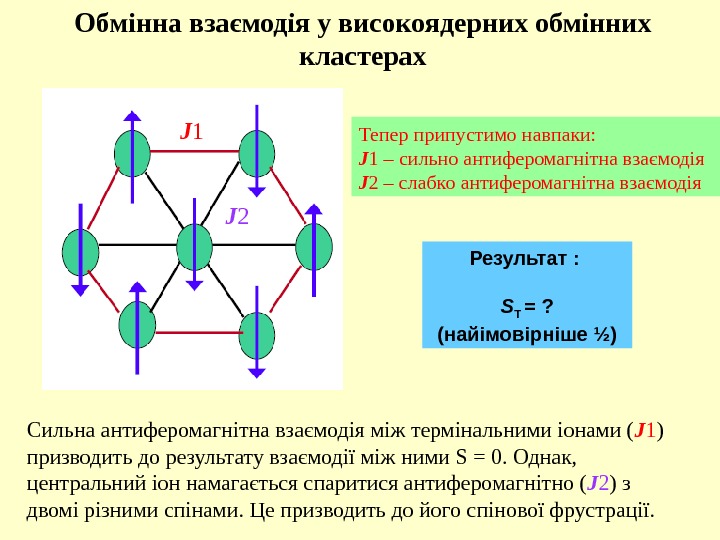
Обмінна взаємодія у високоядерних обмінних кластерах J 1 J 2 Тепер припустимо навпаки: J 1 – сильно антиферомагнітна взаємодія J 2 – слабко антиферомагнітна взаємодія Результат : S T = ? (найімовірніше ½) C ильна антиферомагнітна взаємодія між термінальними іонами ( J 1 ) призводить до результату взаємодії між ними S = 0. Однак, центральний іон намагається спаритися антиферомагнітно ( J 2 ) з двомі різними спінами. Це призводить до його спінової фрустрації.

Додекаядерний обмінний кластер нікелю Ni 10 ( S T = 12) 1. Добуток Т ніколи не зменшується, а тільки збільшується. Це свідчить про наявність феромагнітної взаємодії. 2. Добуток Т є вельми близьким до величин, розрахованих за законом Кюрі (червона лінія). Це свідчить про те, що обмінна взаємодія досить слабка. 3. При низьких температурах добуток Т не досягає розрахованої величини для S T = 1 2. Це підтверджує висновок про те, що феромагнітна взаємодія є слабкою, навіть при 1, 8 К збуджені стани все ще є заселеними. 4. Більш важливою для встановлення типу обмінної взаємодії є форма кривої, а не значення Т при низьких температурах.

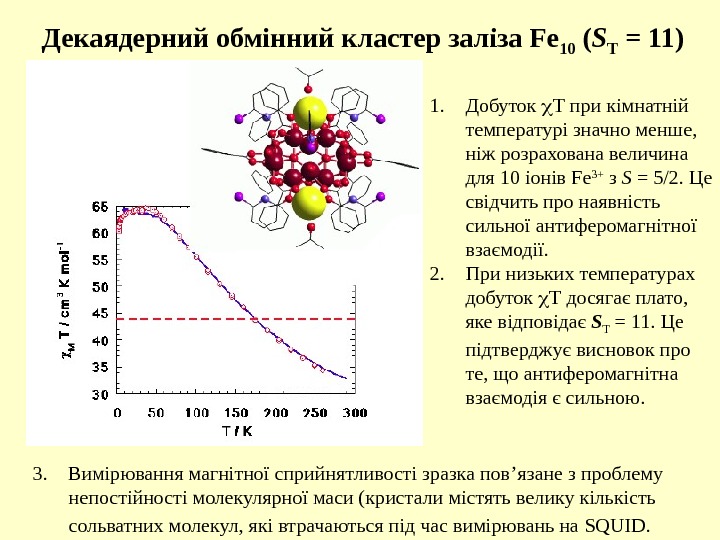
Декаядерний обмінний кластер заліза Fe 10 ( S T = 11) 1. Добуток Т при кімнатній температурі значно менше, ніж розрахована величина для 10 іонів Fe 3+ з S = 5/2. Це свідчить про наявність сильної антиферомагнітної взаємодії. 2. При низьких температурах добуток Т досягає плато, яке відповідає S T = 11. Це підтверджує висновок про те, що антиферомагнітна взаємодія є сильною. 3. Вимірювання магнітної сприйнятливості зразка пов ’ язане з проблему непостійності молекулярної маси (кристали містять велику кількість сольватних молекул, які втрачаються під час вимірювань на SQUID.

Нонаядерний обмінний кластер заліза Fe 9 Спроби віднесення спінових моментів і знаходження сумарного спіну виявляються безрезультатними (при цьому існує не одна, а декілька спінових невизначеностей.

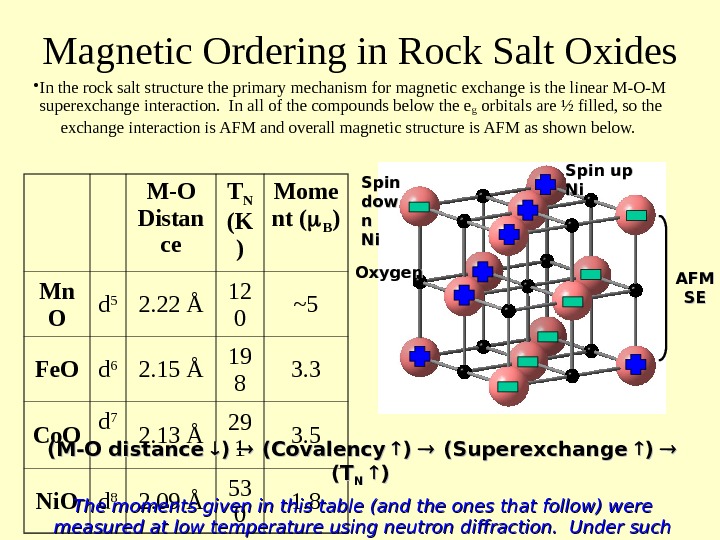
Magnetic Ordering in Rock Salt Oxides • In the rock salt structure the primary mechanism for magnetic exchange is the linear M-O-M superexchange interaction. In all of the compounds below the e g orbitals are ½ filled, so the exchange interaction is AFM and overall magnetic structure is AFM as shown below. M-O Distan ce T N (K ) Mome nt ( B ) Mn O d 5 2. 22 Å 12 0 ~5 Fe. O d 6 2. 15 Å 19 8 3. 3 Co. O d 7 2. 13 Å 29 1 3. 5 Ni. O d 8 2. 09 Å 53 0 1. 8(M-O distance ) ) (Covalency ) ) (Superexchange ) ) (T(T NN )) The moments given in this table (and the ones that follow) were measured at low temperature using neutron diffraction. Under such circumstances the moment should roughly be equal to the number of unpaired electrons. Spin up Ni. Spin dowdow n n Ni. Ni Oxygen AFMAFM SES

AFM Magnetic Ordering in Perovskites • The perovskite structure has even simpler magnetic interactions (in rock salt there is a competing interaction across the shared octahedral edge). Some magnetic data and the most common AFM structure for perovskite is shown below. The coloring of the magnetic structure is analogous to the crystal structure of Na. Cl. It is called the G-type magnetic structure. M-X Distanc e T N (K) Mome nt ( B ) La. Cr O 3 d 3 1. 97 Å 282 2. 8 Ca. Mn O 3 d 3 1. 90 Å 110 2. 6 La. Fe. O 3 d 5 1. 99 Å 750 4. 6 KNi. F 3 d 8 2. 00 Å 275 2. 2 Note that the superexchange that involves ½ filled e gg orbitals (La. Fe. O 33 ) is much stronger than the corresponding interaction of ½ filled t 2 g 2 g orbitals. Also upon going from oxide (La. Fe. O 33 ) to fluoride (KNi. F 33 ) the covalency decreases, which weakens the superexchange and lowers T NN. . Spin up Fe. Spin down Fe. Fe Oxygen AFMAFM SES

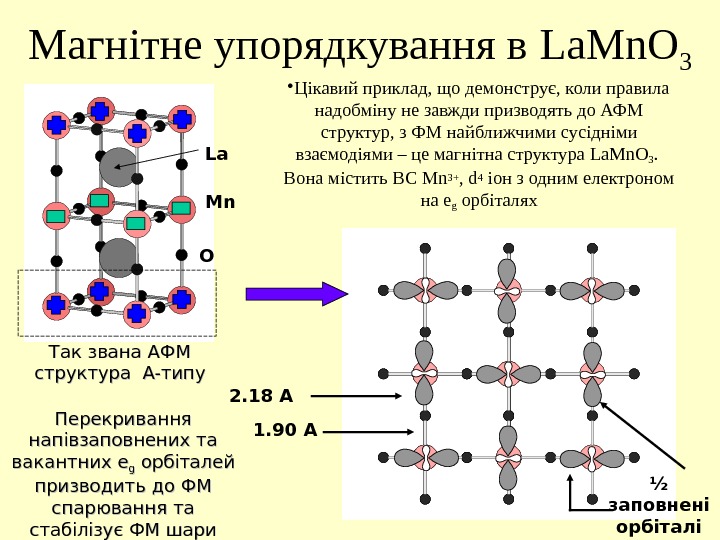
Магнітне упорядкування в La. Mn. O 3 • Цікавий приклад, що демонструє, коли правила надобміну не завжди призводять до АФМ структур , з ФМ найближчими сусідніми взаємодіями – це магнітна структура La. Mn. O 3. Вона містить ВС Mn 3+ , d 4 іон з одним електроном на e g орбіталях Mn. La O ½ заповнені орбіталі dz 2 типу Так звана АФМ структура A- A- типу 2. 18 A 1. 90 AПерекривання напівзаповнених та вакантних ee gg орбіталей призводить до ФМ спарювання та стабілізує ФМ шари

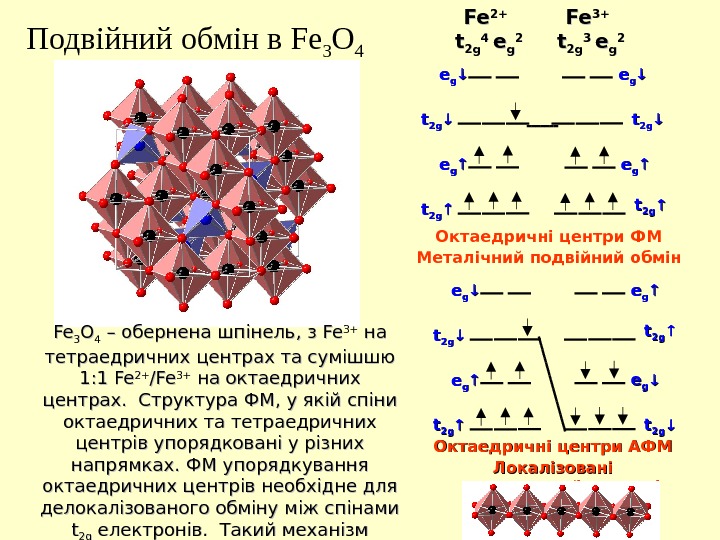
Подвійний обмін в Fe 3 O 4 ee g g tt 2 g 2 g ee g g tt 2 g 2 g Октаедричні центри ФМ Металічний подвійний обмін Октаедричні центри АФМ Локалізовані електрони // ізолюючіFe. Fe 2+2+ tt 2 g 2 g 4 4 ee gg 22 Fe. Fe 3+3+ tt 2 g 2 g 3 3 ee gg 22 Fe. Fe 33 OO 44 – обернена шпінель , , з з Fe. Fe 3+3+ на на тетраедричних центрах та сумішшю 1: 1 Fe 2+2+ /Fe/Fe 3+3+ на октаедричних центрах. . Структура ФМ , , у якій спіни октаедричних та тетраедричних центрів упорядковані у різних напрямках. . ФМ упорядкування октаедричних центрів необхідне для делокалізованого обміну між спінами tt 2 g 2 g електронів. . Такий механізм називається подвійним обміном. .

Summary • Magnetic Ordering in Solids – Diamagnetism : No unpaired e — – Paramagnetism : Unpaired e — , disordered and fluctuating – Ferromagnetism : All unpaired e — spins aligned parallel – Antiferromagnetism : Unpaired e — aligned antiparallel – Ferrimagnetism : Unpaired e — aligned antiparallel but don’t fully cancel out • Magnetic Superexchange – Unpaired electron spins couple through covalent interactions with intervening ligand – ½ filled metal orbital, AFM SE – ½ filled metal orbital – empty metal orbital, FM SE – Strength of superexchange interaction increases as covalency increases • Double Exchange – Spins on neighboring atoms must be aligned in a certain manner (usually ferromagnetically) in order to allow carrier delocalization – Magnetism and electrical transport are intimately linked

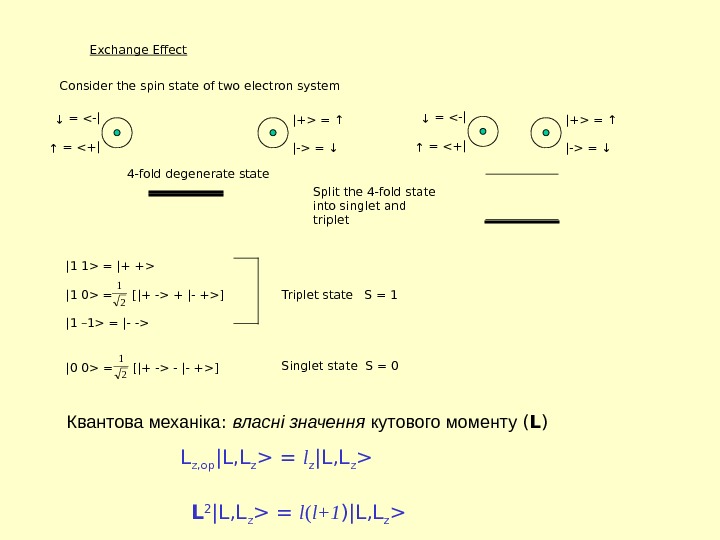
Exchange Effect Consider the spin state of two electron system|+> = ↓ |-> = ↑ |+> = ↑ |-> = ↓ 4 -fold degenerate state |+> = ↓ |-> = ↑ |+> = ↑ |-> = ↓ Split the 4 -fold state into singlet and triplet |1 1> = |+ +> |1 0> = [|+ -> + |- +>] |1 – 1> = |- -> Triplet state S = 1 |0 0> = [|+ -> — |- +>] Singlet state S = 0 2 1 Квантова механіка : власні значення кутового моменту ( L ) L z, op |L, L z > = l z |L, L z > L 2 |L, L z > = l ( l+1 )|L, L z >

Знаходження власних значень оператора спіну 4 3 )1 2 1 ( 2 12 2 2 1 SS 2121 2 2 23 2)( SSSSS 4 1 SS 2)11(1 S , 1 S 21 2 Для 4 3 SS 0 S , 0 S 21 2 Let’s set the spin Hamiltonian as 21)()3( 4 1 SStsts spin. EEEEH 00|) 43 )(()3( 41 00| ststsspin EEEEEH 11|) 41 )(()3( 41 11| ttstsspin EEEEEH 01|01| tspin EH 11|11| tspin EH H spin satisfies eigenstate and eigenvalue for the spin states. 21 SS JH spin ts EEJ ts EE for 21 SS ts EE 21 SS for

21 SS JH spin. Relative orientation of the two spins determines the energy states. Exchange energy * N ions of spin S i) (2 S+1) N -fold degenerate state for R inter >> 1 ii) Splitting of the degenerate state for R inter 1 Spin Hamiltonian for the splittings ji ji ijspin JH SS J ij = exchange coupling constant Heisenberg Hamiltonian

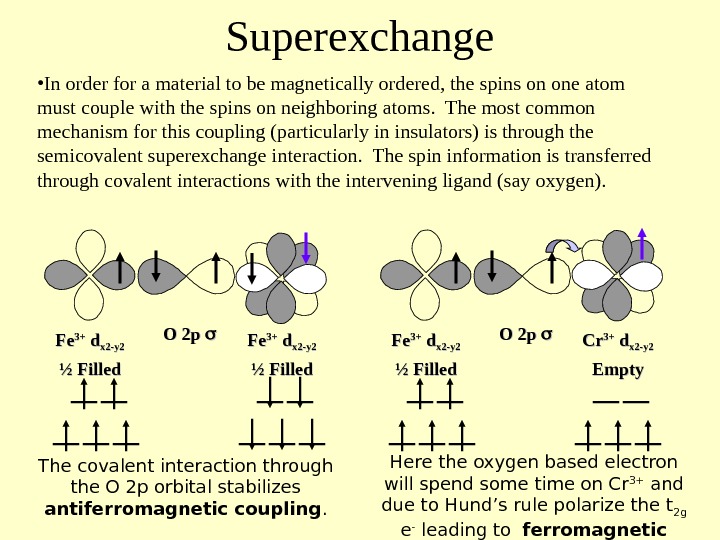
Superexchange • In order for a material to be magnetically ordered, the spins on one atom must couple with the spins on neighboring atoms. The most common mechanism for this coupling (particularly in insulators) is through the semicovalent superexchange interaction. The spin information is transferred through covalent interactions with the intervening ligand (say oxygen). Fe 3+3+ d d x 2 -y 2 ½ Filled Fe. Fe 3+3+ d d x 2 -y 2 ½ Filled. O 2 p The covalent interaction through the O 2 p orbital stabilizes antiferromagnetic coupling. Fe 3+3+ d d x 2 -y 2 ½ Filled Cr. Cr 3+3+ d d x 2 -y 2 Empty. O 2 p Here the oxygen based electron will spend some time on Cr 3+ and due to Hund’s rule polarize the t 2 g e — leading to ferromagnetic coupling.

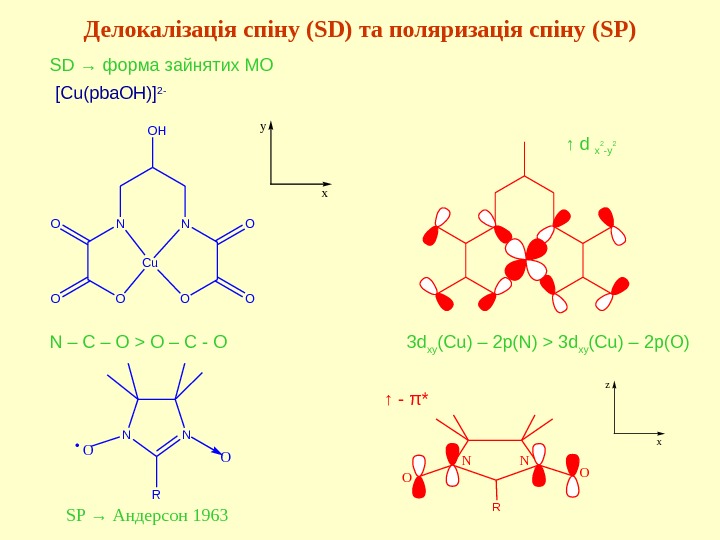
Делокалізація спіну ( SD) та поляризація спіну (SP) S D → форма зайнятих MO [Cu(pba. OH)] 2 — ↑ d x 2 -y 2 N – C – O > O – C — O 3 d xy (Cu) – 2 p(N) > 3 d xy (Cu) – 2 p(O) SP → Андерсон 1963 N O H N O OO C u y x N N R O. O ROO NN z x↑ — π *

CBA CA CBA 2 21 3 21 Eijrji ijsp /)()(/1)()( )()1( 2321 2312112/12 CH CH 2. A B C зв ’ язуючі незв ’ язуючі антизв ’ язуючі Основний стан 211 ↑ — 2 ( делокалізований на A та C) Monoexited state 231 where

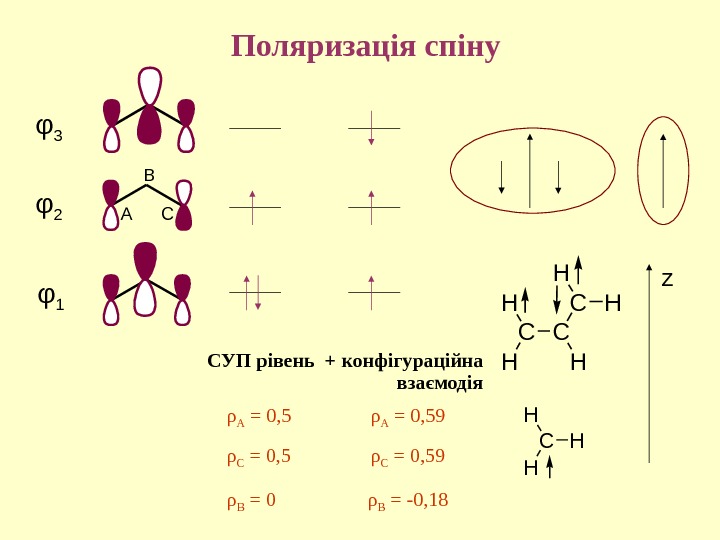
Поляризація спіну СУП р івень + конфігураційна взаємодія ρ A = 0, 59 ρ C = 0, 59 ρ B = 0 ρ B = -0, 18 CC C H H H CH H H zφ 2 φ 3 φ