Oblivious Signature-Based Envelope Ninghui Li Stanford University Wenliang

Oblivious Signature-Based Envelope Ninghui Li, Stanford University Wenliang (Kevin) Du, Syracuse University Dan Boneh, Stanford University

Motivation Alice Bob I have an message P to report, but I want to make sure you are CIA. Please show me your CIA certificate. I won’t show my CIA certificate to you, just give me the message. ? ? ?

Outline of This Presentation Introduce the Oblivious Signature. Based Envelope (OSBE) concept. n An OSBE scheme for RSA signatures. n OSBE using Identity Based Encryption (IBE). n Summary and Future Work. n

Public Key Certificate (an example) n Bob’s CIA certificate: PK: the CIA’s public key. n M: “Bob is with CIA” n = Sig. PK(M): signature on M (certificate). n n The secret part is

Oblivious Signature-Based Envelope (OSBE) Receiver Sender Message P • Receiver can open the envelope if and only if he/she has the certificate. • Sender cannot know whether the receiver has the certificate.

OSBE Definition n Setup n n n n PK: the Certificate Authority’s public key. M: content of the certificate. = Sig. PK(M): signature on M (certificate). S: Sender of message P (P is given to S only). R 1: Receiver with . R 2: Receiver without . PK and M are given to all three parties.

OSBE Definition (cont’d) n Interaction One of R 1 and R 2 is chosen as R, without S knowing which one. n S and R run an interactive protocol. n n Open R outputs P if and only if R = R 1. n Note: R 1 has the certificate, R 2 doesn’t. n

Security Requirements n Sound: R 1 can output P with overwhelming probability. n Oblivious: S does not learn whether it is communicating with R 1 or R 2. Semantically secure against the receiver: R 2 learns nothing about P. n

Outline of This Presentation Introduce the Oblivious Signature. Based Envelope (OSBE) concept. n An OSBE scheme for RSA signatures. n OSBE using Identity Based Encryption (IBE). n Summary and Future Work. n

An OSBE Scheme for RSA n RSA Signatures: (e, n): public key PK. n d: private key. n h = hash(M): hash value of M. n = Sig. PK(M) = hd (mod n): signature. n (hd)e = (he)d = h (mod n). n

RSA-OSBE Scheme: Setup n Setup: Everybody knows h, M, (e, n) n Sender S knows: P n Receiver R 1 knows: = (hd mod n) n

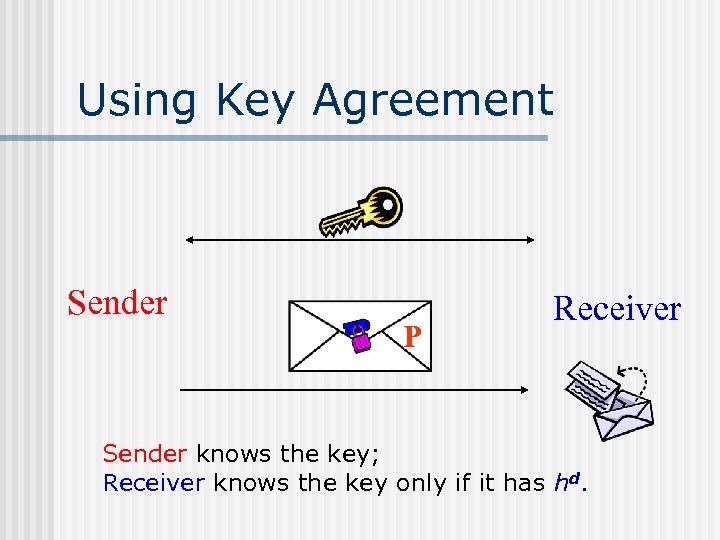
Using Key Agreement Sender P Receiver Sender knows the key; Receiver knows the key only if it has hd.

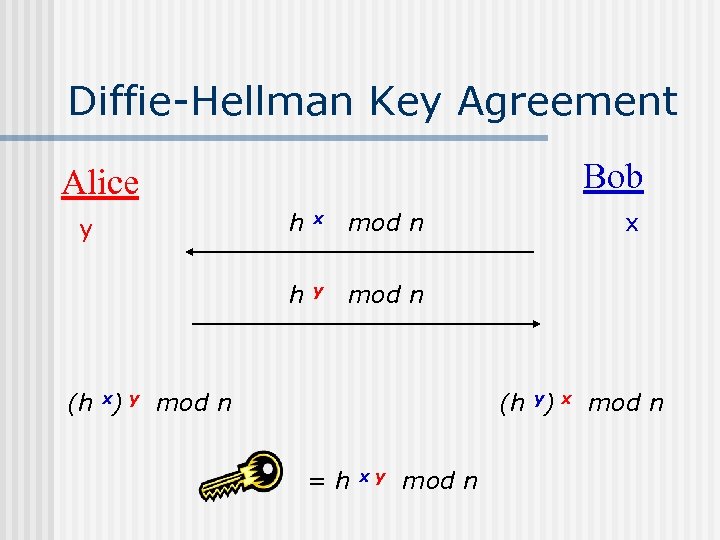
Diffie-Hellman Key Agreement Bob Alice h x mod n h y y mod n (h x) y mod n x (h y) x mod n =h xy mod n

Transforming Diffie-Hellman S y R 1 = h d · h x mod n =h e y = (h d+x) e y = h edy· h exy = h y · h exy r = ey x mod n r ‘ = (h e y) x e y /h y = h e x y r = r’ if and only if Receiver knows h d

Properties n Theorem 1: RSA-OSBE is sound (r = r’) n Theorem 2: RSA-OSBE is oblivious = hd+x n. R 2: = hx’ n R 1 : n{hd+x | x random} and {hx’ | x’ random} are statistically indistinguishable. Theorem 3: RSA-OSBE is semantically secure against the receiver, i. e, R 2 cannot learn r. n

Proof of Theorem 3 (Approach) n Approach n We show that, if there exists an adversary receiver R (who does know hd) that can break RSA-OSBE • i. e. , R can learn r by interacting with S, n Then we can build an attacker that can generate hd. i. e. , we can use R to break RSA signatures

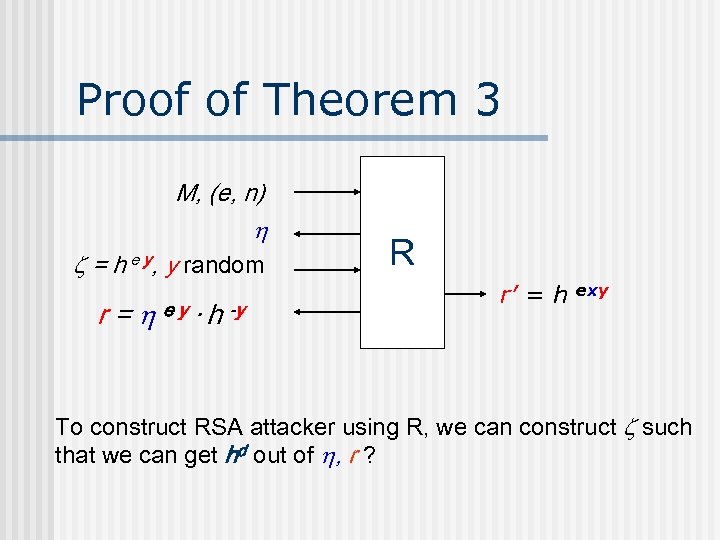
Proof of Theorem 3 M, (e, n) = h e y, y random r = e y · h -y R r’ = h exy To construct RSA attacker using R, we can construct such that we can get hd out of , r ?

Proof of Theorem 3 (cont’d) = h ey r = e y · h -y R RSA Attacker randomly generates k, constructs = h 1+ ek = h e (d+k) Let y = d+k, then = h e y R outputs r = e y · h -y = e(d+k) · h-(d+k) = 1+ek · h-d · h-k, Attacker knows

Outline of This Presentation Introduce the Oblivious Signature. Based Envelope (OSBE) concept. n An OSBE scheme for RSA signatures. n OSBE using Identity Based Encryption (IBE). n Summary and Future Work. n

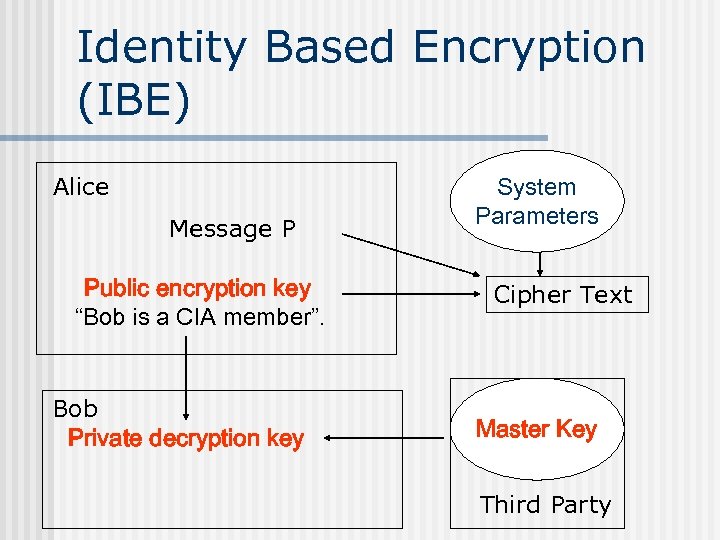
Identity Based Encryption (IBE) Alice Message P Public encryption key “Bob is a CIA member”. Bob Private decryption key System Parameters Cipher Text Master Key Third Party

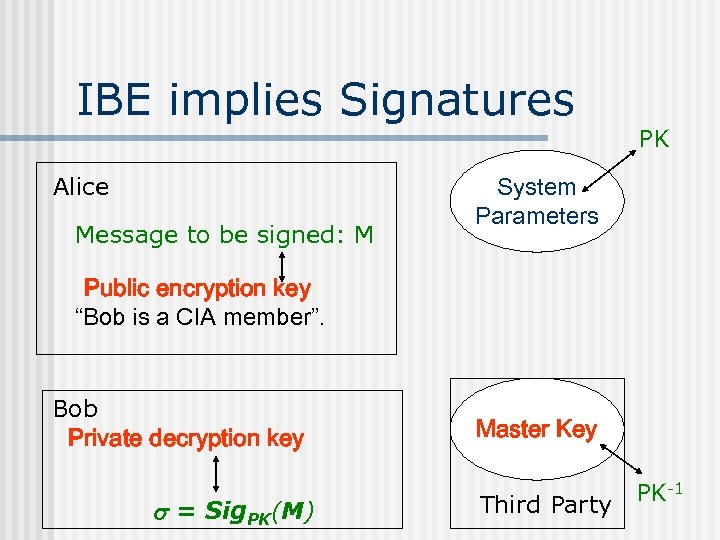
IBE implies Signatures Alice Message to be signed: M PK System Parameters Public encryption key “Bob is a CIA member”. Bob Private decryption key = Sig. PK(M) Master Key PK-1 Third Party

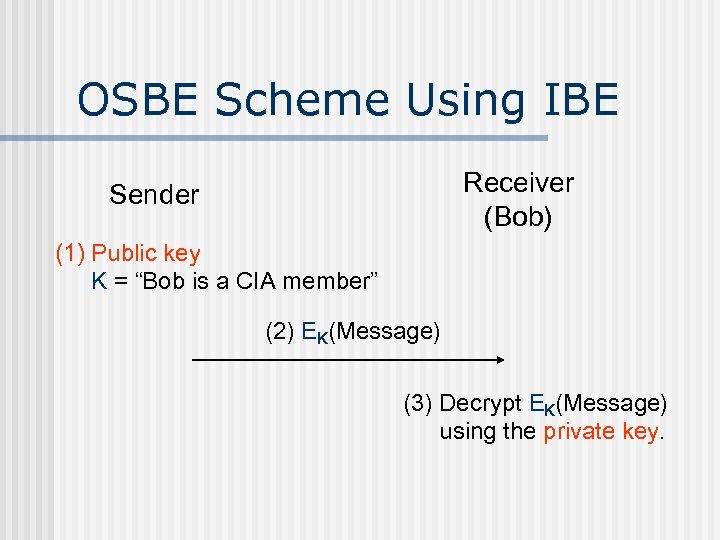
OSBE Scheme Using IBE Receiver (Bob) Sender (1) Public key K = “Bob is a CIA member” (2) EK(Message) (3) Decrypt EK(Message) using the private key.

Comparisons IBE-OSBE is one round; RSA-OSBE needs two rounds. n RSA-OSBE can be used on existing Public Key Infrastructure. n

Summary and Future Work OSBE concept n RSA-OSBE scheme and IBE-OSBE scheme n Future Work: n n Find OSBE scheme for DSA signatures.