174ebc76f0ea32fadecf4979ec6ad135.ppt
- Количество слайдов: 11

Objectives Ø The objectives of the workshop are to stimulate discussions around the use of 3 D (and probably 4 D = 3 D+time) realistic modeling of canopy structure to be used in remote sensing applications. Ø On what basis is it possible to derive simpler RT representations for operational applications?

Stochastic Radiative Transfer for Remote Sensing of Vegetation Y. Knyazikhin 1, D. Huang 1, N. Shabanov 1, W. Yang 1, M. Rautiainen 2, R. B. Myneni 1 1 Department 2 Department of Geography, Boston University of Forest Ecology, University of Helsinki jknjazi@bu. edu WORKSHOP ON THE USE OF 3 D REALISTIC CANOPY ARCHITECTURE MODELING FOR REMOTE SENSING APPLICATIONS Avignon, France, March-9, 2005

INTERPRETATION OF SATELLITE DATA • Satellite-borne sensors measure mean intensities of canopyleaving radiance averaged over the three-dimensional canopy radiation field • Three-dimensional radiation models can simulate 3 D radiation field. However, they require 3 D input and are time consuming • Operational data processing requires fast retrieval algorithms. One – dimensional model is the desirable option. Problem: To develop a radiative transfer approach for modeling the radiation regime of natural vegetation which is 1. as realistic as 3 D model 2. as simple as 1 D model
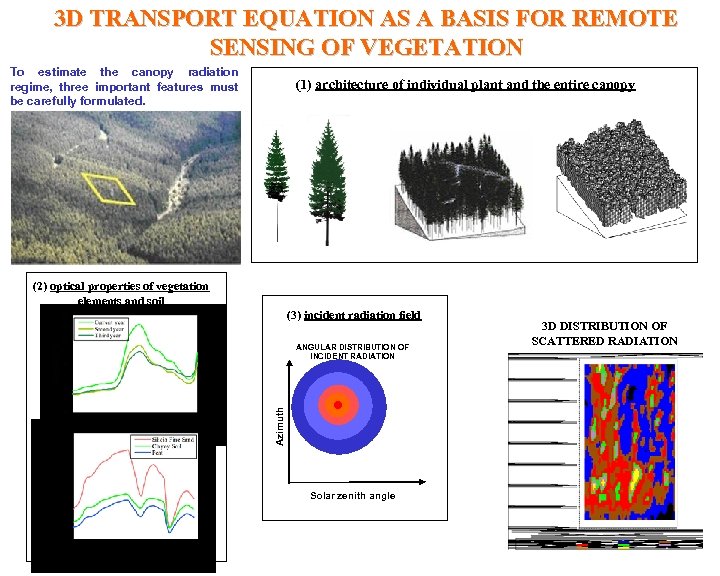
3 D TRANSPORT EQUATION AS A BASIS FOR REMOTE SENSING OF VEGETATION To estimate the canopy radiation regime, three important features must be carefully formulated. (1) architecture of individual plant and the entire canopy (2) optical properties of vegetation elements and soil (3) incident radiation field Azimuth ANGULAR DISTRIBUTION OF INCIDENT RADIATION Solar zenith angle 3 D DISTRIBUTION OF SCATTERED RADIATION
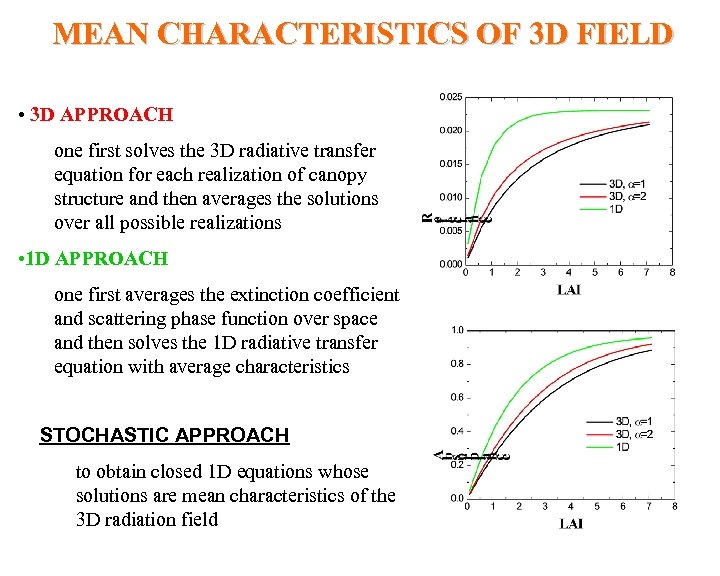
MEAN CHARACTERISTICS OF 3 D FIELD • 3 D APPROACH one first solves the 3 D radiative transfer equation for each realization of canopy structure and then averages the solutions over all possible realizations • 1 D APPROACH one first averages the extinction coefficient and scattering phase function over space and then solves the 1 D radiative transfer equation with average characteristics STOCHASTIC APPROACH to obtain closed 1 D equations whose solutions are mean characteristics of the 3 D radiation field

HISTORY “The problem of obtaining closed equations for probabilistic characteristics of the radiation field was first formulated and solved by G. M. Vainikko (1973) where the equations for the mean radiance … were derived through spatial averaging of the stochastic transfer equation in the model of broken cloudiness, sampling realization of which cannot be constructed. The method of G. M. Vainikko has limited efficiency. …. These disadvantages were avoided in later papers…. ” (Titov, G. , Statistical description of radiation transfer in clouds, J. Atmos. Sci. , 47, p. 29, 1990) Pomraning, G. C. (1991). Linear kinetic theory and particle transport in stochastic mixtures. World Scientific Publishing Co. Pte. Ltd. , Singapore. Shabanov, N. V. , Y. Knyazikhin, F. Baret, and R. B. Myneni, Stochastic modeling of radiation regime in discontinuous vegetation canopy, Remote Sens. Environ, 74, 125 -144, 2000. Vainikko, G. (1973). Transfer approach to the mean intensity of radiation in noncontinuous clouds. Trudy MGK SSSR, Meteorological Investigations, 21, 28– 37. George Titov and Jerry Pomraning. From A. Marshak and A. Davis (Eds), Three. Dimensional Radiative Transfer in Cloudy Atmospheres. Springer Verlag.
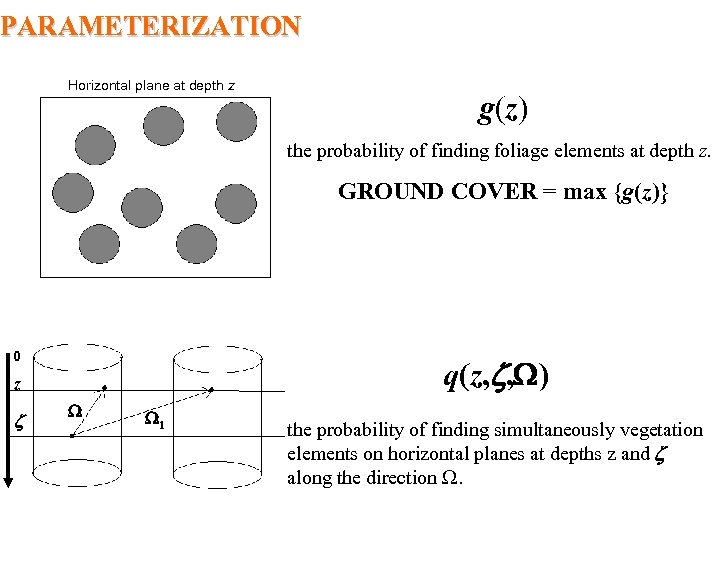
PARAMETERIZATION Horizontal plane at depth z g(z) the probability of finding foliage elements at depth z. GROUND COVER = max {g(z)} 0 q(z, , ) z 1 the probability of finding simultaneously vegetation elements on horizontal planes at depths z and along the direction .
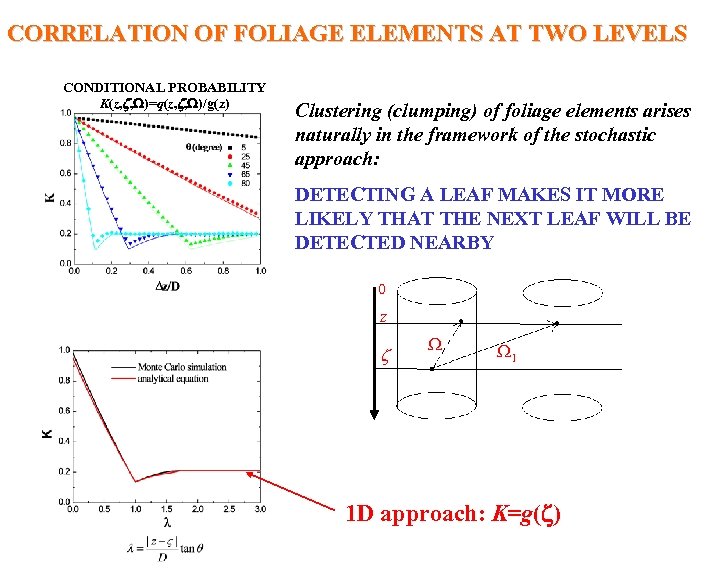
CORRELATION OF FOLIAGE ELEMENTS AT TWO LEVELS CONDITIONAL PROBABILITY K(z, , )=q(z, , )/g(z) Clustering (clumping) of foliage elements arises naturally in the framework of the stochastic approach: DETECTING A LEAF MAKES IT MORE LIKELY THAT THE NEXT LEAF WILL BE DETECTED NEARBY 0 z 1 1 D approach: K=g( )
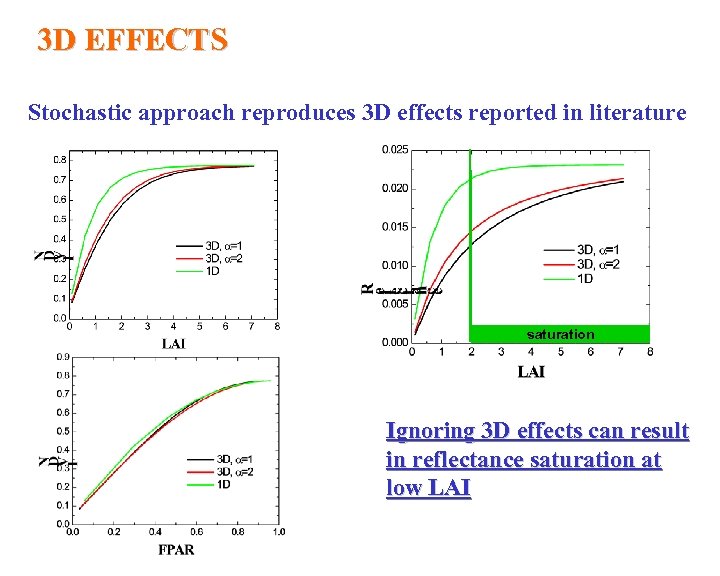
3 D EFFECTS Stochastic approach reproduces 3 D effects reported in literature saturation Ignoring 3 D effects can result in reflectance saturation at low LAI
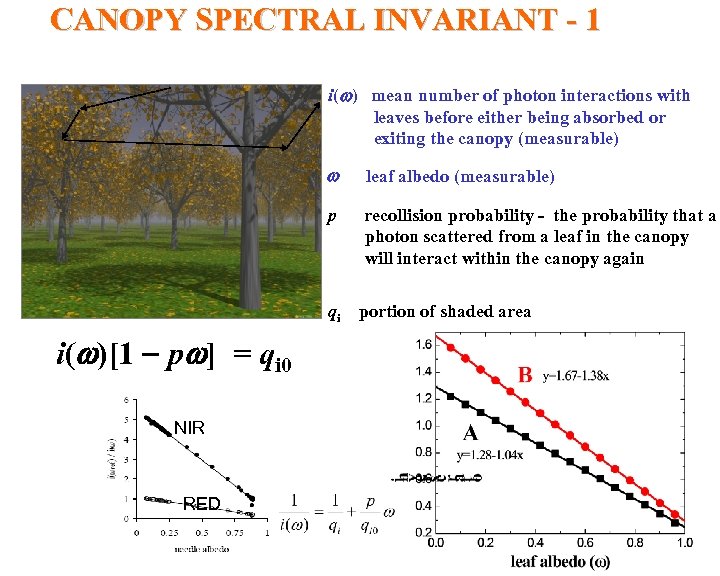
CANOPY SPECTRAL INVARIANT - 1 i(w) mean number of photon interactions with leaves before either being absorbed or exiting the canopy (measurable) w leaf albedo (measurable) p recollision probability - the probability that a photon scattered from a leaf in the canopy will interact within the canopy again qi portion of shaded area i(w)[1 pw] = qi 0 NIR RED

CONCLUSIONS Ø On what basis is it possible to derive simpler RT representations for operational applications? Stochastic Transfer Equation because q Its solution coincides exactly with what satellite-borne sensors measure; that is, the mean field emanating from the smallest area to be resolved, from a pixel q It reproduces 3 D effects q It provides a powerful tool to parameterize 3 D effects q It is as simple as 1 D Radiative Transfer Equation Ø The objectives of the workshop are to stimulate discussions around the use of 3 D (and probably 4 D = 3 D+time) realistic modeling of canopy structure to be used in remote sensing applications. Realistic models of canopy structure are required to derive and parameterize the “q-function” which describes the correlation of foliage elements in vegetation canopies
174ebc76f0ea32fadecf4979ec6ad135.ppt