de2dfc6e158c1ade7b847a2fea1f51a6.ppt
- Количество слайдов: 62

Objective • Fault Detection capturing the fault and estimating the time of fault occurrence • Fault Isolation determination of the location of the fault in the system • Fault Identification estimation of the size and the type of the fault Electrical & Computer Engineering Department University of Patras 1
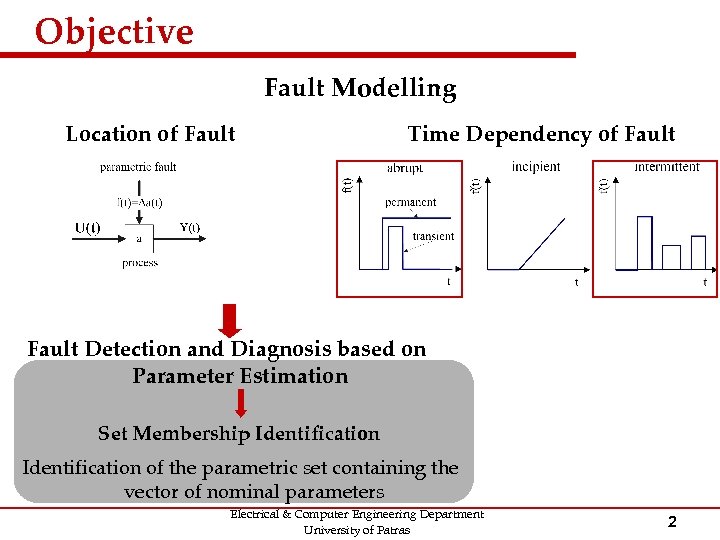
Objective Fault Modelling Location of Fault Time Dependency of Fault Detection and Diagnosis based on Parameter Estimation Set Membership Identification of the parametric set containing the vector of nominal parameters Electrical & Computer Engineering Department University of Patras 2

Presentation Outline • Set Membership Identification (SMI) – Orthotope-based Set Membership Identification – Ellipsoid-based Set Membership Identification • Fault Detection and Diagnosis (FDD) based on SMI – Fault Detection based on SMI – Fault Isolation based on SMI – Fault Identification based on SMI Electrical & Computer Engineering Department University of Patras 3

Set Membership Identification Assumptions • Linearly parametrizable model • Observed data • Unknown but bounded noise Electrical & Computer Engineering Department University of Patras a priori known worst case bound 4

Set Membership Identification Data-hyperspace Configuration Noiseless Regression Vector • At every time instant, the nominal parameter vector resides in the data-hyperspace: hyperspace between two parallel hyperplanes hyperstrip Electrical & Computer Engineering Department University of Patras 5
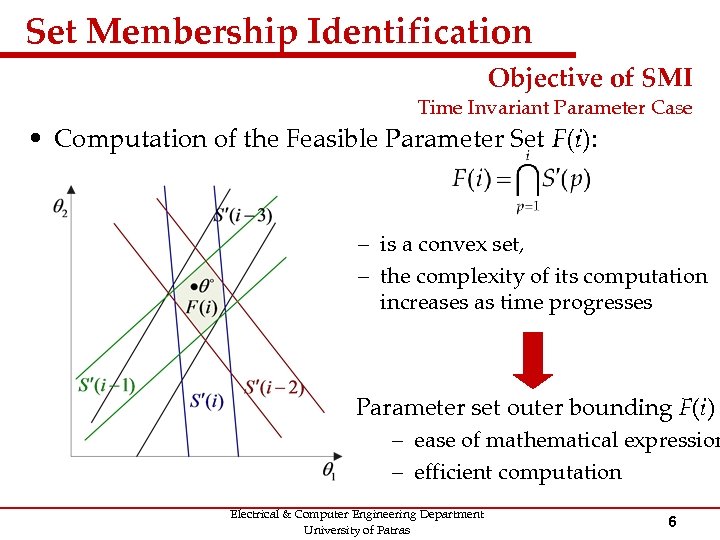
Set Membership Identification Objective of SMI Time Invariant Parameter Case • Computation of the Feasible Parameter Set F(i): – is a convex set, – the complexity of its computation increases as time progresses Parameter set outer bounding F(i) – ease of mathematical expression – efficient computation Electrical & Computer Engineering Department University of Patras 6

Set Membership Identification Orthotope-based SMI Time Invariant Parameter Case • Outer Bounding Orthotope Ω(i): Projection of orthotope: Electrical & Computer Engineering Department University of Patras 7

Set Membership Identification Orthotope-based SMI • Recursive Computation of Ω(i): Time Invariant Parameter Case Optimal Solutions of a Linear Programming Problem with n variables and 2(n+1) constraints Electrical & Computer Engineering Department University of Patras 8

Set Membership Identification Ellipsoid-based SMI Time Invariant Parameter Case • Outer Bounding Ellipsoid Θ(i): Electrical & Computer Engineering Department University of Patras 9

Set Membership Identification Ellipsoid-based SMI • Support-Orthotope of Ellipsoid Time Invariant Parameter Case : defined by the intersection of the support hyperplanes of ellipsoid, which are parallel to the coordinate axes Electrical & Computer Engineering Department University of Patras 10

Set Membership Identification Ellipsoid-based SMI Time Invariant Parameter Case • Recursive Computation of Θ(i): Electrical & Computer Engineering Department University of Patras 11

Set Membership Identification Assumptions • Linearly parametrizable model Noisy Regression Vector • Observed data • Unknown but bounded noise a priori known worst case bounds Electrical & Computer Engineering Department University of Patras 12

Set Membership Identification Data Hyperspace Configurations Noisy Regression Vector • Data-hyperstrip Electrical & Computer Engineering Department University of Patras 13

Set Membership Identification Data Hyperspace Configurations • Data-hypersector Noisy Regression Vector Electrical & Computer Engineering Department University of Patras 14

Set Membership Identification Orthotope-based SMI Noisy Regression Vector • Recursive Computation of Ω(i) using the data-hyperstrip • Recursive Computation of Ω(i) using the data-hypersector Electrical & Computer Engineering Department University of Patras 15

Set Membership Identification Ellipsoid-based SMI Noisy Regression Vector • Recursive Computation of Θ(i) using the data-hyperstrip • Recursive Computation of Θ(i) using the data-hypersector Electrical & Computer Engineering Department University of Patras 16

Set Membership Identification Assumptions • Time varying linearly parametrizable model • : corresponds to slow rate parameter perturbations with a priori known worst case bounds Electrical & Computer Engineering Department University of Patras 17

Set Membership Identification Orthotope-based SMI Time Varying Parameter Case Electrical & Computer Engineering Department University of Patras 18

Set Membership Identification Ellipsoid-based SMI Time Varying Parameter Case Electrical & Computer Engineering Department University of Patras 19

Fault Detection & Diagnosis Assumptions • Jump, Linearly Parametrizable Model describing multiple abrupt parametric faults Electrical & Computer Engineering Department University of Patras 20

Fault Detection & Diagnosis Assumptions • Jump Parameter Case • Safe Operation Bounds Electrical & Computer Engineering Department University of Patras 21

Fault Detection & Diagnosis Fault Detection Time Invariant Parameter Case • 1 st Fault Detection Criterion A fault is detected when an inconsistency between the measurement data and the inherent assumptions denotes the time instant of fault detection and is the detection-index The time instances of fault detection should be identical to the fault-occurrence instants or close to them, Electrical & Computer Engineering Department University of Patras 22
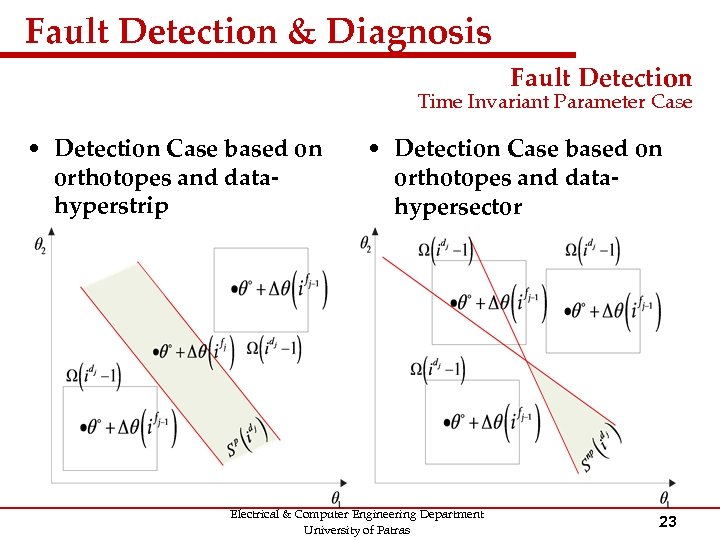
Fault Detection & Diagnosis Fault Detection Time Invariant Parameter Case • Detection Case based on orthotopes and datahyperstrip • Detection Case based on orthotopes and datahypersector Electrical & Computer Engineering Department University of Patras 23

Fault Detection & Diagnosis Fault Detection Time Invariant Parameter Case • Intersection of Support Orthotopes – At every time instant the parameter vector is contained within the computed ellipsoid and its support orthotope, since – Rather than relying solely on the ellipsoidal methods (e. g. OVE) in which, the intersection of support orthotopes is used as another fault detection criterion defined as Electrical & Computer Engineering Department University of Patras 24
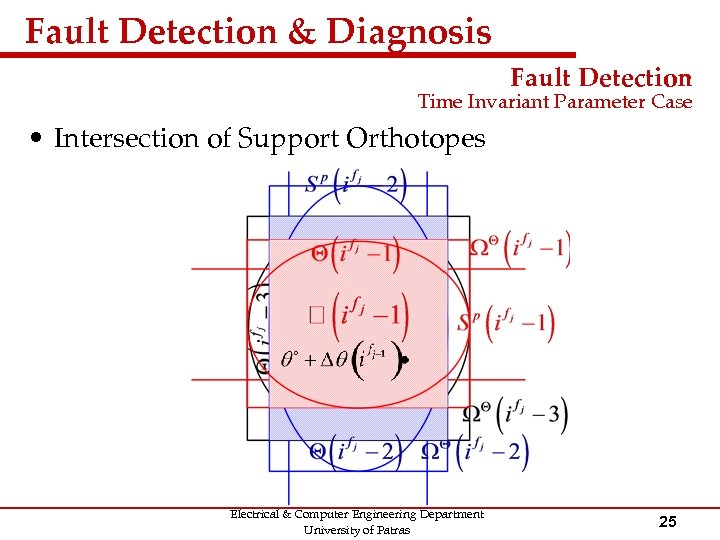
Fault Detection & Diagnosis Fault Detection Time Invariant Parameter Case • Intersection of Support Orthotopes Electrical & Computer Engineering Department University of Patras 25
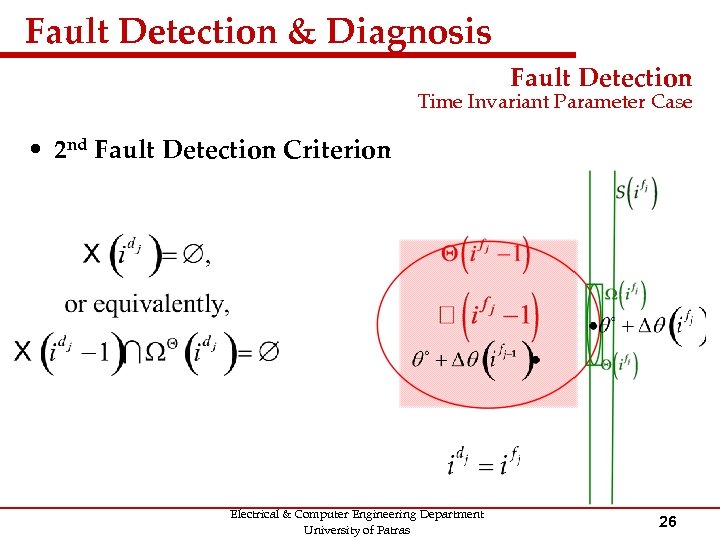
Fault Detection & Diagnosis Fault Detection Time Invariant Parameter Case • 2 nd Fault Detection Criterion Electrical & Computer Engineering Department University of Patras 26

Fault Detection & Diagnosis Fault Diagnosis Time Invariant Parameter Case • Resetting Procedure based on Orthotopes Electrical & Computer Engineering Department University of Patras 27

Fault Detection & Diagnosis Fault Diagnosis Time Invariant Parameter Case • Resetting Procedure based on Ellipsoids Electrical & Computer Engineering Department University of Patras 28

Fault Detection & Diagnosis Fault Diagnosis Time Invariant Parameter Case • Resetting Procedure based on the Intersection of Support Orthotopes Electrical & Computer Engineering Department University of Patras 29

Fault Detection & Diagnosis Fault Diagnosis • Resetting the Data-Hyperspace Time Invariant Parameter Case Electrical & Computer Engineering Department University of Patras 30

Fault Detection & Diagnosis Fault Diagnosis Time Invariant Parameter Case • Fault Isolation – Faulty Components – Non-Faulty Components Electrical & Computer Engineering Department University of Patras 31

Fault Detection & Diagnosis Fault Diagnosis Time Invariant Parameter Case • Fault Identification – The most likely estimate of parameter deviation of the faulty components is computed as: Electrical & Computer Engineering Department University of Patras 32

Fault Detection & Diagnosis Assumptions Time Varying Parameter Case • Jump linearly parametrizable model: • Safe Operation Parameter Bounds Electrical & Computer Engineering Department University of Patras 33

Fault Detection & Diagnosis Time Varying Parameter Case • The Fault Detection mechanism relies on the 1 st Fault Detection Criterion, modified as: • The Resetting Procedure is applied in the augmented parametric set Electrical & Computer Engineering Department University of Patras 34

Fault Detection & Diagnosis Time Varying Parameter Case • Fault Isolation – Computation of Parameter Set within which the nominal parameter vector would have reside, if no fault has occurred Electrical & Computer Engineering Department University of Patras 35
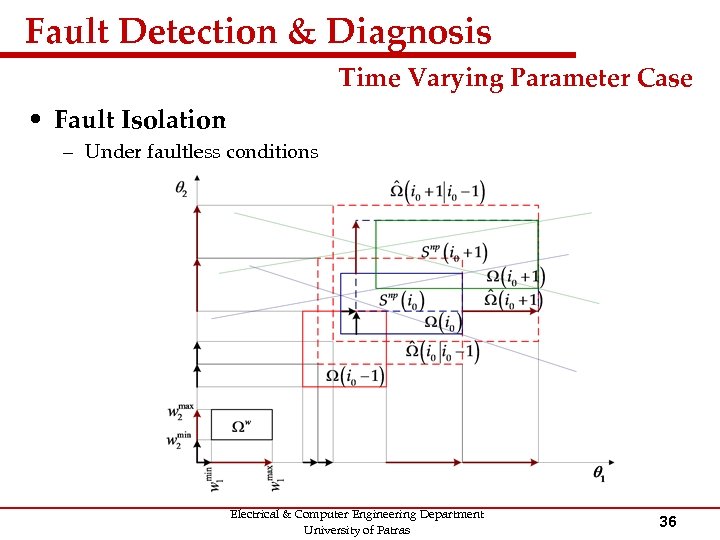
Fault Detection & Diagnosis Time Varying Parameter Case • Fault Isolation – Under faultless conditions Electrical & Computer Engineering Department University of Patras 36
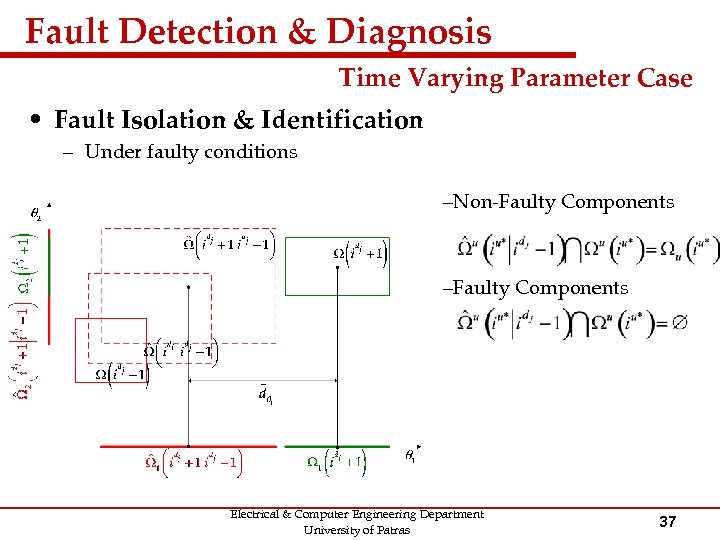
Fault Detection & Diagnosis Time Varying Parameter Case • Fault Isolation & Identification – Under faulty conditions –Non-Faulty Components –Faulty Components Electrical & Computer Engineering Department University of Patras 37
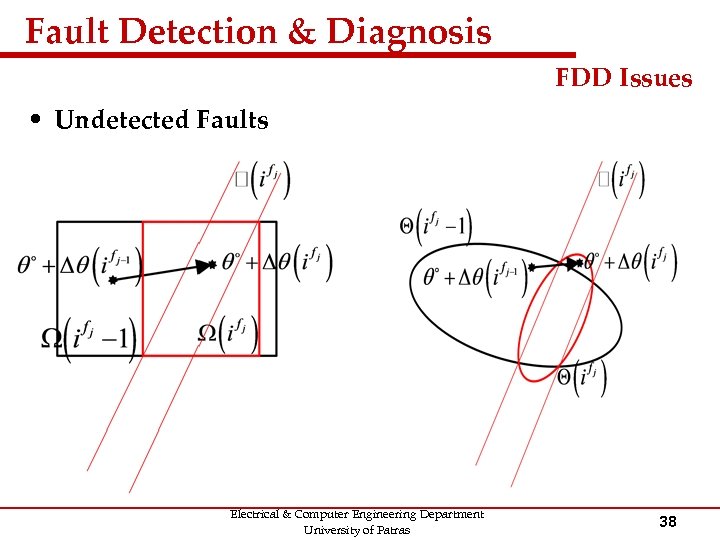
Fault Detection & Diagnosis FDD Issues • Undetected Faults Electrical & Computer Engineering Department University of Patras 38

Fault Detection & Diagnosis FDD Issues • Incorrect time instant of fault detection – The time instant of fault detection can be different than the time of fault occurrence, – If then our assumption of a jump system for which the parameter vector remains constant for at least Lsamples after the occurrence of a fault contradicts our findings Electrical & Computer Engineering Department University of Patras 39

Fault Detection & Diagnosis • Backward-in-Time Procedure Electrical & Computer Engineering Department University of Patras FDD Issues 40
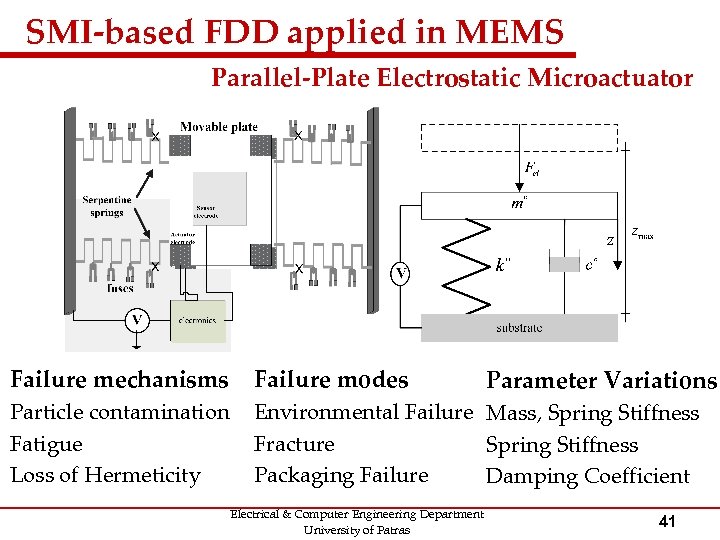
SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator Failure mechanisms Failure modes Particle contamination Fatigue Loss of Hermeticity Environmental Failure Mass, Spring Stiffness Fracture Spring Stiffness Packaging Failure Damping Coefficient Electrical & Computer Engineering Department University of Patras Parameter Variations 41

SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator • System Dynamics: • Time Invariant Linearly Parametrizable Model: • Observed Measurement Data: Electrical & Computer Engineering Department University of Patras 42
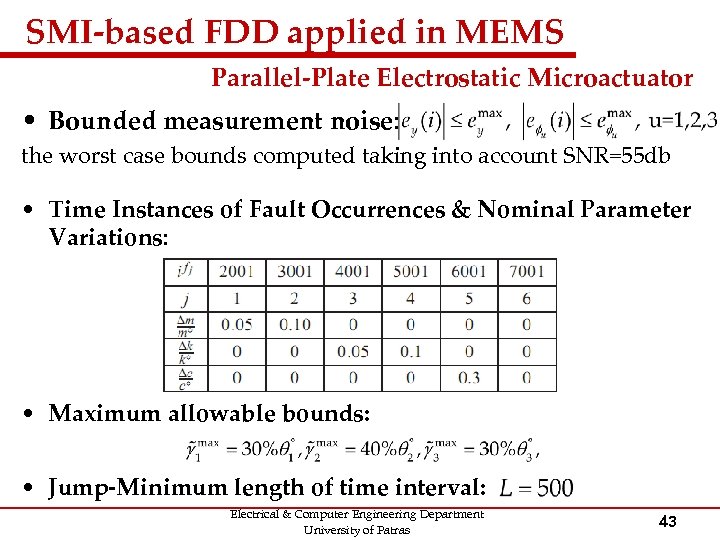
SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator • Bounded measurement noise: the worst case bounds computed taking into account SNR=55 db • Time Instances of Fault Occurrences & Nominal Parameter Variations: • Maximum allowable bounds: • Jump-Minimum length of time interval: Electrical & Computer Engineering Department University of Patras 43

SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator • Simulation Study Objective: Capture and diagnose the faults applying the following FDD schemes – (A) FDD based on Orthotopic SMI using data-hyperstrips – (B) FDD based on Orthotopic SMI using data-hypersectors – (C) FDD based on Ellipsoidal SMI using data-hyperstrips – (D) FDD based on Ellipsoidal SMI using data-hypersectors • Time Instances of Fault Occurrence and Detection Electrical & Computer Engineering Department University of Patras 44
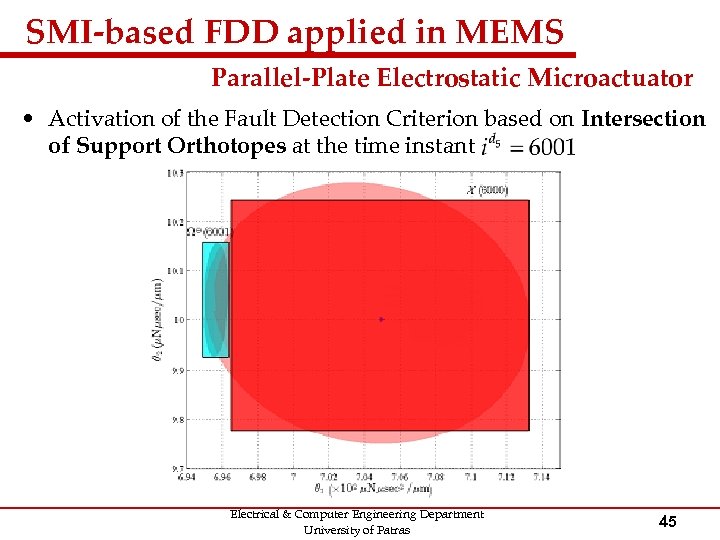
SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator • Activation of the Fault Detection Criterion based on Intersection of Support Orthotopes at the time instant Electrical & Computer Engineering Department University of Patras 45
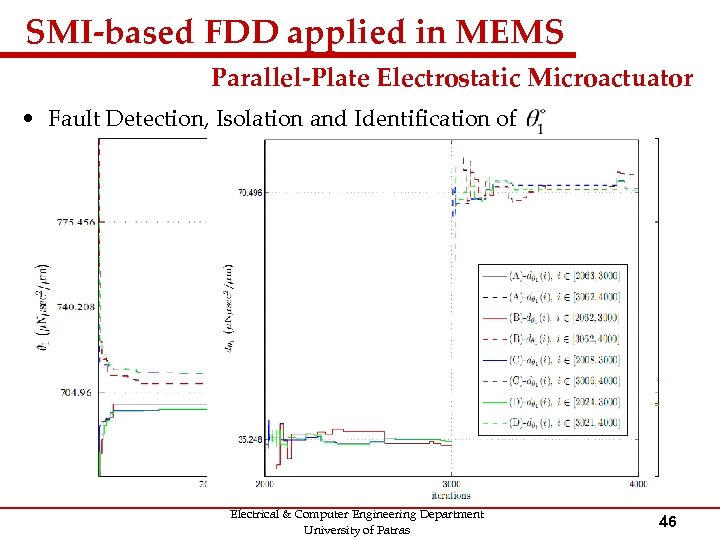
SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator • Fault Detection, Isolation and Identification of Electrical & Computer Engineering Department University of Patras 46
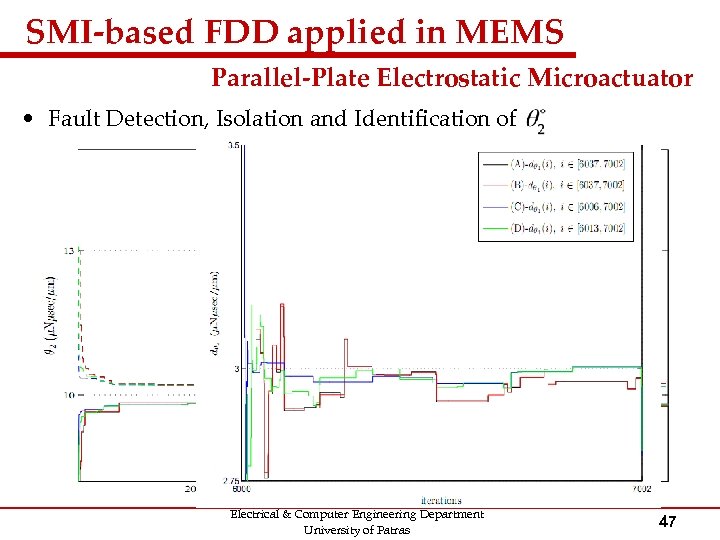
SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator • Fault Detection, Isolation and Identification of Electrical & Computer Engineering Department University of Patras 47
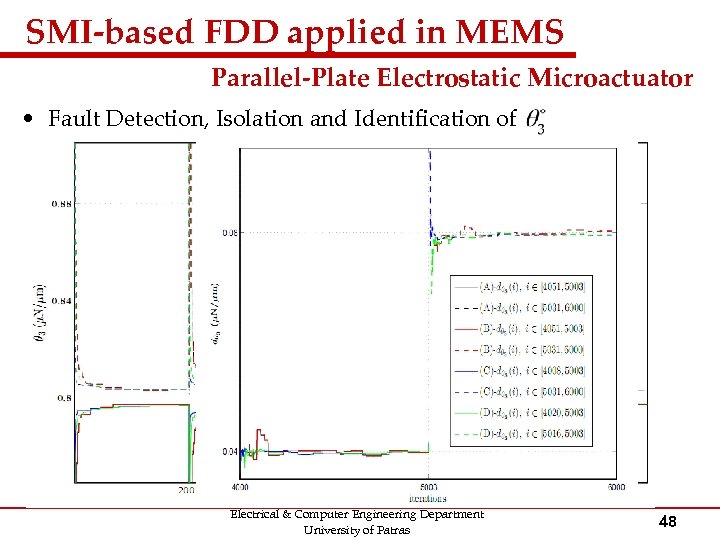
SMI-based FDD applied in MEMS Parallel-Plate Electrostatic Microactuator • Fault Detection, Isolation and Identification of Electrical & Computer Engineering Department University of Patras 48
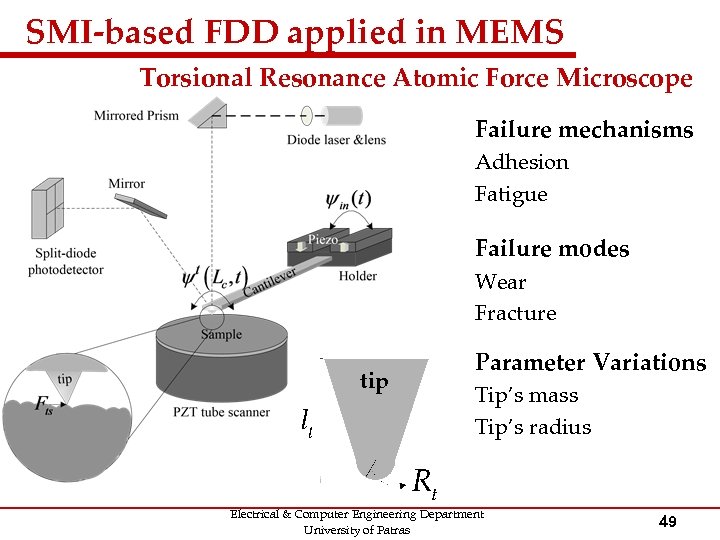
SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope Failure mechanisms Adhesion Fatigue Failure modes Wear Fracture tip Parameter Variations Tip’s mass Tip’s radius Electrical & Computer Engineering Department University of Patras 49

SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • System Dynamics: • • The TR-AFM is working in the repulsive regime • Due to the roughness surface, slowly are assumed to vary Electrical & Computer Engineering Department University of Patras 50

SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • Time Varying Linearly Parametrizable Model: • Observed Measurement Data Electrical & Computer Engineering Department University of Patras 51

SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • Slowly varying lateral stiffness and tip’s radius • Safe Operation Parameter Bounds: • Nominal Parameter Variations (Tip’s fractures) : Electrical & Computer Engineering Department University of Patras 52

SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • Simulation Study Objective: Capture and diagnose the faults applying the following FDD schemes – (A) FDD based on Orthotopic SMI using data-hyperstrips – (B) FDD based on Orthotopic SMI using data-hypersectors – (C) FDD based on Ellipsoidal SMI using data-hyperstrips – (D) FDD based on Ellipsoidal SMI using data-hypersectors • Time Instances of Fault Occurrence and Detection Electrical & Computer Engineering Department University of Patras 53
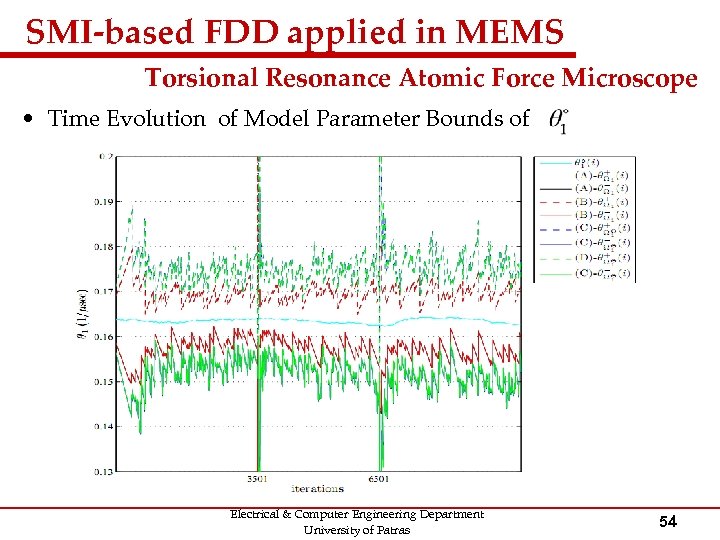
SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • Time Evolution of Model Parameter Bounds of Electrical & Computer Engineering Department University of Patras 54
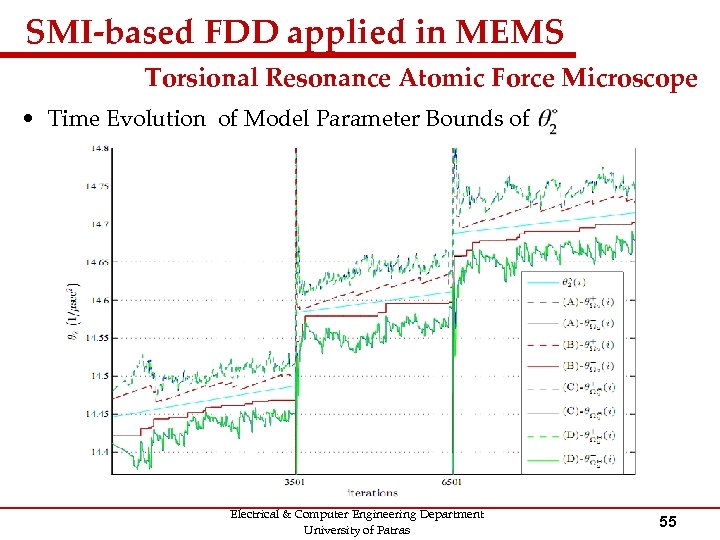
SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • Time Evolution of Model Parameter Bounds of Electrical & Computer Engineering Department University of Patras 55
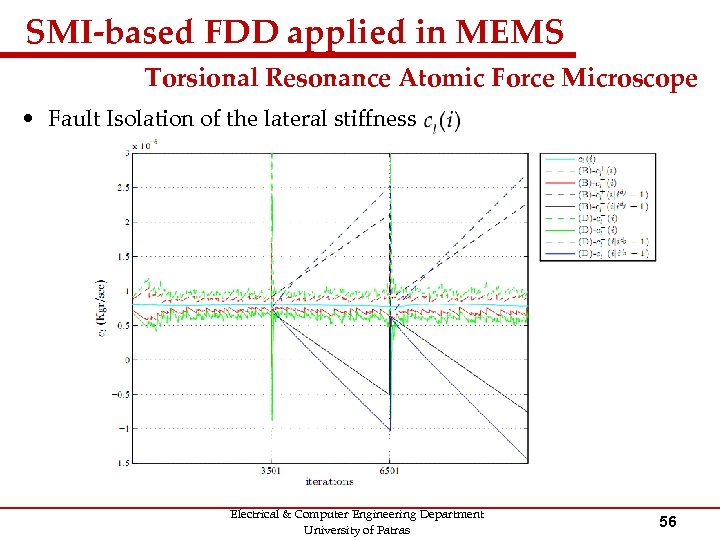
SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • Fault Isolation of the lateral stiffness Electrical & Computer Engineering Department University of Patras 56
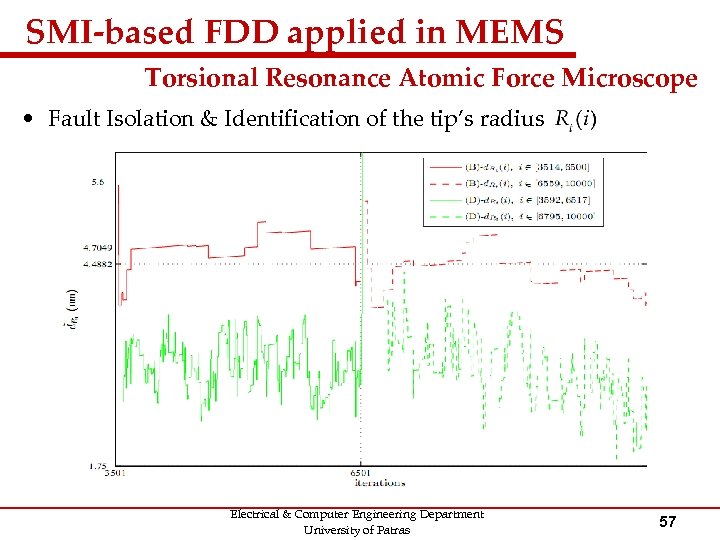
SMI-based FDD applied in MEMS Torsional Resonance Atomic Force Microscope • Fault Isolation & Identification of the tip’s radius Electrical & Computer Engineering Department University of Patras 57

Concluding Remarks • Design of methods for detecting and diagnosing multiple abrupt parametric faults • Fault Detection and Diagnosis methods relying on Set Membership Identification – Development of an Orthotopic SMI algorithm handling both data-hyperstrips and data-hypersectors – Utilization of an ellipsoid based SMI algorithm (OVE) handling data-hyperstrips and modification of the OVE for handling data-hypersectors • Fault Detection based on a) the intersection of the outer bounding parametric sets and the data-hyperspace, b) the intersection of support orthotopes of ellipsoids • Resetting procedure based on set theoretic operations Electrical & Computer Engineering Department University of Patras 58

Concluding Remarks • Generation of fault isolation and identification criteria based on set projections • Development of a backward-in-time procedure for a more accurate specification of the time of fault occurrence • the application of the proposed FDD methods for capturing multiple abrupt failure modes appeared in a parallel-plate electrostatic microactuator, • the lumped parameter modelling of a torsional-resonant Atomic Force Microscope for the application of the FDD methods so as to capture abrupt fractures of the tip's radius. Electrical & Computer Engineering Department University of Patras 59

Future Work • Design of Fault Detection and Diagnosis method – aiming at the detection and diagnosis of both additive and multiplicative faults, – using a linearly parametrizable model with – implementing a SMI algorithm using the intersection of datahypersectors and data-hyperstrips or executing in parallel the algorithms with data-hypersectors and data-hyperstrips • Investigation of the detectability of the faults via the FDD methods – using a range of input stimuli, noise bounds, parameter perturbation bounds e. t. c, – applied in closed-loop systems • Experimental verification of the efficiency of the proposed FDD methods applied in a real MEMS application Electrical & Computer Engineering Department University of Patras 60
![Dissertation Publications Journal Publications [J. 1] V. Reppa and A. Tzes, Fault Detection and Dissertation Publications Journal Publications [J. 1] V. Reppa and A. Tzes, Fault Detection and](https://present5.com/presentation/de2dfc6e158c1ade7b847a2fea1f51a6/image-61.jpg)
Dissertation Publications Journal Publications [J. 1] V. Reppa and A. Tzes, Fault Detection and Diagnosis based on Parameter Set estimation, to appear in IET Journal of Control Theory and Applications Conference Publications [C. 1] V. Reppa and A. Tzes, Fault Detection and Diagnosis relying on Set Membership Identification for Time Varying Systems, submitted in Conference on Control and Fault -Tolerant Systems, Nice, France, 2010 [C. 2] V. Reppa, M. Vagia and A. Tzes, Fault Detection and Diagnosis enhanced by a Reconfiguration Control Scheme for a Micro-Electrostatic Actuator, in Proceedings of the 18 th Mediterranean Conference on Control and Applications, Marrakech, Morocco, 2010, pp. 477 -482. [C. 3] V. Reppa and A. Tzes, Fault Detection and Diagnosis based on Parameter Set Estimation for Measurements corrupted by Bounded Noise, in Proceedings of the 18 th Mediterranean Conference on Control and Applications, Marrakech, Morocco, 2010, pp. 460 -465. [C. 4] V. Reppa and A. Tzes, Fault Detection relying on Set Membership Techniques for an Atomic Force Microscope, in Proceedings of the 7 th IFAC Symposium on Fault Detection, Supervision and Safety on Technical Processes (SAFEPROCESS), Barcelona, Spain, 2009, pp. 1186 -1191 Electrical & Computer Engineering Department University of Patras 61
![Dissertation Publications • Conference Publications [C. 5] V. Reppa and A. Tzes, Fault Detection Dissertation Publications • Conference Publications [C. 5] V. Reppa and A. Tzes, Fault Detection](https://present5.com/presentation/de2dfc6e158c1ade7b847a2fea1f51a6/image-62.jpg)
Dissertation Publications • Conference Publications [C. 5] V. Reppa and A. Tzes, Fault Detection based on Orthotopic Set Membership Identification for Robot Manipulators, in Proceedings of the 17 th IFAC World Congress, Seoul, Korea, 2008, pp. 7344 -7349 [C. 6] V. Reppa, M. Vagia and A. Tzes, Fault Detection using Set Membership Identification for Micro-Electrostatic Actuators, in Proceedings of IEEE International Conference on Control Applications, Singapore, 2007, pp. 789 -794 [C. 7] V. Reppa and A. Tzes, Synergy between control and electronic simulation models in performance system enhancement, in Proceedings of IEEE International Conference on Control Applications, Singapore, 2007, pp. 1138 -1143 [C. 8] V. Reppa and A. Tzes , Application of Set Membership Identification for Fault Detection of MEMS in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 06), Orlando, Florida, 2006, pp. 643 -648 Electrical & Computer Engineering Department University of Patras 62
de2dfc6e158c1ade7b847a2fea1f51a6.ppt