79f44e24ffc3a551cb8c16e991dada59.ppt
- Количество слайдов: 58

Object-Oriented Programming -- Using C++ Andres, Wen-Yuan Liao Department of Computer Science and Engineering De Lin Institute of Technology andres@dlit. edu. tw http: //cse. dlit. edu. tw/~andres 1

Chapter 17 - Data Structures Outline 17. 1 Introduction 17. 2 Self-Referential Classes 17. 3 Dynamic Memory Allocation and Data Structures 17. 4 Linked Lists 17. 5 Stacks 17. 6 Queues 17. 7 Trees 2

17. 1 Introduction • Fixed-size data structures – Arrays, structs • Dynamic data structures – Grow and shrink as program runs – Linked lists • Insert/remove items anywhere – Stacks • Insert/remove from top of stack – Queues • Like a line, insert at back, remove from front – Binary trees • High-speed searching/sorting of data 3
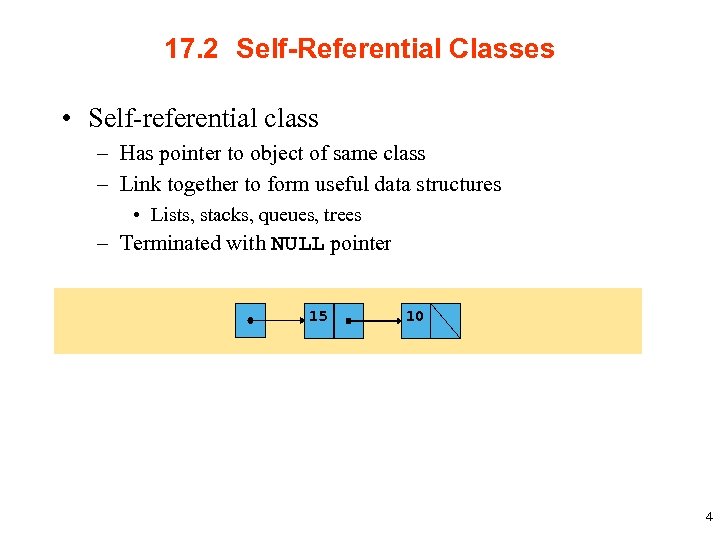
17. 2 Self-Referential Classes • Self-referential class – Has pointer to object of same class – Link together to form useful data structures • Lists, stacks, queues, trees – Terminated with NULL pointer 15 10 4

17. 2 Self-Referential Classes • Sample code Class Node - int data; class Node { -NODE *next. Ptr; public: Node( int ); void set. Data( int ); int get. Data() const; void set. Next. Ptr( Node * ); Node const Node *get. Next. Ptr() const; private: int data; Node *next. Ptr; }; • Pointer to object called a link – next. Ptr points to a Node 5

17. 3 Dynamic Memory Allocation and Data Structures • Dynamic memory allocation – Obtain and release memory during program execution – Create and remove nodes • Operator new – Takes type of object to create – Returns pointer to newly created object • Node *new. Ptr = new Node( 10 ); • Returns bad_alloc if not enough memory • 10 is the node's object data 6

17. 3 Dynamic Memory Allocation and Data Structures • Operator delete – delete new. Ptr; – Deallocates memory allocated by new, calls destructor – Memory returned to system, can be used in future • new. Ptr not deleted, only the space it points to 7

17. 4 Linked Lists • Linked list – Collection of self-referential class objects (nodes) connected by pointers (links) – Accessed using pointer to first node of list • Subsequent nodes accessed using the links in each node – Link in last node is null (zero) • Indicates end of list – Data stored dynamically • Nodes created as necessary • Node can have data of any type 8
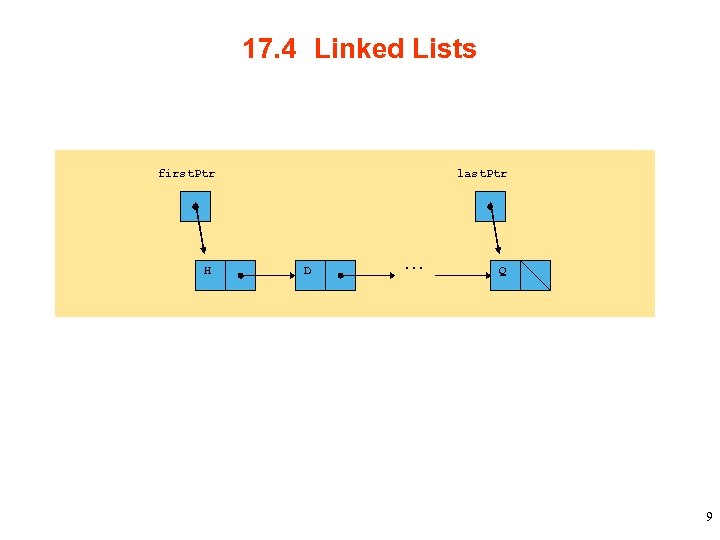
17. 4 Linked Lists first. Ptr H last. Ptr D . . . Q 9

17. 4 Linked Lists • Linked lists vs. arrays – Arrays can become full • Allocating "extra" space in array wasteful, may never be used • Linked lists can grow/shrink as needed • Linked lists only become full when system runs out of memory – Linked lists can be maintained in sorted order • Insert element at proper position • Existing elements do not need to be moved 10

17. 4 Linked Lists • Selected linked list operations – – Insert node at front Insert node at back Remove node from front Remove node from back • In following illustrations – List has first. Ptr and last. Ptr – (a) is before, (b) is after 11
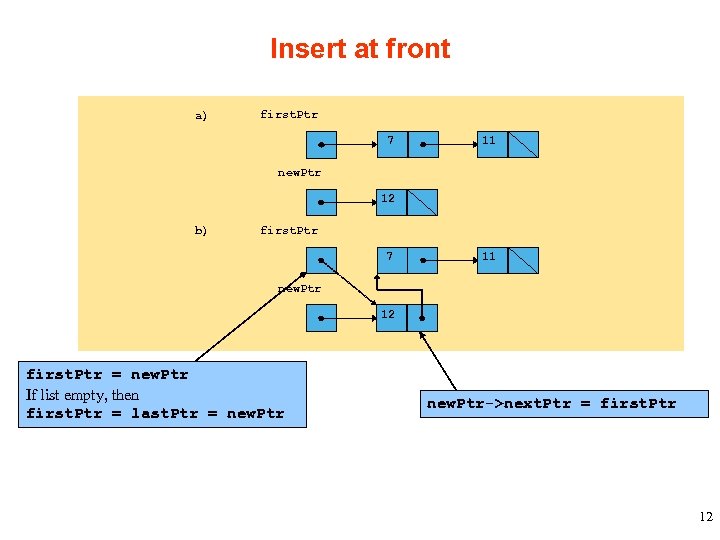
Insert at front a) first. Ptr 7 11 new. Ptr 12 b) first. Ptr 7 11 new. Ptr 12 first. Ptr = new. Ptr If list empty, then first. Ptr = last. Ptr = new. Ptr->next. Ptr = first. Ptr 12
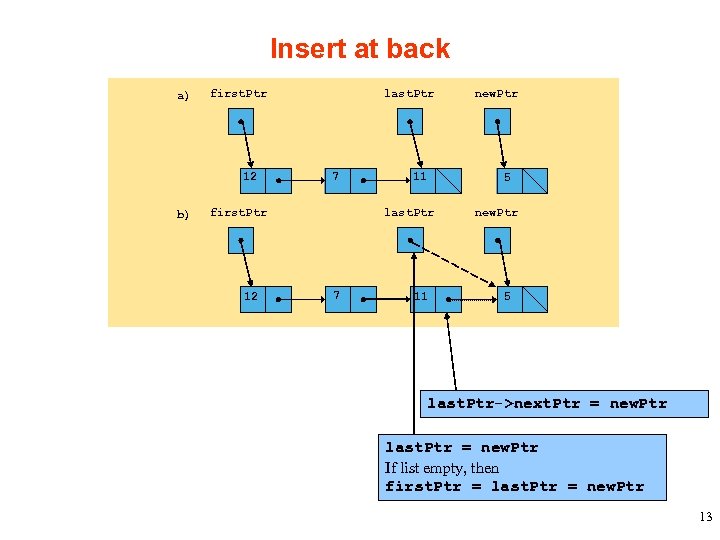
Insert at back a) first. Ptr 12 b) last. Ptr 7 first. Ptr 12 11 last. Ptr 7 11 new. Ptr 5 last. Ptr->next. Ptr = new. Ptr last. Ptr = new. Ptr If list empty, then first. Ptr = last. Ptr = new. Ptr 13
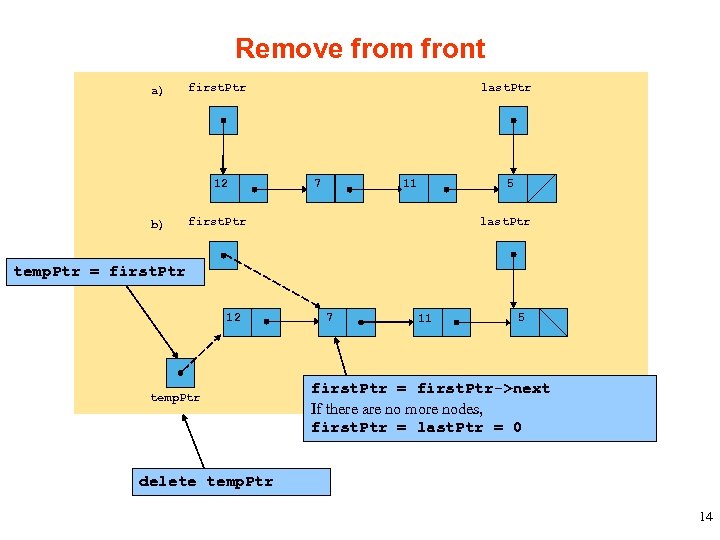
Remove from front a) first. Ptr 12 b) last. Ptr 7 11 5 first. Ptr last. Ptr temp. Ptr = first. Ptr 12 temp. Ptr 7 11 5 first. Ptr = first. Ptr->next If there are no more nodes, first. Ptr = last. Ptr = 0 delete temp. Ptr 14
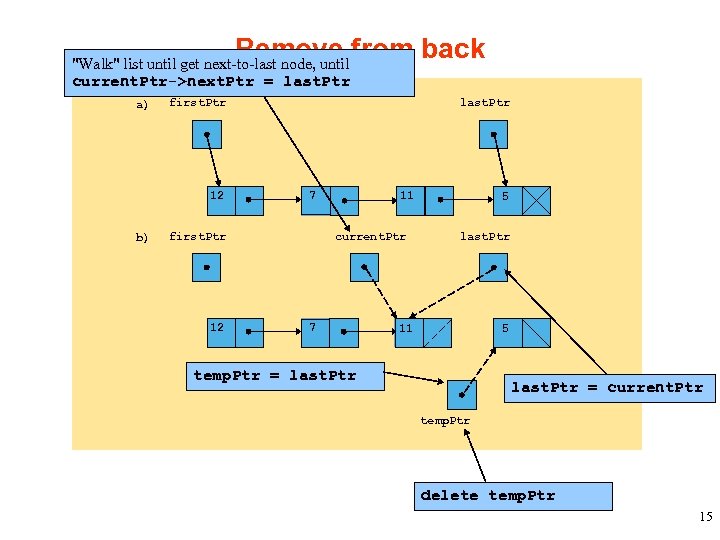
Remove from back "Walk" list until get next-to-last node, until current. Ptr->next. Ptr = last. Ptr a) first. Ptr 12 b) last. Ptr current. Ptr first. Ptr 12 11 7 7 5 last. Ptr 11 5 temp. Ptr = last. Ptr = current. Ptr temp. Ptr delete temp. Ptr 15

17. 4 Linked Lists • Upcoming program has two class templates – Create two class templates – List. Node data next. Prt • data (type depends on class template) • next. Ptr – List • Linked list of List. Node objects • List manipulation functions – insert. At. Front List. Node 12 – insert. At. Back – remove. From. Front – remove. From. Back List. Node 7 List. Node 11 List. Node 5 16
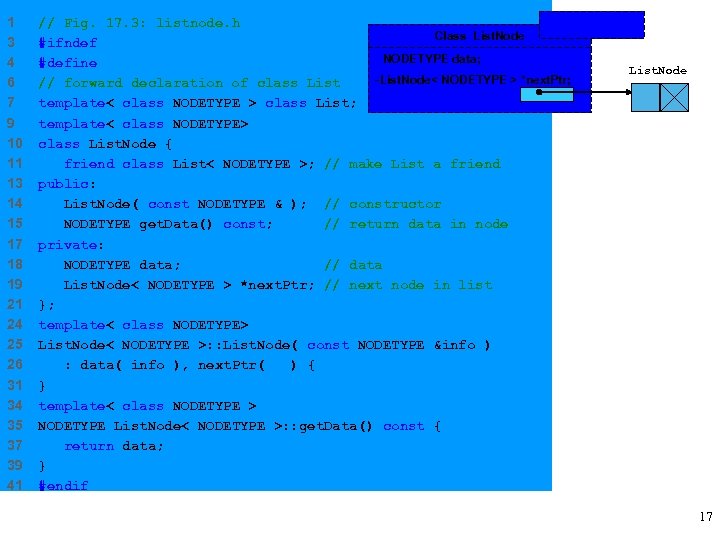
1 3 4 6 7 9 10 11 13 14 15 17 18 19 21 24 25 26 31 34 35 37 39 41 // Fig. 17. 3: listnode. h NODETYPE Class List. Node #ifndef LISTNODE_H - NODETYPE data; #define LISTNODE_H List. Node -List. Node< NODETYPE > *next. Ptr; // forward declaration of class List template< class NODETYPE > class List; template< class NODETYPE> class List. Node { friend class List< NODETYPE >; // make List a friend public: List. Node( const NODETYPE & ); // constructor NODETYPE get. Data() const; // return data in node private: NODETYPE data; // data List. Node< NODETYPE > *next. Ptr; // next node in list }; template< class NODETYPE> List. Node< NODETYPE >: : List. Node( const NODETYPE &info ) : data( info ), next. Ptr( 0 ) { } template< class NODETYPE > NODETYPE List. Node< NODETYPE >: : get. Data() const { return data; } #endif 17
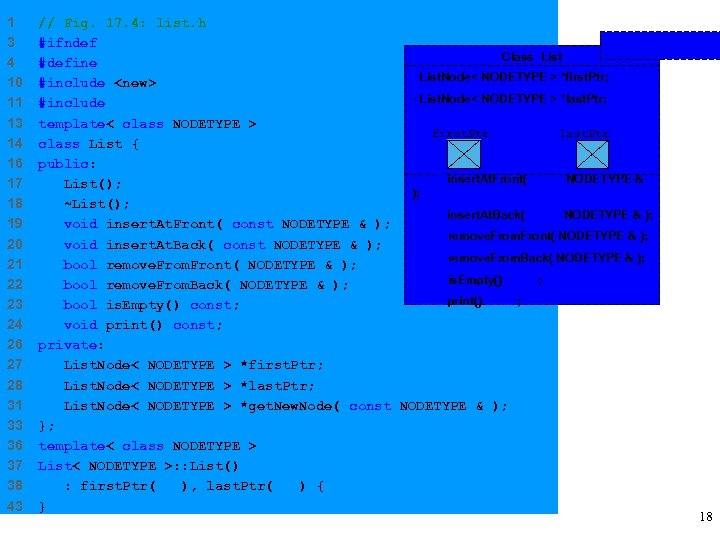
1 3 4 10 11 13 14 16 17 18 19 20 21 22 23 24 26 27 28 31 33 36 37 38 43 // Fig. 17. 4: list. h #ifndef LIST_H NODETYPE Class List #define LIST_H - List. Node< NODETYPE > *first. Ptr; #include <new> - List. Node< NODETYPE > *last. Ptr; #include "listnode. h" template< class NODETYPE > first. Ptr last. Ptr class List { public: +void insert. At. Front( const NODETYPE & List(); ); ~List(); +void insert. At. Back( const NODETYPE & ); void insert. At. Front( const NODETYPE & ); +bool remove. From. Front( NODETYPE & ); void insert. At. Back( const NODETYPE & ); +bool remove. From. Back( NODETYPE & ); bool remove. From. Front( NODETYPE & ); +bool is. Empty() const; bool remove. From. Back( NODETYPE & ); +void print() const; bool is. Empty() const; void print() const; private: List. Node< NODETYPE > *first. Ptr; List. Node< NODETYPE > *last. Ptr; List. Node< NODETYPE > *get. New. Node( const NODETYPE & ); }; template< class NODETYPE > List< NODETYPE >: : List() : first. Ptr( 0 ), last. Ptr( 0 ) { } 18
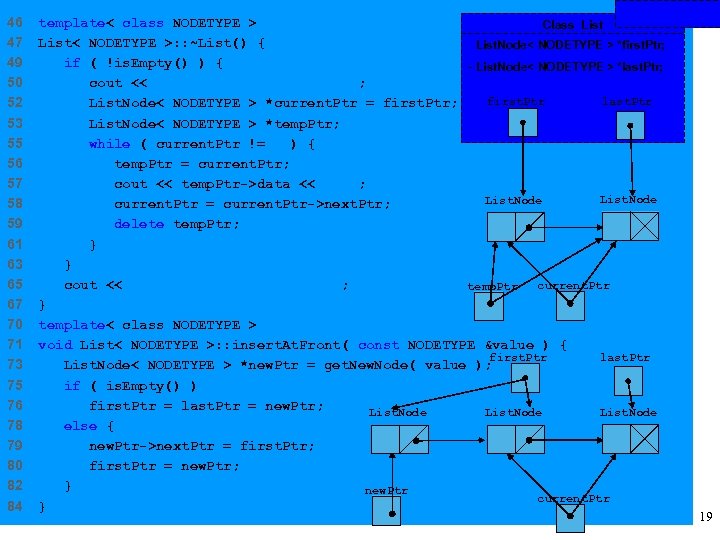
46 47 49 50 52 53 55 56 57 58 59 61 63 65 67 70 71 73 75 76 78 79 80 82 84 NODETYPE template< class NODETYPE > Class List< NODETYPE >: : ~List() { - List. Node< NODETYPE > *first. Ptr; if ( !is. Empty() ) { - List. Node< NODETYPE > *last. Ptr; cout << "Destroying nodes. . . n"; first. Ptr last. Ptr List. Node< NODETYPE > *current. Ptr = first. Ptr; List. Node< NODETYPE > *temp. Ptr; while ( current. Ptr != 0 ) { temp. Ptr = current. Ptr; cout << temp. Ptr->data << 'n'; List. Node current. Ptr = current. Ptr->next. Ptr; delete temp. Ptr; } } cout << "All nodes destroyednn"; current. Ptr temp. Ptr } template< class NODETYPE > void List< NODETYPE >: : insert. At. Front( const NODETYPE &value ) { first. Ptr last. Ptr List. Node< NODETYPE > *new. Ptr = get. New. Node( value ); if ( is. Empty() ) first. Ptr = last. Ptr = new. Ptr; List. Node else { new. Ptr->next. Ptr = first. Ptr; first. Ptr = new. Ptr; } new. Ptr current. Ptr } 19
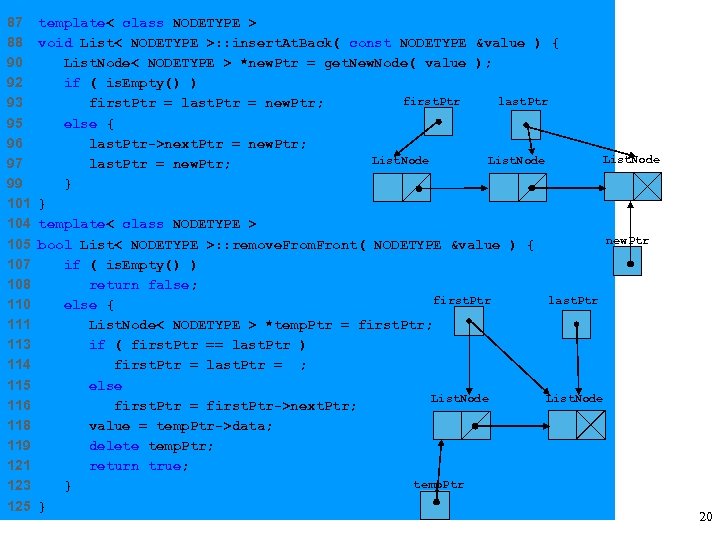
87 88 90 92 93 95 96 97 99 101 104 105 107 108 110 111 113 114 115 116 118 119 121 123 125 template< class NODETYPE > void List< NODETYPE >: : insert. At. Back( const NODETYPE &value ) { List. Node< NODETYPE > *new. Ptr = get. New. Node( value ); if ( is. Empty() ) first. Ptr last. Ptr first. Ptr = last. Ptr = new. Ptr; else { last. Ptr->next. Ptr = new. Ptr; List. Node last. Ptr = new. Ptr; } } template< class NODETYPE > new. Ptr bool List< NODETYPE >: : remove. From. Front( NODETYPE &value ) { if ( is. Empty() ) return false; first. Ptr last. Ptr else { List. Node< NODETYPE > *temp. Ptr = first. Ptr; if ( first. Ptr == last. Ptr ) first. Ptr = last. Ptr = 0; else List. Node first. Ptr = first. Ptr->next. Ptr; value = temp. Ptr->data; delete temp. Ptr; return true; temp. Ptr } } 20
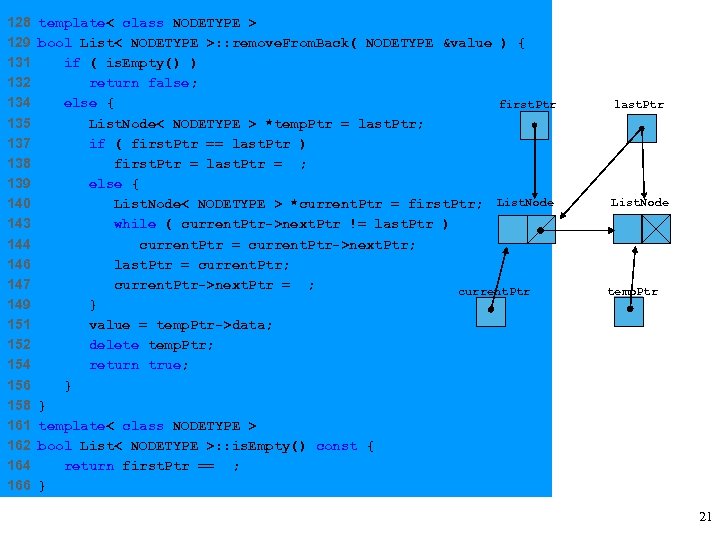
128 129 131 132 134 135 137 138 139 140 143 144 146 147 149 151 152 154 156 158 161 162 164 166 template< class NODETYPE > bool List< NODETYPE >: : remove. From. Back( NODETYPE &value ) { if ( is. Empty() ) return false; else { first. Ptr List. Node< NODETYPE > *temp. Ptr = last. Ptr; if ( first. Ptr == last. Ptr ) first. Ptr = last. Ptr = 0; else { List. Node< NODETYPE > *current. Ptr = first. Ptr; List. Node while ( current. Ptr->next. Ptr != last. Ptr ) current. Ptr = current. Ptr->next. Ptr; last. Ptr = current. Ptr; current. Ptr->next. Ptr = 0; current. Ptr } value = temp. Ptr->data; delete temp. Ptr; return true; } } template< class NODETYPE > bool List< NODETYPE >: : is. Empty() const { return first. Ptr == 0; } last. Ptr List. Node temp. Ptr 21

169 170 171 173 175 178 179 181 182 183 185 187 189 191 192 193 195 197 199 201 template< class NODETYPE > List. Node< NODETYPE > *List< NODETYPE >: : get. New. Node( const NODETYPE &value ) { return new List. Node< NODETYPE >( value ); } template< class NODETYPE > void List< NODETYPE >: : print() const{ if ( is. Empty() ) { cout << "The list is emptynn"; return; } List. Node< NODETYPE > *current. Ptr = first. Ptr; cout << "The list is: "; while ( current. Ptr != 0 ) { cout << current. Ptr->data << ' '; current. Ptr = current. Ptr->next. Ptr; } cout << "nn"; } #endif 22
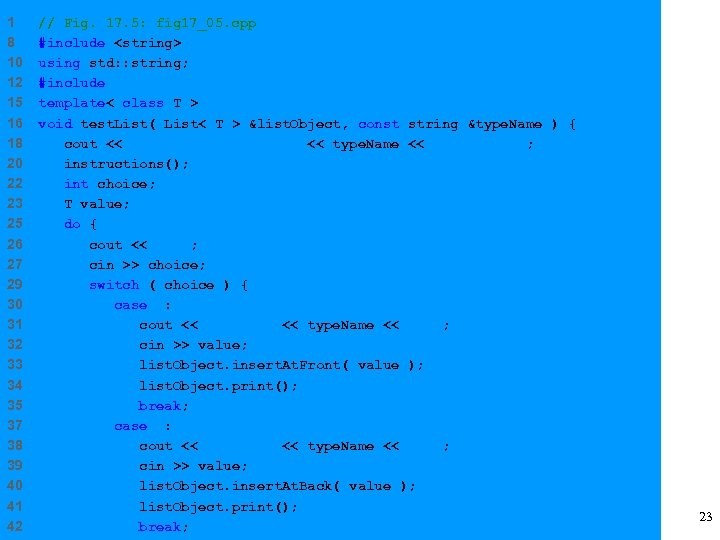
1 8 10 12 15 16 18 20 22 23 25 26 27 29 30 31 32 33 34 35 37 38 39 40 41 42 // Fig. 17. 5: fig 17_05. cpp #include <string> using std: : string; #include "list. h" template< class T > void test. List( List< T > &list. Object, const string &type. Name ) { cout << "Testing a List of " << type. Name << " valuesn"; instructions(); int choice; T value; do { cout << "? "; cin >> choice; switch ( choice ) { case 1: cout << "Enter " << type. Name << ": "; cin >> value; list. Object. insert. At. Front( value ); list. Object. print(); break; case 2: cout << "Enter " << type. Name << ": "; cin >> value; list. Object. insert. At. Back( value ); list. Object. print(); break; 23

44 45 46 48 49 51 52 53 55 56 60 62 64 67 69 70 71 72 73 74 76 78 81 82 85 86 case 3: if ( list. Object. remove. From. Front( value ) ) cout << value << " removed from listn"; list. Object. print(); break; case 4: if ( list. Object. remove. From. Back( value ) ) cout << value << " removed from listn"; list. Object. print(); break; } } while ( choice != 5 ); cout << "End list testnn"; } void instructions() { cout << "Enter one of the following: n" << " 1 to insert at beginning of listn" << " 2 to insert at end of listn" << " 3 to delete from beginning of listn" << " 4 to delete from end of listn" << " 5 to end list processingn"; } int main() { List< int > integer. List; test. List( integer. List, "integer" ); List< double > double. List; test. List( double. List, "double" ); } 24

Testing a List of integer values Enter one of the following: 1 to insert at beginning of list 2 to insert at end of list 3 to delete from beginning of list 4 to delete from end of list 5 to end list processing ? 1 Enter integer: 1 The list is: 1 ? 1 Enter integer: 2 The list is: 2 1 ? 2 Enter integer: 3 The list is: 2 1 3 ? 2 Enter integer: 4 The list is: 2 1 3 4 25

? 3 2 removed from list The list is: 1 3 4 ? 3 1 removed from list The list is: 3 4 ? 4 4 removed from list The list is: 3 ? 4 3 removed from list The list is empty ? 5 End list test 26

Testing a List of double values Enter one of the following: 1 to insert at beginning of list 2 to insert at end of list 3 to delete from beginning of list 4 to delete from end of list 5 to end list processing ? 1 Enter double: 1. 1 The list is: 1. 1 ? 1 Enter double: 2. 2 The list is: 2. 2 1. 1 ? 2 Enter double: 3. 3 The list is: 2. 2 1. 1 3. 3 ? 2 Enter double: 4. 4 The list is: 2. 2 1. 1 3. 3 4. 4 ? 3 2. 2 removed from list The list is: 1. 1 3. 3 4. 4 27

? 3 1. 1 removed from list The list is: 3. 3 4. 4 ? 4 4. 4 removed from list The list is: 3. 3 ? 4 3. 3 removed from list The list is empty ? 5 End list test All nodes destroyed 28

17. 4 Linked Lists • Types of linked lists – Singly linked list (used in example) • Pointer to first node • Travel in one direction (null-terminated) – Circular, singly-linked • As above, but last node points to first – Doubly-linked list • Each node has a forward and backwards pointer • Travel forward or backward • Last node null-terminated – Circular, double-linked • As above, but first and last node joined 29

17. 5 Stacks • Stack – Nodes can be added/removed from top • Constrained version of linked list • Like a stack of plates – Last-in, first-out (LIFO) data structure – Bottom of stack has null link • Stack operations – Push: add node to top – Pop: remove node from top • Stores value in reference variable 30

17. 5 Stacks • Stack applications – Function calls: know how to return to caller • Return address pushed on stack • Most recent function call on top • If function A calls B which calls C: – Used to store automatic variables • Popped of stack when no longer needed – Used by compilers • Example in the exercises in book 31

17. 5 Stacks • Upcoming program – Create stack from list • insert. At. Front, remove. From. Front – Software reusability • Inheritance – Stack inherits from List • Composition – Stack contains a private List object – Performs operations on that object – Makes stack implementation simple 32
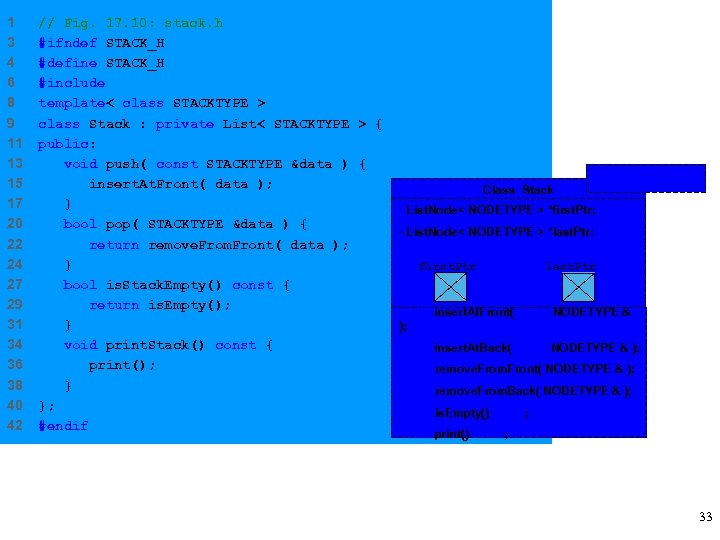
1 3 4 6 8 9 11 13 15 17 20 22 24 27 29 31 34 36 38 40 42 // Fig. 17. 10: stack. h #ifndef STACK_H #define STACK_H #include "list. h" template< class STACKTYPE > class Stack : private List< STACKTYPE > { public: void push( const STACKTYPE &data ) { insert. At. Front( data ); } bool pop( STACKTYPE &data ) { return remove. From. Front( data ); } bool is. Stack. Empty() const { return is. Empty(); } void print. Stack() const { print(); } }; #endif Class Stack STACKTYPE - List. Node< NODETYPE > *first. Ptr; - List. Node< NODETYPE > *last. Ptr; first. Ptr last. Ptr +void insert. At. Front( const NODETYPE & ); +void insert. At. Back( const NODETYPE & ); +bool remove. From. Front( NODETYPE & ); +bool remove. From. Back( NODETYPE & ); +bool is. Empty() const; +void print() const; 33
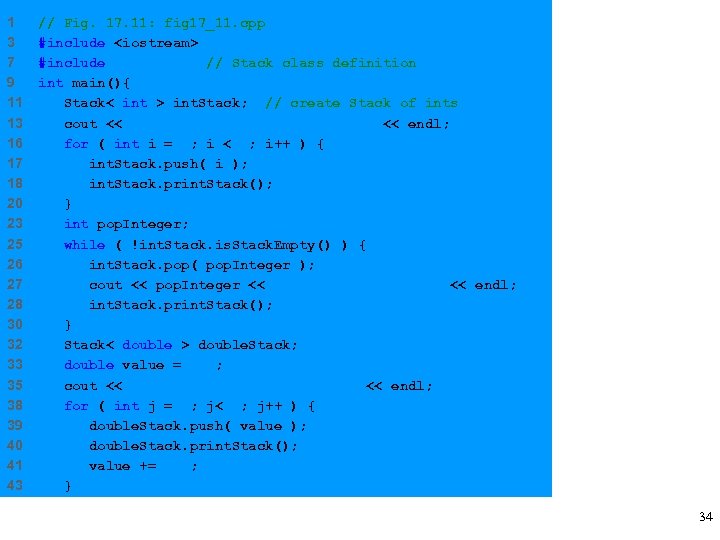
1 3 7 9 11 13 16 17 18 20 23 25 26 27 28 30 32 33 35 38 39 40 41 43 // Fig. 17. 11: fig 17_11. cpp #include <iostream> #include "stack. h" // Stack class definition int main(){ Stack< int > int. Stack; // create Stack of ints cout << "processing an integer Stack" << endl; for ( int i = 0; i < 4; i++ ) { int. Stack. push( i ); int. Stack. print. Stack(); } int pop. Integer; while ( !int. Stack. is. Stack. Empty() ) { int. Stack. pop( pop. Integer ); cout << pop. Integer << " popped from stack" << endl; int. Stack. print. Stack(); } Stack< double > double. Stack; double value = 1. 1; cout << "processing a double Stack" << endl; for ( int j = 0; j< 4; j++ ) { double. Stack. push( value ); double. Stack. print. Stack(); value += 1. 1; } 34

46 48 49 50 51 53 55 57 double pop. Double; while ( !double. Stack. is. Stack. Empty() ) { double. Stack. pop( pop. Double ); cout << pop. Double << " popped from stack" << endl; double. Stack. print. Stack(); } return 0; } 35

processing an integer Stack The list is: 0 The list is: 1 0 The list is: 2 1 0 The list is: 3 2 1 0 3 popped from stack The list is: 2 1 0 2 popped from stack The list is: 1 0 1 popped from stack The list is: 0 0 popped from stack The list is empty processing a double Stack The list is: 1. 1 The list is: 2. 2 1. 1 The list is: 3. 3 2. 2 1. 1 36

The list is: 4. 4 3. 3 2. 2 1. 1 4. 4 popped from stack The list is: 3. 3 2. 2 1. 1 3. 3 popped from stack The list is: 2. 2 1. 1 2. 2 popped from stack The list is: 1. 1 popped from stack The list is empty All nodes destroyed 37
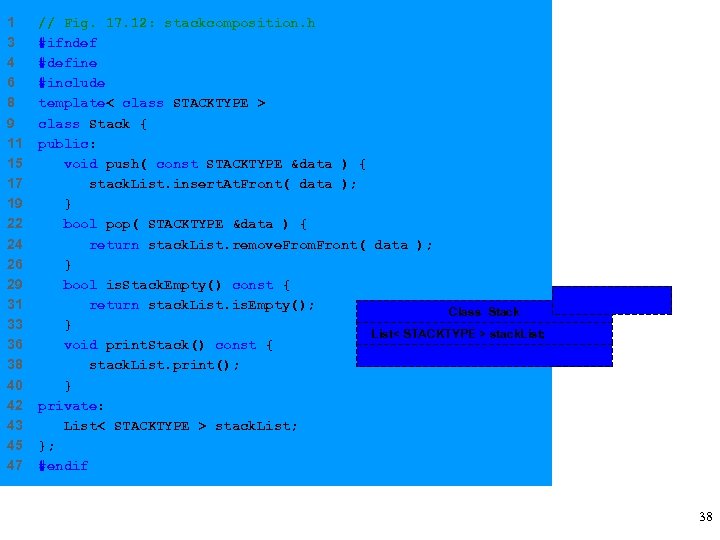
1 3 4 6 8 9 11 15 17 19 22 24 26 29 31 33 36 38 40 42 43 45 47 // Fig. 17. 12: stackcomposition. h #ifndef STACKCOMPOSITION #define STACKCOMPOSITION #include "list. h" template< class STACKTYPE > class Stack { public: void push( const STACKTYPE &data ) { stack. List. insert. At. Front( data ); } bool pop( STACKTYPE &data ) { return stack. List. remove. From. Front( data ); } bool is. Stack. Empty() const { return stack. List. is. Empty(); Class Stack } - List< STACKTYPE > stack. List; void print. Stack() const { stack. List. print(); } private: List< STACKTYPE > stack. List; }; #endif STACKTYPE 38

17. 6 Queues • Queue – – Like waiting in line Nodes added to back (tail), removed from front (head) First-in, first-out (FIFO) data structure Insert/remove called enqueue/dequeue • Applications – Print spooling • Documents wait in queue until printer available – Packets on network – File requests from server 39

17. 6 Queues • Upcoming program – Queue implementation – Reuse List as before • insert. At. Back (enqueue) • remove. From. Front (dequeue) 40

1 3 4 6 8 9 11 13 15 17 20 22 24 27 29 31 34 36 38 40 42 // Fig. 17. 13: queue. h #ifndef QUEUE_H #define QUEUE_H #include "list. h" template< class QUEUETYPE > class Queue : private List< QUEUETYPE > { public: void enqueue( const QUEUETYPE &data ) { insert. At. Back( data ); QUEUETYPE Class Queue } - List. Node< NODETYPE > *first. Ptr; bool dequeue( QUEUETYPE &data ) { - List. Node< NODETYPE > *last. Ptr; return remove. From. Front( data ); } first. Ptr last. Ptr bool is. Queue. Empty() const { return is. Empty(); +void insert. At. Front( const NODETYPE & } ); void print. Queue() const { +void insert. At. Back( const NODETYPE & ); print(); +bool remove. From. Front( NODETYPE & ); } +bool remove. From. Back( NODETYPE & ); }; +bool is. Empty() const; #endif +void print() const; 41

1 9 11 16 17 18 20 23 25 26 27 28 30 32 33 38 39 40 41 46 48 49 50 51 52 57 // Fig. 17. 14: fig 17_14. cpp int main() { Queue< int > int. Queue; for ( int i = 0; i < 4; i++ ) { int. Queue. enqueue( i ); int. Queue. print. Queue(); } int dequeue. Integer; while ( !int. Queue. is. Queue. Empty() ) { int. Queue. dequeue( dequeue. Integer ); cout << dequeue. Integer << " dequeued" << endl; int. Queue. print. Queue(); } Queue< double > double. Queue; double value = 1. 1; for ( int j = 0; j< 4; j++ ) { double. Queue. enqueue( value ); double. Queue. print. Queue(); value += 1. 1; } double dequeue. Double; while ( !double. Queue. is. Queue. Empty() ) { double. Queue. dequeue( dequeue. Double ); cout << dequeue. Double << " dequeued" << endl; double. Queue. print. Queue(); } } 42

processing an integer Queue The list is: 0 1 2 3 0 dequeued The list is: 1 2 3 1 dequeued The list is: 2 3 2 dequeued The list is: 3 3 dequeued The list is empty processing a double Queue The list is: 1. 1 2. 2 43

The list is: 1. 1 2. 2 3. 3 4. 4 1. 1 dequeued The list is: 2. 2 3. 3 4. 4 2. 2 dequeued The list is: 3. 3 4. 4 3. 3 dequeued The list is: 4. 4 dequeued The list is empty All nodes destroyed 44

17. 7 Trees • Linear data structures – Lists, queues, stacks • Trees – Nonlinear, two-dimensional – Tree nodes have 2 or more links – Binary trees have exactly 2 links/node • None, both, or one link can be null 45

17. 7 Trees • Terminology – Root node: first node on tree – Link refers to child of node • Left child is root of left subtree • Right child is root of right subtree – Leaf node: node with no children – Trees drawn from root downwards B A D C 46

17. 7 Trees • Binary search tree – Values in left subtree less than parent node – Values in right subtree greater than parent • Does not allow duplicate values (good way to remove them) – Fast searches, log 2 n comparisons for a balanced tree 47 25 11 7 17 77 43 31 44 65 93 68 47

17. 7 Trees • Inserting nodes – – Use recursive function Begin at root If current node empty, insert new node here (base case) Otherwise, • If value > node, insert into right subtree • If value < node, insert into left subtree • If neither > nor <, must be = – Ignore duplicate 48

17. 7 Trees • Tree traversals – In-order (print tree values from least to greatest) • Traverse left subtree (call function again) • Print node • Traverse right subtree – Preorder • Print node • Traverse left subtree • Traverse right subtree – Postorder • Traverse left subtree • Traverse rigth subtree • Print node 49

17. 7 Trees • Upcoming program – Create 2 template classes – Tree. Node • data • left. Ptr • right. Ptr – Tree • root. Ptr • Functions – Insert. Node – in. Order. Traversal – pre. Order. Traversal – post. Order. Traversal 50
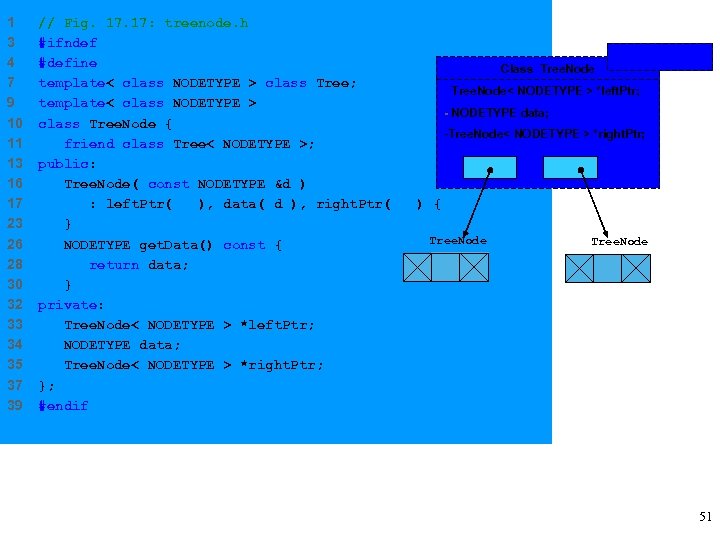
1 3 4 7 9 10 11 13 16 17 23 26 28 30 32 33 34 35 37 39 // Fig. 17: treenode. h #ifndef TREENODE_H NODETYPE #define TREENODE_H Class Tree. Node template< class NODETYPE > class Tree; - Tree. Node< NODETYPE > *left. Ptr; template< class NODETYPE > - NODETYPE data; class Tree. Node { -Tree. Node< NODETYPE > *right. Ptr; friend class Tree< NODETYPE >; public: Tree. Node( const NODETYPE &d ) : left. Ptr( 0 ), data( d ), right. Ptr( 0 ) { } Tree. Node NODETYPE get. Data() const { return data; } private: Tree. Node< NODETYPE > *left. Ptr; NODETYPE data; Tree. Node< NODETYPE > *right. Ptr; }; #endif 51
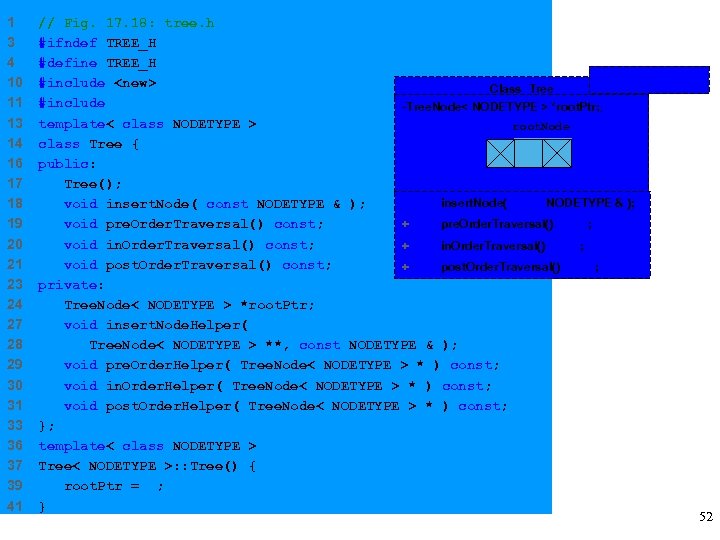
1 3 4 10 11 13 14 16 17 18 19 20 21 23 24 27 28 29 30 31 33 36 37 39 41 // Fig. 17. 18: tree. h #ifndef TREE_H #define TREE_H NODETYPE #include <new> Class Tree #include "treenode. h" -Tree. Node< NODETYPE > *root. Ptr; ; template< class NODETYPE > root. Node class Tree { public: Tree(); + void insert. Node( const NODETYPE & ); + void pre. Order. Traversal() const; void in. Order. Traversal() const; + void in. Order. Traversal() const; void post. Order. Traversal() const; + void post. Order. Traversal() const; private: Tree. Node< NODETYPE > *root. Ptr; void insert. Node. Helper( Tree. Node< NODETYPE > **, const NODETYPE & ); void pre. Order. Helper( Tree. Node< NODETYPE > * ) const; void in. Order. Helper( Tree. Node< NODETYPE > * ) const; void post. Order. Helper( Tree. Node< NODETYPE > * ) const; }; template< class NODETYPE > Tree< NODETYPE >: : Tree() { root. Ptr = 0; } 52
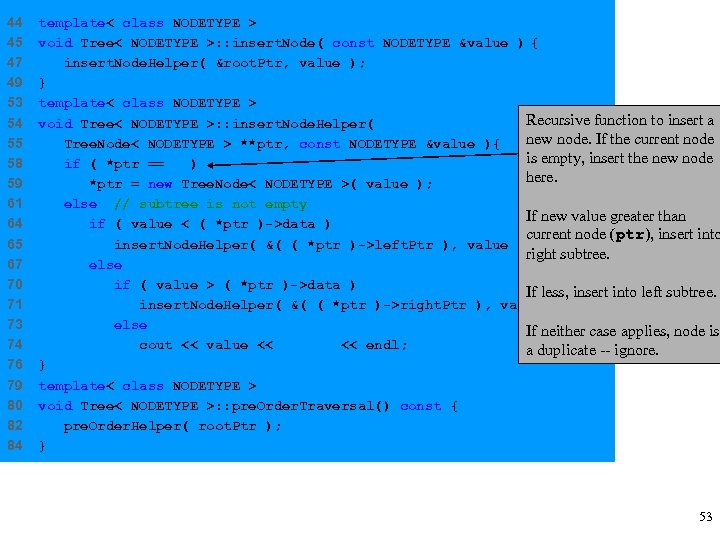
44 45 47 49 53 54 55 58 59 61 64 65 67 70 71 73 74 76 79 80 82 84 template< class NODETYPE > void Tree< NODETYPE >: : insert. Node( const NODETYPE &value ) { insert. Node. Helper( &root. Ptr, value ); } template< class NODETYPE > Recursive function to insert a void Tree< NODETYPE >: : insert. Node. Helper( new node. If the current node Tree. Node< NODETYPE > **ptr, const NODETYPE &value ){ is empty, insert the new node if ( *ptr == 0 ) here. *ptr = new Tree. Node< NODETYPE >( value ); else // subtree is not empty If new value greater than if ( value < ( *ptr )->data ) current node (ptr), insert into insert. Node. Helper( &( ( *ptr )->left. Ptr ), value ); right subtree. else if ( value > ( *ptr )->data ) If less, insert into left subtree. insert. Node. Helper( &( ( *ptr )->right. Ptr ), value ); else If neither case applies, node is cout << value << " dup" << endl; a duplicate -- ignore. } template< class NODETYPE > void Tree< NODETYPE >: : pre. Order. Traversal() const { pre. Order. Helper( root. Ptr ); } 53

87 88 89 91 92 93 94 96 98 101 102 104 106 109 110 111 113 114 115 116 118 120 template< class NODETYPE > void Tree< NODETYPE >: : pre. Order. Helper( Preorder: print, left, right Tree. Node< NODETYPE > *ptr ) const { if ( ptr != 0 ) { cout << ptr->data << ' '; // process node pre. Order. Helper( ptr->left. Ptr ); // go to left subtree pre. Order. Helper( ptr->right. Ptr ); // go to right subtree } } template< class NODETYPE > void Tree< NODETYPE >: : in. Order. Traversal() const { in. Order. Helper( root. Ptr ); } template< class NODETYPE > void Tree< NODETYPE >: : in. Order. Helper( In order: left, print, right Tree. Node< NODETYPE > *ptr ) const { if ( ptr != 0 ) { in. Order. Helper( ptr->left. Ptr ); // go to left subtree cout << ptr->data << ' '; // process node in. Order. Helper( ptr->right. Ptr ); // go to right subtree } } 54
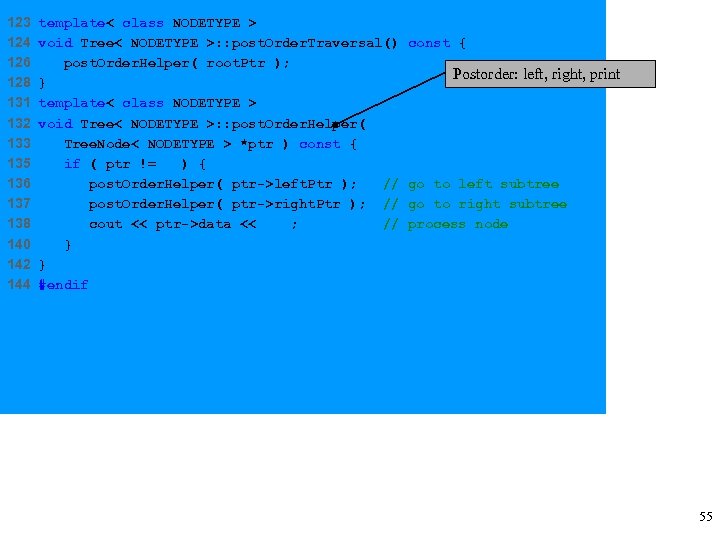
123 124 126 128 131 132 133 135 136 137 138 140 142 144 template< class NODETYPE > void Tree< NODETYPE >: : post. Order. Traversal() post. Order. Helper( root. Ptr ); } template< class NODETYPE > void Tree< NODETYPE >: : post. Order. Helper( Tree. Node< NODETYPE > *ptr ) const { if ( ptr != 0 ) { post. Order. Helper( ptr->left. Ptr ); // post. Order. Helper( ptr->right. Ptr ); // cout << ptr->data << ' '; // } } #endif const { Postorder: left, right, print go to left subtree go to right subtree process node 55
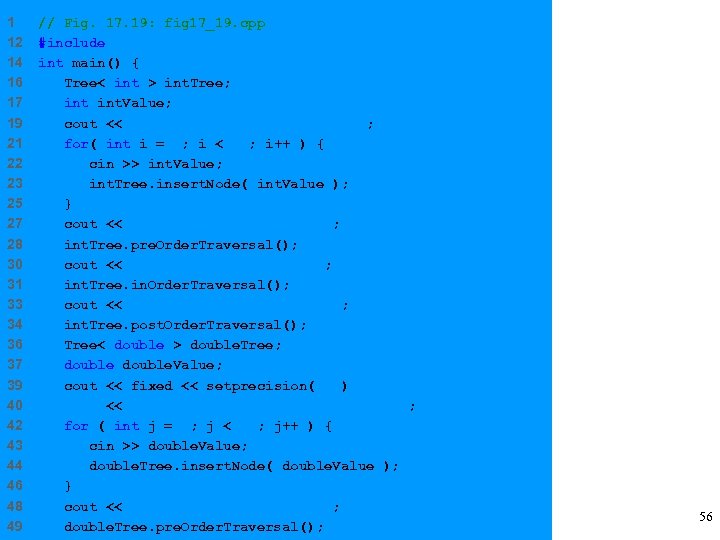
1 12 14 16 17 19 21 22 23 25 27 28 30 31 33 34 36 37 39 40 42 43 44 46 48 49 // Fig. 17. 19: fig 17_19. cpp #include "tree. h" int main() { Tree< int > int. Tree; int. Value; cout << "Enter 10 integer values: n"; for( int i = 0; i < 10; i++ ) { cin >> int. Value; int. Tree. insert. Node( int. Value ); } cout << "n. Preorder traversaln"; int. Tree. pre. Order. Traversal(); cout << "n. Inorder traversaln"; int. Tree. in. Order. Traversal(); cout << "n. Postorder traversaln"; int. Tree. post. Order. Traversal(); Tree< double > double. Tree; double. Value; cout << fixed << setprecision( 1 ) << "nnn. Enter 10 double values: n"; for ( int j = 0; j < 10; j++ ) { cin >> double. Value; double. Tree. insert. Node( double. Value ); } cout << "n. Preorder traversaln"; double. Tree. pre. Order. Traversal(); 56
51 52 54 55 57 59 61 cout << "n. Inorder traversaln"; double. Tree. in. Order. Traversal(); cout << "n. Postorder traversaln"; double. Tree. post. Order. Traversal(); cout << endl; return 0; } Enter 10 integer values: 50 25 75 12 33 67 88 6 13 68 Preorder traversal 50 25 12 6 13 33 75 67 68 88 Inorder traversal 6 12 13 25 33 50 67 68 75 88 Postorder traversal 6 13 12 33 25 68 67 88 75 50 Enter 10 double values: 39. 2 16. 5 82. 7 3. 3 65. 2 90. 8 1. 1 4. 4 89. 5 92. 5 57
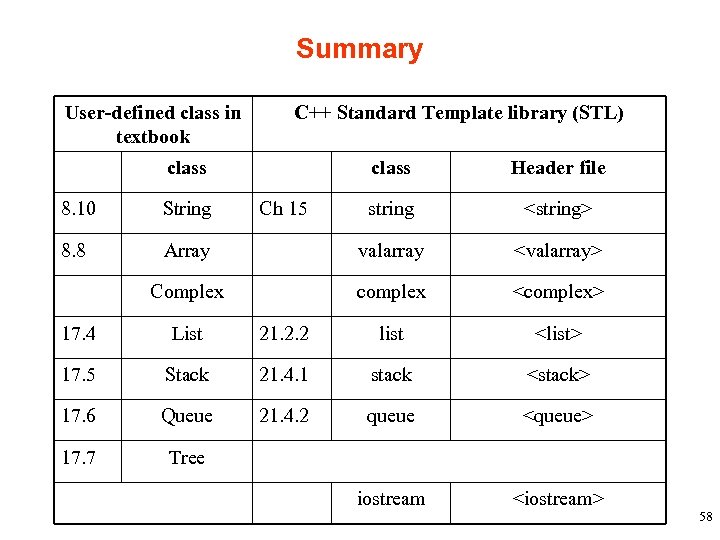
Summary User-defined class in textbook C++ Standard Template library (STL) class Ch 15 Header file string <string> 8. 10 String 8. 8 Array valarray <valarray> Complex complex <complex> 17. 4 List 21. 2. 2 list <list> 17. 5 Stack 21. 4. 1 stack <stack> 17. 6 Queue 21. 4. 2 queue <queue> 17. 7 Tree iostream <iostream> 58
79f44e24ffc3a551cb8c16e991dada59.ppt