Object-oriented Modeling in the Service of Medicine François

Object-oriented Modeling in the Service of Medicine François E. Cellier, ETH Zürich Àngela Nebot, Universitat Politècnica de Catalunya October 25, 2005 ICSC 2005: Beijing Start Presentation

System Complexity and the Understandability of Models • As the systems that are being analyzed by mathematical models have grown in complexity over the years, they have become increasingly difficult to interpret and maintain. • Modelers need to concern themselves with the understandability and maintainability of their models. • Tools need to be developed that support them in this endeavor. October 25, 2005 ICSC 2005: Beijing Start Presentation

Object-oriented Modeling • The object-oriented modeling paradigm enables the modeler to encapsulate knowledge in such a way that snippets of knowledge can be translated to a language familiar to the domain expert. • The complexity of the models is locally contained by encapsulation and hierarchical composition of models. • Models are being made more easily understandable by exploiting the two-dimensional nature of planar graphics. October 25, 2005 ICSC 2005: Beijing Start Presentation

Graphical Modeling • Models of subsystems can be encapsulated as graphical objects, called icons. • The icons can be topologically interconnected to form a two-dimensional network. • Sub-networks of graphical objects can be grouped together to form new objects, for which icons can be designed. In this way, systems can be hierarchically composed from sub-systems forming a tree. • The leaves of the tree must be described by equations. October 25, 2005 ICSC 2005: Beijing Start Presentation

Bond Graph Modeling • Bond graphs are one type of graphical objectoriented models. • They describe the power flow through a physical system. • Since energy and power flow are common to all types of physical systems, bond graphs are domain independent. • The equation-based leaf models of bond graphs can be pre-coded for all domains. October 25, 2005 ICSC 2005: Beijing Start Presentation

The Bond Model • The modeling of physical systems by means of bond graphs operates on a graphical description of energy flows. e f P=e·f e: Effort f: Flow • The energy flows are represented as directed harpoons. The two adjugate variables, which are responsible for the energy flow, are annotated above (intensive: potential variable, “e”) and below (extensive: flow variable, “f”) the harpoon. • The hook of the harpoon always points to the left, and the term “above” refers to the side with the hook. October 25, 2005 ICSC 2005: Beijing Start Presentation

Sources in Bond Graph Representation U 0 va i + U 0 vb Se U 0 i Energy is being Voltage and current added to the system have opposite directions I 0 va I 0 vb Sf u I 0 u October 25, 2005 ICSC 2005: Beijing Start Presentation

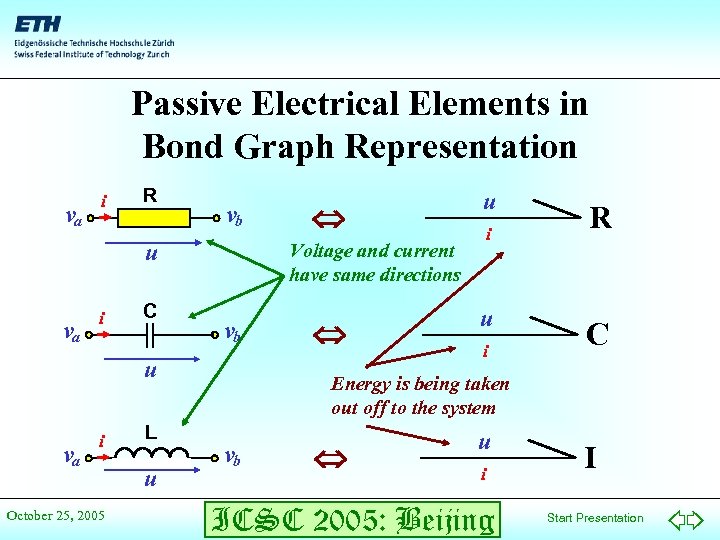
Passive Electrical Elements in Bond Graph Representation va i R vb u va i C va October 25, 2005 L u i Voltage and current have same directions vb u i u u i R C Energy is being taken out off to the system vb u i ICSC 2005: Beijing I Start Presentation

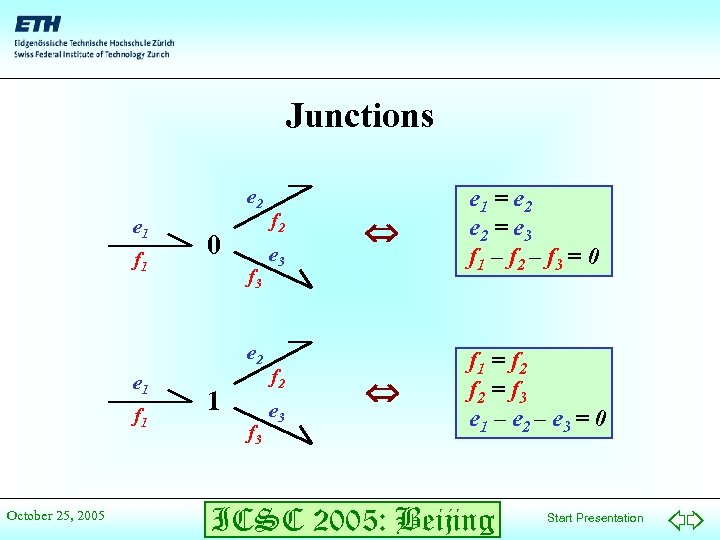
Junctions e 2 e 1 f 1 0 f 3 e 2 e 1 f 1 October 25, 2005 1 f 3 f 2 e 3 e 1 = e 2 = e 3 f 1 – f 2 – f 3 = 0 f 1 = f 2 = f 3 e 1 – e 2 – e 3 = 0 ICSC 2005: Beijing Start Presentation

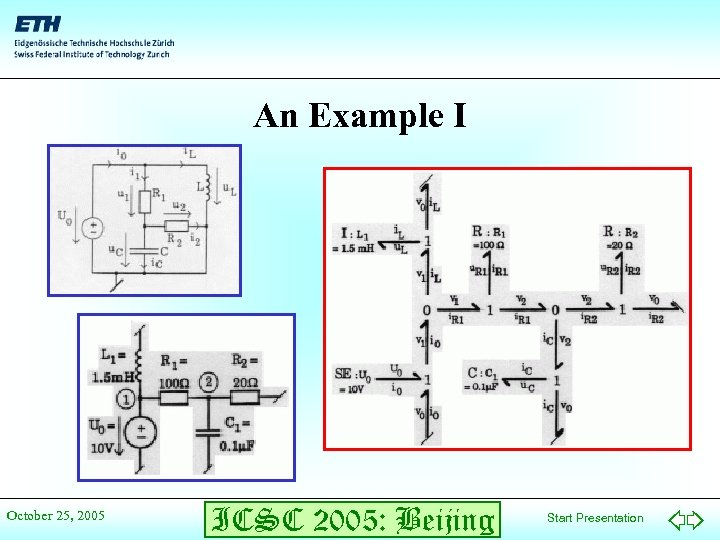
An Example I October 25, 2005 ICSC 2005: Beijing Start Presentation

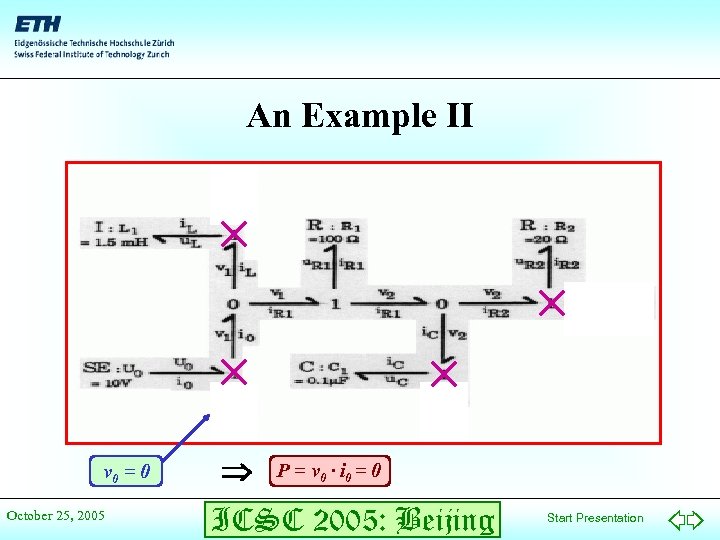
An Example II v 0 = 0 October 25, 2005 P = v 0 · i 0 = 0 ICSC 2005: Beijing Start Presentation

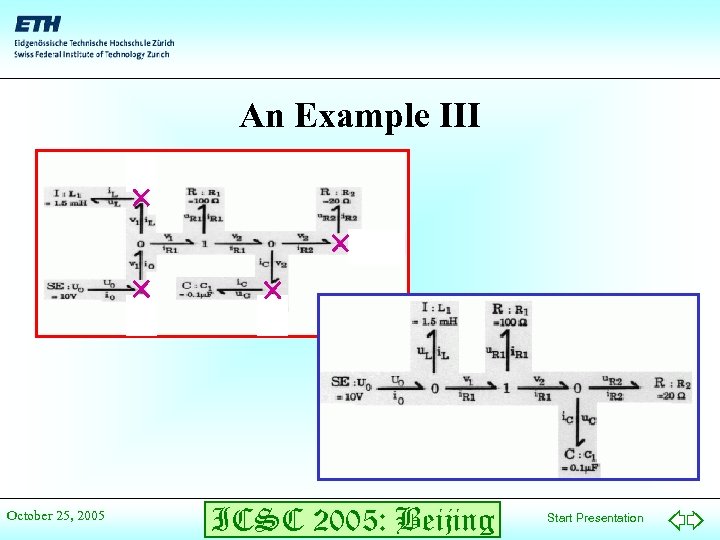
An Example III October 25, 2005 ICSC 2005: Beijing Start Presentation

Causal Bond Graphs • Every bond defines two separate variables, the effort e and the flow f. • Consequently, we need two equations to compute values for these two variables. • It turns out that it is always possible to compute one of the two variables at each side of the bond. • A vertical bar symbolizes the side where the flow is being computed. e f October 25, 2005 ICSC 2005: Beijing Start Presentation

“Causalization” of the Sources The flow has to be computed on the right side. Se U 0 i U 0 = f(t) The source computes the effort. Sf u I 0 = f(t) The source computes the flow. The causality of the sources is fixed. October 25, 2005 ICSC 2005: Beijing Start Presentation

“Causalization” of the Passive Elements u i u R R i u=R·i i=u/R The causality of resistors is free. u i u C I i du/dt = i / C The di/dt = u / I causality of the storage elements is determined by the desire to use integrators instead of differentiators. October 25, 2005 ICSC 2005: Beijing Start Presentation

“Causalization” of the Junctions e 2 e 1 f 1 0 f 3 f 2 e 3 e 2 = e 1 e 3 = e 1 f 1 = f 2 + f 3 Junctions of type 0 have only one flow equation, and therefore, they must have exactly one causality bar. e 2 f 2 = f 1 f 2 e 1 f 3 = f 1 1 e 3 f 1 e 1 = e 2+ e 3 f 3 Junctions of type 1 have only one effort equation, and therefore, they must have exactly (n-1) causality bars. October 25, 2005 ICSC 2005: Beijing Start Presentation

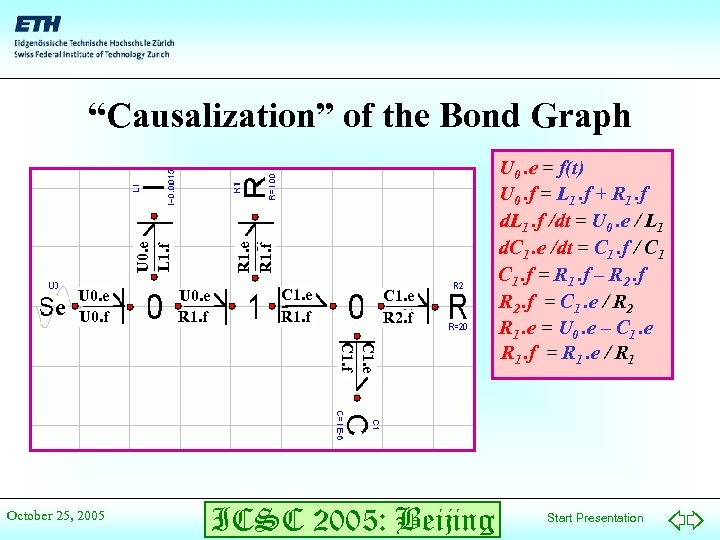
e U 0. f R 1. e R 1. f L 1. e U 0. e L 1. f “Causalization” of the Bond Graph U 0. e R 1. f C 1. e R 1. f R 2. e C 1. e R 2. f C 1. e C 1. f October 25, 2005 ICSC 2005: Beijing U 0. e = f(t) U 0. f = L 1. f + R 1. f d. L 1. f /dt = U 0. e / L 1 d. C 1. e /dt = C 1. f / C 1. f = R 1. f – R 2. f = C 1. e / R 2 R 1. e = U 0. e – C 1. e R 1. f = R 1. e / R 1 Start Presentation

The Four Base Variables of the Bond Graph Methodology • Beside from the two adjugate variables e and f, there are two additional physical quantities that play an important role in the bond graph methodology: Generalized Momentum: p = e · dt Generalized Position: q = f · dt October 25, 2005 ICSC 2005: Beijing Start Presentation

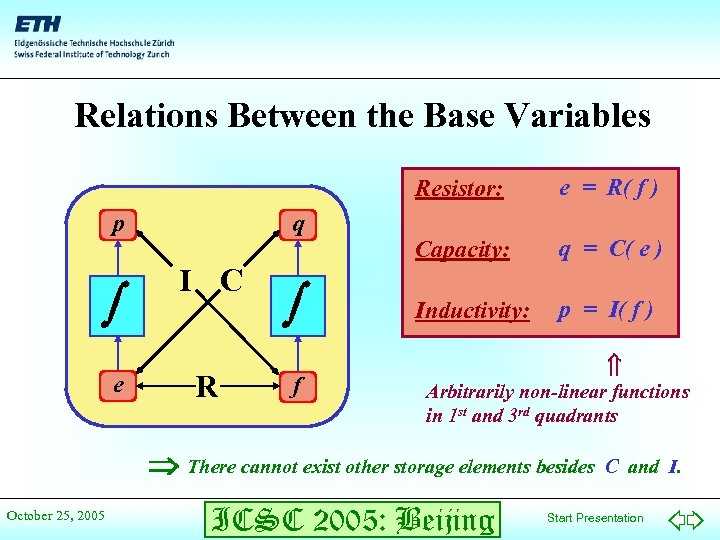
Relations Between the Base Variables Resistor: p e q I C R f e = R( f ) Capacity: q = C( e ) Inductivity: p = I( f ) Arbitrarily non-linear functions in 1 st and 3 rd quadrants There cannot exist other storage elements besides October 25, 2005 ICSC 2005: Beijing C and I. Start Presentation

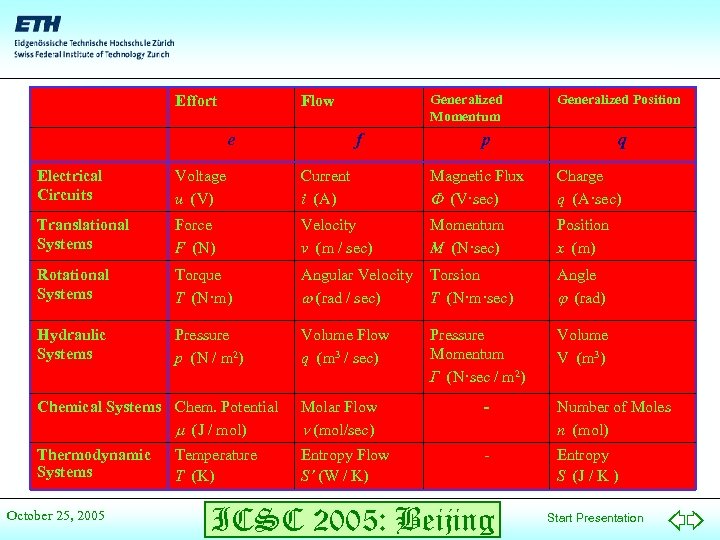
Effort Generalized Momentum Flow e f Generalized Position p q Electrical Circuits Voltage u (V) Current i (A) Magnetic Flux (V·sec) Charge q (A·sec) Translational Systems Force F (N) Velocity v (m / sec) Momentum M (N·sec) Position x (m) Rotational Systems Torque T (N·m) Angular Velocity (rad / sec) Torsion T (N·m·sec) Angle (rad) Hydraulic Systems Pressure p (N / m 2) Volume Flow q (m 3 / sec) Pressure Momentum Γ (N·sec / m 2) Volume V (m 3) Chemical Systems Chem. Potential (J / mol) Molar Flow (mol/sec) - Number of Moles n (mol) Thermodynamic Systems Entropy Flow S’ (W / K) - Entropy S (J / K ) October 25, 2005 Temperature T (K) ICSC 2005: Beijing Start Presentation

Hemodynamics • The hemodynamics describe the flow of blood through the heart and the blood vessels, i. e. , the flow of blood through the cardiovascular system. • The hemodynamics of the human body can be interpreted as a hydromechanical system. Blood is similar to water, blood vessels can be inerpreted as pipes, and the heart chambers act as hydraulic pumps. • Some of the chambers and vessels contain valves that act like check valves, preventing a backflow. October 25, 2005 ICSC 2005: Beijing Start Presentation

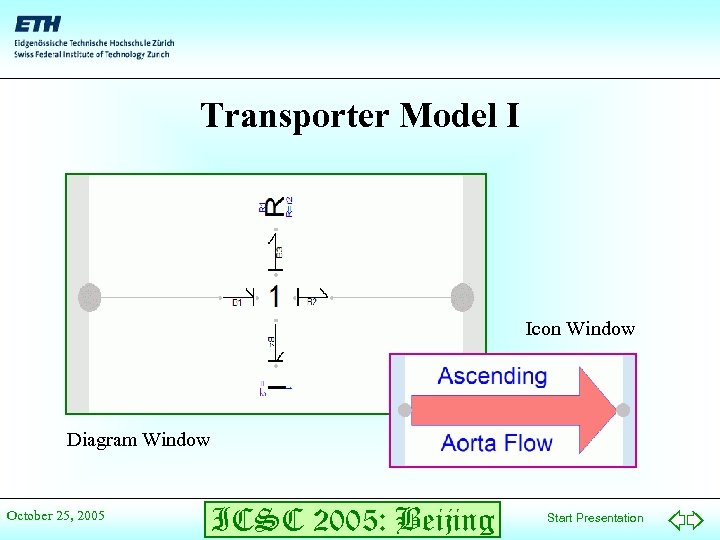
Transporter Model I Icon Window Diagram Window October 25, 2005 ICSC 2005: Beijing Start Presentation

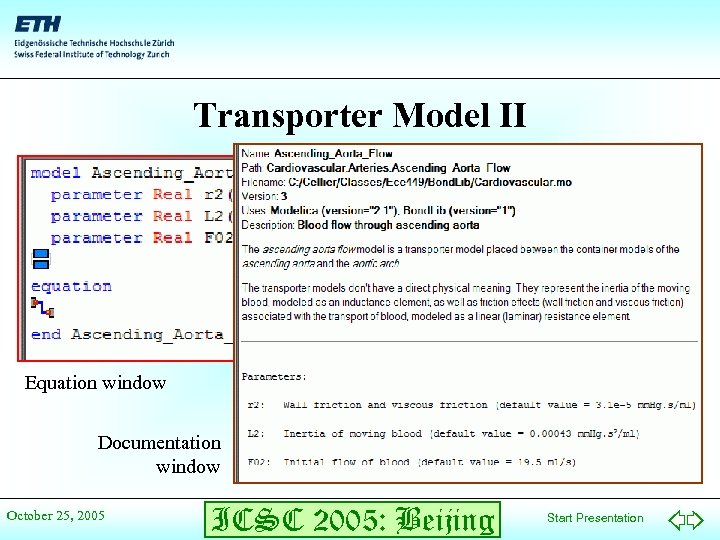
Transporter Model II Equation window Documentation window October 25, 2005 ICSC 2005: Beijing Start Presentation

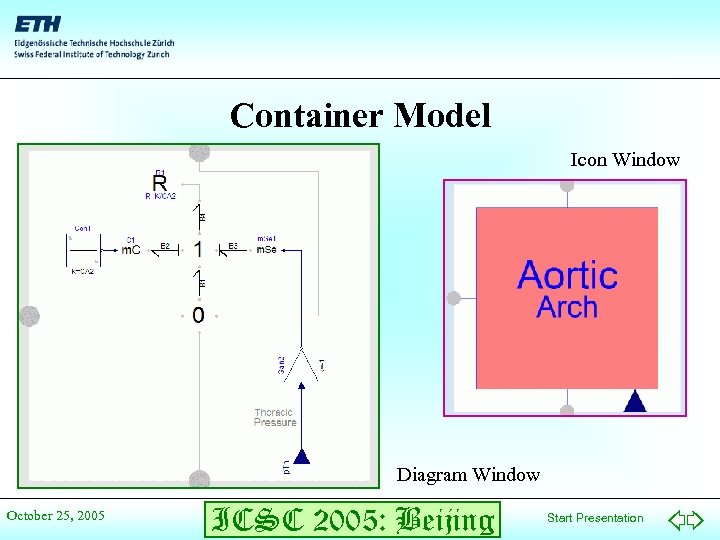
Container Model Icon Window Diagram Window October 25, 2005 ICSC 2005: Beijing Start Presentation

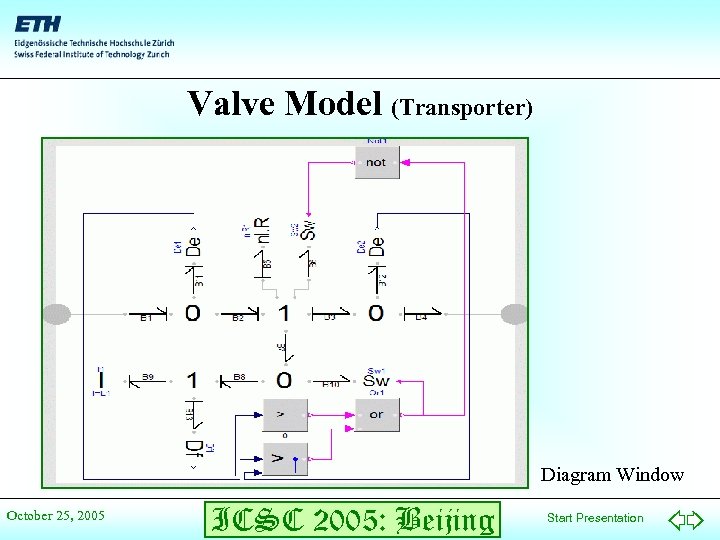
Valve Model (Transporter) Diagram Window October 25, 2005 ICSC 2005: Beijing Start Presentation

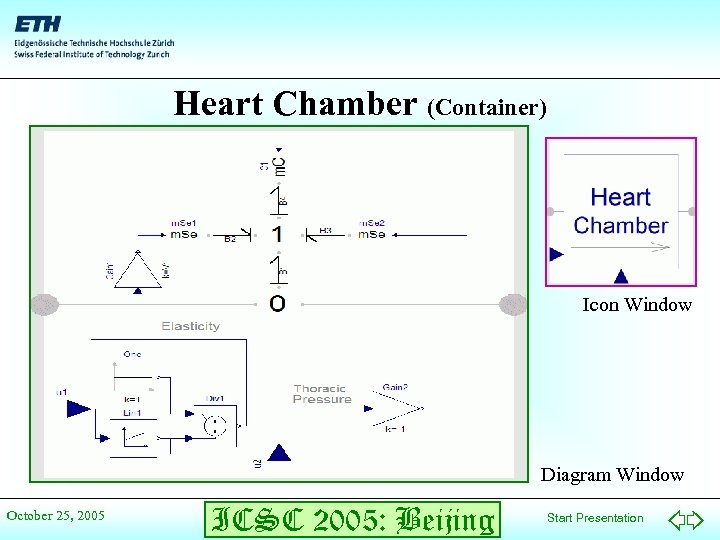
Heart Chamber (Container) Icon Window Diagram Window October 25, 2005 ICSC 2005: Beijing Start Presentation

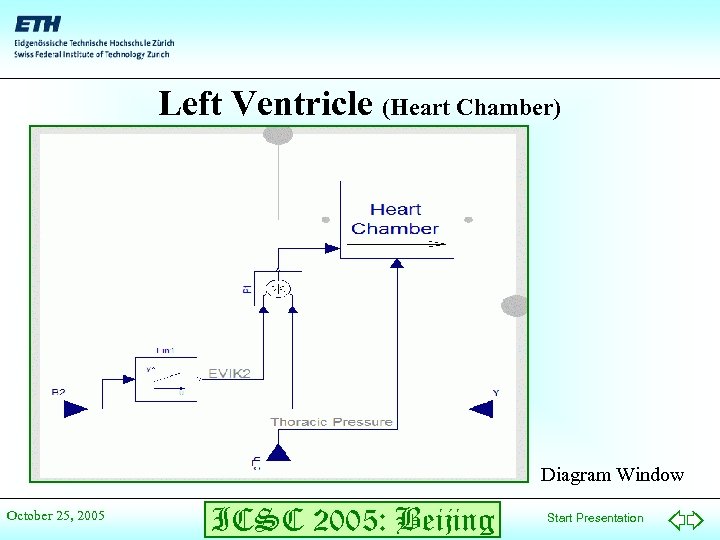
Left Ventricle (Heart Chamber) Diagram Window October 25, 2005 ICSC 2005: Beijing Start Presentation

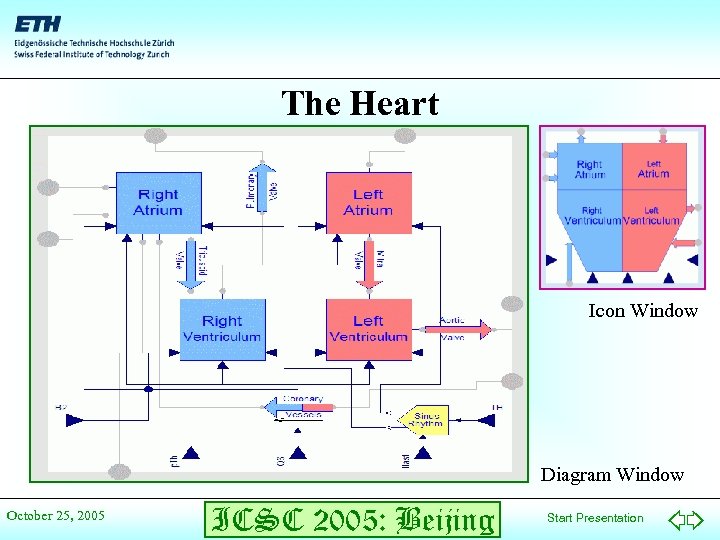
The Heart Icon Window Diagram Window October 25, 2005 ICSC 2005: Beijing Start Presentation

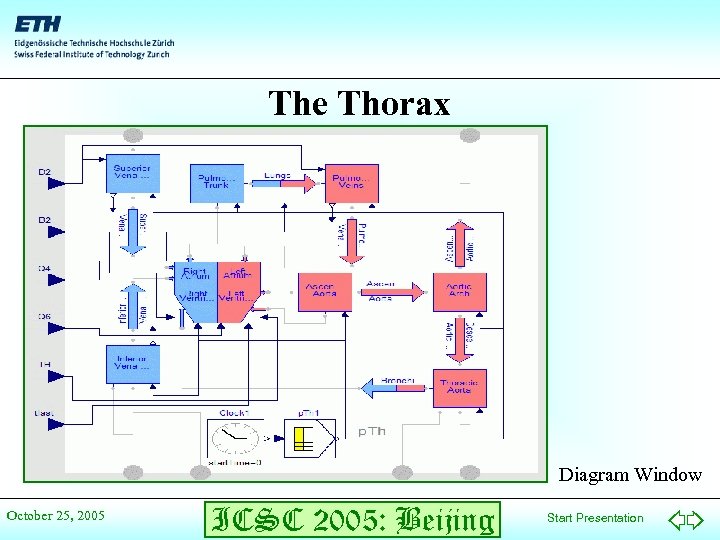
The Thorax Diagram Window October 25, 2005 ICSC 2005: Beijing Start Presentation

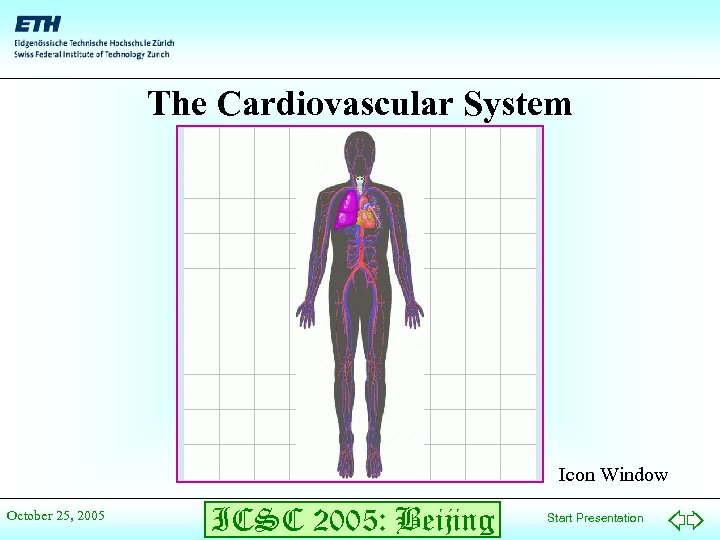
The Cardiovascular System Icon Window October 25, 2005 ICSC 2005: Beijing Start Presentation

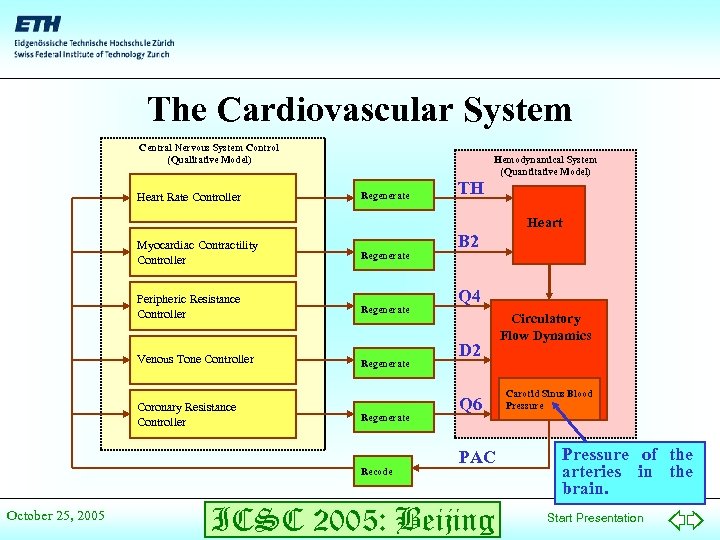
The Cardiovascular System Central Nervous System Control (Qualitative Model) Heart Rate Controller Hemodynamical System (Quantitative Model) Regenerate TH Heart Myocardiac Contractility Controller Regenerate Peripheric Resistance Controller Regenerate Venous Tone Controller Regenerate Coronary Resistance Controller Regenerate Recode October 25, 2005 B 2 Q 4 D 2 Q 6 PAC ICSC 2005: Beijing Circulatory Flow Dynamics Carotid Sinus Blood Pressure of the arteries in the brain. Start Presentation

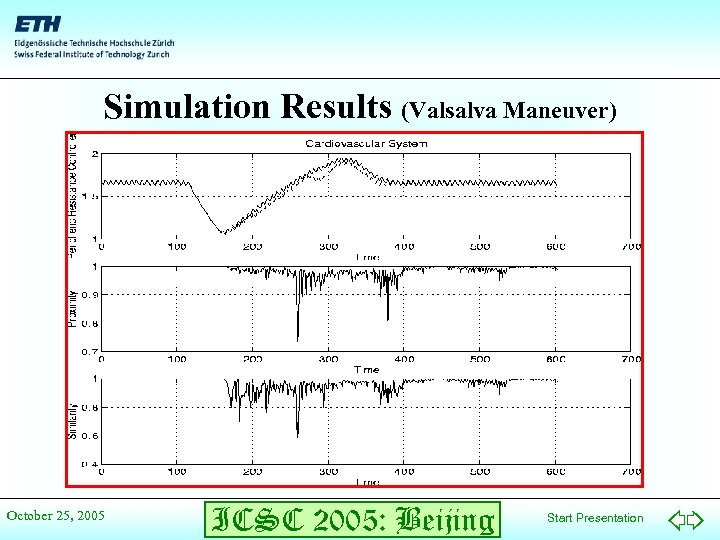
Simulation Results (Valsalva Maneuver) October 25, 2005 ICSC 2005: Beijing Start Presentation

Summary • Object-oriented graphical modeling has helped us translate a hydro-mechanical model of the cardiovascular system into a representation that medical personnel can interpret and deal with. • The knowledge at each layer was suitably encapsulated for limiting the local complexity to a level that can be represented on a single screen. • No manual translation from the high-level representation to executable simulation code is needed. The graphical model at each level contains all of the model equations at that level and underneath it. Hence the model can be compiled in a fully automated fashion and simulated thereafter. October 25, 2005 ICSC 2005: Beijing Start Presentation