Обертальний_рух_методичка_презентац.ppt
- Количество слайдов: 67

ОБЕРТАЛЬНИЙ РУХ ТВЕРДОГО ТІЛА КІНЕТИЧНА ЕНЕРГІЯ ОБЕРТАЛЬНОГО РУХУ ТВЕРДОГО ТІЛА Випадки, що вимагають нескладного інтегрування 2 Усні вправи 4 КОРИСНА ТЕОРЕМА 5 Усні вправи 6 Момент інерції кулі 7 Усні вправи 8 ТЕОРЕМА ГЮЙГЕНСА-ШТЕЙНЕРА 9 10 Усні вправи 11 ТЕНЗОР ІНЕРЦІЇ ТА ЕЛІПСОЇД ІНЕРЦІЇ 12 13 14 15 16 17 3 1
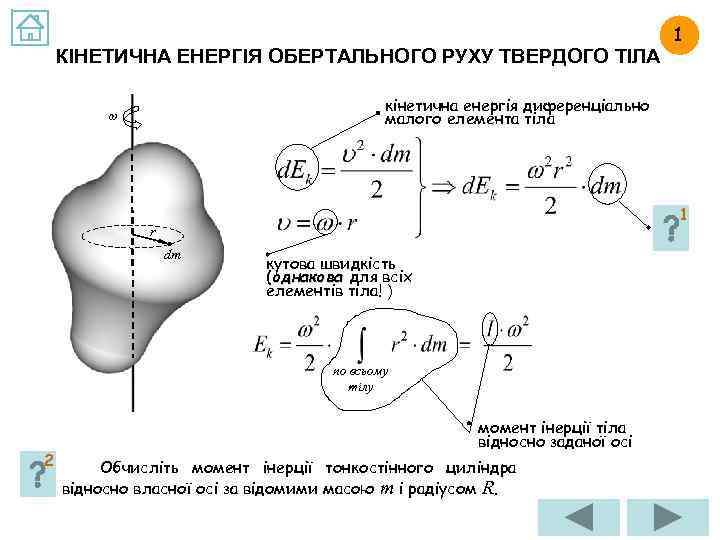
КІНЕТИЧНА ЕНЕРГІЯ ОБЕРТАЛЬНОГО РУХУ ТВЕРДОГО ТІЛА кінетична енергія диференціально малого елемента тіла ω ? r dm кутова швидкість (однакова для всіх елементів тіла! ) по всьому тілу 2 1 момент інерції тіла відносно заданої осі Обчисліть момент інерції тонкостінного циліндра відносно власної осі за відомими масою m і радіусом R. 1
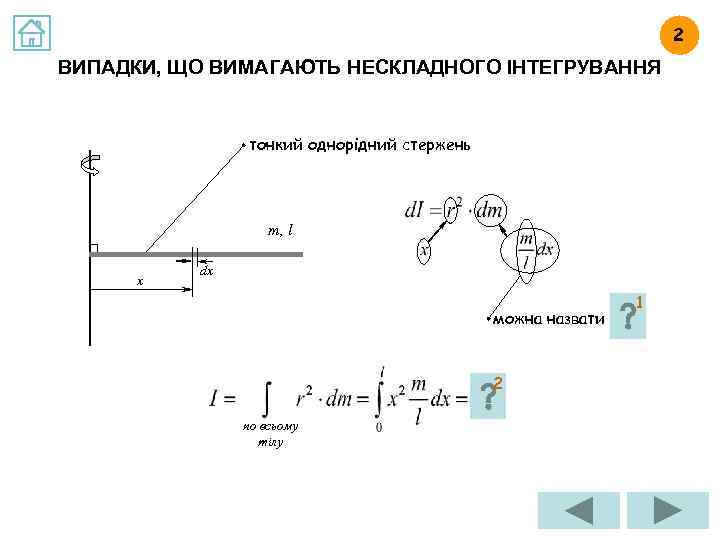
2 ВИПАДКИ, ЩО ВИМАГАЮТЬ НЕСКЛАДНОГО ІНТЕГРУВАННЯ тонкий однорідний стержень m, l x dx можна назвати 2 по всьому тілу 1
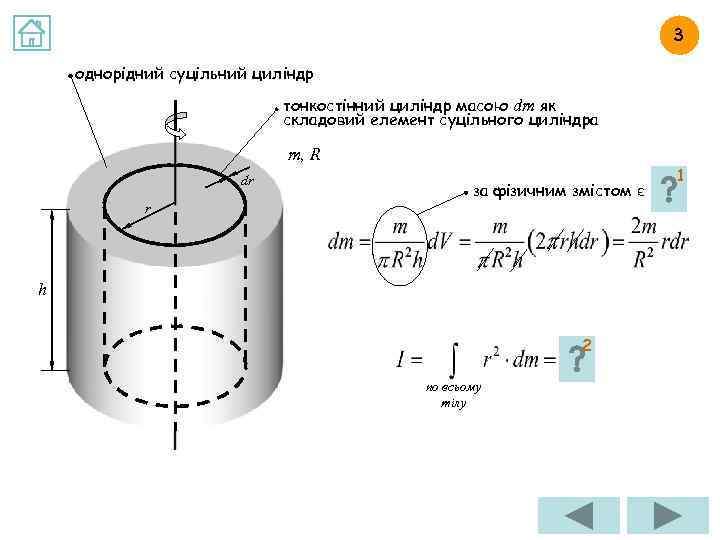
3 однорідний суцільний циліндр тонкостінний циліндр масою dm як складовий елемент суцільного циліндра m, R dr за фізичним змістом є r h 2 по всьому тілу 1
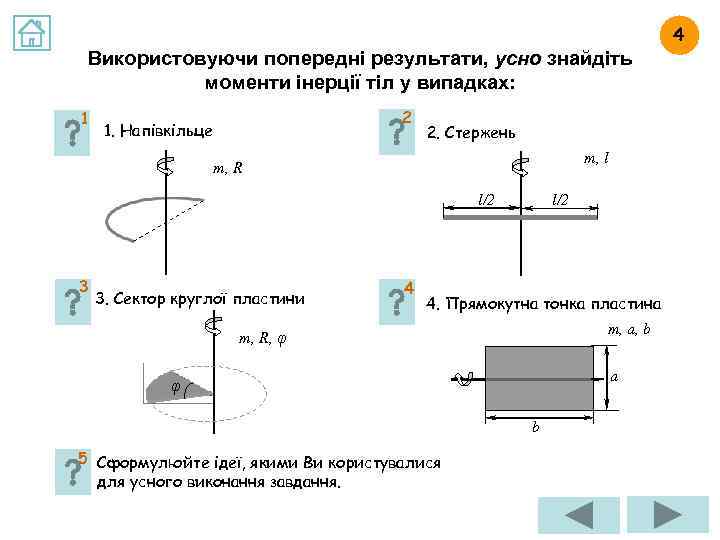
4 Використовуючи попередні результати, усно знайдіть моменти інерції тіл у випадках: 1 2 1. Напівкільце 2. Стержень m, l m, R l/2 3 3. Сектор круглої пластини 4 l/2 4. Прямокутна тонка пластина m, a, b m, R, φ a φ b 5 Сформулюйте ідеї, якими Ви користувалися для усного виконання завдання.

5 КОРИСНА ТЕОРЕМА момент інерції відносно точки перетину координатних осей моменти інерції відносно координатних осей по всьому тілу фізичного змісту не має, але допомагає у розрахунках! квадрат відстані до початку координат Момент інерції тонкостінної сфери відносно осі, що проходить через її центр z m, R (симетрія!) використовуючи теорему y x 2 Доведіть теорему. 1
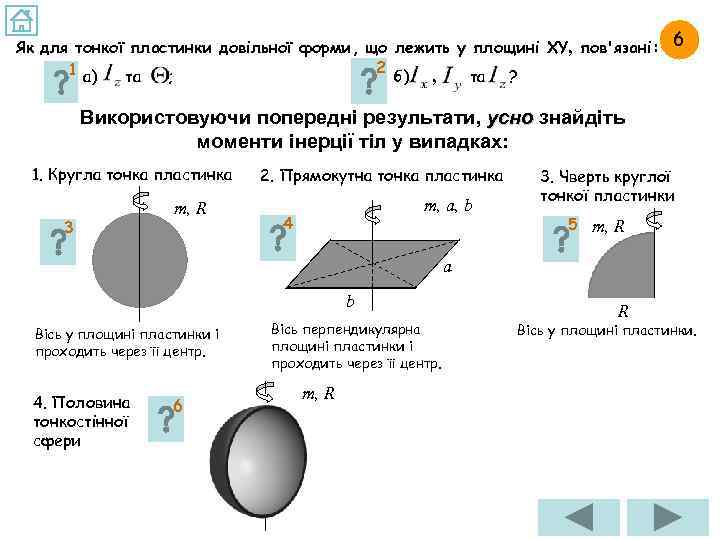
Як для тонкої пластинки довільної форми, що лежить у площині XY, пов'язані: 6 2 1 а) та ; б) , та ? Використовуючи попередні результати, усно знайдіть моменти інерції тіл у випадках: 1. Кругла тонка пластинка 3 m, R 2. Прямокутна тонка пластинка m, a, b 4 3. Чверть круглої тонкої пластинки 5 m, R a b Вісь у площині пластинки і проходить через її центр. 4. Половина тонкостінної сфери 6 Вісь перпендикулярна площині пластинки і проходить через її центр. m, R R Вісь у площині пластинки.
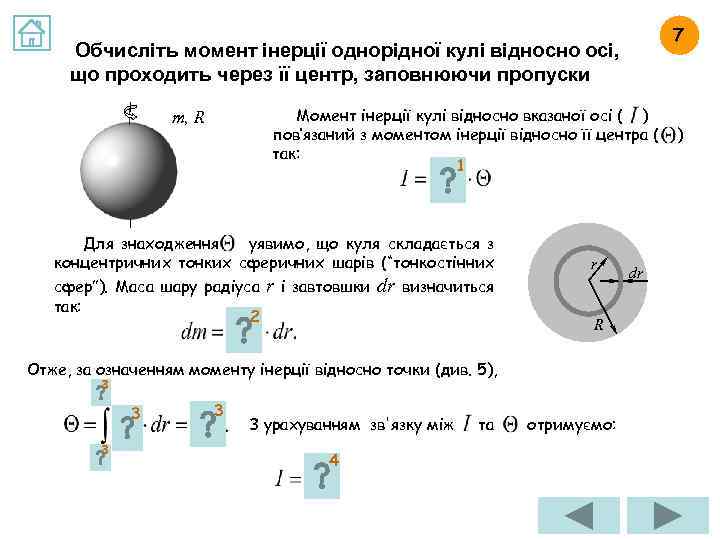
7 Обчисліть момент інерції однорідної кулі відносно осі, що проходить через її центр, заповнюючи пропуски Момент інерції кулі відносно вказаної осі ( ) пов’язаний з моментом інерції відносно її центра ( так: 1 m, R Для знаходження уявимо, що куля складається з концентричних тонких сферичних шарів (“тонкостінних сфер”). Маса шару радіуса r і завтовшки dr визначиться так: 2 r R Отже, за означенням моменту інерції відносно точки (див. 5), 3 3 З урахуванням зв'язку між 4 та отримуємо: dr )
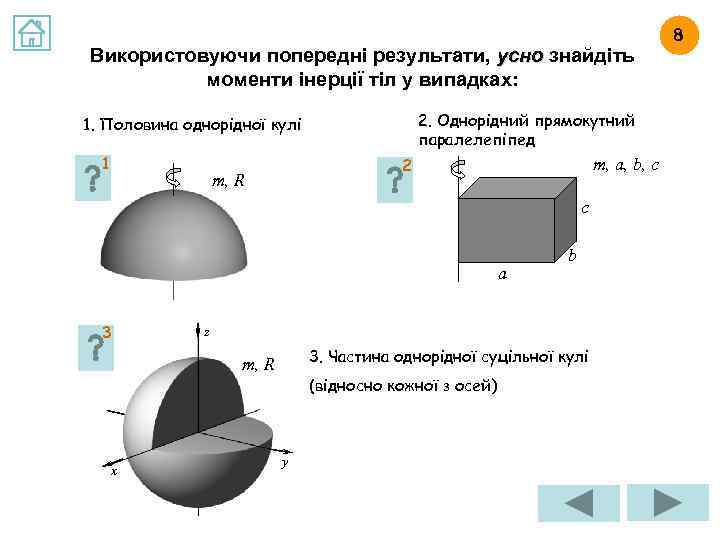
Використовуючи попередні результати, усно знайдіть моменти інерції тіл у випадках: 2. Однорідний прямокутний паралелепіпед 1. Половина однорідної кулі 1 2 m, R m, a, b, c c a 3 z 3. Частина однорідної суцільної кулі m, R x b (відносно кожної з осей) y 8
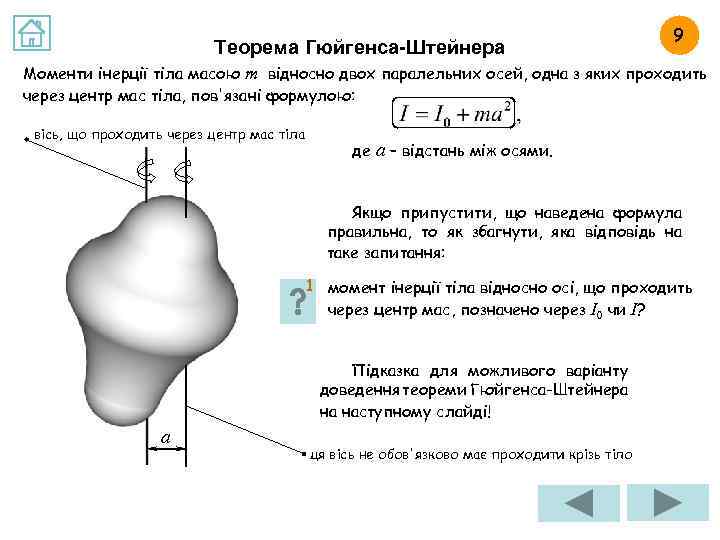
Теорема Гюйгенса-Штейнера 9 Моменти інерції тіла масою m відносно двох паралельних осей, одна з яких проходить через центр мас тіла, пов'язані формулою: вісь, що проходить через центр мас тіла де а – відстань між осями. Якщо припустити, що наведена формула правильна, то як збагнути, яка відповідь на таке запитання: 1 момент інерції тіла відносно осі, що проходить через центр мас, позначено через І0 чи І? Підказка для можливого варіанту доведення теореми Гюйгенса-Штейнера на наступному слайді! а ця вісь не обов'язково має проходити крізь тіло

10 Підказка для можливого варіанту доведення теореми Гюйгенса-Штейнера Розташуємо систему координат так, щоб її початок співпадав з центром мас тіла, а ми цікавилися моментами інерції відносно осі Z та осі, яка паралельна до неї. Нехай вісь, яка паралельна осі Z, перетинає площину XY у точці А (x. A, y. A, 0) так, що. , а Тоді по всьому тілу Врахуйте під час доведення, що 1 2 по всьому тілу Звідки взялося останнє твердження, яке рекомендовано врахувати? Продовжіть доведення самостійно!
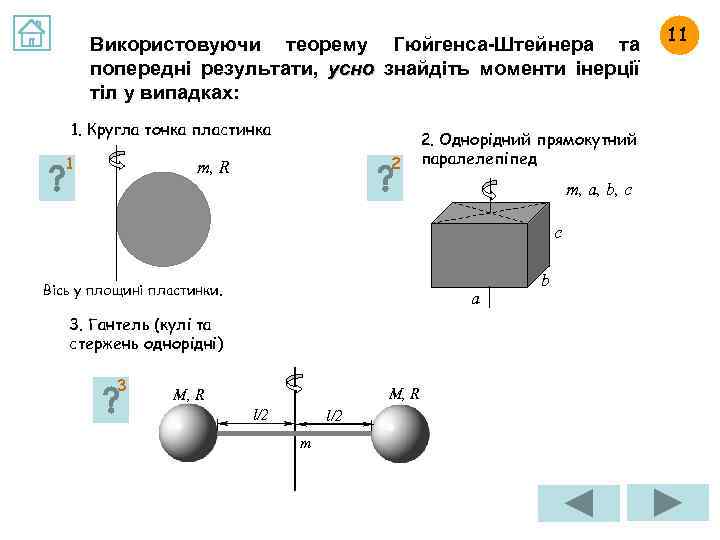
Використовуючи теорему Гюйгенса-Штейнера та попередні результати, усно знайдіть моменти інерції тіл у випадках: 1. Кругла тонка пластинка 1 2 m, R 2. Однорідний прямокутний паралелепіпед m, a, b, c c Вісь у площині пластинки. a 3. Гантель (кулі та стержень однорідні) 3 M, R l/2 m b 11

МОМЕНТ ІНЕРЦІЇ ТІЛА ВІДНОСНО ОСІ, ЩО ПРОХОДИТЬ ЧЕРЕЗ ПОЧАТОК 12 КООРДИНАТ, А ЇЇ НАПРЯМОК ЗАДАЄТЬСЯ ОДИНИЧНИМ ВЕКТОРОМ за означенням моменту інерції відносно осі див. рис. У прямокутній декартовій системі координат, використовуючи x 1, x 2, x 3 замість звичних x, y, z, а також відповідні позначення для проекцій , отримуємо: 1 радіус-вектор ; скалярний добуток векторів одиничний вектор, який задає напрямок осі (орт) З урахуванням співвідношення шуканий момент інерції можна подати у такому вигляд 2 Отримайте вирази для у вигляді інтегралів типу інтегрування ведеться по всьому тілу. 3 Доведіть, що загальний вираз для де — символ Кронекера. можна записати у вигляді де

ТЕНЗОР ІНЕРЦІЇ 13 Скорочений запис виразу для моменту інерції тіла відносно осі, що проходить через початок координат, а напрямок якої задається ортом , має вигляд: ^ , де ^ тензор інерції тіла відносно початку координат, який може бути поданий у вигляді симетричної матриці 3 3. У більш розгорнутому вигляді, знайомому з курсу лінійної алгебри, матимемо: 1 З урахуванням симетричності матриці тензора інерції перевірте, що такий запис для відповідає наведеному на попередньому основному слайді.

14 ЕЛІПСОЇД ІНЕРЦІЇ Формула для моменту інерції може отримати наочну геометричну інтерпретацію, якщо її порівняти з формулою для поверхні другого порядку 1 Доведіть, що “відстань” від початку координат до точки, на положення якої на цій поверхні вказує орт (тобто ), буде дорівнювати 2 Доведіть, що поверхня, про яку йшлося, є еліпсоїдом, центр якого співпадає з еліпсоїдом початком координат. Якщо систему координат повернути так, щоб її осі йшли вздовж головних осей еліпсоїда, то матриця, яка представляє тензор інерції тіла, набуде діагонального вигляду. 3 Користуючись поняттям еліпсоїда інерції та міркуваннями симетрії, обчисліть момент інерції тонкої круглої пластини (m, R) відносно осі, що проходить через її центр і утворює кут з нормаллю до площини пластини.

КІНЕТИЧНА ЕНЕРГІЯ І МОМЕНТ ІМПУЛЬСУ ТВЕРДОГО ТІЛА, ЩО ОБЕРТАЄТЬСЯ НАВКОЛО НЕРУХОМОЇ ОСІ 15 Якщо вісь обертання проходить через початок координат, а її напрямок задається одиничним вектором , що співпадає за напрямком з кутовою швидкістю , то скорочений запис виразу для кінетичної енергії має вигляд: ^ 1 Доведіть це твердження, згадавши, що ^ За означенням момент імпульсу тіла відносно початку координат визначається формулою: де а векторний добуток Примітка: інтегрування ведеться по всьому тілу. 2 Згадавши вираз для елементів тензора інерції і скориставшись формулою для подвійного векторного добутку (“бац мінус цаб”) доведіть, що ^

ГОЛОВНІ ОСІ ТА ГОЛОВНІ МОМЕНТИ ІНЕРЦІЇ Тензор інерції характеризує розподіл мас тіла по відношенню до фіксованої точки простору. Матриця, яка його представляє у декартовій системі координат з початком у цій точці, набуває діагонального вигляду, якщо осі координат спрямовані за головними осями відповідного еліпсоїда інерції. Моменти інерції тіла відносно цих осей і самі осі інерції називають головними для даної точки. Якщо ж ця точка є центром мас тіла, то — головними центральними 1 Які елементи матриці, що представляє тензор інерції тіла у даній декартовій системі координат, будуть дорівнювати нулю, якщо з трьох осей координат лише OZ співпадає з головною віссю інерції тіла для точки О? Доведіть такі корисні твердження: 2 Головна вісь інерції залишається головною для всіх своїх точок тоді і лише тоді, коли вона є головною центральною віссю інерції цього тіла. 3 Якщо у тіла є вісь матеріальної симетрії, то вона є головною центральною віссю інерції цього тіла. 4 Якщо у тіла є площина матеріальної симетрії, то будь-яка пряма, яка перпендикулярна цій площині, є головною віссю для точки, де ця пряма перетинає площину матеріальної симетрії. 16

ДЕКІЛЬКА КОНТРОЛЬНИХ ЗАПИТАНЬ, ПОВ ЯЗАНИХ З ТЕНЗОРОМ ІНЕРЦІЇ 1 Які максимальне і мінімальне значення моменту інерції однорідного куба маси m з довжиною ребра а відносно осі, що проходить через його вершину? 2 При якому співвідношенні між висотою і діаметром однорідного циліндра його момент інерції відносно осі, що проходить через центр мас, не залежатиме від її напрямку? 3 При якому куті між віссю кругового однорідного конуса і його твірною еліпсоїд інерції з центром у вершині конуса виродиться у сферу? 4 Яка необхідна і достатня умова того, щоб момент імпульсу тіла, що обертається навколо нерухомої осі, обчислений відносно будь-якої точки на осі обертання, співпадав за напрямком з вектором кутової швидкості? 17
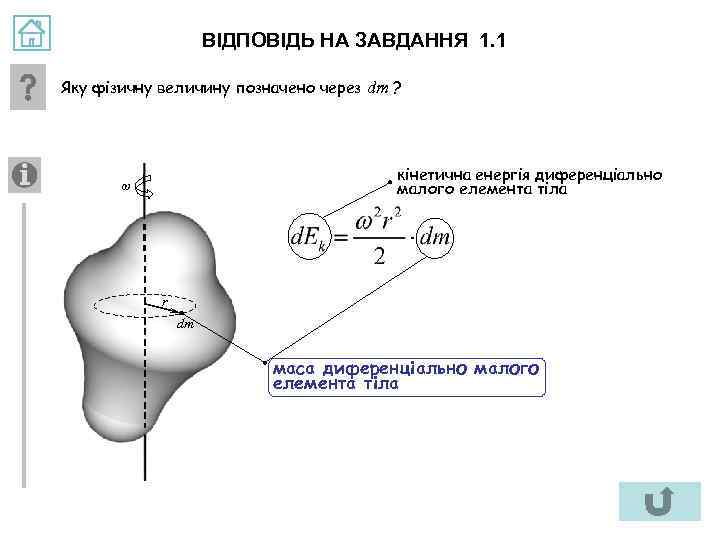
ВІДПОВІДЬ НА ЗАВДАННЯ 1. 1 Яку фізичну величину позначено через dm ? кінетична енергія диференціально малого елемента тіла ω r dm маса диференціально малого елемента тіла

ВІДПОВІДЬ НА ЗАВДАННЯ 1. 2 Обчисліть момент інерції тонкостінного циліндра відносно власної осі за відомими масою m і радіусом R. Відстань від будь-якого диференціально малого елемента тонкостінного циліндра до заданої осі однакова і дорівнює R (див. рис. ). Отже, Або, використовуючи формулу-означення, по всьому тілу
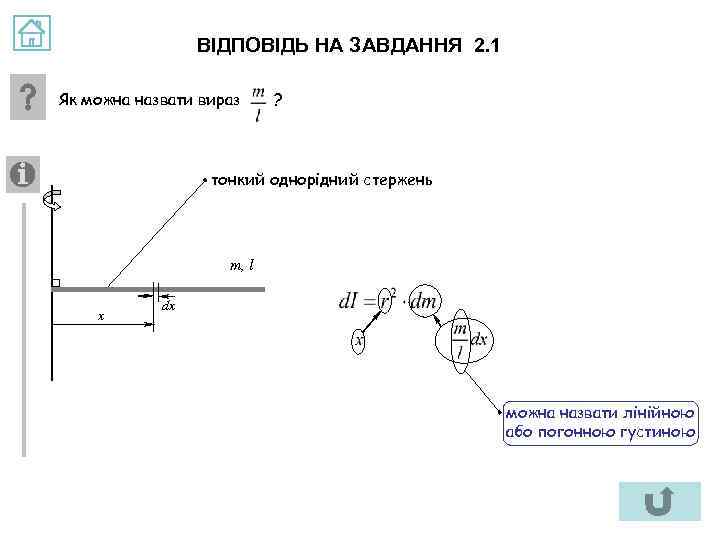
ВІДПОВІДЬ НА ЗАВДАННЯ 2. 1 Як можна назвати вираз ? тонкий однорідний стержень m, l x dx можна назвати лінійною або погонною густиною

ВІДПОВІДЬ НА ЗАВДАННЯ 2. 2 Продовжіть обчислення: тонкий однорідний стержень m, l x dx
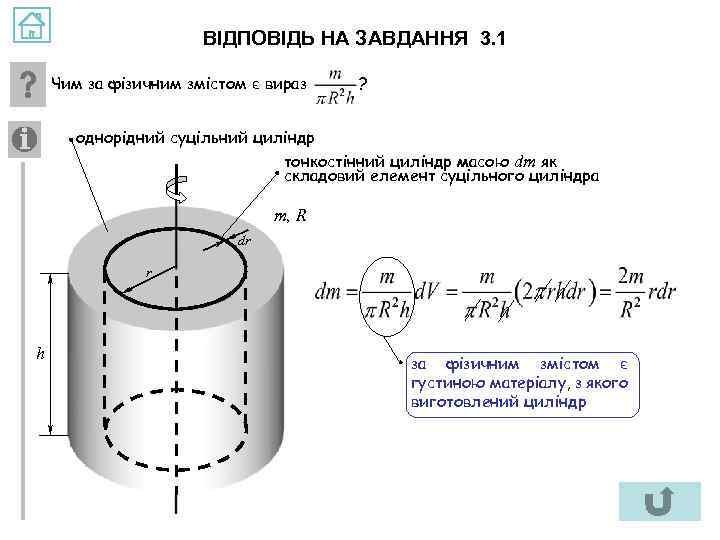
ВІДПОВІДЬ НА ЗАВДАННЯ 3. 1 Чим за фізичним змістом є вираз ? однорідний суцільний циліндр тонкостінний циліндр масою dm як складовий елемент суцільного циліндра m, R dr r h за фізичним змістом є густиною матеріалу, з якого виготовлений циліндр

ВІДПОВІДЬ НА ЗАВДАННЯ 3. 2 Знайдіть момент інерції однорідного суцільного циліндра відносно власної осі. однорідний суцільний циліндр тонкостінний циліндр масою dm як складовий елемент суцільного циліндра m, R dr r h Від h не залежить!
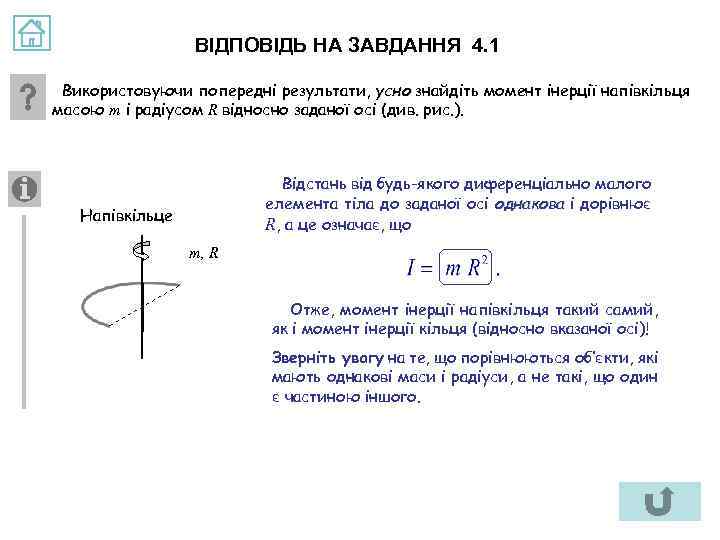
ВІДПОВІДЬ НА ЗАВДАННЯ 4. 1 Використовуючи попередні результати, усно знайдіть момент інерції напівкільця масою m і радіусом R відносно заданої осі (див. рис. ). Відстань від будь-якого диференціально малого елемента тіла до заданої осі однакова і дорівнює R, а це означає, що Напівкільце m, R Отже, момент інерції напівкільця такий самий, як і момент інерції кільця (відносно вказаної осі)! Зверніть увагу на те, що порівнюються об’єкти, які мають однакові маси і радіуси, а не такі, що один є частиною іншого.

ВІДПОВІДЬ НА ЗАВДАННЯ 4. 2 Використовуючи попередні результати, усно знайдіть момент інерції стержня масою m і довжиною l відносно заданої осі (див. рис. ). Стержень m, l l/2 m, l/2 Уявіть, що стержень розламали посередині і склали обидві половини разом так, як показано на нижньому рисунку. Така “перебудова” тіла не змінить моменту інерції. Це стає особливо зрозумілим, якщо уявити, що ліву половину стержня переміщують не паралельним переносом, а обертаючи навколо вказаної осі. При цьому відстань від кожного диференціально малого елемента тіла до осі обертання не буде змінюватися! А цей випадок уже був розібраний раніше (дивись відповідь на запитання 2. 2 — момент інерції стержня відносно перпендикулярної осі, що проходить через один з його кінців). Лише треба виконати заміну l/2 Остаточно отримуємо:

ВІДПОВІДЬ НА ЗАВДАННЯ 4. 3 Використовуючи попередні результати, усно знайдіть момент інерції сектора круглої пластинки масою m, радіусом R і кутом φ відносно заданої осі (див. рис. ). Сектор круглої пластини m, R, φ φ Уявіть, що речовину, з якої виготовлений сектор, “розподіляють” так, щоб утворити круглу пластину, але тоншу за ту, з якої був вирізаний сектор, причому всі диференціально малі елементи тіла переміщують по колу, не змінюючи відстані до осі обертання. Момент інерції відносно вказаної осі при цьому не зміниться! Отже, момент інерції сектора такий самий, як і момент інерції пластини або суцільного циліндра (відносно вказаної осі)! Зверніть увагу, що порівнюються об’єкти, які мають однакові маси і радіуси, а не такі, що один є частиною іншого.

ВІДПОВІДЬ НА ЗАВДАННЯ 4. 4 Використовуючи попередні результати, усно знайдіть момент інерції прямокутної тонкої пластинки масою m і розмірами axb відносно заданої осі (див. рис. ). Прямокутна тонка пластина m, a, b a b Уявіть, що речовину пластинки “стискають” так, щоб усі диференціально малі елементи тіла перемістилися паралельно осі обертання і утворили стержень (див. рис. ). Оскільки при цьому відстань від кожного елемента до осі обертання не змінюється, момент інерції тіла залишається такий самий! Отже, як і момент інерції стержня довжиною а відносно перпендикулярної до нього осі, що проходить через центр мас (дивись відповідь на завдання 4. 2), шуканий момент інерції пластини буде дорівнювати m, a a Від довжини сторони, що паралельна осі обертання, відповідь не залежить!

ВІДПОВІДЬ НА ЗАВДАННЯ 4. 5 Сформулюйте ідеї, якими Ви користувалися для усного виконання завдання. Головну ідею можна сформулювати так: якщо диференціально малий елемент тіла перемістити, не змінюючи відстані до осі обертання, то його “внесок” у загальний момент інерції всього тіла не зміниться. Отож, момент інерції напівкільця такий самий, як і момент інерції кільця; момент інерції сектора такий самий, як і момент інерції круга. Зрозуміло, що тут порівнюються об’єкти, що мають однакові маси і радіуси, а не такі, що один є частиною іншого! Тією ж ідеєю ми скористалися і у випадках стержня та пластини.

ВІДПОВІДЬ НА ЗАВДАННЯ 5. 1 Знайдіть момент інерції тонкостінної сфери масою m і радіусом R відносно осі, що проходить через її центр. z m, R (симетрія!) x y використовуючи теорему Отже,

ВІДПОВІДЬ НА ЗАВДАННЯ 5. 2 Доведіть теорему. ДОВЕДЕННЯ КОРИСНОЇ ТЕОРЕМИ z dm (x, y, z) y x після інтегрування по всьому тілу отримуємо:

ВІДПОВІДЬ НА ЗАВДАННЯ 6. 1 Як для тонкої пластинки довільної форми, що лежить у площині XY, пов'язані та ? Якщо пластина лежить у площині ХY, то z-координати всіх матеріальних точок дорівнюють нулю, а тому момент інерції Θ пластинки відносно початку координат буде мати вигляд по всьому тілу тобто буде дорівнювати моменту інерції пластинки відносно осі Z. Таким чином, у випадку площинного розподілу мас

ВІДПОВІДЬ НА ЗАВДАННЯ 6. 2 Як для тонкої пластинки довільної форми, що лежить у площині XY, пов'язані , та ? Якщо пластина лежить у площині ХY, то z-координати всіх матеріальних точок дорівнюють нулю, а тому момент інерції Θ пластинки відносно початку координат буде дорівнювати моменту інерції пластинки відносно осі Z (дивись відповідь на завдання 6. 1), з іншого боку, (див. відповідь на завдання 5. 2 — корисна теорема). Відповідно, у випадку площинного розподілу мас

ВІДПОВІДЬ НА ЗАВДАННЯ 6. 3 Використовуючи попередні результати, усно знайдіть момент інерції круглої тонкої пластинки масою m і радіусом R відносно заданої осі (див. рис. ). Кругла тонка пластинка m, R у х Скористаємось формулою, отриманою для випадку площинного розподілу мас (дивись відповідь на завдання 6. 2): Якщо позначити осі Х та Y так, як показано на рисунку, то вісь Z буде перпендикулярна до площини пластини. Моменти інерції Іх та Іу будуть однаковими, тобто Вісь у площині пластинки і проходить через її центр. А момент інерції Іz круглої тонкої пластини буде таким самим, як і момент інерції суцільного циліндра відносно його осі (дивись відповідь на завдання 3. 2): Отже,

ВІДПОВІДЬ НА ЗАВДАННЯ 6. 4 Використовуючи попередні результати, усно знайдіть момент інерції прямокутної тонкої пластини масою m і розмірами axb відносно заданої осі (див. рис. ). Прямокутна тонка пластина z m, a, b a х b у Позначимо вісь обертання як вісь Z, а осі оберемо так, як показано на рисунку. Х та Y Далі скористаємось отриманими формулами для випадку площинного розподілу мас: (дивись відповідь на завдання 6. 2), (див відповідь на завдання 4. 4). У результаті матимемо:

ВІДПОВІДЬ НА ЗАВДАННЯ 6. 5 Використовуючи попередні результати, усно знайдіть момент інерції чверті круглої тонкої пластинки масою m і радіусом R відносно заданої осі (див. рис. ). Чверть круглої тонкої пластинки m, R R Якщо застосувати ідею про перенесення диференціально малих мас тіла, то можна дійти висновку, що момент інерції чверті круглої пластини дорівнює моменту інерції цілої пластини з такими самими R та m: Дійсно, якщо кожний з диференціально малих елементів поділити на чотири рівних за масою частини, а потім, залишивши одну з них на своєму місці, три інші перемістити так, як показано на рисунку, то отримаємо цілу пластинку з тим самим моментом інерції, бо відповідні відстані до осі обертання не зміняться.

ВІДПОВІДЬ НА ЗАВДАННЯ 6. 6 Використовуючи попередні результати, усно знайдіть момент інерції половини тонкостінної сфери масою m і радіусом R відносно заданої осі (див. рис. ). Половина тонкостінної сфери m, R Застосуємо ідею про перенесення диференціально малих елементів тіла, отримавши з половини сфери цілу сферу з такими ж масою і радіусом. Для цього кожен елемент тіла поділимо на дві рівних за масою частини, а потім, залишивши одну на своєму місці, другу розмістимо у точці, яка розташована симетрично відносно осі обертання. Отже, момент інерції половини сфери дорівнює моменту інерції цілої сфери з такими самими масою і радіусом (дивись відповідь на завдання 5. 1):

ВІДПОВІДЬ НА ЗАВДАННЯ 7. 1 Як пов'язані між собою момент інерції кулі відносно вказаної осі ( момент інерції кулі відносно її центра ( )? )і Якщо скористатися корисною теоремою (див. 5. 2) m, R та міркуваннями симетрії: то можна дійти висновку, що момент інерції кулі відносно вказаної осі ( ) пов’язаний з моментом інерції відносно її центра ( ) так: Зауважимо, що такими ж міркуваннями ми користувалися, обчислюючи момент інерції тонкостінної сфери відносно осі, що проходить через її центр (див. відповідь на завдання 5. 1).

ВІДПОВІДЬ НА ЗАВДАННЯ 7. 2 Знайдіть dm — масу шару радіуса r і завтовшки dr. Маса тонкого сферичного шару радіуса завтовшки dr визначиться так: rі об'ємна густина матеріалу, з якого виготовлена куля r dr R (об'єм тонкого сферичного шару знаходиться як добуток площі сфери на товщину шару)

ВІДПОВІДЬ НА ЗАВДАННЯ 7. 3 Знайдіть момент інерції кулі відносно її центра. Зверніть увагу на те, що під час обчислення моменту інерції кулі відносно її центра диференціально малими елементами цієї кулі ми вважали тонкі сферичні шари, з яких складається куля (“тонкостінні сфери”, як іноді спрощено їх називають).

ВІДПОВІДЬ НА ЗАВДАННЯ 7. 4 Знайдіть момент інерції кулі відносно осі, що проходить через її центр. Для знаходження моменту інерції кулі відносно осі, що проходить через її центр, треба розв'язати таку систему рівнянь:

ВІДПОВІДЬ НА ЗАВДАННЯ 8. 1 Використовуючи попередні результати, усно знайдіть момент інерції половини однорідної кулі масою m і радіусом R відносно заданої осі (див. рис. ). Половина однорідної кулі m, R Якщо застосувати ідею про перенесення диференціально малих елементів тіла (паралельно осі), то можна зрозуміти, що момент інерції половини кулі дорівнює моменту інерції цілої кулі (з такими самими масою і радіусом, відносно вказаної осі): Подумайте над тим, які саме елементи і куди треба переносити, та спробуйте надати розгорнуті пояснення (на зразок тих, що наведені у відповідях на завдання 6. 5; 6. 6).

ВІДПОВІДЬ НА ЗАВДАННЯ 8. 2 Використовуючи попередні результати, усно знайдіть момент інерції однорідного прямокутного паралелепіпеда масою m і розмірами axbxc відносно заданої осі (див. рис. ). Момент інерції тіла не зміниться, якщо паралелепіпед “стиснути” у тонку прямокутну Однорідний прямокутний пластинку, що лежить у площині XY, якщо паралелепіпед m, a, b, c вважати вісь обертання віссю Z (висота паралелепіпеда не буде входити до відповіді!). c a b Тепер згадаємо співвідношення, яке має місце для будь-якої тонкої пластини, що лежить у площині XY: (дивись відповідь на завдання 6. 2). Моменти інерції пластини відносно осей Х і Y можна знайти “перетворивши” по черзі пластину у стержні з довжинами а і b. Використавши попередні результати (дивись відповідь на завдання 2. 2), отримаємо: Отже, відповідь:

ВІДПОВІДЬ НА ЗАВДАННЯ 8. 3 Використовуючи попередні результати, усно знайдіть момент інерції частини однорідної суцільної кулі масою m і радіусом R відносно кожної з осей (див. рис. ). Частина однорідної суцільної кулі (відносно кожної з осей) z m, R x Якщо знов застосувати ідею про перенесення диференціально малих елементів тіла, можна збагнути, що моменти інерції зображеної частини кулі відносно кожної із запропонованих осей дорівнюють моменту інерції цілої кулі з такими самими m і R (відносно осі, що проходить через центр кулі): y Подумайте над тим, які саме елементи і куди треба переносити у кожному з трьох випадків, та спробуйте надати розгорнуті пояснення (на зразок тих, що наведені у відповідях на завдання 6. 5; 6. 6).

ВІДПОВІДЬ НА ЗАВДАННЯ 9. 1 У теоремі Гюйгенса-Штейнера момент інерції тіла відносно осі, що проходить через центр мас, позначено через І0 чи І? вісь, що проходить через центр мас тіла Якщо взяти значення відстані між осями а набагато більшим, ніж максимальний лінійний розмір тіла, то значення моменту інерції відносно осі, що не проходить через центр мас, має прямувати до , бо тіло можна буде вважати матеріальною точкою. Зрозуміло, що такій вимозі у наведеній формулі задовольняє I, а не I 0. Отже, якщо формула правильна, то а момент інерції тіла відносно осі, що проходить через центр мас тіла, позначено через І0. ця вісь не обов'язково має проходити крізь тіло

ВІДПОВІДЬ НА ЗАВДАННЯ 10. 1 Звідки взялося твердження врахувати? , яке рекомендовано Це твердження пов'язано із формулою-визначенням радіус-вектора центра мас тіла : по всьому тілу Оскільки система координат була обрана так, щоб її початок співпадав з центром мас тіла, то по всьому тілу Останню векторну рівність можна переписати, як відомо, у вигляді трьох скалярних:

ВІДПОВІДЬ НА ЗАВДАННЯ 10. 2 Продовжіть доведення теореми Гюйгенса-Штейнера. Виконаємо деякі перетворення: по всьому тілу оскільки

ВІДПОВІДЬ НА ЗАВДАННЯ 11. 1 Використовуючи теорему Гюйгенса-Штейнера та попередні результати, усно знайдіть момент інерції круглої тонкої пластинки масою m і радіусом R відносно заданої осі (див. рис. ). Кругла тонка пластинка m, R Нагадаємо раніше отриманий результат для осі, що була у площині пластини і проходила через її центр (дивись відповідь на завдання 6. 3): m, R Вісь у площині пластинки. Використаємо теорему Гюйгенса-Штейнера:

ВІДПОВІДЬ НА ЗАВДАННЯ 11. 2 Використовуючи теорему Гюйгенса-Штейнера та попередні результати, усно знайдіть момент інерції однорідного прямокутного паралелепіпеда масою m і розмірами axbxc відносно заданої осі (див. рис. ). Однорідний прямокутний паралелепіпед Використаємо теорему Гюйгенса-Штейнера та раніше отриманий результат для осі, на якій лежить ребро паралелепіпеда (дивись відповідь на завдання 8. 2): m, a, b, c c c a b Якщо б не було вимоги обов'язково скористатися теоремою Гюйгенса-Штейнера, то можна було б “стиснути” паралелепіпед до тонкої прямокутної пластини і одразу записати відповідь (дивись відповідь на завдання 6. 4).

ВІДПОВІДЬ НА ЗАВДАННЯ 11. 3 Використовуючи теорему Гюйгенса-Штейнера та попередні результати, усно знайдіть момент інерції зображеної на рисунку гантелі відносно заданої осі. Гантель (кулі та стержень однорідні) M, R l/2 m Момент інерції є адитивною величиною. Отже, момент інерції гантелі дорівнює сумі моментів інерції двох куль та стержня. Використовуючи попередні результати (дивись відповіді на завдання 4. 2; 7. 4) та теорему Гюйгенса-Штейнера (для знаходження моменту інерції кулі відносно вказаної осі обертання), отримуємо:

ВІДПОВІДЬ НА ЗАВДАННЯ 12. 1 У прямокутній декартовій системі координат, використовуючи x 1, x 2, x 3 замість звичних x, y, z, а також враховуючи відповідні позначення для , отримуємо: ; скалярний добуток векторів Запишемо вирази для використовуючи і у прямокутній декартовій системі координат, замість і запропоновані позначення для координат: Враховуючи ортонормованість базису отримаємо вираз для тобто скалярний добуток двох векторів дорівнює сумі добутків їх відповідних координат. Відповідно,

ВІДПОВІДЬ НА ЗАВДАННЯ 12. 2 Отримайте вирази для у вигляді інтегралів типу Спочатку запишемо у потрібному для подальших перетворень вираз для врахувавши, що спеціально введений множник, який дорівнює одиниці Далі підставимо отриманий результат у формулу для моменту інерції тіла відносно осі: Отже,

ВІДПОВІДЬ НА ЗАВДАННЯ 12. 3 Доведіть, що загальний вираз для де можна записати у вигляді — символ Кронекера. За означенням, Із урахуванням цього запишемо вирази для та Порівнявши отримані вирази із наведеними на попередньому слайді, бачимо, що вони співпадають. Зрозуміло, що і для інших значень для можна записати у запропонованому вигляді. та загальний вираз

ВІДПОВІДЬ НА ЗАВДАННЯ 13. 1 Перевірте, що вираз для може бути поданий як ^ , наведений на попередньому основному слайді, Спочатку виконаємо множення матриці на стовпець: Тепер рядок помножимо на отриманий стовпець: Враховуючи симетричність тензора інерції запишемо кінцевий результат у потрібному вигляді: , спростимо останній вираз і

ВІДПОВІДЬ НА ЗАВДАННЯ 14. 1 Доведіть, що “відстань” на цій поверхні вказує орт від початку координат до точки, на положення якої (тобто Вираз для моменту інерції ), буде дорівнювати можна привести до потрібного вигляду поділивши обидві частини рівняння на Знайдемо шукану “відстань”: Зверніть увагу на розмірність “відстані”! і вводячи заміни:

ВІДПОВІДЬ НА ЗАВДАННЯ 14. 2 Доведіть, що поверхня, про яку йшлося, є еліпсоїдом, центр якого співпадає з еліпсоїдом початком координат. Як було доведено раніше, формулу для моменту інерції можна унаочнити за допомогою поверхні другого порядку: “Відстань” від початку координат до точки на цій поверхні Ця відстань обмежена. Серед поверхонь другого порядку обмежені лише еліпсоїди. Тобто наочною інтерпретацією тензора інерції є еліпсоїд інерції. У випадку наявності такого напрямку, для якого в циліндр. (уздовж тонкого стержня), еліпсоїд вироджується

ВІДПОВІДЬ НА ЗАВДАННЯ 14. 3 Користуючись поняттям еліпсоїда інерції та міркуваннями симетрії обчисліть момент інерції тонкої круглої пластини (m, R) відносно осі, що проходить через її центр і утворює кут з нормаллю до площини пластини. тонка кругла пластина (вигляд збоку) m, R Якщо початок координат обрати у центрі мас пластини, а вісь х3 спрямувати вздовж вектора нормалі, то моменти інерції відносно координатних осей буде нескладно знайти: Також зрозуміло, що для цієї пластини в обраній системі координат усі інші компоненти тензора Зазначимо, що інерції (відцентрові моменти) дорівнюватимуть (див. рис. ) називають напрямними косинусами, бо вони є косинусами кутів між вектором і ортами системи координат Якщо система координат обрана так, як показано на рисунку, то Отже, нулю. відповідно.

ВІДПОВІДЬ НА ЗАВДАННЯ 15. 1 Доведіть таке твердження: якщо вісь обертання проходить через початок координат, а її напрямок задається одиничним вектором , що співпадає за напрямком з , то скорочений запис виразу для кінетичної енергії має вигляд: ^ ^ Скористайтеся таким: Враховуючи наведені вище формули, отримуємо: ^ що і потрібно було довести. ^ ^

ВІДПОВІДЬ НА ЗАВДАННЯ 15. 2 Доведіть, що ^ згадавши вираз для елементів тензора інерції і скориставшись формулою для подвійного векторного добутку (“бац мінус цаб”). За означенням моменту імпульсу тіла відносно початку координат маємо: де Скористаємось формулою подвійного векторного добутку: Переходячи до координатного запису, отримуємо: А це означає, що ^

ВІДПОВІДЬ НА ЗАВДАННЯ 16. 1 Які елементи матриці, що представляє тензор інерції тіла у даній декартовій системі координат, будуть дорівнювати нулю, якщо з трьох осей координат лише OZ співпадає з головною віссю інерції тіла для точки О? Якщо вісь OZ є головною віссю інерції тіла для точки О, то поворотом навколо цієї осі можна перейти до системи координат, де матриця, що представляє тензор інерції, набуде діагонального вигляду, а рівняння еліпсоїда інерції запишеться так: причому 1 1 А як виразити координати і через і , можна зрозуміти з наведеного креслення. Дійсно, якщо вектор з координатами (1; 0) у системі XOY буде у системі X*OY* мати координати ( ), а з (0; 1) матиме ( ), то Після підстановки виразів для вання доданків отримаємо: і у рівняння еліпсоїда інерції і відповідного групу- Як бачимо, дорівнюють нулю такі елементи матриці:

ВІДПОВІДЬ НА ЗАВДАННЯ 16. 2 Доведіть таке корисне твердження: “Головна вісь інерції залишається головною для всіх своїх точок тоді і лише тоді, коли вона є головною центральною віссю інерції цього тіла”. Припустимо, що головною віссю інерції є вісь OZ. Оберемо довільну точку О' на осі OZ і проведемо через неї, паралельно осям ОХ та ОY, вісі О'Х' та О'Y'. Вісь O'Z' при цьому буде співпадати з віссю OZ (див. рис. ). З'ясуємо, за яких умов вісь O'Z' буде головною для точки О'. Z' Z Той факт, що вісь OZ є головною у “старій” системі координат означає, що у цій системі дорівнюють нулю (див. відповідь на завдання 16. 1). Нові координати точок тіла пов'язані зі ста. O' рими так: a O X' Y' Y Для цікавих для нас елементів “нової” матриці матимемо вирази: X Таким чином, якщо центр мас тіла буде належати осі OZ, то І навпаки: якщо то Отже, головна вісь інерції залишається головною для всіх своїх точок тоді і лише тоді, коли вона є головною центральною віссю інерції цього тіла.

ВІДПОВІДЬ НА ЗАВДАННЯ 16. 3 Доведіть таке корисне твердження: “Якщо у тіла є вісь матеріальної симетрії, то вона є головною центральною віссю інерції цього тіла”. Віссю матеріальної симетрії називають пряму, що має таку властивість: якщо з будь-якої точки масою mi провести пряму, перпендикулярну до цієї осі, то на продовженні цієї прямої обов'язково знайдеться інша точка з такою самою масою і розташована на такій самій відстані від осі. Тут точками названі диференціально малі елементи тіла, на які можна його умовно поділити. Тобто, якщо позначити вісь симетрії через OZ, то з властивостей матеріальної симетрії випливає, що для кожної і-ої точки тіла з координатами xi, yi, zi і масою mi можна знайти точку з такою самою масою mi і координатами -xi, -yi, zi. Це означає, що Ixz та Iyz будуть дорівнювати нулю, причому, незалежно від положення початку координат О на осі матеріальної симетрії. Отже, вісь матеріальної симетрії є головною центральною віссю інерції цього тіла (див. відповіді на завдання 16. 1, 16. 2).

ВІДПОВІДЬ НА ЗАВДАННЯ 16. 4 Доведіть таке корисне твердження: “Якщо у тіла є площина матеріальної симетрії, то будь-яка пряма, яка перпендикулярна цій площині, є головною віссю для точки, де ця пряма перетинає площину матеріальної симетрії”. Тіло має площину матеріальної симетрії, якщо для будь-якої і-ої точки масою mi можна знайти іншу точку з такою самою масою, що розташована на загальному перпендикулярі до площини, але з іншого боку від неї. Якщо позначити площину симетрії через ХOY, то для кожної і-ої точки тіла з координатами xi, yi, zi і масою mi можна знайти точку з такою самою масою mi і координатами xi, yi, -zi. Це означає, що Ixz та Iyz будуть дорівнювати нулю. Таким чином, якщо у тіла є площина матеріальної симетрії, то будь-яка пряма, яка перпендикулярна цій площині, є головною віссю для точки, де ця пряма перетинає площину матеріальної симетрії.

ВІДПОВІДЬ НА ЗАВДАННЯ 17. 1 Які максимальне і мінімальне значення моменту інерції однорідного куба маси m з довжиною ребра а відносно осі, що проходить через його вершину? Осі, що проходять через центри протилежних граней однорідного куба, безперечно є головними центральними осями інерції, бо вони є осями матеріальної симетрії (див. відповідь на завдання 16. 3). Моменти інерції куба відносно них однакові. Отже, еліпсоїд інерції, побудований для центра куба, є сферою. Відповідно, будь-яка вісь, що проходить через центр однорідного куба є головною центральною віссю інерції. Щоб знайти момент інерції відповідно осі, що проходить через вершину куба, треба до момента інерції відносно паралельної осі, що проходить через центр куба, додати , де — відстань між осями (за теоремою Гюйгенса-Штейнера). Зрозуміло, що (вісь проходить через вершину і центр куба), а (вісь перпендикулярна осі, що дає ). Враховуючи, що для однорідного куба будь-який головний момент інерції дорівнює для максимального і мінімального моментів інерції відносно осі, що проходить через вершину, матимемо:

ВІДПОВІДЬ НА ЗАПИТАННЯ 17. 2 При якому співвідношенні між висотою і діаметром однорідного циліндра його момент інерції відносно осі, що проходить через центр мас, не залежатиме від її напрямку? Еліпсоїд інерції для однорідного циліндра, побудований для центра мас, є фігурою обертання відносно осі, що співпадає з віссю циліндра (чому? ). Щоб такий еліпсоїд виродився у сферу (а саме це нам треба за умовою), необхідно так підібрати співвідношення між висотою і діаметром, щоб момент інерції відносно осі циліндра дорівнював моменту інерції відносно осі, яка перпендикулярна першій і проходить через центр мас. Момент інерції відносно осі циліндра добре відомий: Для обчислення другого моменту подумки розіб'ємо циліндр на тонкі диски. Внесок окремого диска до загального моменту інерції буде таким: де — висота циліндра, — відстань від окремого диска до осі, від- носно якої обчислюється момент інерції. Отже, Умова дає

ВІДПОВІДЬ НА ЗАПИТАННЯ 17. 3 При якому куті між віссю кругового однорідного конуса і його твірною еліпсоїд інерції з центром у вершині конуса виродиться у сферу? Z dz r Н z O X Еліпсоїд інерції кругового однорідного конуса з центром у вершині конуса у загальному випадку є фігурою обертання відносно осі, що співпадає з віссю конуса (чому? ). Якщо О — вершина конуса, який розташований відносно системи координат так, як показано на рисунку (OZ співпадає з віссю конуса), то нам треба забезпечити рівність моментів інерції відносно осі OZ і ОХ (будь-якої оcі у площині ХОY). Розглянемо, який внесок до і робить тонкий диск (як складова частина конуса), що розташований на відстані від площини XOY. де — маса диска. Структура виразів дозволяє без інтегрування зробити висновок: щоб забезпечити рівність тобто , треба

ВІДПОВІДЬ НА ЗАПИТАННЯ 17. 4 Яка необхідна і достатня умова того, щоб момент імпульсу тіла, що обертається навколо нерухомої осі, обчислений відносно будь-якої точки на осі обертання, співпадав за напрямком з вектором кутової швидкості? Матриця тензора інерції є матрицею перетворення вектора кутової швидкості у вектор моменту імпульсу ( див. відповідь на завдання 15. 2). Обернемо вісь ОХ 3 системи координат так, щоб вона співпадала за напрямком з ). У цьому випадку означає, що Відповідно, Співпадіння напрямків векторів (тоді і Отже, вісь ОХ 3 є головною віссю інерції для точки О (див. відповідь на завдання 16. 1, де замість ОХ 3 було зручніше використовувати позначення ОZ). У завданні йдеться про обчислення моменту імпульсу відносно будь-якої точки на осі обертання. Це означає, що вісь обертання має бути головною центральною віссю інерції тіла (див. відповідь на завдання 16. 2).
Обертальний_рух_методичка_презентац.ppt