Обернена пропорційність Виконали учні 9 класу Чечелевської ЗОШ 1 -2 ступенів Іванова Тетяна і Барило Ігор
Обернена пропорційність та її властивості Ø Функція, яка задається формулою y =Функція y = k, де x — незалежна змінна, а k — число, яке не дорівнює нулю, називається оберненою пропорційністю. Область визначення цієї функції — множина всіх чисел x, відмінних від нуля. Область значень — множина всіх чисел y, відмінних від нуля. Графіком функції є гіпербола, що має дві вітки, які не з’єднуються між собою і наближаються до осей координат, але не досягають їх. Графік не перетинає вісь ординат. Графік не перетинає вісь абсцис. Якщо число k додатне, то графік функції розміщується в першій і третій координатних чвертях. Функція в цьому випадку є спадною. Якщо число k від’ємне, то графік функції розміщується в другій і четвертій координатних чвертях. Функція в цьому випадку є зростаючою. Графік оберненої пропорційності симетричний відносно початку координат.
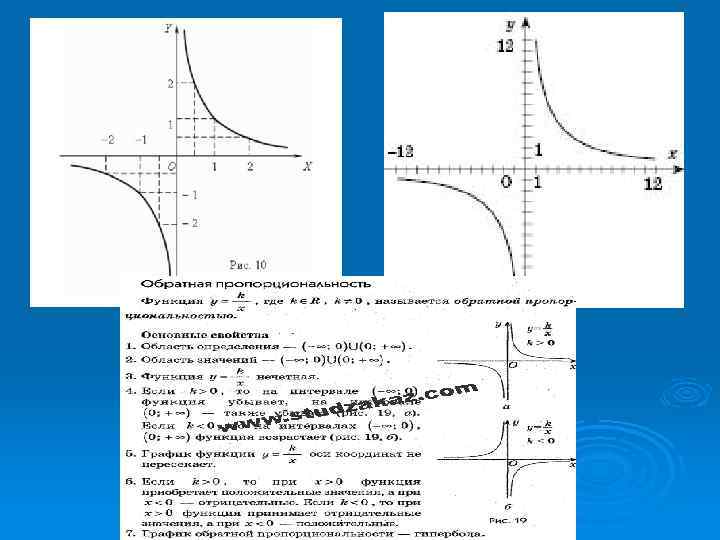
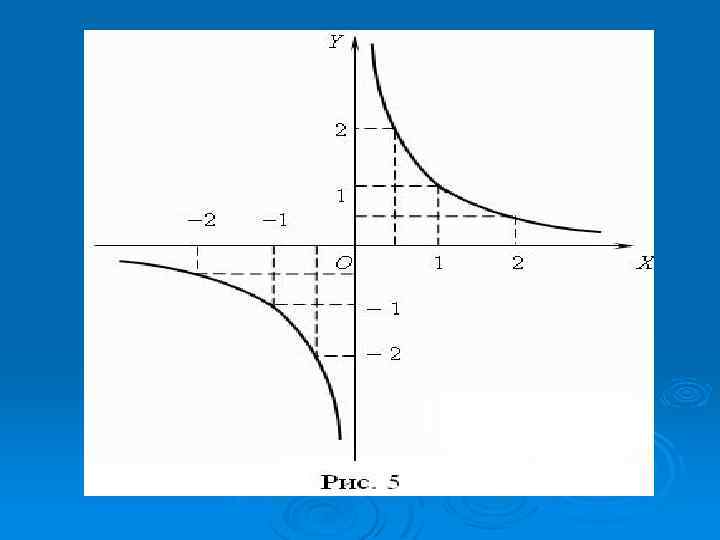
Ø Ø Ø Ø Основні властивості функції 1. , тому що на нуль ділити не можна. 2. , 3. Функція непарна. Замінивши на , отримаємо , тобто . Відмітимо, що графік непарної функції симетричний відносно точки – початку координат. 4. Функція не має нулів, оскільки рівняння не має коренів, графік функції не перетинає вісь . 5. Графік функції називається гіперболою, яка складається з двох віток. Якщо , то вітки гіперболи розташовані в І і ІІІ координатних кутах, і функція є спадною (рис. 5); якщо , то вітки гіперболи розташовані в ІІ і ІV координатних кутах, і функція є зростаючою. Для прикладу оберненої пропорційності, коли , в системі Maple побудуємо графік функції :
Скачать презентацию Обернена пропорційність Виконали учні 9 класу Чечелевської ЗОШ
алгебра.ppt