Объемная TS-диаграмма вод Атлантического океана в 105 км

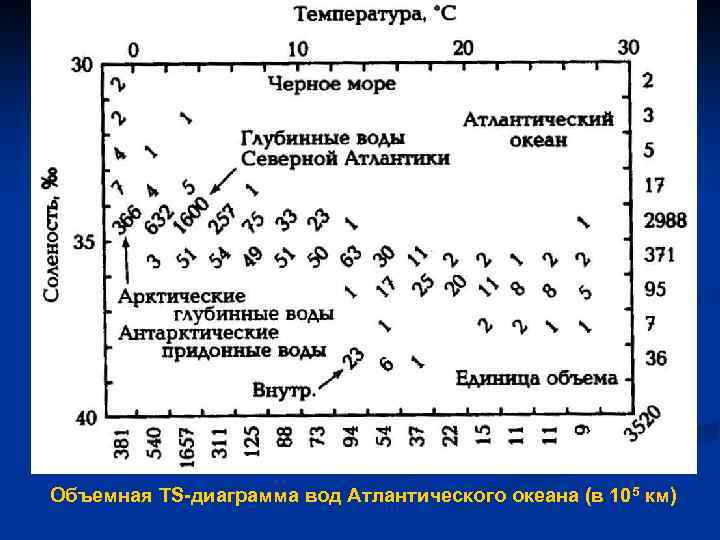
Объемная TS-диаграмма вод Атлантического океана (в 105 км)

Метод резервуаров. Допустим, что океан (или его район) разделен на отдельные части (резервуары, боксы) и каждая секция настолько хорошо перемешана, что ее свойства равномерно распределены по всему объему, и бокс может быть охарактеризован средними значениями этих свойств. Если боксы имеют общие границы, то они обмениваются этими свойствами друг с другом. Задача метода - определить скорость обмена между боксами.

Уравнение баланса параметра внутри бокса

Модель Райта Решением являются переносы: К 1=10. 4 , К 2=1. 6, К 3=1. 0, К 4=7. 1 и К 5=-20. 1.

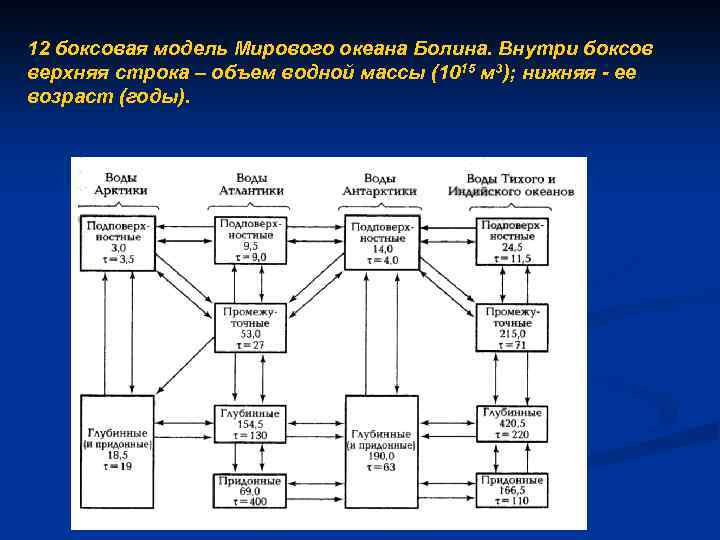
12 боксовая модель Мирового океана Болина. Внутри боксов верхняя строка – объем водной массы (1015 м 3); нижняя - ее возраст (годы).

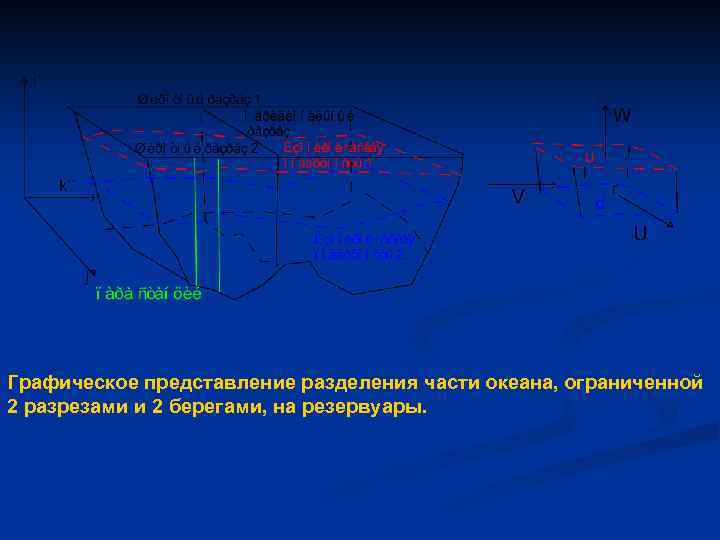
Графическое представление разделения части океана, ограниченной 2 разрезами и 2 берегами, на резервуары.

Уравнения баланса объема для трассера в произвольно выбранном боксе примут вид: al. Vl Cl - ar. Vr Cr+ ad. Wd Cd- au. Wu Cu -al Kl ∂Cl + ar Kr ∂Cr - ad Kd ∂Cd + au Ku ∂Cu ∂y ∂y ∂z ∂z =0 Индексы l, r, u, d обозначают, что величина относится к левой, правой, верхней или нижней грани соответственно, a- площадь соответствующей грани, V и W осредненные по соответствующим граням значения скорости, К - осредненный коэффициент диффузии соответствующего трассера (или теплопроводности, если использована температура). Для данного бокса также верно уравнение неразрывности: al. Vl - ar. Vr + ad. Wd - au. Wu+диффузионные члены = 0

Бокс-моделирование имеет ряд достоинств: • Возможность привлечения дополнительных гидрохимических трассеров, в отличие от динамического метода, где в качестве исходной информации используется только температура и соленость. • Прямое получение осредненных значений абсолютной скорости. • Возможность расчета переносов через изопикнические поверхности, а также диффузионных членов. • Возможность использования математических методов, позволяющих находить ошибки измеренных величин

К недостаткам бокс моделирования относятся: n Проблема адекватности разбиения на боксы реальной структуре океана, а также несоответствие изопикнических поверхностей границам водных масс n Практическое отсутствие информации о граничных условиях (источниках/стоках характеристик) n Неопределенности, связанные с необходимостью введения весовых коэффициентов для различных слоев и характеристик. n Невозможность вычисления изменения со временем концентрации каждого из трассеров в каком-либо боксе. n В большинстве случаев несоответствие количества уравнений и неизвестных, что не позволяет найти единственное решение. n Фактическая минимизация абсолютных значений скоростей.

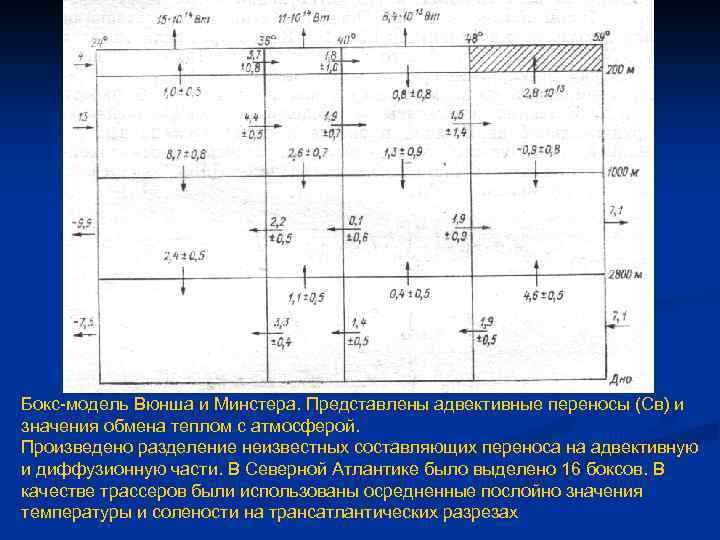
Бокс-модель Вюнша и Минстера. Представлены адвективные переносы (Св) и значения обмена теплом с атмосферой. Произведено разделение неизвестных составляющих переноса на адвективную и диффузионную части. В Северной Атлантике было выделено 16 боксов. В качестве трассеров были использованы осредненные послойно значения температуры и солености на трансатлантических разрезах

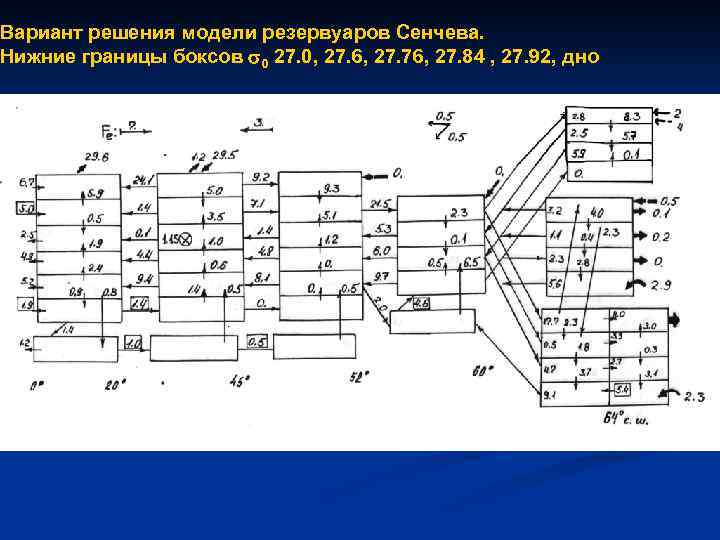
Вариант решения модели резервуаров Сенчева. Нижние границы боксов 0 27. 0, 27. 6, 27. 76, 27. 84 , 27. 92, дно

Расчет процентного содержания водных масс по нескольким параметрам. Система уравнений выглядит следующим образом: S 1 C 1+ S 2 C 2+ S 3 C 3+ S 4 C 4+ S 5 C 5 1 C 1+ 2 C 2+ 3 C 3+ 4 C 4+ 5 C 5 Si 1 C 1+ Si 2 C 2+ Si 3 C 3+ Si 4 C 4+ Si 5 C 5 NO 1 C 1+ NO 2 C 2+ NO 3 C 3+ NO 4 C 4+ NO 5 C 1 + C 2 + C 3 + C 4 + C 5 = S in situ = Si in situ = NO in situ =1 где S – соленость, - потенциальная температура, Si – концентрация силикатов, С – содержание водной массы в долях единицы, индексы соответствуют 100% «чистой» водной массе: 1 – Термоклинной воде, 2 – Антарктической промежуточной водной массе, 3 – Средиземноморской, 4 – Лабрадорской, 5 – Северо-восточной глубинной, а в правой части стоят известные из наблюдений на данном горизонте значения используемых параметров. Неизвестными в этой системе служат содержания водных масс Сi.

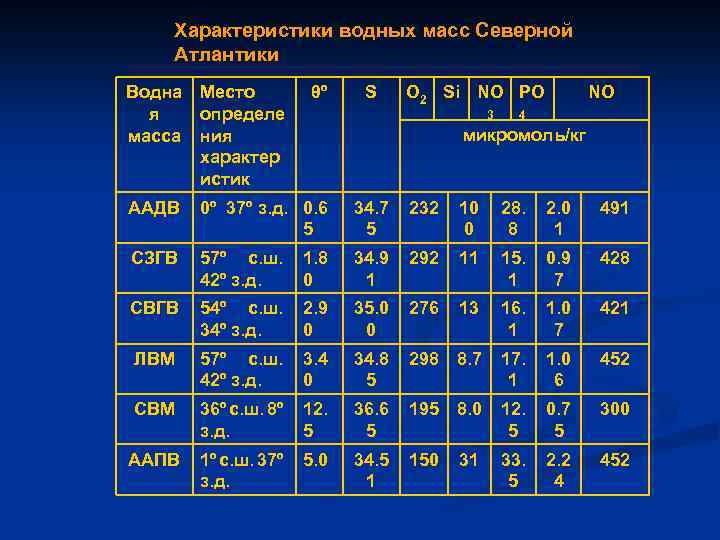
Характеристики водных масс Северной Атлантики Водна Место я определе масса ния характер истик θº S O 2 Si NO PO 3 NO 4 микромоль/кг ААДВ 0º 37º з. д. 0. 6 5 34. 7 5 232 10 0 28. 8 2. 0 1 491 СЗГВ 57º с. ш. 42º з. д. 1. 8 0 34. 9 1 292 11 15. 1 0. 9 7 428 СВГВ 54º с. ш. 34º з. д. 2. 9 0 35. 0 0 276 13 16. 1 1. 0 7 421 ЛВМ 57º с. ш. 42º з. д. 3. 4 0 34. 8 5 298 8. 7 17. 1 1. 0 6 452 СВМ 36º с. ш. 8º з. д. 12. 5 36. 6 5 195 8. 0 12. 5 0. 7 5 300 ААПВ 1º с. ш. 37º з. д. 5. 0 34. 5 1 150 33. 5 2. 2 4 452 31

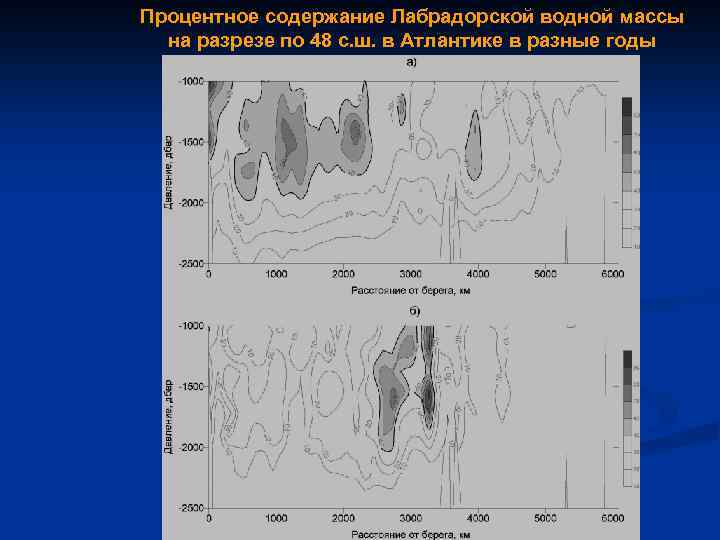
Процентное содержание Лабрадорской водной массы на разрезе по 48 с. ш. в Атлантике в разные годы

Модель Стоммела – Чанади Уравнения переноса массы воды, тепла и соли в T, S-плоскости, соответствующей зональному разрезу в океане, представляются в виде: m(S, T)d. Sd. T = F T m(S, T)d. Sd. T = Н/cp S m(S, T)d. Sd. T = 0, где m(S, T)d. Sd. T - поток массы воды в единичном Т, S - классе с температурой (Т, Т+ Т) и соленостью (S, S+ S), F и Н - потоки пресной воды и тепла в океане, сp -удельная теплоемкость, средняя плотность, положительное направление - на север. Поток массы выражался через меридиональную скорость v(S, T), соответствующую данному T, S-классу площадь зонального разреза а(S, T) и плотность (S, T): m(S, T) = (S, T) a(S, T) v(S, T)

Далее авторы предложили два варианта: 1) Заменить интегралы в системе простыми суммами по трем слоям - верхнему, промежуточному и глубинному, в пределах которых скорость переноса полагается постоянной, а температура и соленость определяются как средневзвешенные значения. Если перейти от потоков массы к объемным расходам Ki, то окончательно система линейных уравнений переноса будет иметь следующий вид: Ki = F Ki. Si =0 Ki. Ti = H/( cp) Система оказывается замкнутой только при рассмотрении трех областей с постоянными значениями скоростей переноса

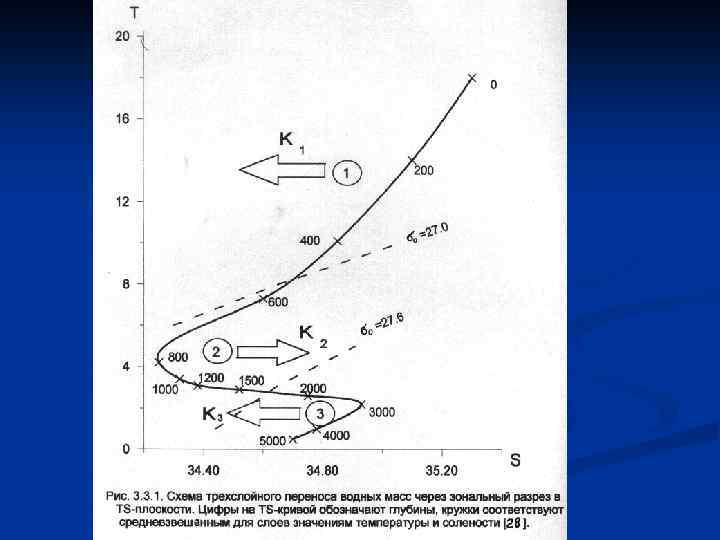
2) Можно также использовать параметрическую зависимость скорости от температуры, считая связь S(T) однозначно заданной из наблюдений. Тогда в системе неизвестными оказываются коэффициенты параболической зависимости v(T): v(T)=b 0+b 1 T 1+b 2 Т 2 (+b 3 T 3)

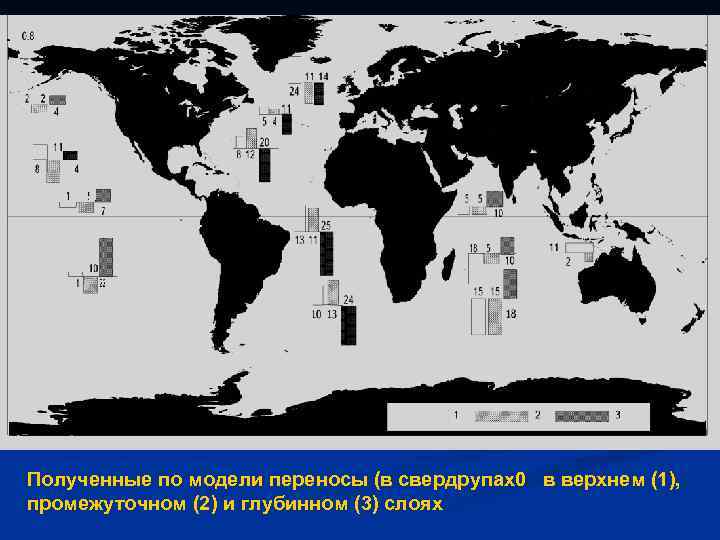
Полученные по модели переносы (в свердрупах0 в верхнем (1), промежуточном (2) и глубинном (3) слоях