OAM Начертательная геометрия Лектор К п н

OAM Начертательная геометрия Лектор К. п. н. , доц. Мусиенко Ольга Алексеевна

Лекция 1 OAM с. 2 Программа обучения студентов МТ на кафедре Начертательной геометрии: 1 семестр – Начертательная геометрия – 18 часов лекций, 36 ч. пр. занятий – зачет; 2 семестр – Инженерная графика – 34 ч. практических занятий – зачет; 3 семестр – Строительное черчение (+Auto. CAD) – 36 ч. практ. зан. – курсовая работа, экзамен (МТб); 4 семестр – 36 ч. лаб. раб. - Компьютерная графика (Auto. CAD) – зачет(МТб)

Лекция 1 OAM Литература: 1. Начертательная геометрия, под ред. Н. Н. Крылова 2. Гордон В. О. и др. Курс начертательной геометрии 3. Короев Ю. И. Начертательная геометрия 4. Гордон В. О. и др. Сборник задач по курсу начертательной геометрии 5. Рабочая тетрадь по начертательной геометрии с. 3

Лекция 1 OAM Формы контроля при обучении НГ: с. 4 1. Проверка задач, самостоятельно выполненных студентом к соответствующему занятию, защита темы. 2. Защита графических работ (5 гр. р. ). 3. 3 аттестации в течение семестра – 100% за своевременное выполнение и защиту графических работ, задач по пройденным темам и рейтинговые контрольные работы, выполненные на 5 баллов. 4. Контрольная работа. 5. Допуск к зачету по выполнению всех выше перечисленных работ. 6. Зачет.

Лекция 1 OAM Начертательная геометрия – это раздел геометрии, в котором изучаются методы изображения пространственных фигур на чертеже и способы решения различных геометрических задач. Основоположником начертательной геометрии считается Госпар Монж (1746 -1818). Его работа «Начертательная геометрия» была напечатана в 1795 г. с. 6

Лекция 1 Мост ч/р Иртыш вблизи г. Тара OAM с. 7

Лекция 1 с. 8 OAM Основные обозначения 1, 2, 3 – плоскости проекций (горизонтальная, фронтальная, А, В, профильная; С – точки в пространстве (объекты проецирования); А 1 , А 2 , А 3 – проекции точки А на плоскости проекций 1, 2, 3; a, b, c – линии в пространстве (прямые и кривые); α, β, γ – плоскости (поверхности) в пространстве. Символы отношений = – совпадение (a=b); // – параллельность (a // b); – перпендикулярность (a b); ∩ – пересечение (a ∩ b= К); – скрещивание (a b); – объединение (Сф Сф); h ( ) – принадлежность (А h b); – касание (α Сф);

Лекция 1 OAM Основной метод начертательной геометрии для получения изображений - метод проекций Проекция - это изображение Проецирование – это процесс Существует 2 метода проецирования: - центральное и параллельное с. 9

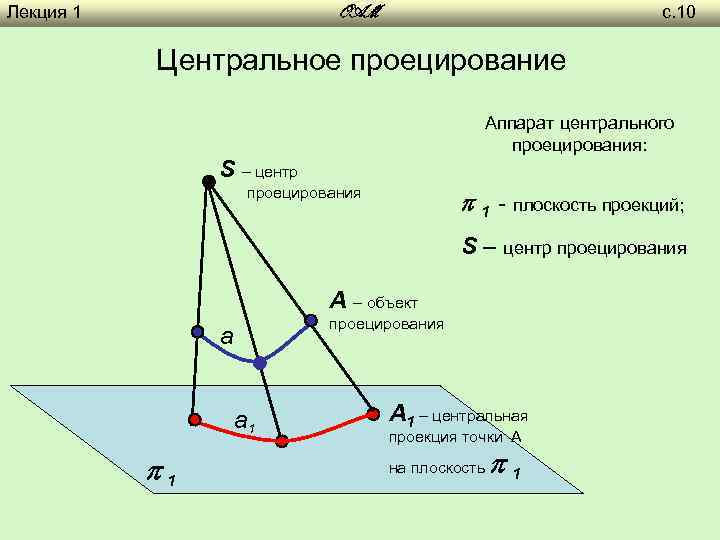Лекция 1 с. 10 OAM Центральное проецирование Аппарат центрального проецирования: S – центр проецирования 1 - плоскость проекций; S – центр проецирования A – объект проецирования a a 1 1 A 1 – центральная проекция точки А на плоскость 1

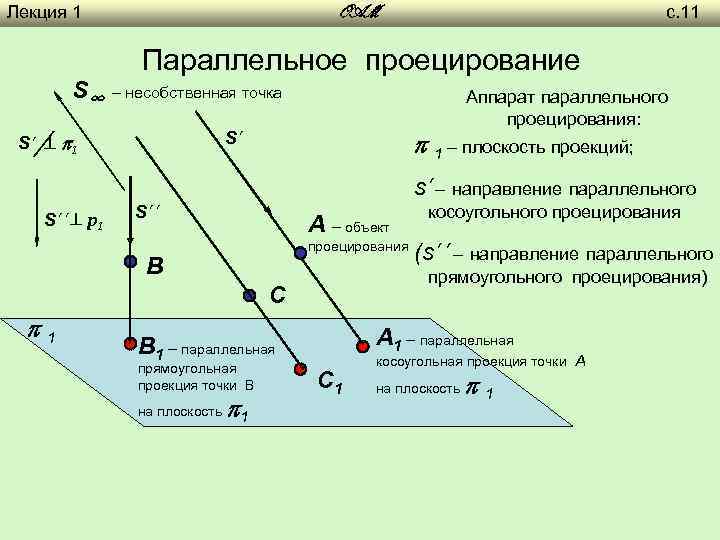Лекция 1 с. 11 OAM Параллельное проецирование S∞ – несобственная точка Аппарат параллельного проецирования: 1 – плоскость проекций; S’ S’ 1 s’– направление параллельного S’’ p 1 S’’ A – объект проецирования B A 1 – параллельная B 1 – параллельная прямоугольная проекция точки B на плоскость 1 (s’’– направление параллельного прямоугольного проецирования) C 1 косоугольного проецирования C 1 косоугольная проекция точки А на плоскость 1

Лекция 1 OAM Ортогональное проецирование точки. Проекционная модель Г. Монжа. с. 12

Лекция 1 OAM Проекционный чертеж должен отвечать требованиям обратимости, то есть возможности реконструировать предмет по чертежу в пространстве с точностью его позиционных и метрических свойств. с. 13

Лекция 1 OAM с. 14 Модель Г. Монжа: 2 ортогональные (т. е. взаимно перпендикулярные) плоскости и система координат. Метод Монжа заключатся в прямоугольном проецировании предметов на две взаимно перпендикулярные плоскости, называемые плоскостями проекций. 1 - горизонтальная плоскость проекций; 2 - фронтальная плоскость проекций.

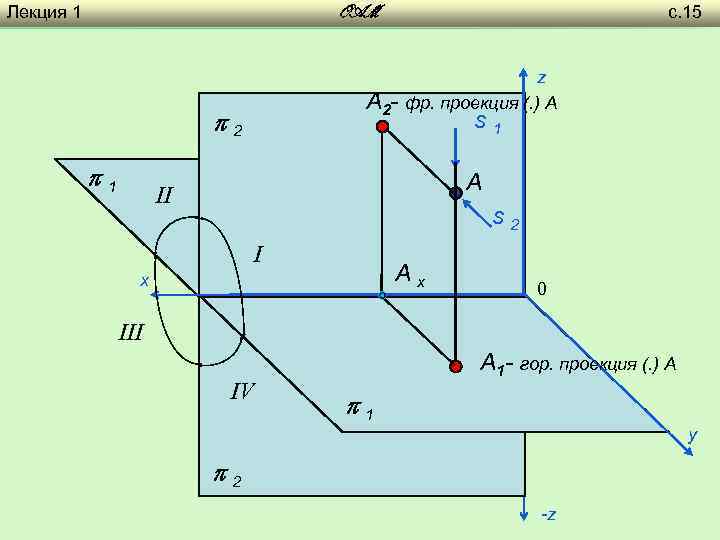Лекция 1 с. 15 OAM z A 2 - фр. проекция (. ) A 2 1 s 1 A II s 2 I Ах х 0 III IV A 1 - гор. проекция (. ) A 1 y 2 -z

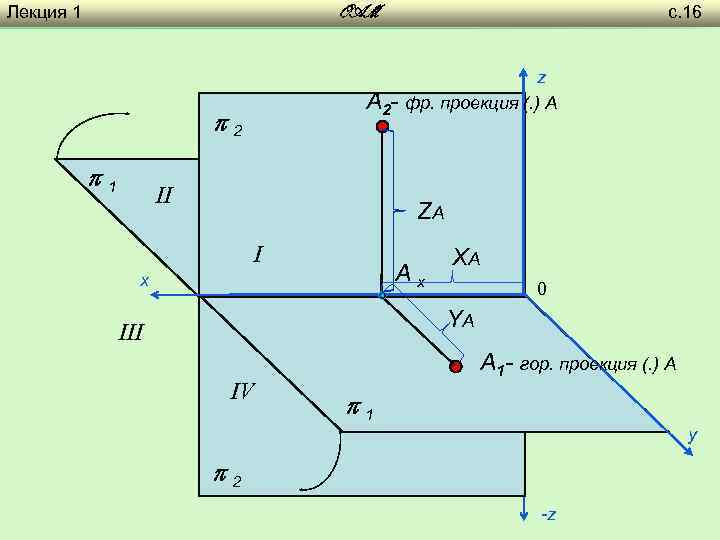Лекция 1 с. 16 OAM z A 2 - фр. проекция (. ) A 2 1 II ZA I Ах х XA 0 YA III IV A 1 - гор. проекция (. ) A 1 y 2 -z

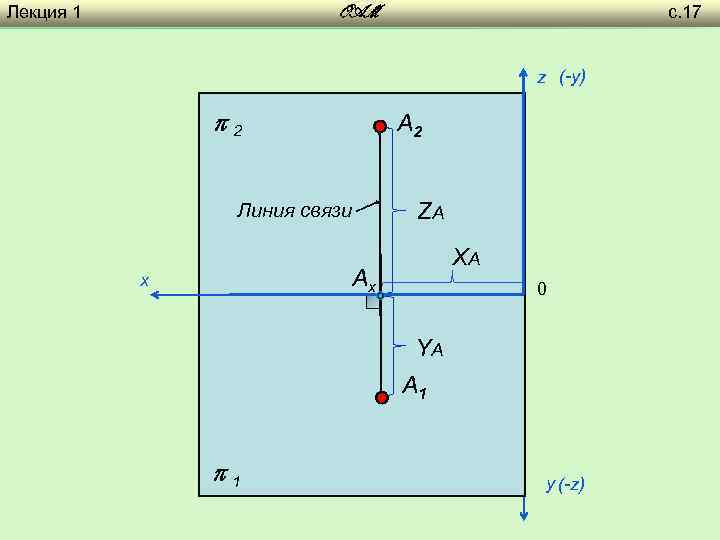Лекция 1 с. 17 OAM z (-y) 2 A 2 ZA Линия связи XA Ах х 0 YA A 1 1 y (-z)

Лекция 1 OAM Проецирование точки на дополнительную плоскость проекций. (Способ замены плоскостей проекций. ) с. 18

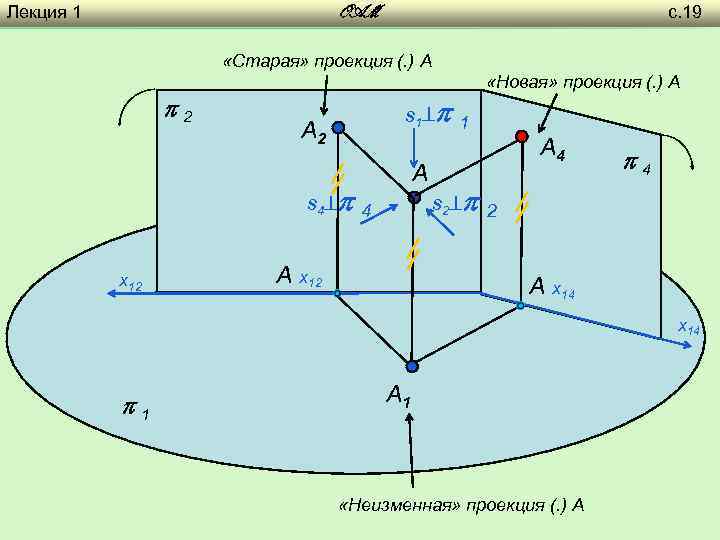Лекция 1 с. 19 OAM «Старая» проекция (. ) A 2 «Новая» проекция (. ) A s 1 1 A 2 A s 4 4 х12 А х12 A 4 4 s 2 2 А х14 1 A 1 «Неизменная» проекция (. ) A

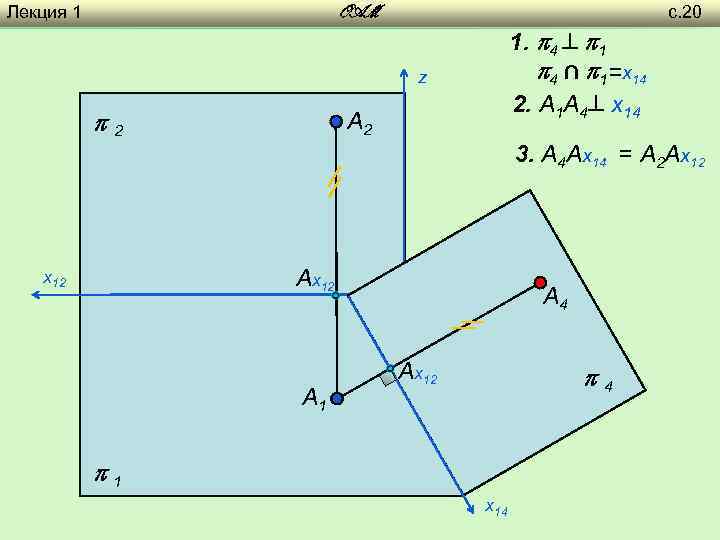Лекция 1 с. 20 OAM 1. 4 1 4 ∩ 1=х14 2. A 1 A 4 х14 z 2 A 2 3. A 4 Ах14 = A 2 Ах12 х12 A 1 A 4 Ах12 4 1 х14

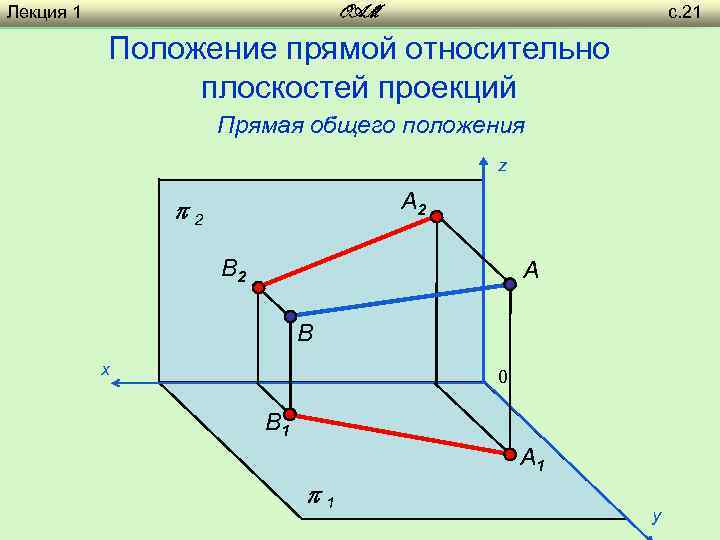Лекция 1 с. 21 OAM Положение прямой относительно плоскостей проекций Прямая общего положения z A 2 2 B 2 A B х 0 B 1 A 1 1 y

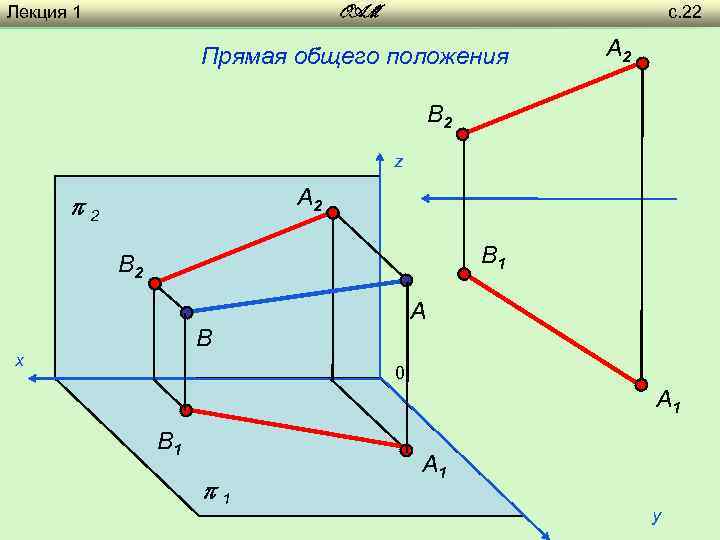Лекция 1 с. 22 OAM Прямая общего положения A 2 B 2 z A 2 2 B 1 B 2 A B х 0 A 1 B 1 1 A 1 y

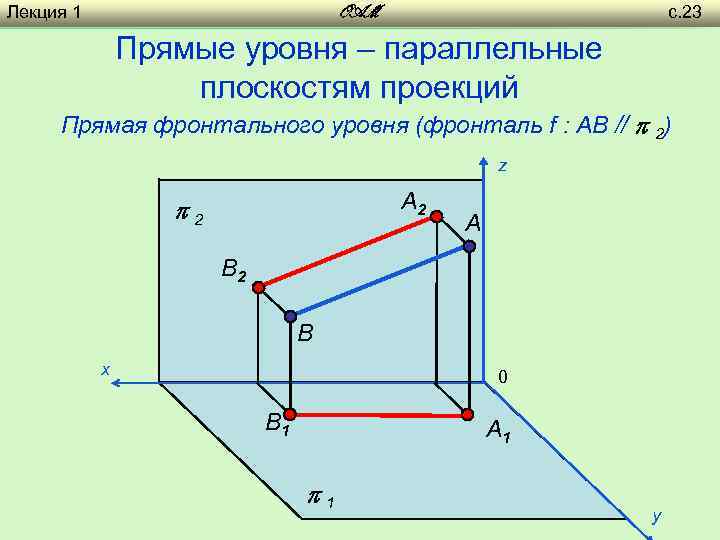Лекция 1 с. 23 OAM Прямые уровня – параллельные плоскостям проекций Прямая фронтального уровня (фронталь f : AB // 2) z A 2 2 A B 2 B х 0 B 1 A 1 1 y

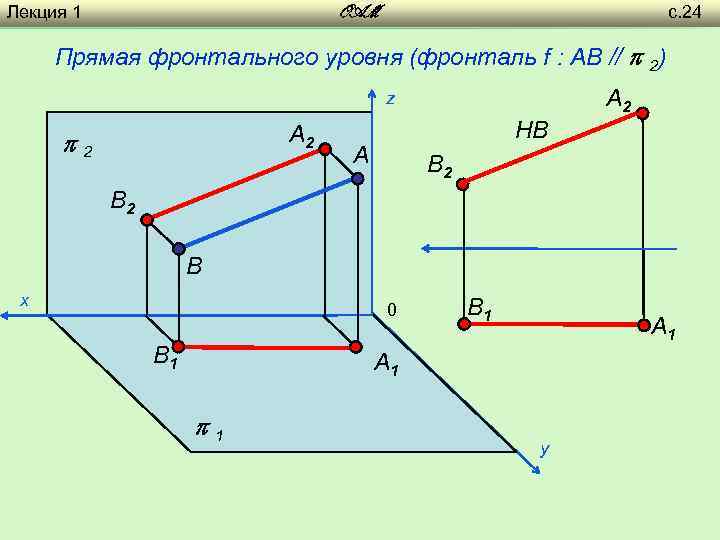Лекция 1 с. 24 OAM Прямая фронтального уровня (фронталь f : AB // 2) A 2 z A 2 2 НВ A B 2 B х 0 B 1 A 1 1 y

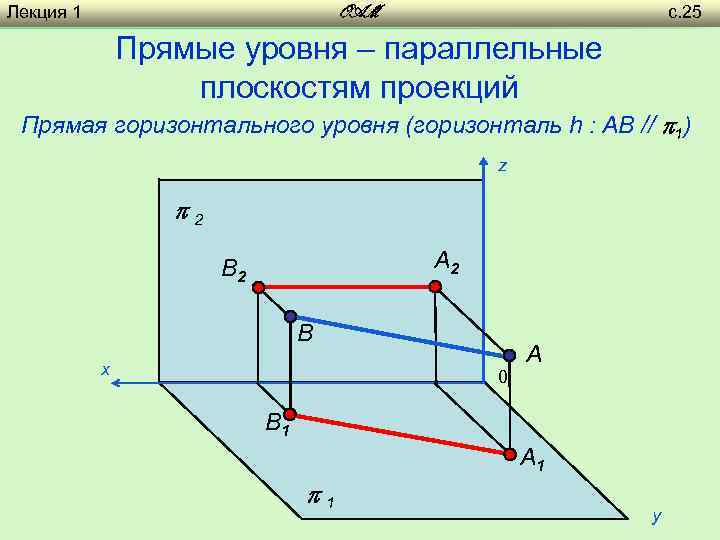Лекция 1 с. 25 OAM Прямые уровня – параллельные плоскостям проекций Прямая горизонтального уровня (горизонталь h : AB // 1) z 2 A 2 B х A 0 B 1 A 1 1 y

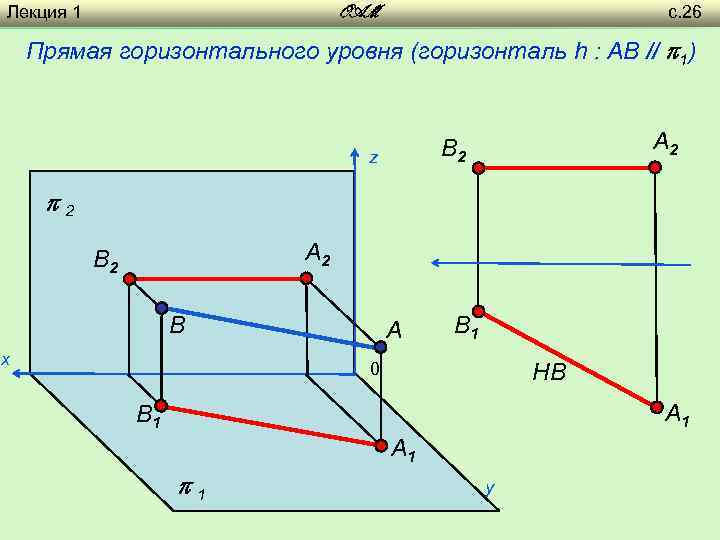Лекция 1 с. 26 OAM Прямая горизонтального уровня (горизонталь h : AB // 1) A 2 B 2 z 2 A 2 B х A B 1 НВ 0 A 1 B 1 A 1 1 y

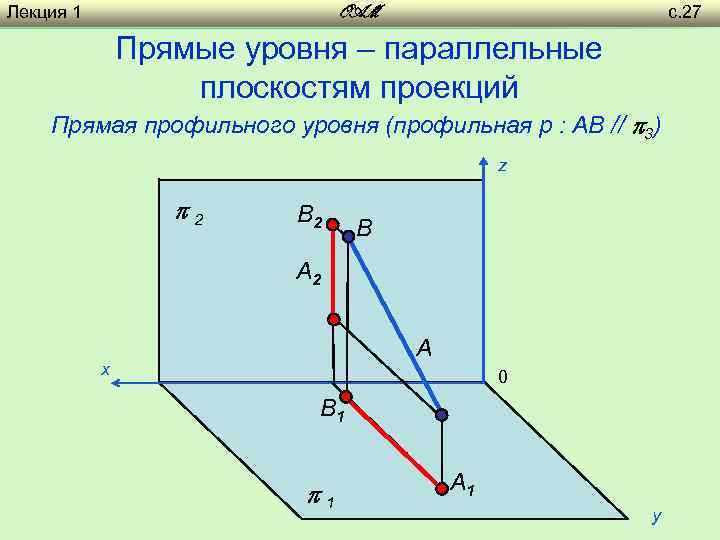Лекция 1 с. 27 OAM Прямые уровня – параллельные плоскостям проекций Прямая профильного уровня (профильная p : AB // 3) z 2 B A 2 A х 0 B 1 1 A 1 y

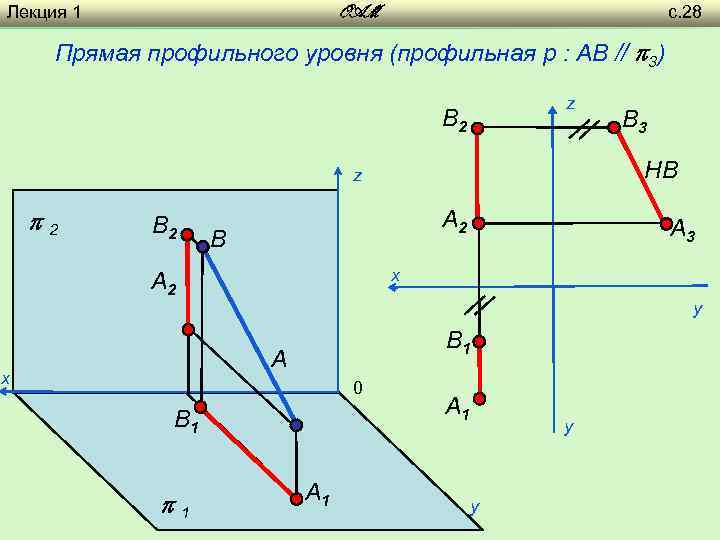Лекция 1 с. 28 OAM Прямая профильного уровня (профильная p : AB // 3) z B 2 НВ z 2 B 2 A 2 B y B 1 A 0 B 1 1 A 3 x A 2 х B 3 A 1 y y

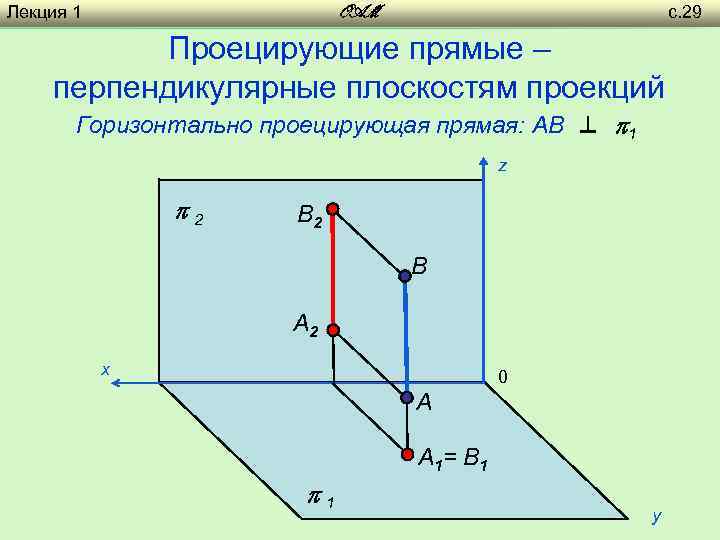Лекция 1 с. 29 OAM Проецирующие прямые – перпендикулярные плоскостям проекций Горизонтально проецирующая прямая: AB ⊥ 1 z 2 B A 2 х 0 A A 1= B 1 1 y

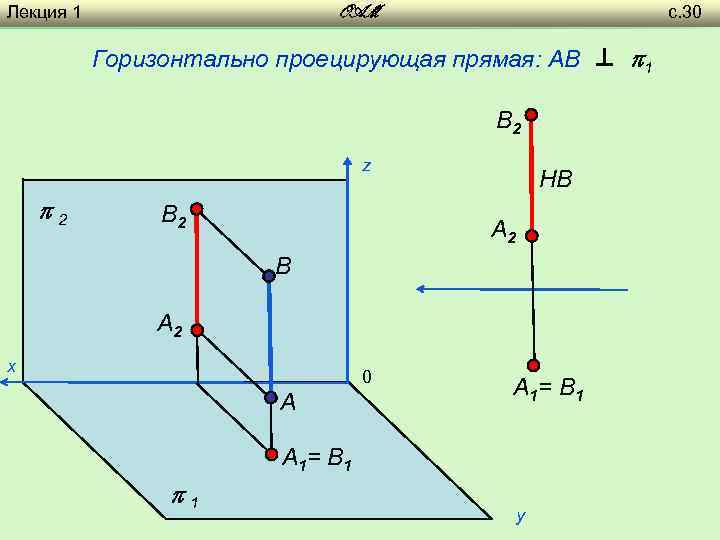Лекция 1 с. 30 OAM Горизонтально проецирующая прямая: AB ⊥ 1 B 2 z 2 B 2 НВ A 2 B A 2 х 0 A A 1= B 1 1 y

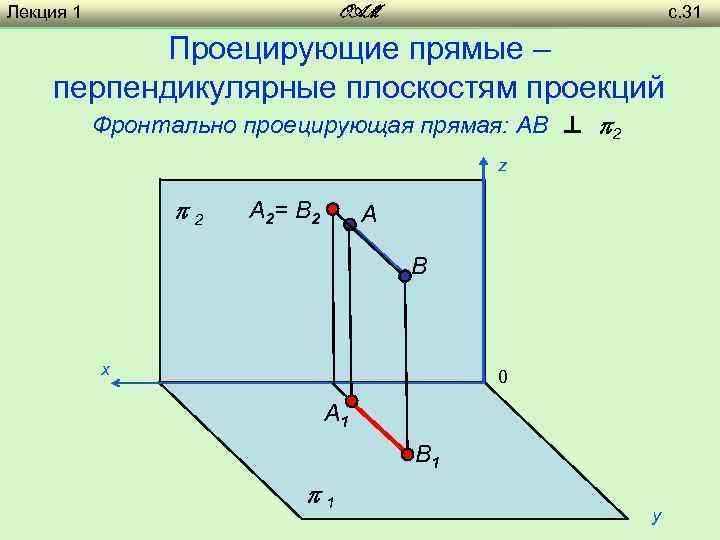Лекция 1 с. 31 OAM Проецирующие прямые – перпендикулярные плоскостям проекций Фронтально проецирующая прямая: AB ⊥ 2 z 2 A 2= B 2 A B х 0 A 1 B 1 1 y

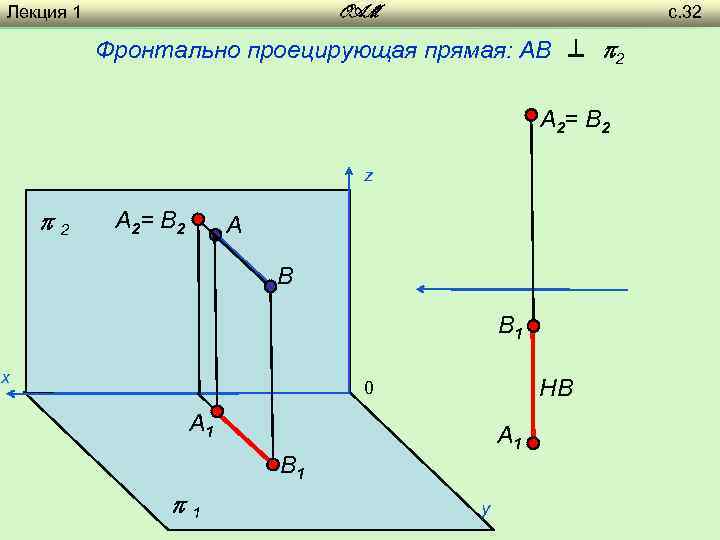Лекция 1 с. 32 OAM Фронтально проецирующая прямая: AB ⊥ 2 A 2= B 2 z 2 A 2= B 2 A B B 1 х НВ 0 A 1 B 1 1 y

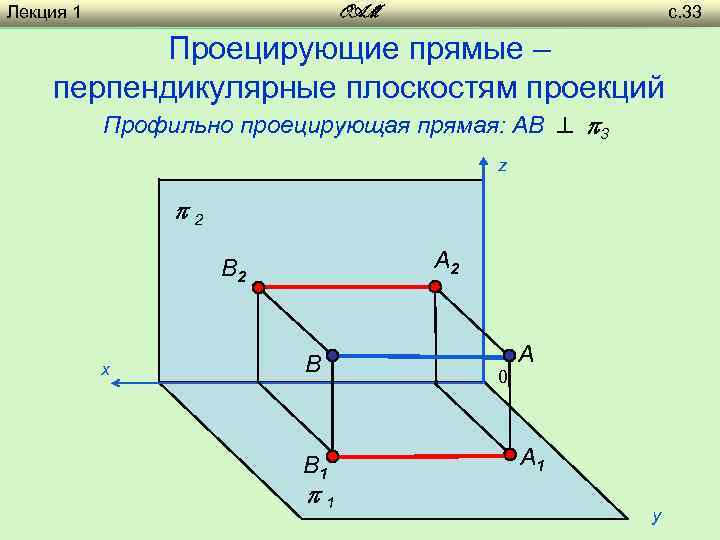Лекция 1 с. 33 OAM Проецирующие прямые – перпендикулярные плоскостям проекций Профильно проецирующая прямая: AB 3 z 2 A 2 B 2 х B B 1 1 A 0 A 1 y

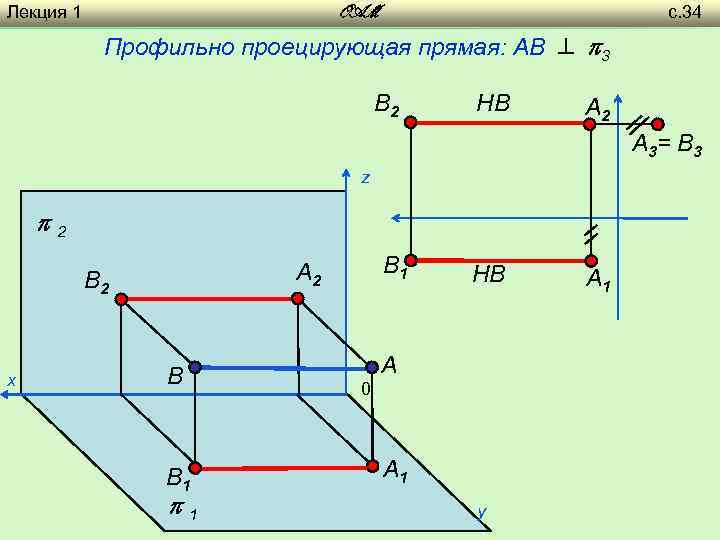Лекция 1 с. 34 OAM Профильно проецирующая прямая: AB 3 B 2 НВ A 2 A 3= B 3 z 2 х B 1 A 2 B B 1 1 НВ A 0 A 1 y A 1

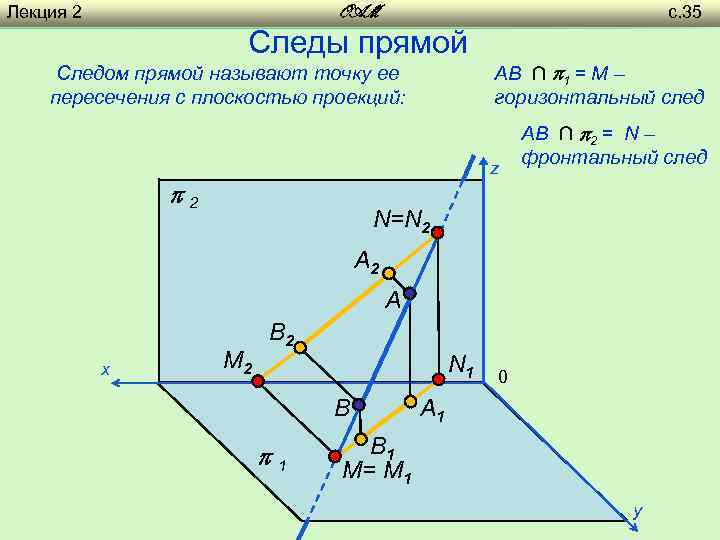Лекция 2 с. 35 OAM Следы прямой Следом прямой называют точку ее пересечения с плоскостью проекций: AB ∩ 1 = М – горизонтальный след z 2 AB ∩ 2 = N – фронтальный след N=N 2 A х М 2 B 2 N 1 B 1 0 A 1 B 1 M= M 1 y

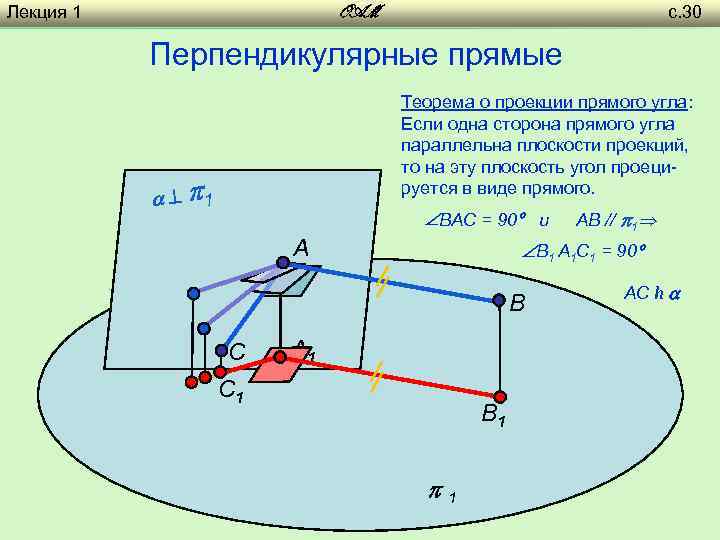Лекция 1 с. 30 OAM Перпендикулярные прямые Теорема о проекции прямого угла: Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость угол проецируется в виде прямого. 1 ВАС = 90 и A В 1 А 1 С 1 = 90 B C АВ // 1 A 1 C 1 B 1 1 АС h

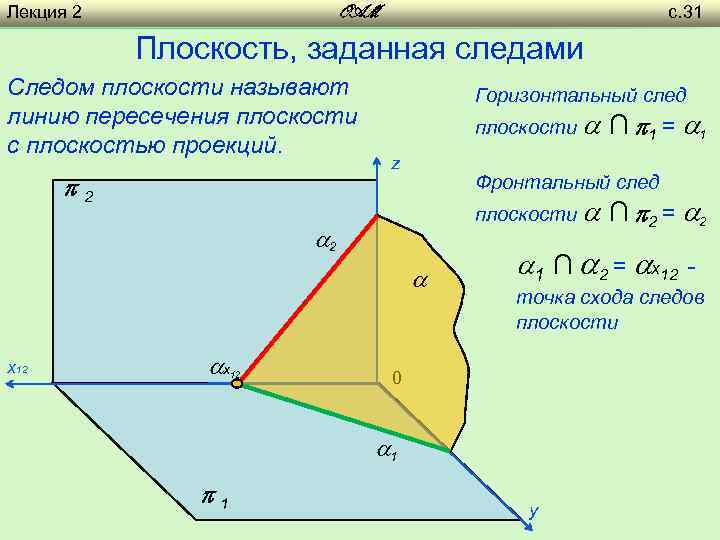Лекция 2 с. 31 OAM Плоскость, заданная следами Следом плоскости называют линию пересечения плоскости с плоскостью проекций. 2 Горизонтальный след плоскости z Фронтальный след плоскости 2 х12 х 12 ∩ 2 = 2 1 ∩ 2 = х12 точка схода следов плоскости 0 1 1 ∩ 1 = 1 y

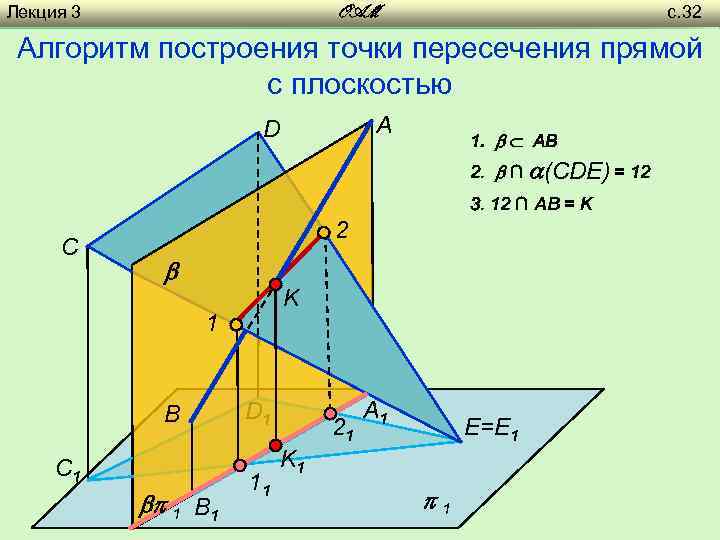Лекция 1 3 с. 32 с. 19 OAM Алгоритм построения точки пересечения прямой с плоскостью A D 1. AB 2. ∩ (CDE) = 12 3. 12 ∩ AB = K C 2 K 1 B C 1 1 B 1 D 1 11 21 A 1 E=E 1 K 1 1

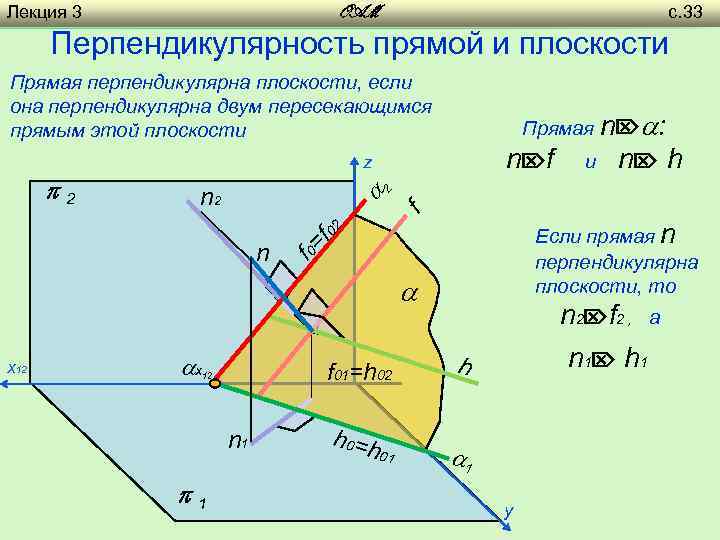Лекция 3 с. 33 OAM Перпендикулярность прямой и плоскости Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости Прямая n : n f z n h n 2 f 2 2 и f 02 f 0= n Если прямая n перпендикулярна плоскости, то х12 х f 01=h 02 12 n 1 1 h 0 =h 01 n 2 f 2 , n 1 h 1 y а

Лекция 4 OAM с. 34 ПОВЕРХНОСТИ Поверхностью называют общую часть двух смежных областей пространства. Поверхностью называют совокупность всех последовательных положений перемещающейся линии. Эту линию называют образующей, а линия, по которой перемещается образующая, называется направляющей.

Лекция 4 OAM с. 35 Многогранники Тетраэдр ? Пирамида Додекаэдр или Октаэдр? Призма

Лекция 1 с. 26 OAM Кривые поверхности F(x, y, z) = 0; z = f(x, y) Поверхность может быть задана: 1) очерком; 2) определителем.

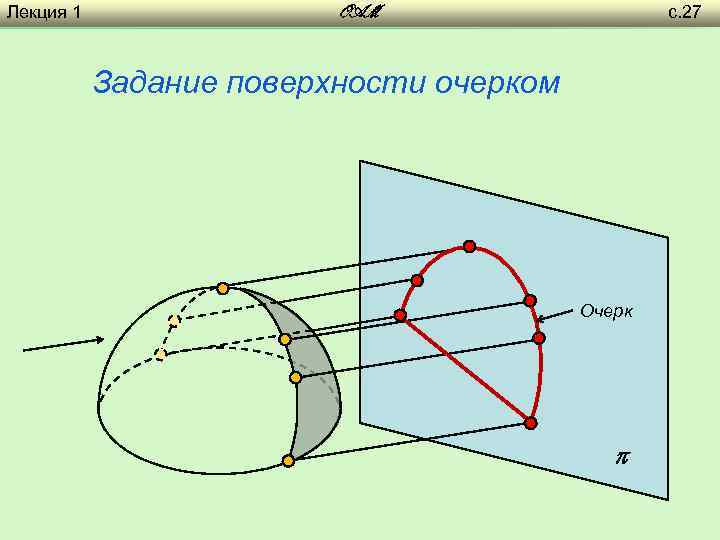Лекция 1 с. 27 OAM Задание поверхности очерком Очерк

Лекция 4 с. 28 OAM Незакономерные поверхности Гауди говорил, что архитекторы придумали прямую линию и симметрию, хотя в природе нет ни того ни другого. Не надо ничего придумывать, надо открывать. Бог уже создал всё. Берцовая кость совершенно неправильна, но держит всё тело. И он всю жизнь строил, пользуясь формой той или иной кости.

Лекция 1 с. 29 OAM Незакономерные поверхности ? Один из странных мостов «Пьяный дом» в Праге

Лекция 1 OAM с. 30 Линейчатые поверхности образуются с помощью движения прямой линии Цилиндрическая поверхность

Лекция 4 Коническая поверхность OAM с. 31

Лекция 4 с. 32 OAM Поверхности с плоскостью параллелизма Коноид

Лекция 4 с. 33 OAM Цилиндроид

Лекция 4 OAM с. 34 Гиперболический параболоид

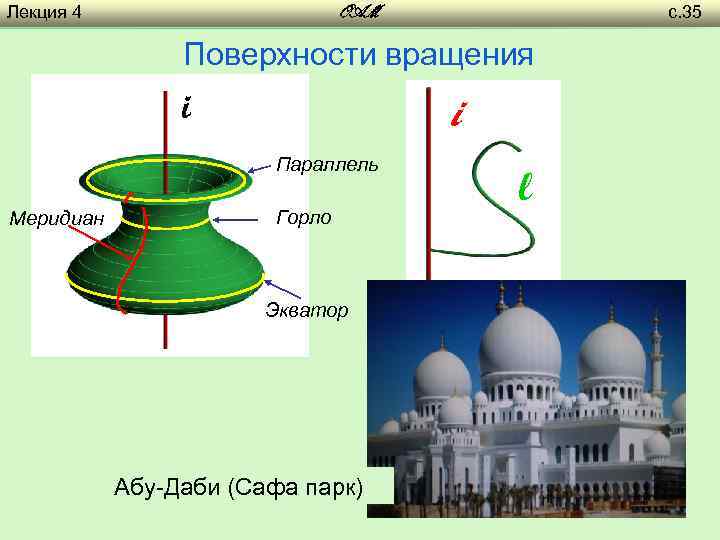Лекция 4 с. 35 OAM Поверхности вращения i i Параллель Меридиан Горло Экватор Абу-Даби (Сафа парк) l

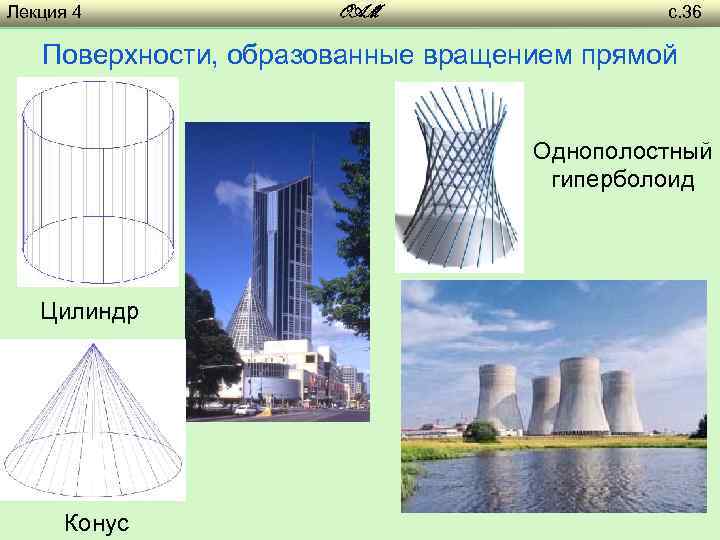Лекция 4 OAM с. 36 Поверхности, образованные вращением прямой Однополостный гиперболоид Цилиндр Конус

Лекция 4 OAM с. 37 Поверхности, образованные вращением окружности Остров-мост в Австрии Сфера

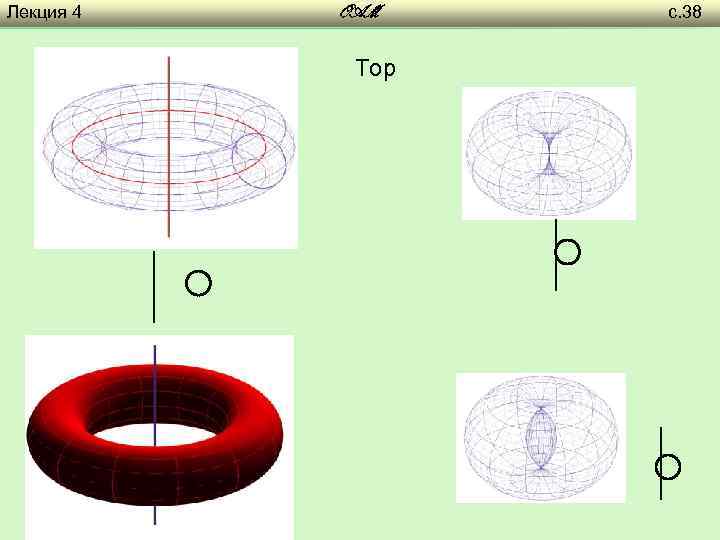Лекция 4 OAM Тор с. 38

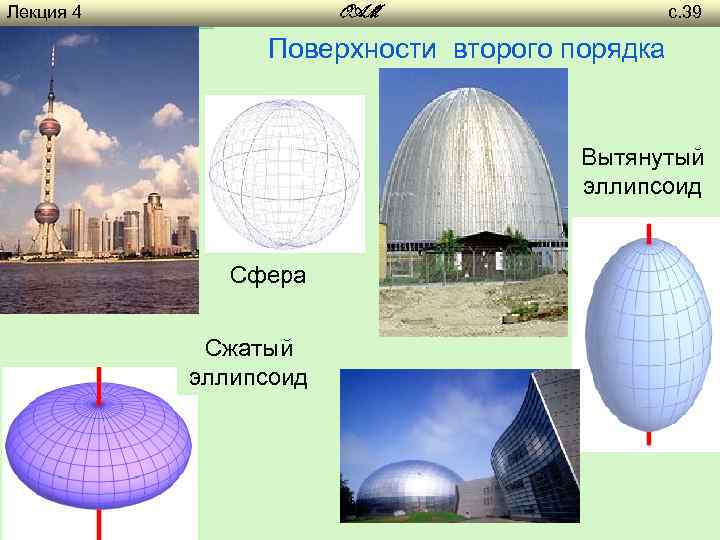Лекция 4 с. 39 OAM Поверхности второго порядка Вытянутый эллипсоид Сфера Сжатый эллипсоид

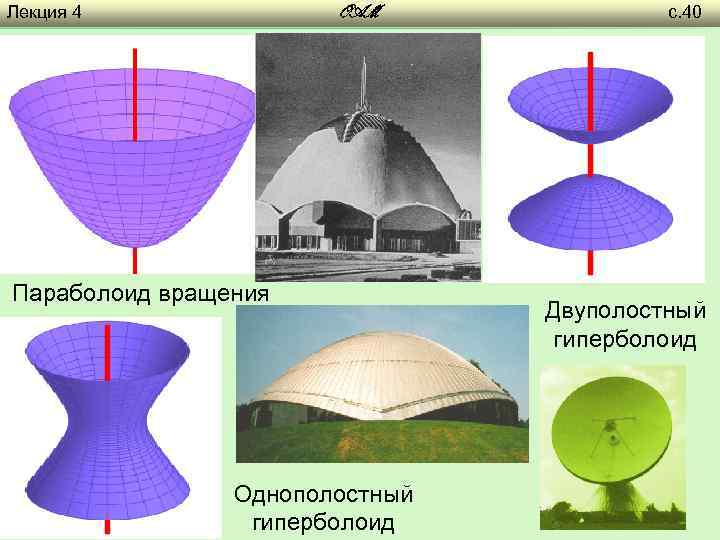Лекция 4 OAM Параболоид вращения Однополостный гиперболоид с. 40 Двуполостный гиперболоид

Лекция 4 OAM с. 41