O log n log n RMRs Randomized Mutual

O(log n / log n) RMRs Randomized Mutual Exclusion Danny Hendler Philipp Woelfel PODC 2009 Ben-Gurion University of Calgary

Distributed Shared Memory (DSM) Model network mem mem mem q n asynchronous fault-free processes, each with its own locally -accessible memory segment. q atomic operations: read / write q local memory accesses: cheap q Remote Memory References (RMR s): expensive

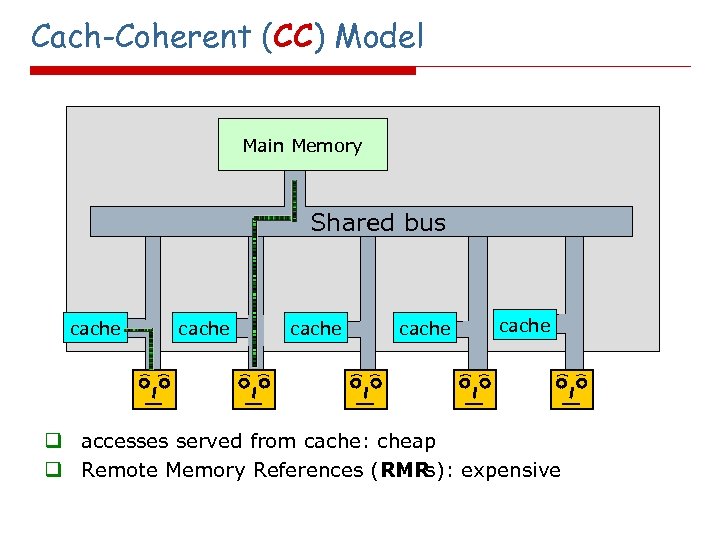Cach-Coherent (CC) Model Main Memory Shared bus cache cache q accesses served from cache: cheap q Remote Memory References (RMR s): expensive

Talk outline q q q q Model Problem statement Prior art and our results Basic Algorithm (CC) Enhanced Algorithm (CC) Pseudo-code Open questions

The mutual exclusion problem (Dijkstra, 1965) We need to devise a protocol that guarantees mutually exclusive access by processes to a shared resource (such as a file, printer, etc. ) Requirements q Mutual exclusion q Starvation freedom Remainder code Entry code Critical Section Exit Section

The RMR metric: motivation Theorem[Alur and Taubenfeld, 92] The winning process in any mutual exclusion algorithm using reads and writes may have to busy-wait for another process q Even the winning process may perform an unbounded number of memory accesses q # of memory accesses not a meaningful metric q Metric used is: worst-case # of RMRs

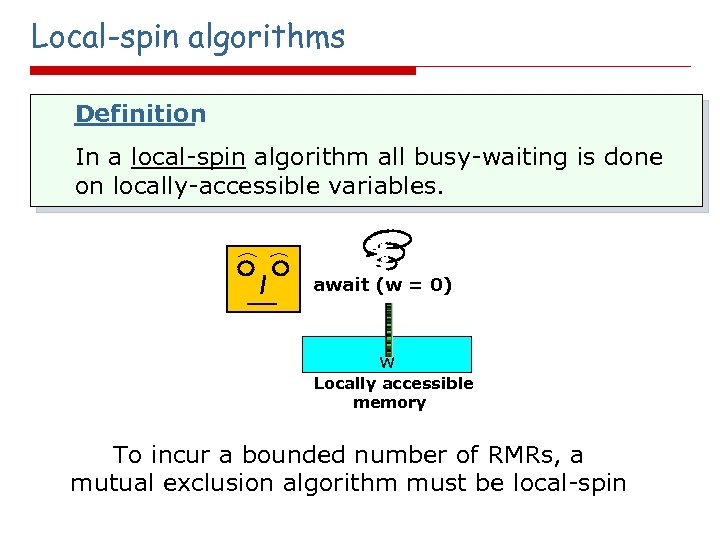Local-spin algorithms Definition In a local-spin algorithm all busy-waiting is done on locally-accessible variables. await (w = 0) w Locally accessible memory To incur a bounded number of RMRs, a mutual exclusion algorithm must be local-spin

Talk outline q q q q Model Problem statement Prior art and our results Basic Algorithm (CC) Enhanced Algorithm (CC) Pseudo-code Open questions

Most Relevant Prior Art q Best upper bound for mutual exclusion: O(log n) RMRs (Yang and Anderson, Distributed Computing '96). q A tight Θ(n log n) RMRs lower bound for deterministic mutex (Attiya, Hendler and Woelfel, STOC '08) q Compare-and-swap (CAS) is equivalent to read/write for RMR complexity (Golab, Hadzilacos, Hendler and Woelfel, PODC '07)

Our Results Randomized mutual exclusion algorithms (for both CC/DSM) that has: q O(log N / log N) expected RMR complexity against a strong adversary, and q O(log N) deterministic worst-case RMR complexity Separation in terms of RMR complexity between deterministic/randomized mutual exclusion algorithms

Shared-memory scheduling adversary types q Oblivious adversary: Makes all scheduling decisions in advance q Weak adversary: Sees a process' coin-flip only after the process takes the following step, can change future scheduling based on history q Strong adversary: Can change future scheduling after each coin-flip / step based on history

Talk outline q q q q Model Problem statement Prior art and our results Basic algorithm (CC model) Enhanced Algorithm (CC model) Pseudo-code Open questions

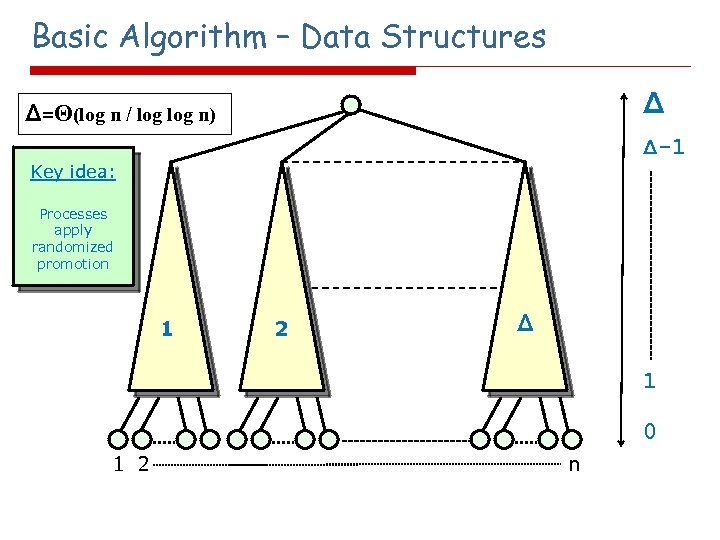Basic Algorithm – Data Structures Δ Δ=Θ(log n / log n) Δ-1 Key idea: Processes apply randomized promotion 1 2 Δ 1 0 1 2 n

Basic Algorithm – Data Structures (cont'd) Promotion Queue pi 1 pi 2 pik notified[1…n] Δ Δ-1 Per-node structure lock {P, } apply: 1 2 Δ 1 12 n 0

Basic Algorithm – Entry Section Δ Δ-1 Lock= i CAS( , i) apply: , i 1 0 i

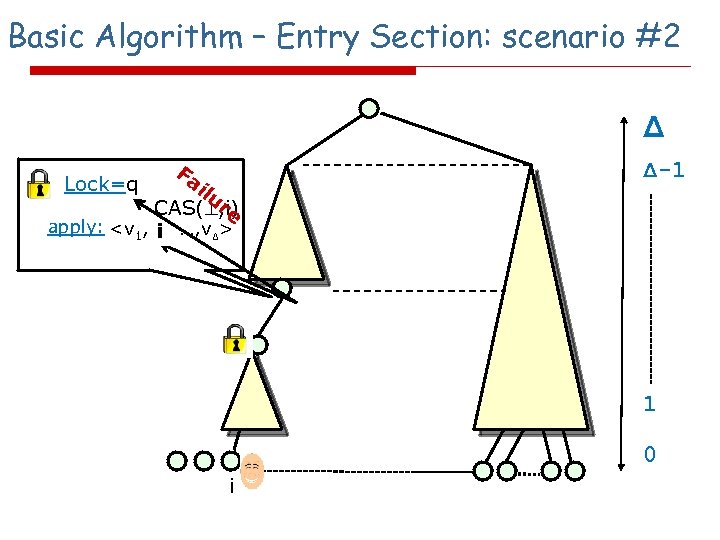Basic Algorithm – Entry Section: scenario #2 Δ Lock=q Fa i lu re CAS( , i) apply: i Δ-1 1 0 i

Basic Algorithm – Entry Section: scenario #2 Δ Δ-1 Lock=q apply: i await (n. lock= ) || apply[ch]= ) 1 0 i

Basic Algorithm – Entry Section: scenario #2 Δ Δ-1 Lock=q apply: i await (n. lock= ) || apply[ch]= ) 1 0 i

Basic Algorithm – Entry Section: scenario #2 Δ Δ-1 await (notified[i=true) ) 1 CS 0 i

Basic Algorithm – Exit Section Lock=p Climb up from leaf until lastapply: node captured q, in entry section Δ Δ-1 1 Lottery 0 i

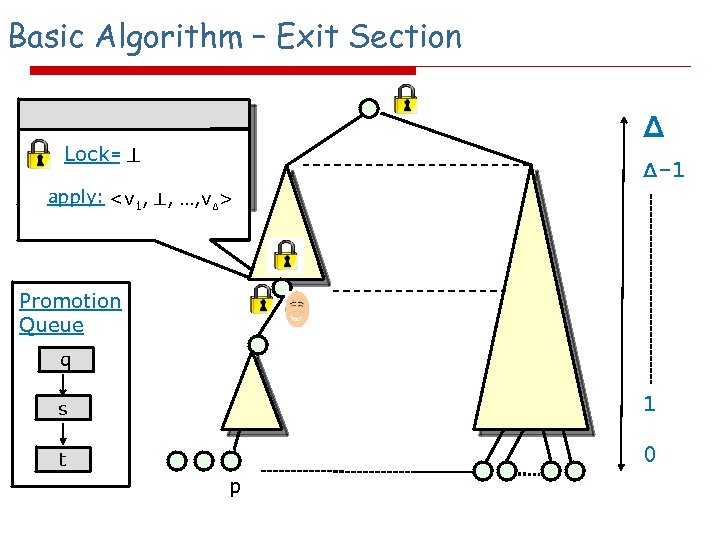Basic Algorithm – Exit Section Δ Perform a lottery Lock=p on the root Δ-1 apply: Promotion Queue q s 1 t 0 p

Basic Algorithm – Exit Section t Δ CS Δ-1 await (notified[i=true) ) Promotion Queue q s 1 t 0 i

Basic Algorithm – Exit Section (scenario #2) Δ Free Root Lock Δ-1 Promotion Queue EMPTY 1 0 i

Basic Algorithm – Properties Lemma: mutual exclusion is satisfied Proof intuition: when a process exits, it either q signals a single process without releasing the root's lock, or q if the promoted-processes queue is empty, releases the lock.

Basic Algorithm – Properties (cont'd) Lemma: Expected RMR complexity is Θ(log N / log N) await (n. lock= ) || apply[ch]= ) A waiting process participates in a lottery every constant number of RMRs incurred here Expected #RMRs incurred before promotion is Θ(log N / log N)

Basic Algorithm – Properties (cont'd) q Mutual Exclusion q Expected RMR complexity: Θ(log N / log N) q Non-optimal worst-case complexity and (even worse) starvation possible.

Talk outline q q q q Model Problem statement Prior art and our results Basic algorithm (CC) Enhanced Algorithm (CC) Pseudo-code Open questions

The enhanced algorithm. Key idea Quit randomized algorithm after incurring ‘'too many’’ RMRS and then execute a deterministic algorithm. Problems q How do we count the number of RMRs incurred? q How do we “quit” the randomized algorithm?

Enhanced algorithm: counting RMRs problem await (n. lock= ) || apply[ch]= ) The problem: A process may incur here an unbounded number of RMRs without being aware of it.

Counting RMRs: solution Key idea Perform both randomized and deterministic promotion Lock=p apply: token: q Increment promotion token whenever releasing a node q Perform deterministic promotion according to promotion index in addition to randomized promotion

The enhanced algorithm: quitting problem Upon exceeding allowed number of RMRs, why can't a process simply release captured locks and revert to a deterministic algorithm? ? 1 2 Δ 12 Waiting processes may incur RMRs without participating in lotteries! N

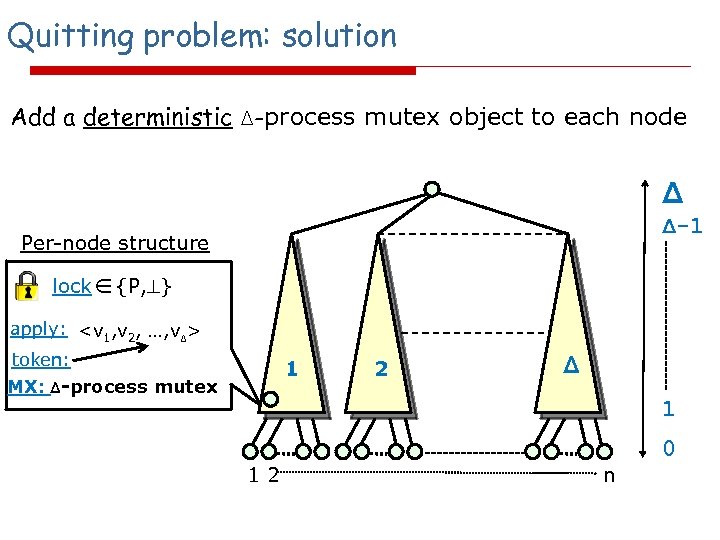Quitting problem: solution Add a deterministic Δ-process mutex object to each node Δ Δ-1 Per-node structure lock {P, } apply: token: 1 MX: Δ-process mutex 2 Δ 1 12 n 0

Quitting problem: solution (cont'd) Per-node structure lock {P, } apply: token: MX: Δ-process mutex • After incurring O(log Δ) RMRs on a node, compete for the MX lock. Then spin trying to capture node lock. • In addition to randomized and deterministic promotion, an exiting process promotes also the process that holds the MX lock, if any.

Quitting problem: solution (cont'd) • After incurring O(log Δ) RMRs on a node, compete for the MX lock. Then spin trying to capture node lock. Worst-case number of RMRs = O(Δ log Δ)=O(log n)

Talk outline q q q q Model Problem statement Prior art and our results Basic algorithm (CC) Enhanced Algorithm (CC) Pseudo-code Open questions

Data-structures the i'th leaf i'th

The entry section i'th

The exit section i'th

Open Problems q Is • • • this best possible? For strong adversary? For weak adversary? For oblivious adversary? q Is there an abortable randomized algorithm? q Is there an adaptive one?

Thanks you! Any questions? 1 2 Δ